- Research Article
- Open access
- Published:
Fast Minimization by Iterative Thresholding for Multidimensional NMR Spectroscopy
Minimization by Iterative Thresholding for Multidimensional NMR Spectroscopy
EURASIP Journal on Advances in Signal Processing volume 2007, Article number: 020248 (2007)
Abstract
Fast multidimensional NMR is important in chemical shift assignment and for studying structures of large proteins. We present the first method which takes advantage of the sparsity of the wavelet representation of the NMR spectra and reconstructs the spectra from partial random measurements of its free induction decay (FID) by solving the following optimization problem: min subject to
subject to , where
, where is a given
is a given observation vector,
observation vector, a random sampling operator,
a random sampling operator, denotes the Fourier transform, and
denotes the Fourier transform, and an orthogonal 2D wavelet transform. The matrix
an orthogonal 2D wavelet transform. The matrix is a given
is a given matrix such that
matrix such that . This problem can be solved by general-purpose solvers; however, these can be prohibitively expensive in large-scale applications. In the settings of interest, the underlying solution is sparse with a few nonzeros. We show here that for large practical systems, a good approximation to the sparsest solution is obtained by iterative thresholding algorithms running much more rapidly than general solvers. We demonstrate the applicability of our approach to fast multidimensional NMR spectroscopy. Our main practical result estimates a four-fold reduction in sampling and experiment time without loss of resolution while maintaining sensitivity for a wide range of existing settings. Our results maintain the quality of the peak list of the reconstructed signal which is the key deliverable used in protein structure determination.
. This problem can be solved by general-purpose solvers; however, these can be prohibitively expensive in large-scale applications. In the settings of interest, the underlying solution is sparse with a few nonzeros. We show here that for large practical systems, a good approximation to the sparsest solution is obtained by iterative thresholding algorithms running much more rapidly than general solvers. We demonstrate the applicability of our approach to fast multidimensional NMR spectroscopy. Our main practical result estimates a four-fold reduction in sampling and experiment time without loss of resolution while maintaining sensitivity for a wide range of existing settings. Our results maintain the quality of the peak list of the reconstructed signal which is the key deliverable used in protein structure determination.
References
Kim S, Szyperski T: GFT NMR, a new approach to rapidly obtain precise high-dimensional NMR spectral information. Journal of the American Chemical Society 2003,125(5):1385-1393. 10.1021/ja028197d
Mobli M, Stern AS, Hoch JC: Spectral reconstruction methods in fast NMR: reduced dimensionality, random sampling and maximum entropy. Journal of Magnetic Resonance 2006,182(1):96-105. 10.1016/j.jmr.2006.06.007
Rovnyak D, Frueh DP, Sastry M, et al.: Accelerated acquisition of high resolution triple-resonance spectra using non-uniform sampling and maximum entropy reconstruction. Journal of Magnetic Resonance 2004,170(1):15-21. 10.1016/j.jmr.2004.05.016
Schmieder P, Stern AS, Wagner G, Hoch JC: Application of nonlinear sampling schemes to COSY-type spectra. Journal of Biomolecular NMR 1993,3(5):569-576.
Schmieder P, Stern AS, Wagner G, Hoch JC: Improved resolution in triple-resonance spectra by nonlinear sampling in the constant-time domain. Journal of Biomolecular NMR 1994,4(4):483-490. 10.1007/BF00156615
Drori I, Cohen-Or D, Yeshurun H: Fragment-based image completion. ACM Transactions on Graphics (TOG) 2003,22(3):303-312. 10.1145/882262.882267
Drori I, Lischinski D: Fast multiresolution image operations in the wavelet domain. IEEE Transactions on Visualization and Computer Graphics 2003,9(3):395-411. 10.1109/TVCG.2003.1207446
Gilbert AC, Guha S, Indyk P, Muthukrishnan S, Strauss M: Near-optimal sparse Fourier representations via sampling. Proceedings on 34th Annual ACM Symposium on Theory of Computing, May 2002, Montreal, Quebec, Canada 152–161.
Donoho DL: Compressed sensing. IEEE Transactions on Information Theory 2006,52(4):1289-1306.
Candès EJ, Romberg J, Tao T: Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Transactions on Information Theory 2006,52(2):489-509.
Berlekamp E, McEliece R, van Tilborg H: On the inherent intractability of certain coding problems. IEEE Transactions on Information Theory 1978,24(3):384-386. 10.1109/TIT.1978.1055873
Chen SS, Donoho DL, Saunders MA: Atomic decomposition by basis pursuit. SIAM Journal of Scientific Computing 1998,20(1):33-61. 10.1137/S1064827596304010
Donoho DL:For most large underdetermined systems of equations, the minimal
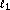 -norm near-solution approximates the sparsest near-solution. Communications on Pure and Applied Mathematics 2006,59(7):907-934. 10.1002/cpa.20131
-norm near-solution approximates the sparsest near-solution. Communications on Pure and Applied Mathematics 2006,59(7):907-934. 10.1002/cpa.20131Efron B, Hastie T, Johnstone I, Tibshirani R: Least angle regression. The Annals of Statistics 2004,32(2):407-499. 10.1214/009053604000000067
Tibshirani R: Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society 1996,58(1):267-288.
Donoho DL, Elad M, Temlyakov VN: Stable recovery of sparse overcomplete representations in the presence of noise. IEEE Transactions on Information Theory 2006,52(1):6-18.
Donoho DL, Huo X: Uncertainty principles and ideal atomic decomposition. IEEE Transactions on Information Theory 2001,47(7):2845-2862. 10.1109/18.959265
Donoho DL, Tsaig Y:Fast solution of
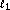 -norm minimization problems when the solution may be sparse. In Tech. Rep. 2006-18. Department of Statistics, Stanford University, Stanford, Calif, USA; 2006.
-norm minimization problems when the solution may be sparse. In Tech. Rep. 2006-18. Department of Statistics, Stanford University, Stanford, Calif, USA; 2006.Saunders MA, Kim B: PDCO: primal-dual interior method for convex objectives. https://doi.org/www.stanford.edu/group/SOL/software/pdco.html
Ye Y: Interior Point Algorithms: Theory and Analysis. John Wiley & Sons, New York, NY, USA; 1997.
Lustig M, Donoho D, Pauly JM: Rapid MR imaging with compressed sensing and randomly under-sampled 3DFT trajectories. Proceedings of the International Society for Magnetic Resonance in Medicine (ISMRM '06), May 2006, Seattle, Wash, USA
Lustig M, Santos JM, Donoho DL, Pauly JM: Rapid MR angiography with randomly under-sampled 3DFT trajectories and non-linear reconstruction. Proceedings of the 9th Annual Scientific Sessions of the Society for Cardiovascular Magnetic Resonance (SCMR '06), January 2006, Miami, Fla, USA
Lustig M, Santos JM, Lee J-H, Donoho DL, Pauly JM: Compressed sensing for rapid MR imaging. Proceedings of the Signal Processing with Adaptative Sparse Structured Representations (SPARS '05), November 2005, Rennes, France
Donoho DL, Logan BF: Signal recovery and the large sieve. SIAM Journal on Applied Mathematics 1992,52(2):577-591. 10.1137/0152031
Candès EJ, Tao T: Decoding by linear programming. IEEE Transactions on Information Theory 2005,51(12):4203-4215. 10.1109/TIT.2005.858979
Rudelson M, Vershynin R: Geometric approach to error-correcting codes and reconstruction of signals. International Mathematics Research Notices 2005, 2005: 4019–4041. 10.1155/IMRN.2005.4019
Drori I, Stodden VC, Hurowitz EH:Fast
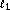 minimization for genome-wide analysis of mRNA lengths. Proceedings of the IEEE International Workshop on Genomic Signal Processing and Statistics (GENSIPS '06), May 2006, College Station, Tex, USA 19–20.
minimization for genome-wide analysis of mRNA lengths. Proceedings of the IEEE International Workshop on Genomic Signal Processing and Statistics (GENSIPS '06), May 2006, College Station, Tex, USA 19–20.Freeman R, Kupče E: New methods for fast multidimensional NMR. Journal of Biomolecular NMR 2003,27(2):101-114. 10.1023/A:1024960302926
Malmodin D, Billeter M: High-throughput analysis of protein NMR spectra. Progress in Nuclear Magnetic Resonance Spectroscopy 2005,46(2-3):109-129. 10.1016/j.pnmrs.2005.01.002
Hoch JC, Stern AS: NMR Data Processing. John Wiley & Sons, New York, NY, USA; 1996.
Hiller S, Fiorito F, Wüthrich K, Wider G: Automated projection spectroscopy (APSY). Proceedings of the National Academy of Sciences of the United States of America 2005,102(31):10876-10881. 10.1073/pnas.0504818102
Kupče E, Freeman R: Fast reconstruction of four-dimensional NMR spectra from plane projections. Journal of Biomolecular NMR 2004,28(4):391-395.
Orekhov VY, Ibraghimov I, Billeter M: Optimizing resolution in multidimensional NMR by three-way decomposition. Journal of Biomolecular NMR 2003,27(2):165-173. 10.1023/A:1024944720653
Donoho DL, Tsaig Y, Drori I, Starck J-L: Sparse solution of underdetermined linear equations by stagewise orthogonal matching pursuit. In Tech. Rep. 2006-02. Department of Statistics, Stanford University, Stanford, Calif, USA; 2006.
Sardy S, Bruce AG, Tseng P: Block coordinate relaxation methods for nonparametric wavelet denoising. Journal of Computational and Graphical Statistics 2000,9(2):361-379. 10.2307/1390659
Sardy S, Bruce AG, Tseng P: Robust wavelet denoising. IEEE Transactions on Signal Processing 2001,49(6):1146-1152. 10.1109/78.923297
Daubechies I, Defrise M, De Mol C: An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Communications on Pure and Applied Mathematics 2004,57(11):1413-1457. 10.1002/cpa.20042
Elad M: Why simple shrinkage is still relevant for redundant representations? IEEE Transactions on Information Theory 2006,52(12):5559-5569.
Elad M, Matalon B, Zibulevsky M: Coordinate and subspace optimization methods for linear least squares with non-quadratic regularization. Journal on Applied and Computational Harmonic Analysis 2006.
Figueiredo MAT, Nowak RD: An EM algorithm for wavelet-based image restoration. IEEE Transactions on Image Processing 2003,12(8):906-916. 10.1109/TIP.2003.814255
Figueiredo MAT, Nowak RD: A bound optimization approach to wavelet-based image deconvolution. Proceedings of the IEEE International Conference on Image Processing (ICIP '05), September 2005, Genova, Italy 2: 782–785.
Paige CC, Saunders MA: LSQR: an algorithm for sparse linear equations and sparse least squares. ACM Transactions on Mathematical Software (TOMS) 1982,8(1):43-71. 10.1145/355984.355989
Pati YC, Rezaiifar R, Krishnaprasad PS: Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition. Proceedings of the 27th Asilomar Conference on Signals, Systems & Computers, November 1993, Pacific Grove, Calif, USA 1: 40–44.
Tropp JA: Greed is good: algorithmic results for sparse approximation. IEEE Transactions on Information Theory 2004,50(10):2231-2242. 10.1109/TIT.2004.834793
Lee PT, Li J, Chapman MR, et al.: SESAME: an experiment management system for biomolecular NMR. https://doi.org/www.sesame.wisc.edu
Daubechies I: Ten Lectures on Wavelets, CBMS-NSF Regional Conference Series in Applied Mathematics. SIAM, Philadelphia, Pa, USA; 1994.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://doi.org/creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Drori, I. Fast Minimization by Iterative Thresholding for Multidimensional NMR Spectroscopy.
EURASIP J. Adv. Signal Process. 2007, 020248 (2007). https://doi.org/10.1155/2007/20248
Minimization by Iterative Thresholding for Multidimensional NMR Spectroscopy.
EURASIP J. Adv. Signal Process. 2007, 020248 (2007). https://doi.org/10.1155/2007/20248
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/20248
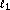 -norm near-solution approximates the sparsest near-solution. Communications on Pure and Applied Mathematics 2006,59(7):907-934. 10.1002/cpa.20131
-norm near-solution approximates the sparsest near-solution. Communications on Pure and Applied Mathematics 2006,59(7):907-934. 10.1002/cpa.20131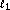 -norm minimization problems when the solution may be sparse. In Tech. Rep. 2006-18. Department of Statistics, Stanford University, Stanford, Calif, USA; 2006.
-norm minimization problems when the solution may be sparse. In Tech. Rep. 2006-18. Department of Statistics, Stanford University, Stanford, Calif, USA; 2006.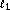 minimization for genome-wide analysis of mRNA lengths. Proceedings of the IEEE International Workshop on Genomic Signal Processing and Statistics (GENSIPS '06), May 2006, College Station, Tex, USA 19–20.
minimization for genome-wide analysis of mRNA lengths. Proceedings of the IEEE International Workshop on Genomic Signal Processing and Statistics (GENSIPS '06), May 2006, College Station, Tex, USA 19–20.