- Research Article
- Open access
- Published:
Modeling of Electric Disturbance Signals Using Damped Sinusoids via Atomic Decompositions and Its Applications
EURASIP Journal on Advances in Signal Processing volume 2007, Article number: 029507 (2007)
Abstract
The number of waveforms monitored in power systems is increasing rapidly. This creates a demand for computational tools that aid in the analysis of the phenomena and also that allow efficient transmission and storage of the information acquired. In this context, signal processing techniques play a fundamental role. This work is a tutorial reviewing the principles and applications of atomic signal modeling of electric disturbance signals. The disturbance signal is modeled using a linear combination of damped sinusoidal components which are closely related to the phenomena typically observed in power systems. The signal model obtained is then employed for disturbance signal denoising, filtering of "DC components," and compression.
References
Rodrigues MAM, de Figueiredo MVF, Miranda ALL, Diniz SS: Oscillography for power system operational planning. Proceedings of the 7th Symposium of Specialists in Electric Operational and Expansion Planning (VII SEPOPE '00), May 2000, Curitiba, Brazil
Arrillaga J, Bollen MHJ, Watson NR: Power quality following deregulation. Proceedings of the IEEE 2000,88(2):246-261. 10.1109/5.824002
Dugan RC, McGranghan MF, Beaty HW: Electrial Power Systems Quality. McGraw-Hill, New York, NY, USA; 1996.
Bollen MHJ: Understanding Power Quality Problems—Voltage Sags and Interruptions. IEEE Press, Piscataway, NJ, USA; 2000.
Ruiz-Reyes N, Vera-Candeas P, Jurado F: Discrimination between transient voltage stability and voltage sag using damped sinusoids-based transient modeling. IEEE Transactions on Power Delivery 2005,20(4):2644-2650. 10.1109/TPWRD.2005.855436
Kezunovic M, Rikalo I: Automating the analysis of faults and power quality. IEEE Computer Applications in Power 1999,12(1):46-50. 10.1109/67.738319
Bujanowski BJ, Pierre JW, Hietpas SM, Sharpe TL, Pierre DA: A comparison of several system identification methods with application to power systems. Proceedings of the 36th Midwest Symposium on Circuits and Systems (MWSCAS '93), August 1993, Detroit, Mich, USA 1: 64–67.
Ibrahim WRA, Morcos MM: Artificial intelligence and advanced mathematical tools for power quality applications: a survey. IEEE Transactions on Power Delivery 2002,17(2):668-673. 10.1109/61.997958
Schweitzer EO III, Hou D: Filtering for protective relays. Proceedings of the 47th Annual Georgia Tech Protective Relaying Conference, April 1993, Atlanta, Ga, USA
Wiot D: A new adaptive transient monitoring scheme for detection of power system events. IEEE Transactions on Power Delivery 2004,19(1):42-48. 10.1109/TPWRD.2003.820416
Lobos T, Rezmer J, Koglin H-J: Analysis of power system transients using wavelets and Prony method. Proceedings of IEEE Porto Power Tech Conference (PTC '01), September 2001, Porto, Portugal 4: 4.
Tawfik MM, Morcos MM: ANN-based techniques for estimating fault location on transmission lines using Prony method. IEEE Transactions on Power Delivery 2001,16(2):219-224. 10.1109/61.915486
Galli AW, Heydt GT, Ribeiro PF: Exploring the power of wavelet analysis. IEEE Computer Applications in Power 1996,9(4):37-41. 10.1109/67.539845
Chung J, Powers EJ, Grady WM, Bhatt SC: Electric power transient disturbance classification using wavelet-based hidden Markov models. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '00), June 2000, Istanbul, Turkey 6: 3662–3665.
Pillaya P, Bhattacharjee A: Application of wavelets to model short-term power system disturbances. IEEE Transactions on Power Systems 1996,11(4):2031-2037. 10.1109/59.544681
Poisson O, Rioual P, Meunier M: Detection and measurement of power quality disturbances using wavelet transform. IEEE Transactions on Power Delivery 2000,15(3):1039-1044. 10.1109/61.871372
Yang H-T, Liao C-C: A de-noising scheme for enhancing wavelet-based power quality monitoring system. IEEE Transactions on Power Delivery 2001,16(3):353-360. 10.1109/61.924810
Santoso S, Grady WM, Powers EJ, Lamoree J, Bhatt SC: Characterization of distribution power quality events with Fourier and wavelet transforms. IEEE Transactions on Power Delivery 2000,15(1):247-254. 10.1109/61.847259
Karimi M, Mokhtari H, Iravani MR: Wavelet based on-line disturbance detection for power quality applications. IEEE Transactions on Power Delivery 2000,15(4):1212-1220. 10.1109/61.891505
Duque CA, Ribeiro MV, Ramos FR, Szczupak J: Power quality event detection based on the divide and conquer principle and innovation concept. IEEE Transactions on Power Delivery 2005,20(4):2361-2369. 10.1109/TPWRD.2005.855478
Ribeiro MV, Romano JMT, Duque CA: An improved method for signal processing and compression in power quality evaluation. IEEE Transactions on Power Delivery 2004,19(2):464-471. 10.1109/TPWRD.2003.822497
Lovisolo L, da Silva EAB, Rodrigues MAM, Diniz PSR: Efficient coherent adaptive representations of monitored electric signals in power systems using damped sinusoids. IEEE Transactions on Signal Processing 2005,53(10 I):3831-3846.
Karimi-Ghartemani M, Iravani MR: A signal processing module for power system applications. IEEE Transactions on Power Delivery 2003,18(4):1118-1126. 10.1109/TPWRD.2003.817514
Mallat S, Zhang Z: Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing 1993,41(12):3397-3415. 10.1109/78.258082
Mallat S: A Wavelet Tour of Signal Processing. 1st edition. Academic Press, San Diego, Calif, USA; 1998.
Ferrando SE, Kolasa LA, Kovačević N: Algorithm 820: a flexible implementation of matching pursuit for Gabor functions on the interval. ACM Transactions on Mathematical Software 2002,28(3):337-353. 10.1145/569147.569151
Goodwin MM, Vetterli M: Matching pursuit and atomic signal models based on recursive filter banks. IEEE Transactions on Signal Processing 1999,47(7):1890-1902. 10.1109/78.771038
Gribonval R, Bacry E: Harmonic decomposition of audio signals with matching pursuit. IEEE Transactions on Signal Processing 2003,51(1):101-111. 10.1109/TSP.2002.806592
Xu W: Component modeling issues for power quality assessment. IEEE Power Engineering Review 2001,21(11):12-15, 17.
Collins JJ, Hurley WG: Application of expert systems and neural networks to the diagnosis of power quality problems. Proceedings of the EPRI-PQA Conference, October 1994, Amsterdam, The Netherlands
Ghosh AK, Lubkeman DL: The classification of power system disturbance waveforms using a neural network approach. IEEE Transactions on Power Delivery 1995,10(1):109-115. 10.1109/61.368408
Lovisolo L, da Silva EAB, Rodrigues MAM, Diniz PSR: Coherent decompositions of power systems signals using damped sinusoids with applications to denoising. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '02), May 2002, Phoenix, Ariz, USA 5: 685–688.
Rodrigues MAM: Efficient decompositions for signal coding, Ph.D. thesis. COPPE/UFRJ, Rio de Janeiro, RJ, USA; 1999.
Friedlander B, Porat B: Detection of transient signals by the Gabor representation. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989,37(2):169-180. 10.1109/29.21680
Friedlander B, Zeira A: Oversampled Gabor representation for transient signals. IEEE Transactions on Signal Processing 1995,43(9):2088-2094. 10.1109/78.414770
Zibulski M, Zeevi YY: Discrete multiwindow Gabor-type transforms. IEEE Transactions on Signal Processing 1997,45(6):1428-1442. 10.1109/78.599955
Kauppinen I, Kauppinen J, Saarinen P: A method for long extrapolation of audio signals. Journal of the Audio Engineering Society 2001,49(12):1167-1180.
Lu Y, Joshi S, Morris JM: Noise reduction for NMR FID signals via Gabor expansion. IEEE Transactions on Biomedical Engineering 1997,44(6):512-528. 10.1109/10.581949
Kay SM: Modern Spectral Estimation. Prentice-Hall, Englewood Cliffs, NJ, USA; 1988.
Tufts DW, Kumaresan R: Improved spectral resolution. Proceedings of the IEEE 1980,68(3):419-421.
Abatzoglou TJ: A fast maximum likelihood algorithm for frequency estimation of a sinusoid based on Newton's method. IEEE Transactions on Acoustics, Speech, and Signal Processing 1985,33(1):77-89. 10.1109/TASSP.1985.1164541
Kumaresan R, Tufts DW: Estimating the parameters of exponentially damped sinusoids and pole-zero modeling in noise. IEEE Transactions on Acoustics, Speech, and Signal Processing 1982,30(6):833-840. 10.1109/TASSP.1982.1163974
Hua Y, Sarkar TK: Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise. IEEE Transactions on Acoustics, Speech, and Signal Processing 1990,38(5):814-824. 10.1109/29.56027
Papadopoulos CK, Nikias CL: Parameter estimation of exponentially damped sinusoids using higher order statistics. IEEE Transactions on Acoustics, Speech, and Signal Processing 1990,38(8):1424-1436. 10.1109/29.57577
Hua Y: Parameter estimation of exponentially damped sinusoids using higher order statistics and matrix pencil. IEEE Transactions on Signal Processing 1991,39(7):1691-1692. 10.1109/78.134411
Ruiz DP, Carrion MC, Gallego A, Medouri A: Parameter estimation of exponentially damped sinusoids using a higher order correlation-based approach. IEEE Transactions on Signal Processing 1995,43(11):2665-2677. 10.1109/78.482116
Ribeiro MV, Park SH, Romano JMT, Mitra SK: A novel MDL-based compression method for power quality applications. IEEE Transactions on Power Delivery 2007,22(1):27-36.
Krim H, Tucker D, Mallat S, Donoho D: On denoising and best signal representation. IEEE Transactions on Information Theory 1999,45(7):2225-2238. 10.1109/18.796365
Vera-Candeas P, Ruiz-Reyes N, Rosa-Zurera M, Martinez-Muñoz D, Lopez-Ferreras F: Transient modeling by matching pursuits with a wavelet dictionary for parametric audio coding. IEEE Signal Processing Letters 2004,11(3):349-352. 10.1109/LSP.2003.822904
Heusdens R, Vafin R, Kleijn WB: Sinusoidal modeling using psychoacoustic-adaptive matching pursuits. IEEE Signal Processing Letters 2002,9(8):262-265. 10.1109/LSP.2002.802999
Jaggi S, Karl WC, Mallat S, Willsky AS: High resolution pursuit for feature extraction. Applied and Computational Harmonic Analysis 1998,5(4):428-449. 10.1006/acha.1997.0239
Goodwin MM: Adaptive Signal Models: Theory, Algorithms, and Audio Applications, Kluwer International Series in Engineering and Computer Science. 1st edition. Kluwer Academic, New York, NY, USA; 1998.
Donoho DL, Vetterli M, DeVore RA, Daubechies I: Data compression and harmonic analysis. IEEE Transactions on Information Theory 1998,44(6):2435-2476. 10.1109/18.720544
Engan K, Aase SO, Husøy JH: Multi-frame compression: theory and design. Signal Processing 2000,80(10):2121-2140. 10.1016/S0165-1684(00)00072-4
Al-Shaykh OK, Miloslavsky E, Nomura T, Neff R, Zakhor A: Video compression using matching pursuits. IEEE Transactions on Circuits and Systems for Video Technology 1999,9(1):123-143. 10.1109/76.744280
Neff R, Zakhor A: Modulus quantization for matching-pursuit video coding. IEEE Transactions on Circuits and Systems for Video Technology 2000,10(6):895-912. 10.1109/76.867927
Caetano R, da Silva EAB, Ciancio AG: Matching pursuits video coding using generalized bit-planes. Proceedings of International Conference on Image Processing (ICIP '02), September 2002, Rochester, NY, USA 3: 677–680.
Gribonval R: From projection pursuit and CART to adaptive discriminant analysis? IEEE Transactions on Neural Networks 2005,16(3):522-532. 10.1109/TNN.2005.844900
Goyal VK, Vetterli M, Thao NT:Quantized overcomplete expansions in
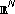 : analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998,44(1):16-31. 10.1109/18.650985
: analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998,44(1):16-31. 10.1109/18.650985Davis G: Adaptive nonlinear approximations, Ph.D. thesis. New York University, New York, NY, USA; 1994.
Tropp JA: Greed is good: algorithmic results for sparse approximation. IEEE Transactions on Information Theory 2004,50(10):2231-2242. 10.1109/TIT.2004.834793
Adler J, Rao BD, Kreutz-Delgado K: Comparison of basis selection methods. Proceedings of the 30th Asilomar Conference on Signals Conference on Signals, Systems & Computers (ACSSC '96), November 1997, Pacific Grove, Calif, USA 1: 252–257.
Zhang Z: Matching pursuits, Ph.D. dissertation. New York University, New York, NY, USA, 1993
Kruskal JB: Toward a practical method to hel uncover the structure of a set of multivariate observations by finding the linear transformation which optimizes a new "index of condensation". In Statistical Computation. Edited by: Milton RC, Nelder JA. Academic Press, New York, NY, USA; 1969.
Friedman JH, Suetzle W: Projection pursuit regression. Journal of the American Statiscal Association 1981,76(376):817-823. 10.2307/2287576
Chen S, Billings SA, Luo W: Orthogonal least squares methods and their application to non-linear system identification. International Journal of Control 1989,50(5):1873-1896. 10.1080/00207178908953472
DeVore RA: Nonlinear approximation. Acta Numerica 1998, 7: 51–150.
Temlyakov VN: Nonlinear methods of approximation. Foundations of Computational Mathematics 2003,3(1):33-107. 10.1007/s102080010029
DeVore RA, Temlyakov VN: Some remarks on greedy algorithms. Advances in Computational Mathematics 1996,5(1):173-187. 10.1007/BF02124742
Gribonval R, Bacry E, Mallat S, Depalle P, Rodet X: Analysis of sound signals with high resolution matching pursuit. Proceedings of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis (TFTSA '96), June 1996, Paris, France 125–128.
Frossard P, Vandergheynst P, Figueras I Ventura RM, Kunt M: A posteriori quantization of progressive matching pursuit streams. IEEE Transactions on Signal Processing 2004,52(2):525-535. 10.1109/TSP.2003.821105
Durka PJ, Ircha D, Blinowska KJ: Stochastic time-frequency dictionaries for matching pursuit. IEEE Transactions on Signal Processing 2001,49(3):507-510. 10.1109/78.905866
Papandreou-Suppappola A, Suppappola SB: Analysis and classification of time-varying signals with multiple time-frequency structures. IEEE Signal Processing Letters 2002,9(3):92-95. 10.1109/97.995826
Ferrando SE, Doolittle EJ, Bernal AJ, Bernal LJ: Probabilistic matching pursuit with Gabor dictionaries. Signal Processing 2000,80(10):2099-2120. 10.1016/S0165-1684(00)00071-2
Daubechies I: Ten Lectures on Wavelets. SIAM, Philadelphia, Pa, USA; 1991.
Etemoǧlu CO, Cuperman V: Matching pursuits sinusoidal speech coding. IEEE Transactions on Speech and Audio Processing 2003,11(5):413-424. 10.1109/TSA.2003.815520
IEEE PES Working Group 1433 Power Quality https://doi.org/grouper.ieee.org/groups/1433/
Cerqueira AS, Duque CA, Trindade RM, Ribeiro MV: Digital system for detection and classification of electrical events. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '05), May 2005, Kobe, Japan 6: 5417–5420.
Canadian-American EMTP User Group : EMTP Rule Book, Alternative Transients Rule Book . Canadian-American EMTP User Group, 1987–1992
Ortega A, Ramchandran K: Rate-distortion methods for: image and video compression. IEEE Signal Processing Magazine 1998,15(6):23-50. 10.1109/79.733495
Tcheou MP, Lovisolo L, da Silva EAB, Rodrigues MAM, Diniz PSR: Optimum rate-distortion dictionary selection for compression of atomic decompositions of electric disturbance signals. IEEE Signal Processing Letters 2007,14(2):81-84.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://doi.org/creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lovisolo, L., Tcheou, M.P., da Silva, E.A.B. et al. Modeling of Electric Disturbance Signals Using Damped Sinusoids via Atomic Decompositions and Its Applications. EURASIP J. Adv. Signal Process. 2007, 029507 (2007). https://doi.org/10.1155/2007/29507
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/29507
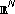 : analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998,44(1):16-31. 10.1109/18.650985
: analysis, synthesis, and algorithms. IEEE Transactions on Information Theory 1998,44(1):16-31. 10.1109/18.650985