- Research Article
- Open access
- Published:
Combined Source-Channel Coding of Images under Power and Bandwidth Constraints
EURASIP Journal on Advances in Signal Processing volume 2007, Article number: 049172 (2006)
Abstract
This paper proposes a framework for combined source-channel coding for a power and bandwidth constrained noisy channel. The framework is applied to progressive image transmission using constant envelope -ary phase shift key (
-ary phase shift key ( -PSK) signaling over an additive white Gaussian noise channel. First, the framework is developed for uncoded
-PSK) signaling over an additive white Gaussian noise channel. First, the framework is developed for uncoded -PSK signaling (with
-PSK signaling (with ). Then, it is extended to include coded
). Then, it is extended to include coded -PSK modulation using trellis coded modulation (TCM). An adaptive TCM system is also presented. Simulation results show that, depending on the constellation size, coded
-PSK modulation using trellis coded modulation (TCM). An adaptive TCM system is also presented. Simulation results show that, depending on the constellation size, coded -PSK signaling performs 3.1 to 5.2 dB better than uncoded
-PSK signaling performs 3.1 to 5.2 dB better than uncoded -PSK signaling. Finally, the performance of our combined source-channel coding scheme is investigated from the channel capacity point of view. Our framework is further extended to include powerful channel codes like turbo and low-density parity-check (LDPC) codes. With these powerful codes, our proposed scheme performs about one dB away from the capacity-achieving SNR value of the QPSK channel.
-PSK signaling. Finally, the performance of our combined source-channel coding scheme is investigated from the channel capacity point of view. Our framework is further extended to include powerful channel codes like turbo and low-density parity-check (LDPC) codes. With these powerful codes, our proposed scheme performs about one dB away from the capacity-achieving SNR value of the QPSK channel.
References
Shannon C: A mathematical theory of communication. The Bell System Technical Journal 1948, 27: 379–423.
Hochwald B, Zeger K: Tradeoff between source and channel coding. IEEE Transactions on Information Theory 1997,43(5):1412–1424. 10.1109/18.623141
Sherwood G, Zeger K: Progressive image coding for noisy channels. IEEE Signal Processing Letters 1997,4(7):189–191. 10.1109/97.596882
Said A, Pearlman W: A new, fast, and efficient image codec based on set partitioning in hierarchical trees. IEEE Transactions on Circuits and Systems for Video Technology 1996,3(3):243–250.
Ramabadran T, Gaitonde S: A tutorial on CRC computations. IEEE Micro 1988,8(4):62–75. 10.1109/40.7773
Hamzaoui R, Stankovic V, Xiong Z: Optimized error protection of scalable image bitstreams. IEEE Signal Processing Magazine 2005,22(6):91–107.
Fossorier M, Xiong Z, Zeger K: Progressive source coding for a power constrained Gaussian channel. IEEE Transactions on Communications 2001,49(8):1301–1306. 10.1109/26.939838
Chande V, Farvardin N: Progressive transmission of images over memoryless noisy channels. IEEE Journal on Selected Areas in Communications 2000,18(6):850–860. 10.1109/49.848239
Farshchian M, Cho S, Pearlman W: Optimal error protection for real-time image and video transmission. IEEE Signal Processing Letters 2004,11(10):780–783. 10.1109/LSP.2004.835470
Ungerboeck G: Channel coding with multilevel/phase signals. IEEE Transactions on Information Theory 1982,28(1):55–67. 10.1109/TIT.1982.1056454
Biglieri E, Divsalar D, McLane P, Simon M: Introduction to Trellis-Coded Modulation with Applications. Macmillan, New York, NY, USA; 1991.
Viterbi A, Wolf J, Zehavi E, Padovani R: A pragmatic approach to trellis-coded modulation. IEEE Communications Magazine 1989,27(7):11–99. 10.1109/35.31452
Wolf J, Zehavi E:
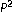 codes: pragmatic trellis codes utilizing punctured convolutional codes. IEEE Communications Magazine 1995,33(2):94–99. 10.1109/35.350381
codes: pragmatic trellis codes utilizing punctured convolutional codes. IEEE Communications Magazine 1995,33(2):94–99. 10.1109/35.350381Kim J, Pottie G: On punctured trellis-coded modulation. IEEE Transactions on Information Theory 1996,42(2):627–636. 10.1109/18.485732
Berrou C, Glavieux A: Near optimum error correcting coding and decoding: turbo-codes. IEEE Transactions on Communications 1996,44(10):1261–1271. 10.1109/26.539767
Gallager R: Low-Density Parity-Check Codes. MIT Press, Cambridge, Mass, USA; 1963.
Shapiro J: Embedded image coding using zerotrees of wavelet coefficients. IEEE Transactions on Signal Processing 1993,41(12):3445–3462. 10.1109/78.258085
Proakis J: Digital Communications. 4th edition. McGraw-Hill, New York, NY, USA; 2001.
Wicker S: Error Control Coding Systems for Digital Communication and Storage. Prentice-Hall, Englewood Cliffs, NJ, USA; 1995.
Pei Y, Modestino J: Multi-layered video transmission over wireless channels using an adaptive modulation and coding scheme. Proceedings of International Conference on Image Processing (ICIP '01), October 2001, Thessaloniki, Greece 1009–1012.
Bahl L, Cocke J, Jelinek F, Raviv J: Optimal decoding of linear codes for minimizing symbol error rate. IEEE Transactions on Information Theory 1974,20(2):284–287.
Fragouli C, Wesel R: Turbo-encoder design for symbol-interleaved parallel concatenated trellis-coded modulation. IEEE Transactions on Communications 2001,49(3):425–435. 10.1109/26.911450
Robertson P, Worz T: Bandwidth-efficient turbo trellis-coded modulation using punctured component codes. IEEE Journals on Selected Areas in Communications 1998,16(2):206–218. 10.1109/49.661109
Goff S, Glavieux A, Berrou C: Turbo-codes and high spectral efficiency modulation. Proceedings of International Conference on Creationism (ICC '94), May 1994, New Orleans, La, USA 3: 1255–1259.
Richardson T, Shokrollahi A, Urbanke R: Design of capacity-approaching irregular low-density parity-check codes. IEEE Transactions on Information Theory 2001,47(1):619–637.
Narayanan K, Altunbas I, Narayanaswami R: Design of codes for minimum shift keying based on density evolution. IEEE Transactions on Communications 2003,51(8):1283–1295. 10.1109/TCOMM.2003.815076
Hou J, Siegel PH, Milstein L, Pfister H: Capacity-approaching bandwidth-efficient coded modulation schemes based on low-density parity-check codes. IEEE Transactions on Information Theory 2003,49(9):2141–2154. 10.1109/TIT.2003.815777
Alouini M, Tang X, Goldsmith A: An adaptive modulation scheme for simultaneous voice and datatransmission over fading channels. IEEE Journal on Selected Areas in Communications 1999,17(5):837–850. 10.1109/49.768199
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://doi.org/creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Raja, N., Xiong, Z. & Fossorier, M. Combined Source-Channel Coding of Images under Power and Bandwidth Constraints. EURASIP J. Adv. Signal Process. 2007, 049172 (2006). https://doi.org/10.1155/2007/49172
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/49172
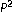 codes: pragmatic trellis codes utilizing punctured convolutional codes. IEEE Communications Magazine 1995,33(2):94–99. 10.1109/35.350381
codes: pragmatic trellis codes utilizing punctured convolutional codes. IEEE Communications Magazine 1995,33(2):94–99. 10.1109/35.350381