- Research Article
- Open access
- Published:
Design of Nonuniform Filter Bank Transceivers for Frequency Selective Channels
EURASIP Journal on Advances in Signal Processing volume 2007, Article number: 061396 (2006)
Abstract
In recent years, there has been considerable interest in the theory and design of filter bank transceivers due to their superior frequency response. In many applications, it is desired to have transceivers that can support multiple services with different incoming data rates and different quality-of-service requirements. To meet these requirements, we can either do resource allocation or design transceivers with a nonuniform bandwidth partition. In this paper, we propose a method for the design of nonuniform filter bank transceivers for frequency selective channels. Both frequency response and signal-to-interference ratio (SIR) can be incorporated in the transceiver design. Moreover, the technique can be extended to the case of nonuniform filter bank transceivers with rational sampling factors. Simulation results show that nonuniform filter bank transceivers with good filter responses as well as high SIR can be obtained by the proposed design method.
References
Van Nee R, Prasad R: OFDM Wireless Multimedia Communication. Artech House, Boston, Mass, USA; 2000.
Luo TH, Liu CH, Phoong S-M, Lin Y-P: Design of channel-resilient DFT bank transceivers. Proceedings of 13th European Signal Processing Conference (EUSIPCO '05), September 2005, Antalya, Turkey
Vetterli M: Perfect transmultiplexers. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '86), April 1986, Tokyo, Japan 11: 2567–2570.
Sandberg SD, Tzannes MA: Overlapped discrete multitone modulation for high speed copper wire communications. IEEE Journal on Selected Areas in Communications 1995,13(9):1571–1585. 10.1109/49.475531
Chen B-S, Tsai C-L, Chen Y-F: Mixed
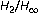 filtering design in multirate transmultiplexer systems: LMI approach. IEEE Transactions on Signal Processing 2001,49(11):2693–2701. 10.1109/78.960416
filtering design in multirate transmultiplexer systems: LMI approach. IEEE Transactions on Signal Processing 2001,49(11):2693–2701. 10.1109/78.960416Martin-Martin P, Cruz-Roldan F, Saramaki T: Optimized transmultiplexers for multirate systems. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '05), May 2005, Kobe, Japan 2: 1106–1109.
Rizos AD, Proakis JG, Nguyen TQ: Comparison of DFT and cosine modulated filter banks in multicarrier modulation. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '94), November–December 1994, San Francisco, Calif, USA 2: 687–691.
Govardhanagiri S, Karp T, Heller P, Nguyen T: Performance analysis of multicarrier modulation systems using cosine modulated filter banks. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '99), March 1999, Phoenix, Ariz, USA 3: 1405–1408.
Ihalainen T, Stitz TH, Renfors M: Efficient per-carrier channel equilier for filter bank based multicarrier systems. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '05), March 2005, Philadelphia, Pa, USA
Phoong S-M, Chang Y, Chen C-Y: DFT-modulated filterbank transceivers for multipath fading channels. IEEE Transactions on Signal Processing 2005,53(1):182–192.
Dasgupta S, Pandharipande A: Optimum multiflow biorthogonal DMT with unequal subchannel assignment. IEEE Transactions on Signal Processing 2005,53(9):3572–3582.
Liu T, Chen T: Design of multichannel nonuniform transmultiplexers using general building blocks. IEEE Transactions on Signal Processing 2001,49(1):91–99. 10.1109/78.890348
Hoang P-Q, Vaidyanathan PP: Non-uniform multirate filter banks: theory and design. Proceedings of IEEE International Symposium on Circuits and Systems, May 1989, Portland, Ore, USA 1: 371–374.
Akkarakaran S, Vaidyanathan PP: New results and open problems on nonuniform filter-banks. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '99), March 1999, Phoenix, Ariz, USA 3: 1501–1504.
Kovacevic J, Vetterli M: Perfect reconstruction filter banks with rational sampling factors. IEEE Transactions on Signal Processing 1993,41(6):2047–2066. 10.1109/78.218135
Princen J: Design of nonuniform modulated filterbanks. IEEE Transactions on Signal Processing 1995,43(11):2550–2560. 10.1109/78.482106
Nayebi K, Barnwell TP III, Smith MJT: Nonuniform filter banks: a reconstruction and design theory. IEEE Transactions on Signal Processing 1993,41(3):1114–1127. 10.1109/78.205717
Argenti F, Brogelli B, Del Re E: Design of pseudo-QMF banks with rational sampling factors using several prototype filters. IEEE Transactions on Signal Processing 1998,46(6):1709–1715. 10.1109/78.678502
Ho CY-F, Ling BW-K, Liu Y-Q, Tam PK-S, Teo K-L: Optimal design of nonuniform FIR transmultiplexer using semi-infinite programming. IEEE Transactions on Signal Processing 2005,53(7):2598–2603.
Vaidyanathan PP: Multirate Systems and Filter Banks. Prentice Hall, Englewood Cliffs, NJ, USA; 1993.
Horn RA, Johnson CR: Matrix Analysis. Cambridge University Press, Cambridge, UK; 1985.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://doi.org/creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Chiang, HT., Phoong, SM. & Lin, YP. Design of Nonuniform Filter Bank Transceivers for Frequency Selective Channels. EURASIP J. Adv. Signal Process. 2007, 061396 (2006). https://doi.org/10.1155/2007/61396
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/61396
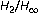 filtering design in multirate transmultiplexer systems: LMI approach. IEEE Transactions on Signal Processing 2001,49(11):2693–2701. 10.1109/78.960416
filtering design in multirate transmultiplexer systems: LMI approach. IEEE Transactions on Signal Processing 2001,49(11):2693–2701. 10.1109/78.960416