- Research Article
- Open access
- Published:
Estimation of Spectral Exponent Parameter of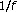 Process in Additive White Background Noise
Process in Additive White Background Noise
EURASIP Journal on Advances in Signal Processing volume 2007, Article number: 063219 (2007)
Abstract
An extension to the wavelet-based method for the estimation of the spectral exponent,  , in a
, in a  process and in the presence of additive white noise is proposed. The approach is based on eliminating the effect of white noise by a simple difference operation constructed on the wavelet spectrum. The
process and in the presence of additive white noise is proposed. The approach is based on eliminating the effect of white noise by a simple difference operation constructed on the wavelet spectrum. The  parameter is estimated as the slope of a linear function. It is shown by simulations that the proposed method gives reliable results. Global positioning system (GPS) time-series noise is analyzed and the results provide experimental verification of the proposed method.
parameter is estimated as the slope of a linear function. It is shown by simulations that the proposed method gives reliable results. Global positioning system (GPS) time-series noise is analyzed and the results provide experimental verification of the proposed method.
References
Wornell GW:Wavelet-based representations for the
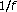 family of fractal processes. Proceedings of the IEEE 1993,81(10):1428-1450. 10.1109/5.241506
family of fractal processes. Proceedings of the IEEE 1993,81(10):1428-1450. 10.1109/5.241506Agnew DC: The time-domain behavior of power-law noises. Geophysical Research Letters 1992,19(4):333-336. 10.1029/91GL02832
Langbein J, Johnson H: Correlated errors in geodetic time series: implications for time-dependent deformation. Journal of Geophysical Research 1997,102(B1):591-604. 10.1029/96JB02945
Mao A, Harrison CGA, Dixon TH: Noise in GPS coordinate time series. Journal of Geophysical Research 1999,104(B2):2797-2816. 10.1029/1998JB900033
Williams SDP, Bock Y, Fang P, et al.: Error analysis of continuous GPS position time series. Journal of Geophysical Research 2004,109(B3):1-19.
Leland WE, Taqqu MS, Willinger W, Wilson DV: On the self-similar nature of Ethernet traffic (extended version). IEEE/ACM Transactions on Networking 1994,2(1):1-15. 10.1109/90.282603
Mandelbrot BB, van Ness JW: Fractional Brownian motions, fractional noises and applications. SIAM Review 1968,10(4):422-437. 10.1137/1010093
Wornell GW, Oppenheim AV: Estimation of fractal signals from noisy measurements using wavelets. IEEE Transactions on Signal Processing 1992,4(3):611-623.
Ninness B:Estimation of
 noise. IEEE Transactions on Information Theory 1998,44(1):32-46. 10.1109/18.650986
noise. IEEE Transactions on Information Theory 1998,44(1):32-46. 10.1109/18.650986Du L, Zhuang Y, Wu Y:
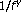 noise separated from white noise with wavelet denoising. Microelectronics Reliability 2002,42(2):183-188. 10.1016/S0026-2714(01)00249-9
noise separated from white noise with wavelet denoising. Microelectronics Reliability 2002,42(2):183-188. 10.1016/S0026-2714(01)00249-9Kaplan LM, Kuo C-CJ: Fractal estimation from noisy data via discrete fractional Gaussian noise (DFGN) and the Haar basis. IEEE Transactions on Signal Processing 1993,41(12):3554-3562. 10.1109/78.258096
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://doi.org/creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Baykut, S., Akgül, T. & Ergintav, S. Estimation of Spectral Exponent Parameter of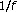 Process in Additive White Background Noise.
EURASIP J. Adv. Signal Process. 2007, 063219 (2007). https://doi.org/10.1155/2007/63219
Process in Additive White Background Noise.
EURASIP J. Adv. Signal Process. 2007, 063219 (2007). https://doi.org/10.1155/2007/63219
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/63219
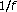 family of fractal processes. Proceedings of the IEEE 1993,81(10):1428-1450. 10.1109/5.241506
family of fractal processes. Proceedings of the IEEE 1993,81(10):1428-1450. 10.1109/5.241506 noise. IEEE Transactions on Information Theory 1998,44(1):32-46. 10.1109/18.650986
noise. IEEE Transactions on Information Theory 1998,44(1):32-46. 10.1109/18.650986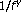 noise separated from white noise with wavelet denoising. Microelectronics Reliability 2002,42(2):183-188. 10.1016/S0026-2714(01)00249-9
noise separated from white noise with wavelet denoising. Microelectronics Reliability 2002,42(2):183-188. 10.1016/S0026-2714(01)00249-9