- Research Article
- Open access
- Published:
An Approach for Synthesis of Modulated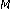 -Channel FIR Filter Banks Utilizing the Frequency-Response Masking Technique
-Channel FIR Filter Banks Utilizing the Frequency-Response Masking Technique
EURASIP Journal on Advances in Signal Processing volume 2007, Article number: 068285 (2006)
Abstract
The frequency-response masking (FRM) technique was introduced as a means of generating linear-phase FIR filters with narrow transition band and low arithmetic complexity. This paper proposes an approach for synthesizing modulated maximally decimated FIR filter banks (FBs) utilizing the FRM technique. A new tailored class of FRM filters is introduced and used for synthesizing nonlinear-phase analysis and synthesis filters. Each of the analysis and synthesis FBs is realized with the aid of only three subfilters, one cosine-modulation block, and one sine-modulation block. The overall FB is a near-perfect reconstruction (NPR) FB which in this case means that the distortion function has a linear-phase response but small magnitude errors. Small aliasing errors are also introduced by the FB. However, by allowing these small errors (that can be made arbitrarily small), the arithmetic complexity can be reduced. Compared to conventional cosine-modulated FBs, the proposed ones lower significantly the overall arithmetic complexity at the expense of a slightly increased overall FB delay in applications requiring narrow transition bands. Compared to other proposals that also combine cosine-modulated FBs with the FRM technique, the arithmetic complexity can typically be reduced by in specifications with narrow transition bands. Finally, a general design procedure is given for the proposed FBs and examples are included to illustrate their benefits.
in specifications with narrow transition bands. Finally, a general design procedure is given for the proposed FBs and examples are included to illustrate their benefits.
References
Crochiere RE, Rabiner LR: Multirate Digital Signal Processing. Prentice-Hall, Englewood Cliffs, NJ, USA; 1983.
Vaidyanathan PP: Multirate Systems and Filter Banks. Prentice-Hall, Englewood Cliffs, NJ, USA; 1993.
Fliege NJ: Multirate Digital Signal Processing. John Wiley & Sons, New York, NY, USA; 1994.
Saramäki T: A generalized class of cosine modulated filter banks. Proceedings of the 1st International Workshop on Transforms and Filter Banks, February 1998, Tampere, Finland 336–365.
Bregović R, Saramäki T: An efficient approach for designing nearly perfect-reconstruction low-delay cosine-modulated filter banks. Proceedings of the IEEE International Symposium on Circuits and Systems, May 2002, Phoenix, Ariz, USA 1: 825–828.
Svensson L, Löwenborg P, Johansson H: A class of cosine-modulated causal IIR filter banks. Proceedings of the 9th International Conference on Electronics, Circuits and Systems (ICECS '02), September 2002, Dubrovnik, Croatia 3: 915–918.
Eshraghi A, Fiez TS: A comparative analysis of parallel delta-sigma ADC architectures. IEEE Transactions on Circuits and Systems I: Regular Papers 2004,51(3):450–458. 10.1109/TCSI.2004.823663
Kaiser JF:Nonrecursive digital filter design using
 -sinh window function. Proceedings of the IEEE Symposium on Circuits & Systems (ISCAS '74), April 1974, San Francisco, Calif, USA 3: 20–23.
-sinh window function. Proceedings of the IEEE Symposium on Circuits & Systems (ISCAS '74), April 1974, San Francisco, Calif, USA 3: 20–23.Saramäki T: Finite impulse response filter design. In Handbook for Digital Signal Processing. Edited by: Mitra SK, Kaiser JF. John Wiley & Sons, New York, NY, USA; 1993:155–277. chapter 4
Lim YC: Frequency-response masking approach for the synthesis of sharp linear phase digital filters. IEEE Transactions on Circuits and Systems 1986,33(4):357–364. 10.1109/TCS.1986.1085930
Lim YC, Lian Y: The optimum design of one and two-dimensional FIR filters using the frequency response masking technique. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing 1993,40(2):88–95. 10.1109/82.219838
Saramäki T: Design of computationally efficient FIR filters using periodic subfilters as building blocks. In The Circuits and Filters Handbook. Edited by: Chen WK. CRC Press, Boca Raton, Fla, USA; 1995:2578–2601.
Johansson H, Saramäki T: Two-channel FIR filter banks based on the frequency-response masking approach. Proceedings of the 2nd International Workshop on Transforms Filter Banks, March 1999, Brandenburg an der Havel, Germany
Johansson H: New classes of frequency-response masking FIR filters. Proceedings of the IEEE International Symposium on Circuits and Systems, May 2000, Geneva, Switzerland 3: 81–84.
Diniz PSR, De Barcellos LCR, Netto SL: Design of cosine-modulated filter bank prototype filters using the frequency-response masking approach. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '01), May 2001, Salt Lake, Utah, USA 6: 3621–3624.
Furtado MB Jr., Diniz PSR, Netto SL: Optimized prototype filter based on the FRM approach for cosine-modulated filter banks. Circuits, Systems, and Signal Processing 2003,22(2):193–210.
Netto SL, De Barcellos LCR, Diniz PSR: Efficient design of narrowband cosine-modulated filter banks using a two-stage frequency-response masking approach. Journal of Circuits, Systems and Computers 2003,12(5):631–642. 10.1142/S0218126603001057
Diniz PSR, De Barcellos LCR, Netto SL: Design of high-resolution cosine-modulated transmultiplexers with sharp transition band. IEEE Transactions on Signal Processing 2004,52(5):1278–1288. 10.1109/TSP.2004.826157
Furtado MB Jr., Diniz PSR, Netto SL, Saramäki T: On the design of high-complexity cosine-modulated transmultiplexers based on the frequency-response masking approach. IEEE Transactions on Circuits and Systems I: Regular Papers 2005,52(11):2413–2426.
Svensson L, Löwenborg P, Johansson H:Modulated
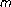 -channel FIR filter banks utilizing the frequency response masking approach. Proceedings of the IEEE Nordic Signal Processing Symposium (NORSIG '02), October 2002, Hurtigruta, Tromsö-Trondheim, Norway
-channel FIR filter banks utilizing the frequency response masking approach. Proceedings of the IEEE Nordic Signal Processing Symposium (NORSIG '02), October 2002, Hurtigruta, Tromsö-Trondheim, NorwayRosenbaum L, Löwenborg P, Johansson H: Cosine and sine modulated FIR filter banks utilizing the frequency-response masking approach. Proceedings of the IEEE International Symposium on Circuits and Systems, May 2003, Bangkok, Thailand 3: 882–885.
McClellan JH, Parks TW, Rabiner LR: A computer program for designing optimum FIR linear phase digital filters. IEEE Transactions on Audio and Electroacoustics 1973,21(6):506–526. 10.1109/TAU.1973.1162525
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Rosenbaum, L., Löwenborg, P. & Johansson, H. An Approach for Synthesis of Modulated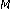 -Channel FIR Filter Banks Utilizing the Frequency-Response Masking Technique.
EURASIP J. Adv. Signal Process. 2007, 068285 (2006). https://doi.org/10.1155/2007/68285
-Channel FIR Filter Banks Utilizing the Frequency-Response Masking Technique.
EURASIP J. Adv. Signal Process. 2007, 068285 (2006). https://doi.org/10.1155/2007/68285
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/68285
 -sinh window function. Proceedings of the IEEE Symposium on Circuits & Systems (ISCAS '74), April 1974, San Francisco, Calif, USA 3: 20–23.
-sinh window function. Proceedings of the IEEE Symposium on Circuits & Systems (ISCAS '74), April 1974, San Francisco, Calif, USA 3: 20–23.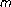 -channel FIR filter banks utilizing the frequency response masking approach. Proceedings of the IEEE Nordic Signal Processing Symposium (NORSIG '02), October 2002, Hurtigruta, Tromsö-Trondheim, Norway
-channel FIR filter banks utilizing the frequency response masking approach. Proceedings of the IEEE Nordic Signal Processing Symposium (NORSIG '02), October 2002, Hurtigruta, Tromsö-Trondheim, Norway