- Research Article
- Open access
- Published:
High-Selectivity Filter Banks for Spectral Analysis of Music Signals
EURASIP Journal on Advances in Signal Processing volume 2007, Article number: 094704 (2006)
Abstract
This paper approaches, under a unified framework, several algorithms for the spectral analysis of musical signals. Such algorithms include the fast Fourier transform (FFT), the fast filter bank (FFB), the constant- transform (C
transform (C T), and the bounded-
T), and the bounded- transform (B
transform (B T), previously known from the associated literature. Two new methods are then introduced, namely, the constant-
T), previously known from the associated literature. Two new methods are then introduced, namely, the constant- fast filter bank (C
fast filter bank (C FFB) and the bounded-
FFB) and the bounded- fast filter bank (B
fast filter bank (B FFB), combining the positive characteristics of the previously mentioned algorithms. The provided analyses indicate that the proposed B
FFB), combining the positive characteristics of the previously mentioned algorithms. The provided analyses indicate that the proposed B FFB achieves an excellent compromise between the reduced computational effort of the FFT, the high selectivity of each output channel of the FFB, and the efficient distribution of frequency channels associated to the C
FFB achieves an excellent compromise between the reduced computational effort of the FFT, the high selectivity of each output channel of the FFB, and the efficient distribution of frequency channels associated to the C T and B
T and B T methods. Examples are included to illustrate the performances of these methods in the spectral analysis of music signals.
T methods. Examples are included to illustrate the performances of these methods in the spectral analysis of music signals.
References
Farhang-Boroujeny B, Lim YC: A comment on the computational complexity of sliding FFT. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing 1992,39(12):875–876. 10.1109/82.208583
Lim YC, Farhang-Boroujeny B: Fast filter bank (FFB). IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing 1992,39(5):316–318. 10.1109/82.142033
William D, Brown E: Theoretical Foundations of Music. Wadsworth, Belmont, Calif, USA; 1978.
Brown JC:Calculation of a constant
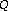 spectral transform. Journal of the Acoustical Society of America 1991,89(1):425–434. 10.1121/1.400476
spectral transform. Journal of the Acoustical Society of America 1991,89(1):425–434. 10.1121/1.400476Brown JC, Puckette MS:An efficient algorithm for the calculation of a constant
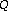 transform. Journal of the Acoustical Society of America 1992,92(5):2698–2701. 10.1121/1.404385
transform. Journal of the Acoustical Society of America 1992,92(5):2698–2701. 10.1121/1.404385Kashima KL, Mont-Reynaud B:The bounded-
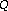 approach to time-varying spectral analysis. In Tech. Rep. STAN-M-28. Stanford University, Department of Music, Stanford, Calif, USA; 1985.
approach to time-varying spectral analysis. In Tech. Rep. STAN-M-28. Stanford University, Department of Music, Stanford, Calif, USA; 1985.Graziosi DB, Dos Santos CN, Netto SL, Biscainho LWP:A constant-
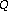 spectral transformation with improved frequency response. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '04), May 2004, Vancouver, Canada 5: 544–547.
spectral transformation with improved frequency response. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '04), May 2004, Vancouver, Canada 5: 544–547.Dos Santos CN, Netto SL, Biscainho LWP, Graziosi DB:A modified constant-
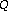 transform for audio signals. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '04), May 2004, Montreal, Canada 2: 469–472.
transform for audio signals. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '04), May 2004, Montreal, Canada 2: 469–472.Diniz FCCB, Kothe I, Biscainho LWP, Netto SL:A bounded-
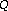 fast filter bank for audio signal analysis. Proceedings of IEEE International Telecommunications Symposium (ITS '06), September 2006, Fortaleza, Brazil 1:
fast filter bank for audio signal analysis. Proceedings of IEEE International Telecommunications Symposium (ITS '06), September 2006, Fortaleza, Brazil 1:Diniz PSR, da Silva EAB, Netto SL: Digital Signal Processing: System Analysis and Design. Cambridge University Press, Cambridge, UK; 2002.
Cooley JW, Tukey JW: An algorithm for the machine calculation of complex fourier series. Mathematics of Computation 1965,19(90):297–301. 10.1090/S0025-5718-1965-0178586-1
Haykin S, Van Veen B: Signals and Systems. 2nd edition. John wiley & Sons, Hoboken, NJ, USA; 2002.
Vaidyanathan PP: Multirate Systems and Filter Banks. Prentice Hall, Upper Saddle River, NJ, USA; 1992.
Lim YC: Frequency-response masking approach for the synthesis of sharp linear phase digital filters. IEEE Transactions on Circuits and Systems 1986,33(4):357–364. 10.1109/TCS.1986.1085930
Lim YC, Farhang-Boroujeny B: Analysis and optimum design of the FFB. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '94), June 1994, London, UK 2: 509–512.
Wei LJ, Lim YC: Designing the fast filter bank with a minimum complexity criterion. Proceedings of the 7th International Symposium on Signal Processing and Its Applications (ISSPA '03), July 2003, Paris, France 2: 279–282.
Lim YC, Wei LJ: Matrix formulation: fast filter bank. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '04), May 2004, Montreal, Canada 5: 133–136.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Diniz, F.C.C.B., Kothe, I., Netto, S.L. et al. High-Selectivity Filter Banks for Spectral Analysis of Music Signals. EURASIP J. Adv. Signal Process. 2007, 094704 (2006). https://doi.org/10.1155/2007/94704
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/94704
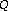 spectral transform. Journal of the Acoustical Society of America 1991,89(1):425–434. 10.1121/1.400476
spectral transform. Journal of the Acoustical Society of America 1991,89(1):425–434. 10.1121/1.400476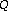 transform. Journal of the Acoustical Society of America 1992,92(5):2698–2701. 10.1121/1.404385
transform. Journal of the Acoustical Society of America 1992,92(5):2698–2701. 10.1121/1.404385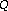 approach to time-varying spectral analysis. In Tech. Rep. STAN-M-28. Stanford University, Department of Music, Stanford, Calif, USA; 1985.
approach to time-varying spectral analysis. In Tech. Rep. STAN-M-28. Stanford University, Department of Music, Stanford, Calif, USA; 1985.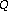 spectral transformation with improved frequency response. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '04), May 2004, Vancouver, Canada 5: 544–547.
spectral transformation with improved frequency response. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '04), May 2004, Vancouver, Canada 5: 544–547.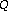 transform for audio signals. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '04), May 2004, Montreal, Canada 2: 469–472.
transform for audio signals. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '04), May 2004, Montreal, Canada 2: 469–472.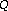 fast filter bank for audio signal analysis. Proceedings of IEEE International Telecommunications Symposium (ITS '06), September 2006, Fortaleza, Brazil 1:
fast filter bank for audio signal analysis. Proceedings of IEEE International Telecommunications Symposium (ITS '06), September 2006, Fortaleza, Brazil 1: