- Research Article
- Open access
- Published:
Fast Nonnegative Matrix Factorization and Its Application for Protein Fold Recognition
EURASIP Journal on Advances in Signal Processing volume 2006, Article number: 071817 (2006)
Abstract
Linear and unsupervised dimensionality reduction via matrix factorization with nonnegativity constraints is studied. Because of these constraints, it stands apart from other linear dimensionality reduction methods. Here we explore nonnegative matrix factorization in combination with three nearest-neighbor classifiers for protein fold recognition. Since typically matrix factorization is iteratively done, convergence, can be slow. To speed up convergence, we perform feature scaling (normalization) prior to the beginning of iterations. This results in a significantly (more than 11 times) faster algorithm. Justification of why it happens is provided. Another modification of the standard nonnegative matrix factorization algorithm is concerned with combining two known techniques for mapping unseen data. This operation is typically necessary before classifying the data in low-dimensional space. Combining two mapping techniques can yield better accuracy than using either technique alone. The gains, however, depend on the state of the random number generator used for initialization of iterations, a classifier, and its parameters. In particular, when employing the best out of three classifiers and reducing the original dimensionality by around 30%, these gains can reach more than 4%, compared to the classification in the original, high-dimensional space.
References
Jolliffe IT: Principal Component Analysis. Springer, New York, NY, USA; 1986.
Common P: Independent component analysis. Proceedings of the International Signal Processing Workshop on Higher-Order Statistics, July 1991, Chamrousse, France 111–120.
Lee DD, Seung HS: Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401(6755):788–791. 10.1038/44565
Tsuge S, Shishibori M, Kuroiwa S, Kita K: Dimensionality reduction using non-negative matrix factorization for information retrieval. Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, July–October 2001, Tucson, Ariz, USA 2: 960–965.
Xu B, Lu J, Huang G: A constrained non-negative matrix factorization in information retrieval. Proceedings of the IEEE International Conference on Information Reuse and Integration (IRI '03), October 2003, Las Vegas, Nev, USA 273–277.
Buciu I, Pitas I: Application of non-negative and local non negative matrix factorization to facial expression recognition. Proceedings of the 17th International Conference on Pattern Recognition (ICPR '04), 2004, Cambridge, UK 1: 288–291.
Chen X, Gu L, Li SZ, Zhang H-J: Learning representative local features for face detection. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '01), December 2001, Kauai, Hawaii, USA 1: I-1126–I-1131.
Feng T, Li SZ, Shum H-Y, Zhang H-Y: Local non-negative matrix factorization as a visual representation. Proceedings of the 2nd International Conference on Development and Learning, June 2002, Cambridge, Mass, USA 178–183.
Guillamet D, Vitria J: Discriminant basis for object classification. Proceedings of the 11th International Conference on Image Analysis and Processing, September 2001, Palermo, Italy 256–261.
Guillamet D, Vitrià J: Evaluation of distance metrics for recognition based on non-negative matrix factorization. Pattern Recognition Letters 2003, 24(9–10):1599–1605. 10.1016/S0167-8655(02)00399-9
Guillamet D, Vitrià J, Schiele B: Introducing a weighted non-negative matrix factorization for image classification. Pattern Recognition Letters 2003, 24(14):2447–2454. 10.1016/S0167-8655(03)00089-8
Rajapakse M, Wyse L: NMF vs ICA for face recognition. Proceedings of the 3rd International Symposium on Image and Signal Processing and Analysis (ISPA '03), September 2003, Rome, Italy 2: 605–610.
Ramanath R, Snyder WE, Qi H: Eigenviews for object recognition in multispectral imaging systems. Proceedings of the 32nd Applied Imagery Pattern Recognition Workshop, October 2003, Washington, DC, USA 33–38.
Saul LK, Lee DD: Multiplicative updates for classification by mixture models. In Advances in Neural and Information Processing Systems. Volume 14. Edited by: Dietterich TG, Becker S, Ghahramani Z. MIT Press, Cambridge, Mass, USA; 2002:897–904.
Wang Y, Jia Y, Hu C, Turk M: Fisher non-negative matrix factorization for learning local features. Proceedings of the 6th Asian Conference on Computer Vision, January 2004, Jeju Island, Korea
Hoyer PO: Non-negative matrix factorization with sparseness constraints. Journal of Machine Learning Research 2004, 5: 1457–1469.
Li Y, Cichocki A: Sparse representation of images using alternating linear programming. Proceedings of the 7th International Symposium on Signal Processing and Its Applications (ISSPA '03), July 2003, Paris, France 1: 57–60.
Liu W, Zheng N, Lu X: Non-negative matrix factorization for visual coding. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP~'03), April 2003, Hong Kong 3: 293–296.
Behnke S: Discovering hierarchical speech features using convolutional non-negative matrix factorization. Proceedings of the International Joint Conference on Neural Networks, July 2003, Portland, Ore, USA 4: 2758–2763.
Cho Y-C, Choi S, Bang S-Y: Non-negative component parts of sound for classification. Proceedings of the 3rd IEEE International Symposium on Signal Processing and Information Technology (ISSPIT '03), December 2003, Darmstadt, Germany 633–636.
Novak M, Mammone R: Use of non-negative matrix factorization for language model adaptation in a lecture transcription task. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '01), May 2001, Salt Lake City, Utah, USA 1: 541–544.
Smaragdis P, Brown JC: Non-negative matrix factorization for polyphonic music transcription. Proceedings of the IEEE Workshop on Applications of Signal Processing to Audio and Acoustics, October 2003, New Paltz, NY, USA 177–180.
Lu J, Xu B, Yang H: Matrix dimensionality reduction for mining Web logs. Proceedings of the IEEE/WIC International Conference on Web Intelligence, October 2003, Halifax, NS, Canada 405–408.
Mao Y, Saul LK: Modeling distances in large-scale networks by matrix factorization. Proceedings of the ACM Internet Measurement Conference, October 2004, Sicily, Italy 278–287.
Cooper M, Foote J: Summarizing video using non-negative similarity matrix factorization. Proceedings of the IEEE Workshop on Multimedia Signal Processing, December 2002, St.Thomas, Virgin Islands, USA 25–28.
Lawrence J, Rusinkiewicz S, Ramamoorthi R: Efficient BRDF importance sampling using a factored representation. ACM Transactions on Graphics 2004, 23(3):496–505. Special issue: Proceedings of the 2004 SIGGRAPH Conference 10.1145/1015706.1015751
Plumbley MD, Oja E: A "nonnegative PCA" algorithm for independent component analysis. IEEE Transactions on Neural Networks 2004, 15(1):66–76. 10.1109/TNN.2003.820672
Bologna G, Appel RD: A comparaison study on protein fold recognition. Proceedings of the 9th International Conference on Neural Information Processing (ICONIP '02), November 2002, Singapore 5: 2492–2496.
Chung I-F, Huang C-D, Shen Y-H, Lin C-T: Recognition of structure classification of protein folding by NN and SVM hierarchical learning architecture. In Artificial Neural Networks and Neural Information Processing (ICANN/ICONIP~'03), June 2003, Istanbul, Turkey, Lecture Notes in Computer Science Edited by: Kaynak O, Alpaydin E, Oja E, Xu L. 2714: 1159–1167.
Pal NR, Chakraborty D: Some new features for protein fold recognition. In Artificial Neural Networks and Neural Information Processing (ICANN/ICONIP '03), June 2003, Istanbul, Turkey, Lecture Notes in Computer Science Edited by: Kaynak O, Alpaydin E, Oja E, Xu L. 2714: 1176–1183.
Ding CHQ, Dubchak I: Multi-class protein fold recognition using support vector machines and neural networks. Bioinformatics 2001, 17(4):349–358. 10.1093/bioinformatics/17.4.349
Okun O:Protein fold recognition with
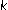 -local hyperplane distance nearest neighbor algorithm. Proceedings of the 2nd European Workshop on Data Mining and Text Mining for Bioinformatics, September 2004, Pisa, Italy 47–53.
-local hyperplane distance nearest neighbor algorithm. Proceedings of the 2nd European Workshop on Data Mining and Text Mining for Bioinformatics, September 2004, Pisa, Italy 47–53.Lo Conte L, Ailey B, Hubbard TJP, Brenner SE, Murzin AG, Chothia C: SCOP: a structural classification of proteins database. Nucleic Acids Research 2000, 28(1):257–259. 10.1093/nar/28.1.257
Huang C-D, Chung I-F, Pal NR, Lin C-T: Machine learning for multi-class protein fold classification based on neural networks with feature gating. In Artificial Neural Networks and Neural Information Processing (ICANN/ICONIP~'03), June 2003, Istanbul, Turkey, Lecture Notes in Computer Science Edited by: Kaynak O, Alpaydin E, Oja E, Xu L. 2714: 1168–1175.
Okun O: Feature normalization and selection for protein fold recognition. Proceedings of the 11th Finnish Artificial Intelligence Conference, September 2004, Vantaa, Finland 207–221.
Cover T, Hart P: Nearest neighbor pattern classification. IEEE Transactions on Information Theory 1967, 13(1):21–27.
Yu K, Ji L, Zhang X: Kernel nearest-neighbor algorithm. Neural Processing Letters 2002, 15(2):147–156. 10.1023/A:1015244902967
Vincet P, Bengio Y:
 -local hyperlane and convex distance nearest neighbor algorithms. In Advances in Neural Information Processing Systems. Volume 14. Edited by: Dietterich TG, Becker S, Ghahramani Z. MIT Press, Cambridge, Mass, USA; 2002:985–992.
-local hyperlane and convex distance nearest neighbor algorithms. In Advances in Neural Information Processing Systems. Volume 14. Edited by: Dietterich TG, Becker S, Ghahramani Z. MIT Press, Cambridge, Mass, USA; 2002:985–992.Okun O:
 -local hyperplane distance nearest neighbor algorithm and protein fold recognition. Pattern Recognition and Image Analysis 2006, 16(1):19–22. 10.1134/S1054661806010068
-local hyperplane distance nearest neighbor algorithm and protein fold recognition. Pattern Recognition and Image Analysis 2006, 16(1):19–22. 10.1134/S1054661806010068Okun O: Non-negative matrix factorization and classifiers: experimental study. Proceedings of the 4th IASTED International Conference on Visualization, Imaging, and Image Processing (VIIP '04), September 2004, Marbella, Spain 550–555.
Lee DD, Seung HS: Algorithms for non-negative matrix factorization. In Advances in Neural and Information Processing Systems. Volume 13. Edited by: Leen TK, Dietterich TG, Tresp V. MIT Press, Cambridge, Mass, USA; 2001:556–562.
Kullback S, Leibler RA: On information and sufficiency. The Annals of Mathematical Statistics 1951, 22(1):79–86. 10.1214/aoms/1177729694
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Okun, O., Priisalu, H. Fast Nonnegative Matrix Factorization and Its Application for Protein Fold Recognition. EURASIP J. Adv. Signal Process. 2006, 071817 (2006). https://doi.org/10.1155/ASP/2006/71817
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/ASP/2006/71817
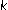 -local hyperplane distance nearest neighbor algorithm. Proceedings of the 2nd European Workshop on Data Mining and Text Mining for Bioinformatics, September 2004, Pisa, Italy 47–53.
-local hyperplane distance nearest neighbor algorithm. Proceedings of the 2nd European Workshop on Data Mining and Text Mining for Bioinformatics, September 2004, Pisa, Italy 47–53. -local hyperlane and convex distance nearest neighbor algorithms. In Advances in Neural Information Processing Systems. Volume 14. Edited by: Dietterich TG, Becker S, Ghahramani Z. MIT Press, Cambridge, Mass, USA; 2002:985–992.
-local hyperlane and convex distance nearest neighbor algorithms. In Advances in Neural Information Processing Systems. Volume 14. Edited by: Dietterich TG, Becker S, Ghahramani Z. MIT Press, Cambridge, Mass, USA; 2002:985–992. -local hyperplane distance nearest neighbor algorithm and protein fold recognition. Pattern Recognition and Image Analysis 2006, 16(1):19–22. 10.1134/S1054661806010068
-local hyperplane distance nearest neighbor algorithm and protein fold recognition. Pattern Recognition and Image Analysis 2006, 16(1):19–22. 10.1134/S1054661806010068