- Research Article
- Open access
- Published:
The Finite Heisenberg-Weyl Groups in Radar and Communications
EURASIP Journal on Advances in Signal Processing volume 2006, Article number: 085685 (2006)
Abstract
We investigate the theory of the finite Heisenberg-Weyl group in relation to the development of adaptive radar and to the construction of spreading sequences and error-correcting codes in communications. We contend that this group can form the basis for the representation of the radar environment in terms of operators on the space of waveforms. We also demonstrate, following recent developments in the theory of error-correcting codes, that the finite Heisenberg-Weyl groups provide a unified basis for the construction of useful waveforms/sequences for radar, communications, and the theory of error-correcting codes.
References
Folland GB: Harmonic Analysis in Phase Space. Princeton University Press, Princeton, NJ, USA; 1989.
Miller W: Topics in harmonic analysis with applications to radar and sonar. In Radar and Sonar, Part I, IMA Volumes in Mathematics and Its Applications. Edited by: Blahut R, Miller W, Wilcox C. Springer, New York, NY, USA; 1991.
Auslander L, Tolimieri R: Radar ambiguity functions and group theory. SIAM Journal on Mathematical Analysis 1985, 16(3):577–601. 10.1137/0516043
Mackey GW: Some remarks on symplectic automorphisms. Proceedings of the American Mathematical Society 1965, 16: 393–397. 10.1090/S0002-9939-1965-0177064-5
Segal IE: Transforms for operators and symplectic automorphisms over a locally compact abelian group. Mathematica Scandinavica 1963, 13: 31–43.
Weil A: Sur certains groupes d'opérateurs unitaires. Acta Mathematica 1964, 111: 143–211. 10.1007/BF02391012
Richman MS, Parks TW, Shenoy RG: Discrete-time, discrete-frequency, time-frequency analysis. IEEE Transactions on Signal Processing 1998, 46(6):1517–1527. 10.1109/78.678465
Tolimieri R, An M: Time-Frequency Representations. Birkhäuser Boston, Boston, Mass, USA; 1998.
Bottomley GE: Signature sequence selection in a CDMA system with orthogonal coding. IEEE Transactions on Vehicular Technology 1993, 42(1):62–68. 10.1109/25.192388
Yang K, Kim Y-K, Vijay Kumar P: Quasi-orthogonal sequences for code-division multiple-access systems. IEEE Transactions on Information Theory 2000, 46(3):982–993. 10.1109/18.841175
Welti G: Quaternary codes for pulsed radar. IEEE Transactions on Information Theory 1960, 6(3):400–408. 10.1109/TIT.1960.1057572
Golay M: Complementary series. IEEE Transactions on Information Theory 1961, 7(2):82–87. 10.1109/TIT.1961.1057620
Budisin SZ, Popovic BM, Indjin IM: Designing radar signals using complementary sequences. IEEE Transactions on Aerospace and Electronic Systems 1985, 21(2):170–179.
Macwilliams FJ, Sloane NJA: The Theory of Error Correcting Codes. North-Holland Elsevier, Amsterdam, The Netherlands; 1983.
Calderbank AR, Cameron PJ, Kantor WM, Seidel JJ:
 -Kerdock codes, orthogonal spreads, and extremal euclidean line-sets. Proceedings of the London Mathematical Society 1997, 75(2):436–480. 10.1112/S0024611597000403
-Kerdock codes, orthogonal spreads, and extremal euclidean line-sets. Proceedings of the London Mathematical Society 1997, 75(2):436–480. 10.1112/S0024611597000403Reiter H: Classical Harmonic Analysis and Locally Compact Groups. Oxford University Press, London, UK; 1968.
Renes JM, Blume-Kohout R, Scott AJ, Caves CM: Symmetric informationally complete quantum measurements. Journal of Mathematical Physics 2004, 45(6):2171–2180. 10.1063/1.1737053
Wilcox CH: The synthesis problem for radar ambiguity functions. In Radar and Sonar, Part I, IMA Series in Mathematics and Its Applications. Volume 32. Springer, New York, NY, USA; 1991:229–260.
Feichtinger HG, Kozek W: Quantization of TF lattice-invariant operators on elementary LCA groups. In Gabor Analysis and Algorithms: Theory and Applications, Applied and Numerical Harmonic Analysis. Edited by: Feichtinger HG, Strohmer T. Birkhäuser, Boston, Mass, USA; 1998:233–266. chapter 7
Delsarte P, Goethals JM, Seidel JJ: Bounds for systems of lines and Jacobi polynomials. Philips Research Reports 1975, 30(3):91–105.
Lemmens PWH, Seidel JJ: Equiangular lines. Journal of Algebra 1973, 24(3):494–512. 10.1016/0021-8693(73)90123-3
Hoggar SG: 64 lines from a quaternionic polytope. Geometriae Dedicata 1998, 69(3):287–289. 10.1023/A:1005009727232
Strohmer T, Heath RW Jr.: Grassmannian frames with applications to coding and communication. Applied and Computational Harmonic Analysis 2003, 14(3):257–275. 10.1016/S1063-5203(03)00023-X
Perelomov AM: Generalized Coherent States and Their Applications. Springer, Berlin, Germany; 1986.
Daubechies I: Ten Lectures on Wavelets. SIAM, Philadelphia, Pa, USA; 1992.
Perelomov AM: Coherent states for arbitrary Lie group. Communications in Mathematical Physics 1972, 26(3):222–236. 10.1007/BF01645091
Brown EH: Generalizations of kervaire's invariant. Annals of Mathematics 1972, 95: 368–383. 10.2307/1970804
Pottie GJ, Calderbank AR: Channel coding strategies for cellular radio. IEEE Transactions on Vehicular Technology 1995, 44(4):763–770. 10.1109/25.467960
Costas JP: A study of a class of detection waveforms having nearly ideal range-Doppler ambiguity properties. Proceedings of the IEEE 1984, 72(8):996–1009.
Kerdock AM: A class of low rate nonlinear binary codes. Information and Control 1972, 20(2):182–187. 10.1016/S0019-9958(72)90376-2
Hammons AR Jr., Kumar PV, Calderbank AR, Sloane NJA, Solé P:The
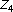 -linearity of Kerdock, Preparata, Goethals, and related codes. IEEE Transactions on Information Theory 1994, 40(2):301–319. 10.1109/18.312154
-linearity of Kerdock, Preparata, Goethals, and related codes. IEEE Transactions on Information Theory 1994, 40(2):301–319. 10.1109/18.312154Wootters WK, Fields BD: Optimal state-determination by mutually unbiased measurements. Annals of Physics 1989, 191(2):363–381. 10.1016/0003-4916(89)90322-9
Davis JA, Jedwab J: Peak-to-mean power control in OFDM, Golay complementary sequences, and Reed-Muller codes. IEEE Transactions on Information Theory 1999, 45(7):2397–2417. 10.1109/18.796380
Shapiro HS: Extremal problems for polynomials and power series, Sc.M. thesis. Massachusetts Institute of Technology, Cambridge, Mass, USA; 1951.
Golay M: Multislit spectrometry. Journal of the Optical Society of America June 1949, 39: 437–444. 10.1364/JOSA.39.000437
Budisin SZ: New complementary pairs of sequences. Electronics Letters 1990, 26(13):881–883. 10.1049/el:19900576
Craigen R: Complex golay sequences. Journal of Combinatorial Mathematics and Combinatorial Computing 1994, 15: 161–169.
Calderbank AR, Rains EM, Shor PW, Sloane NJA: Quantum error correction via codes over GF(4). IEEE Transactions on Information Theory 1998, 44(4):1369–1387. 10.1109/18.681315
Author information
Authors and Affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Howard, S.D., Calderbank, A.R. & Moran, W. The Finite Heisenberg-Weyl Groups in Radar and Communications. EURASIP J. Adv. Signal Process. 2006, 085685 (2006). https://doi.org/10.1155/ASP/2006/85685
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/ASP/2006/85685
 -Kerdock codes, orthogonal spreads, and extremal euclidean line-sets. Proceedings of the London Mathematical Society 1997, 75(2):436–480. 10.1112/S0024611597000403
-Kerdock codes, orthogonal spreads, and extremal euclidean line-sets. Proceedings of the London Mathematical Society 1997, 75(2):436–480. 10.1112/S0024611597000403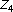 -linearity of Kerdock, Preparata, Goethals, and related codes. IEEE Transactions on Information Theory 1994, 40(2):301–319. 10.1109/18.312154
-linearity of Kerdock, Preparata, Goethals, and related codes. IEEE Transactions on Information Theory 1994, 40(2):301–319. 10.1109/18.312154