- Research Article
- Open access
- Published:
Characterization of Oblique Dual Frame Pairs
EURASIP Journal on Advances in Signal Processing volume 2006, Article number: 092674 (2006)
Abstract
Given a frame for a subspace of a Hilbert space
of a Hilbert space , we consider all possible families of oblique dual frame vectors on an appropriately chosen subspace
, we consider all possible families of oblique dual frame vectors on an appropriately chosen subspace . In place of the standard description, which involves computing the pseudoinverse of the frame operator, we develop an alternative characterization which in some cases can be computationally more efficient. We first treat the case of a general frame on an arbitrary Hilbert space, and then specialize the results to shift-invariant frames with multiple generators. In particular, we present explicit versions of our general conditions for the case of shift-invariant spaces with a single generator. The theory is also adapted to the standard frame setting in which the original and dual frames are defined on the same space.
. In place of the standard description, which involves computing the pseudoinverse of the frame operator, we develop an alternative characterization which in some cases can be computationally more efficient. We first treat the case of a general frame on an arbitrary Hilbert space, and then specialize the results to shift-invariant frames with multiple generators. In particular, we present explicit versions of our general conditions for the case of shift-invariant spaces with a single generator. The theory is also adapted to the standard frame setting in which the original and dual frames are defined on the same space.
References
Duffin RJ, Schaeffer AC: A class of nonharmonic Fourier series. Transactions of the American Mathematical Society 1952, 72: 341–366. 10.1090/S0002-9947-1952-0047179-6
Young RM: An Introduction to Nonharmonic Fourier Series. Academic Press, New York, NY, USA; 1980.
Daubechies I: Ten Lectures on Wavelets. SIAM, Philadelphia, Pa, USA; 1992.
Christensen O: An Introduction to Frames and Riesz Bases. Birkhäuser, Boston, Mass, USA; 2003.
Benedetto JJ: Irregular sampling and frames. In Wavelets: A Tutorial in Theory and Applications. Edited by: Chui CK. CRC Press, Boca Raton, Fla, USA; 1992:445–507.
Aldroubi A, Gröchenig K: Non-uniform sampling and reconstruction in shift-invariant spaces. Siam Review 2001, 43(4):585–620. 10.1137/S0036144501386986
Heil CE, Walnut DF: Continuous and discrete wavelet transforms. SIAM Review 1989, 31(4):628–666. 10.1137/1031129
Daubechies I: The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inform. Theory 1990, 36(5):961–1005. 10.1109/18.57199
Munch NJ: Noise reduction in tight Weyl-Heisenberg frames. IEEE Trans. Inform. Theory 1992, 38(2):608–616. 10.1109/18.119726
Eldar YC: Sampling with arbitrary sampling and reconstruction spaces and oblique dual frame vectors. Journal of Fourier Analysis and Applications 2003, 9(1):77–96. 10.1007/s00041-003-0004-2
Cvetković Z, Vetterli M: Overcomplete expansions and robustness. Proc. IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis (TFTS '96), June 1996, Paris, France 325–328.
Goyal VK, Vetterli M, Thao NT:Quantized overcomplete expansions in
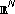 : analysis, synthesis, and algorithms. IEEE Trans. Inform. Theory 1998, 44(1):16–31. 10.1109/18.650985
: analysis, synthesis, and algorithms. IEEE Trans. Inform. Theory 1998, 44(1):16–31. 10.1109/18.650985Eldar YC, Bölcskei H: Geometrically uniform frames. IEEE Trans. Inform. Theory 2003, 49(4):993–1006. 10.1109/TIT.2003.809602
Cvetković Z: Overcomplete expansions for digital signal processing, M.S. thesis. University of California, Berkeley, Calif, USA; December 1995
Cvetković Z, Vetterli M: Oversampled filter banks. IEEE Trans. Signal Processing 1998, 46(5):1245–1255. 10.1109/78.668788
Bölcskei H: Oversampled filter banks and predictive subband coders, M.S. thesis. Vienna University of Technology, Vienna, Austria; November 1997
Bölcskei H, Hlawatsch F, Feichtinger HG: Frame-theoretic analysis of oversampled filter banks. IEEE Trans. Signal Processing 1998, 46(12):3256–3268. 10.1109/78.735301
Ferreira PJS: Mathematics for multimedia signal processing II—discrete finite frames and signal reconstruction. In Signal Processing for Multimedia. Edited by: Byrnes JS. IOS Press, Amsterdam, The Netherlands; 1999:35–54.
Eldar YC, Forney GD Jr.: Optimal tight frames and quantum measurement. IEEE Trans. Inform. Theory 2002, 48(3):599–610. 10.1109/18.985949
Eldar YC: Sampling without input constraints: Consistent reconstruction in arbitrary spaces. In Sampling, Wavelets and Tomography. Edited by: Benedetto JJ, Zayed AI. Birkhäuser, Boston, Mass, USA; 2004:33–60.
Werther T, Eldar YC: General framework for consistent sampling in Hilbert spaces. to appear in International Journal of Wavelets, Multiresolution and Information Processing
Christansen O, Eldar YC: Oblique dual frames and shift-invariant spaces. Applied and Computational Harmonic Analysis 2004, 17(1):48–68. 10.1016/j.acha.2003.12.003
Christansen O, Eldar YC: Generalized shift-invariant systems and frames for sub-spaces. submitted to Applied and Computational Harmonic Analysis
Li S, Ogawa H: Pseudoframes for subspaces with applications. Journal of Fourier Analysis and Applications 2004, 10(4):409–431. 10.1007/s00041-004-3039-0
Subbanna NK, Eldar YC: Efficient Gabor expansion using non minimal dual Gabor windows. Proc. 11th IEEE International Conference on Electronics, Circuits and Systems (ICECS '04), December 2004, Tel-Aviv, Israel 650–653.
Subbanna NK, Eldar YC: A fast algorithm for calculating the dual Gabor window with integer oversampling. Proc. 23rd IEEE Convention of Electrical and Electronics Engineers in Israel (IEEEI '04), September 2004, Tel-Aviv, Israel 368–371.
Werther T, Eldar YC, Subbana NK: Dual Gabor frames: theory and computational aspects. to appear in IEEE Trans. Signal Processing, October 2004
Heuser H: Functional Analysis. John Wiley & Sons, New York, NY, USA; 1982.
Tang W-S: Oblique projections, biorthogonal Riesz bases and multiwavelets in Hilbert space. Proceedings of the American Mathematical Society 2000, 128(2):463–473. 10.1090/S0002-9939-99-05075-3
Golub GH, Van Loan CF: Matrix Computations. 3rd edition. Johns Hopkins University Press, Baltimore, Md, USA; 1996.
Li S: On general frame decompositions. Numerical Functional Analysis and Optimization 1995, 16(9–10):1181–1191. 10.1080/01630569508816668
Christensen O, Deng B, Heil C: Density of Gabor frames. Applied and Computational Harmonic Analysis 1999, 7(3):292–304. 10.1006/acha.1999.0271
Benedetto J, Li S: The theory of multiresolution analysis frames and applications to filter banks. Applied and Computational Harmonic Analysis 1998, 5(4):389–427. 10.1006/acha.1997.0237
Unser M, Aldroubi A: A general sampling theory for nonideal acquisition devices. IEEE Trans. Signal Processing 1994, 42(11):2915–2925. 10.1109/78.330352
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Eldar, Y.C., Christensen, O. Characterization of Oblique Dual Frame Pairs. EURASIP J. Adv. Signal Process. 2006, 092674 (2006). https://doi.org/10.1155/ASP/2006/92674
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/ASP/2006/92674
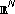 : analysis, synthesis, and algorithms. IEEE Trans. Inform. Theory 1998, 44(1):16–31. 10.1109/18.650985
: analysis, synthesis, and algorithms. IEEE Trans. Inform. Theory 1998, 44(1):16–31. 10.1109/18.650985