- Research Article
- Open access
- Published:
Sparse Representations Are Most Likely to Be the Sparsest Possible
EURASIP Journal on Advances in Signal Processing volume 2006, Article number: 096247 (2006)
Abstract
Given a signal and a full-rank matrix
and a full-rank matrix with
with , we define the signal's overcomplete representations as all
, we define the signal's overcomplete representations as all satisfying
satisfying . Among all the possible solutions, we have special interest in the sparsest one—the one minimizing
. Among all the possible solutions, we have special interest in the sparsest one—the one minimizing . Previous work has established that a representation is unique if it is sparse enough, requiring
. Previous work has established that a representation is unique if it is sparse enough, requiring . The measure
. The measure stands for the minimal number of columns from
stands for the minimal number of columns from that are linearly dependent. This bound is tight—examples can be constructed to show that with
that are linearly dependent. This bound is tight—examples can be constructed to show that with or more nonzero entries, uniqueness is violated. In this paper we study the behavior of overcomplete representations beyond the above bound. While tight from a worst-case standpoint, a probabilistic point of view leads to uniqueness of representations satisfying
or more nonzero entries, uniqueness is violated. In this paper we study the behavior of overcomplete representations beyond the above bound. While tight from a worst-case standpoint, a probabilistic point of view leads to uniqueness of representations satisfying . Furthermore, we show that even beyond this point, uniqueness can still be claimed with high confidence. This new result is important for the study of the average performance of pursuit algorithms—when trying to show an equivalence between the pursuit result and the ideal solution, one must also guarantee that the ideal result is indeed the sparsest.
. Furthermore, we show that even beyond this point, uniqueness can still be claimed with high confidence. This new result is important for the study of the average performance of pursuit algorithms—when trying to show an equivalence between the pursuit result and the ideal solution, one must also guarantee that the ideal result is indeed the sparsest.
References
Chen SS, Donoho DL, Saunders MA: Atomic decomposition by basis pursuit. SIAM Review 2001, 43(1):129–159. 10.1137/S003614450037906X
Natarajan BK: Sparse approximate solutions to linear systems. SIAM Journal on Computing 1995, 24(2):227–234. 10.1137/S0097539792240406
Davis G, Mallat SG, Avellaneda M: Adaptive greedy approximations. Constructive Approximations 1997, 13(1):57–98.
Mallat SG, Zhang Z: Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing 1993, 41(12):3397–3415. 10.1109/78.258082
Pati YC, Rezaiifar R, Krishnaprasad PS: Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition. Proceedings of 27th Asilomar Conference on Signals, Systems and Computers, November 1993, Pacific Grove, Calif, USA 1: 40–44.
Couvreur C, Bresler Y: On the optimality of the backward greedy algorithm for the subset selection problem. SIAM Journal on Matrix Analysis and Applications 2000, 21(3):797–808. 10.1137/S0895479898332928
Gilbert AC, Muthukrishnan S, Strauss MJ: Approximation of functions over redundant dictionaries using coherence. Proceedings of 14th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '03), January 2003, Baltimore, Md, USA 243–252.
Tropp JA, Gilbert AC, Muthukrishnan S, Strauss MJ: Improved sparse approximation over quasi-incoherent dictionaries. Proceedings of IEEE International Conference on Image Processing (ICIP '03), September 2003, Barcelona, Spain 1: 37–40.
Tropp JA: Greed is good: algorithmic results for sparse approximation. IEEE Transactions on Information Theory 2004, 50(10):2231–2242. 10.1109/TIT.2004.834793
Donoho DL, Elad M, Temlyakov VN: Stable recovery of sparse overcomplete representations in the presence of noise. to appear in IEEE Transactions on Information Theory, February 2004
Tropp JA: Just relax: Convex programming methods for subset selection and sparse approximation. In ICES Report 04-04. University of Texas at Austin, Austin, Tex, USA; February 2004.
Temlyakov VN:Greedy algorithms and
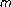 -term approximation with regard to redundant dictionaries. Journal of Approximation Theory 1999, 98(1):117–145. 10.1006/jath.1998.3265
-term approximation with regard to redundant dictionaries. Journal of Approximation Theory 1999, 98(1):117–145. 10.1006/jath.1998.3265Temlyakov VN: Weak greedy algorithms. Advances in Computational Mathematics 2000, 12(2–3):213–227.
Gorodnitsky IF, Rao BD: Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm. IEEE Transactions on Signal Processing 1997, 45(3):600–616. 10.1109/78.558475
Donoho DL, Huo X: Uncertainty principles and ideal atomic decomposition. IEEE Transactions on Information Theory 2001, 47(7):2845–2862. 10.1109/18.959265
Huo X: Sparse image representation via combined transforms, M.S. thesis. Stanford University, Stanford, Calif, USA; 1999.
Elad M, Bruckstein AM: A generalized uncertainty principle and sparse representation in pairs of bases. IEEE Transactions on Information Theory 2002, 48(9):2558–2567. 10.1109/TIT.2002.801410
Donoho DL, Elad M:Optimally sparse representation in general (non-orthogonal) dictionaries via
 minimization. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(5):2197–2202. 10.1073/pnas.0437847100
minimization. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(5):2197–2202. 10.1073/pnas.0437847100Gribonval R, Nielsen M: Sparse representations in unions of bases. IEEE Transactions on Information Theory 2003, 49(12):3320–3325. 10.1109/TIT.2003.820031
Fuchs J-J: On sparse representations in arbitrary redundant bases. IEEE Transactions on Information Theory 2004, 50(6):1341–1344. 10.1109/TIT.2004.828141
Candès EJ, Romberg J: Quantitative robust uncertainty principles and optimally sparse decompositions. to appear in Foundations of Computational Mathematics, 2004
Donoho DL:For most large underdetermined systems of linear equations the minimal
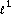 -norm solution is also the sparsest solution. In Tech. Rep. 2004-10. Department of Statistics, Stanford University, Stanford, Calif, USA; September 2004.
-norm solution is also the sparsest solution. In Tech. Rep. 2004-10. Department of Statistics, Stanford University, Stanford, Calif, USA; September 2004.Edelman A: Eigenvalues and condition numbers of random matrices. SIAM Journal on Matrix Analysis and Applications 1988, 9(4):543–560. 10.1137/0609045
Shen J: On the singular values of Gaussian random matrices. Linear Algebra and its Applications 2001, 326(1–3):1–14.
Strohmer T, Heath RW Jr.: Grassmannian frames with applications to coding and communication. Applied and Computational Harmonic Analysis 2003, 14(3):257–275. 10.1016/S1063-5203(03)00023-X
Tropp JA, Dhillon IS, Heath RW Jr., Strohmer T: Designing structured tight frames via an alternating projection method. IEEE Transactions on Information Theory 2005, 51(1):188–209.
Candès EJ, Donoho DL:New tight frames of curvelets and the problem of approximating piecewise
 images with piecewise
images with piecewise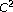 edges. 2002.
edges. 2002.Starck J-L, Candès EJ, Donoho DL: The curvelet transform for image denoising. IEEE Transactions on Image Processing 2002, 11(6):670–684. 10.1109/TIP.2002.1014998
Björner A: Some matroid inequalities. Discrete Mathematics 1980, 31(1):101–103. 10.1016/0012-365X(80)90179-X
Goldberg F: Overcomplete Bases, Spark, and Matroids. 2004.
Author information
Authors and Affiliations
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Elad, M. Sparse Representations Are Most Likely to Be the Sparsest Possible. EURASIP J. Adv. Signal Process. 2006, 096247 (2006). https://doi.org/10.1155/ASP/2006/96247
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/ASP/2006/96247
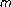 -term approximation with regard to redundant dictionaries. Journal of Approximation Theory 1999, 98(1):117–145. 10.1006/jath.1998.3265
-term approximation with regard to redundant dictionaries. Journal of Approximation Theory 1999, 98(1):117–145. 10.1006/jath.1998.3265 minimization. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(5):2197–2202. 10.1073/pnas.0437847100
minimization. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(5):2197–2202. 10.1073/pnas.0437847100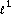 -norm solution is also the sparsest solution. In Tech. Rep. 2004-10. Department of Statistics, Stanford University, Stanford, Calif, USA; September 2004.
-norm solution is also the sparsest solution. In Tech. Rep. 2004-10. Department of Statistics, Stanford University, Stanford, Calif, USA; September 2004. images with piecewise
images with piecewise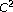 edges. 2002.
edges. 2002.