- Research Article
- Open access
- Published:
Quaternionic Lattice Structures for Four-Channel Paraunitary Filter Banks
EURASIP Journal on Advances in Signal Processing volume 2007, Article number: 037481 (2006)
Abstract
A novel approach to the design and implementation of four-channel paraunitary filter banks is presented. It utilizes hypercomplex number theory, which has not yet been employed in these areas. Namely, quaternion multipliers are presented as alternative paraunitary building blocks, which can be regarded as generalizations of Givens (planar) rotations. The corresponding quaternionic lattice structures maintain losslessness regardless of coefficient quantization and can be viewed as extensions of the classic two-band lattice developed by Vaidyanathan and Hoang. Moreover, the proposed approach enables a straightforward expression of the one-regularity conditions. They are stated in terms of the lattice coefficients, and thus can be easily satisfied even in finite-precision arithmetic.
References
Vaidyanathan PP, Doǧanata Z: The Role of lossless systems in modern digital signal processing: a tutorial. IEEE Transactions on Education 1989,32(3):181–197. 10.1109/13.34150
Vaidyanathan PP: Multirate Systems and Filter Banks. Prentice-Hall, Englewood Cliffs, NJ, USA; 1993.
Vaidyanathan PP, Nguyen TQ, Doǧanata Z, Saramaki T: Improved technique for design of perfect reconstruction FIR QMF banks with lossless polyphase matrices. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989,37(7):1042–1056. 10.1109/29.32282
Soman AK, Vaidyanathan PP, Nguyen TQ: Linear phase paraunitary filter banks: theory, factorizations and designs. IEEE Transactions on Signal Processing 1993,41(12):3480–3496. 10.1109/78.258087
Soman AK, Vaidyanathan PP: A complete factorization of paraunitary matrices with pairwise mirror-image symmetry in the frequency domain. IEEE Transactions on Signal Processing 1995,43(4):1002–1004. 10.1109/78.376855
Oraintara S, Tran TD, Heller PN, Nguyen TQ:Lattice structure for regular paraunitary linear-phase filterbanks and
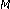 -band orthogonal symmetric wavelets. IEEE Transactions on Signal Processing 2001,49(11):2659–2672. 10.1109/78.960413
-band orthogonal symmetric wavelets. IEEE Transactions on Signal Processing 2001,49(11):2659–2672. 10.1109/78.960413Vaidyanathan PP, Hoang P-Q: Lattice structures for optimal design and robust implementation of two-band perfect reconstruction QMF banks. IEEE Transactions on Acoustic, Speech, and Signal Processing 1988,36(1):81–94. 10.1109/29.1491
Vaidyanathan PP: On coefficient-quantization and computational roundoff effects in lossless multirate filter banks. IEEE Transactions on Signal Processing 1991,39(4):1006–1008. 10.1109/78.80940
Chen Y-J, Amaratunga KS:
 -channel lifting factorization of perfect reconstruction filter banks and reversible
-channel lifting factorization of perfect reconstruction filter banks and reversible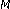 -band wavelet transforms. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing 2003,50(12):963–976. 10.1109/TCSII.2003.820233
-band wavelet transforms. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing 2003,50(12):963–976. 10.1109/TCSII.2003.820233Chen Y-J, Oraintara S, Amaratunga KS:Dyadic-based factorizations for regular paraunitary filterbanks and
 -band orthogonal wavelets with structural vanishing moments. IEEE Transactions on Signal Processing 2005,53(1):193–207.
-band orthogonal wavelets with structural vanishing moments. IEEE Transactions on Signal Processing 2005,53(1):193–207.Parfieniuk M, Petrovsky A: Quaternionic building block for paraunitary filter banks. Proceedings of the 12th European Signal Processing Conference (EUSIPCO '04), September 2004, Vienna, Austria 1237–1240.
Parfieniuk M, Petrovsky A: Quaternionic formulation of the first regularity for four-band paraunitary filter banks. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '06), May 2006, Kos, Greece 883–886.
Doǧanata Z, Vaidyanathan PP, Nguyen TQ: General synthesis procedures for FIR lossless transfer matrices, for perfect-reconstruction multirate filter bank applications. IEEE Transactions on Acoustics, Speech, and Signal Processing 1988,36(10):1561–1574. 10.1109/29.7544
Strang G, Nguyen TQ: Wavelets and Filter Banks. Wellesley-Cambridge Press, Wellesley, Mass, USA; 1996.
de Queiroz RL, Nguyen TQ, Rao KR: The GenLOT: generalized linear-phase lapped orthogonal transform. IEEE Transactions on Signal Processing 1996,44(3):497–507. 10.1109/78.489023
Gan L, Ma K-K: A simplified lattice factorization for linear-phase perfect reconstruction filter bank. IEEE Signal Processing Letters 2001,8(7):207–209. 10.1109/97.928679
Nguyen TQ, Vaidyanathan PP: Maximally decimated perfect-reconstruction FIR filter banks with pairwise mirror-image analysis (and synthesis) frequency responses. IEEE Transactions on Acoustics, Speech, and Signal Processing 1988,36(5):693–706. 10.1109/29.1579
Gan L, Ma K-K: A simplified lattice factorization for linear-phase paraunitary filter banks with pairwise mirror image frequency responses. IEEE Transactions on Circuits and Systems II: Express Briefs 2004,51(1):3–7. 10.1109/TCSII.2003.821515
Rioul O: Regular wavelets: a discrete-time approach. IEEE Transactions on Signal Processing 1993,41(12):3572–3579. 10.1109/78.258100
Steffen P, Heller PN, Gopinath RA, Burrus CS:Theory of regular
 -band wavelet bases. IEEE Transactions on Signal Processing 1993,41(12):3497–3511. 10.1109/78.258088
-band wavelet bases. IEEE Transactions on Signal Processing 1993,41(12):3497–3511. 10.1109/78.258088Hamilton WR: On quaternions; or on a new system of imaginaries in algebra. The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science 1844, 25: 489–495.
Kantor IL, Solodovnikov AS: Hypercomplex Numbers: An Elementary Introduction to Algebras. Springer, New York, NY, USA; 1989.
Baker A: Matrix Groups: An Introduction to Lie Group Theory. Springer, London, UK; 2002.
Baker HG: Quaternions and orthogonal 4x4 real matrices. June 1996.https://doi.org/www.gamedev.net/reference/articles/article428.asp
Salamin E: Application of quaternions to computation with rotations. Stanford AI Lab, Stanford, Calif, USA; 1979.
Howell TD, Lafon JC: The complexity of the quaternion product. In Tech. Rep. TR 75-245. Cornell University, Ithaca, NY, USA; June 1975. https://doi.org/citeseer.ist.psu.edu/howell75complexity.html
Parfieniuk M, Petrovsky A: Implementation perspectives of quaternionic component for paraunitary filter banks. Proceedings of the International Workshop on Spectral Methods and Multirate Signal Processing (SMMSP '04), September 2004, Vienna, Austria 151–158.
Parfieniuk M, Petrovsky A: Linear phase paraunitary filter banks based on quaternionic component. Proceedings of International Conference on Signals and Electronic Systems (ICSES '04), September 2004, Poznań, Poland 203–206.
Chen Y-J, Oraintara S, Tran TD, Amaratunga K, Nguyen TQ: Multiplierless approximation of transforms with adder constraint. IEEE Signal Processing Letters 2002,9(11):344–347. 10.1109/LSP.2002.804419
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Parfieniuk, M., Petrovsky, A. Quaternionic Lattice Structures for Four-Channel Paraunitary Filter Banks. EURASIP J. Adv. Signal Process. 2007, 037481 (2006). https://doi.org/10.1155/2007/37481
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/37481
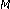 -band orthogonal symmetric wavelets. IEEE Transactions on Signal Processing 2001,49(11):2659–2672. 10.1109/78.960413
-band orthogonal symmetric wavelets. IEEE Transactions on Signal Processing 2001,49(11):2659–2672. 10.1109/78.960413 -channel lifting factorization of perfect reconstruction filter banks and reversible
-channel lifting factorization of perfect reconstruction filter banks and reversible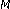 -band wavelet transforms. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing 2003,50(12):963–976. 10.1109/TCSII.2003.820233
-band wavelet transforms. IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing 2003,50(12):963–976. 10.1109/TCSII.2003.820233 -band orthogonal wavelets with structural vanishing moments. IEEE Transactions on Signal Processing 2005,53(1):193–207.
-band orthogonal wavelets with structural vanishing moments. IEEE Transactions on Signal Processing 2005,53(1):193–207. -band wavelet bases. IEEE Transactions on Signal Processing 1993,41(12):3497–3511. 10.1109/78.258088
-band wavelet bases. IEEE Transactions on Signal Processing 1993,41(12):3497–3511. 10.1109/78.258088