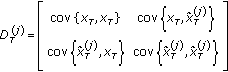Distributed Fusion Receding Horizon Filtering in Linear Stochastic Systems

Abstract

This paper presents a distributed receding horizon filtering algorithm for multisensor continuous-time linear stochastic systems. Distributed fusion with a weighted sum structure is applied to local receding horizon Kalman filters having different horizon lengths. The fusion estimate of the state of a dynamic system represents the optimal linear fusion by weighting matrices under the minimum mean square error criterion. The key contribution of this paper lies in the derivation of the differential equations for determining the error cross-covariances between the local receding horizon Kalman filters. The subsequent application of the proposed distributed filter to a linear dynamic system within a multisensor environment demonstrates its effectiveness.

1. Introduction

The concept of multisensor data fusion is the combination of data generated by a number of sensors in order to obtain more valuable data and perform inferences that may not be possible from a single sensor alone. This process has attracted growing interest for its potential applications in areas such as robotics, aerospace, and environmental monitoring, among others [1, 2].

In general, there are two fusion estimation methods commonly used to process the measured sensor data [3, 4]. If a central processor directly receives the measurement data of all local sensors and processes them in real time, the correlative result is known as the centralized estimation. However, this approach has some serious disadvantages, including bad reliability and survivability, as well as heavy communication and computational burdens.

The second method is called distributed estimation fusion, in which every local sensor is attached to a local processor. In this method, the processor optimally estimates a parameter or state of a system based on its own local measurements and transmits its local estimate to the fusion center where the received information is suitably associated to yield the global inference. The advantage of this approach is that the parallel structures would cause enlarge the input data rates and make easy fault detection and isolation [1–5]. Recently, various distributed and parallel versions of standard Kalman filters have been reported for linear dynamic systems within a multisensor environment [6–10].

To achieve a robust and accurate estimate of the state of a system under potential uncertainty, various techniques have been previously introduced and discussed. Among them, the receding horizon technique is popular and successful, due to its robustness against temporal uncertainty, and has been rigorously investigated. The receding horizon strategy was first introduced by Jazwinski, who labeled it as limited memory filtering [11]. The dynamic system without the process noise is believed to describe the efficiency of the idea through the maximum likelihood estimation scheme [11]. Following this, the optimal FIR filter for time-varying state-space models was suggested by W. H. Kwon et al. [12]. FIR filters make use of finite input and output measurements on the most recent time interval, called the receding horizon, or a horizon which is a moving, fixed-size estimation window. Because of the complicated structure of the FIR filter, a modified receding horizon Kalman FIR filter for linear continuous-time systems was proposed in [13]. As a general rule, the local receding horizon Kalman filters (LRHKFs) are typically more robust against dynamic model uncertainties and numerical errors than standard local Kalman filters, which utilize all measurements [14–17].

Distributed receding horizon fusion filtering for multiple sensors with equal horizon time intervals (horizon lengths) has also been proposed in [16]. In this case, all LRHKFs with the same horizon time interval, which are fused, utilize finite measurements over the most recent time interval [12–16].

In this paper, we consider the generalization of [16] for arbitrary, nonequal horizon lengths. Design of distributed filters for sensor measurements with nonequal horizon lengths is generally more complicated than for equal lengths due to a lack of common time intervals that contain all sensor data, making it impossible to design a centralized filtering algorithm. We propose using a distributed receding horizon filter for a set of local sensors with nonequal horizon lengths. Also, we derive the key differential equations for error cross-covariances between LRHKFs using different horizon lengths.

The remainder of this paper is organized as follows. The problem setting is described in Section 2. In Section 3, we present the main results pertaining to the distributed receding horizon filtering for a multisensor environment. Here, the key equations for cross-covariances between the local receding horizon filtering errors are derived. In Section 4, two examples for continuous-time dynamic systems within a multisensor environment illustrate the main results, and concluding remarks are then given in Section 5.

2. Problem Setting

Consider the linear continuous-time dynamic system with sensors:

(1)

(2)

where is the state, is the measurement, the system noise and the measurement noises , are uncorrelated white Gaussian noises with zero mean and intensity matrices and , respectively, and , , and are matrices with compatible dimensions. Also, the superscript denotes the th sensor, and is the total number of sensors.

The initial state , , is assumed to be Gaussian and uncorrelated with and ,

Our purpose, then, is to find the distributed fusion estimate of the state based on the overall horizon sensor measurements with different horizon time intervals , such that

(3)

3. Distributed Fusion Receding Horizon Filter

Now, we will show that the fusion formula (FF) [10, 17] is able to serve as the basis for designing a distributed fusion filter. A new distributed fusion receding horizon filter with nonequal horizon lengths(NE-DFRHF) includes two stages. In the first stage, LRHKFs (estimates) are computed and then linearly fused at the second stage based on the FF.

First step (Calculation of LRHKFs)

According to (1) and (2), we have local dynamic subsystems with the state vector and local (individual) sensor measurement :

(4)

where the number of a local subsystem is fixed.

Next, let us denote the local receding horizon estimate of the state based on the individual sensor measurements by . To determine we can apply the optimal receding horizon Kalman filter to subsystem (4) [12–15] to obtain the following differential equations:

(5)

with the horizon initial conditions:

(6)

determined by the Lyapunov equations [15] on the interval :

(7)

Thus, we obtain the LRHKFs with the corresponding local error covariances

Second step (Fusion of LRHKFs)

To express the final NE-DFRHF (estimate) for the state in terms of the LRHKFs , we use the FF. In this case,

(8)

where is the identity matrix, and are the time-varying weighted matrices determined by the mean square criterion.

Theorem 1 (see [10, 17]).

• (a) The optimal weights 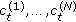satisfy the following linear algebraic equations:

  

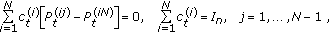  (9)

and they can be explicitly written in the following form:

(10)

where is the th submatrix of the block matrix ,

• (b) The fusion error covariance , is given by

  

  (11)

Therefore, (9)–(11), defining the unknown weights and fusion error covariance , depend on the local covariances , determined by (5), and the local cross-covariances

(12)

given in Theorem 2.

Theorem 2.

Without losing generality, let one assume that or . (a) The local cross-covariances (12) satisfy the following differential equations:

(13)

with the horizon initial conditions:

(14)

• (b) The covariance in (14) represents the nondiagonal element of the block covariance-matrix :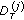

  

  (15)

at , described by the Lyapunov equation:

(16)

with the initial condition:

(17)

determined by (7).

The derivations of (13)–(17) are given in the appendix.

Thus, (5)–(17) completely define NE-DFRHF.

In the particular case of equal horizon lengths (, ), the local cross-covariances (12) satisfy the following differential equations:

(18)

with the horizon initial conditions and gains determined by (5)–(7), respectively.

Remark 3.

The LRHKFs , can be separated for different types of sensors. In other words, each local estimate can be found independently of the other estimates. Therefore, LRHKFs can be implemented in parallel for different sensors (2).

Remark 4.

Note, however, that the local error covariances , and the weights may be precomputed, since they do not depend on the sensor measurements (3), but rather on the noise statistics and and the system matrices , , and , which are the part of the system model (1), (2). Thus, once the measurement schedule has been settled, the real-time implementation of NE-DFRHF requires only the computation of the LRHKFs , and the final distributed fusion estimate .

4. Numerical Examples

In this section, two examples of continuous-time dynamic system with parametric model uncertainty are presented. In both cases, the local and final fusion estimates are biased. Nevertheless, these examples demonstrate the robustness of the proposed filter in terms of mean square error (MSE). The first example demonstrates the effectiveness of the distributed fusion receding horizon filter for different values of horizon lengths, and the second provides a comparison of the proposed filter with its nonreceding horizon version [17].

Example 5 (aircraft engine model).

Here, we verify NE-DFRHFs using a linearized model of an aircraft engine taken from [13]. The corresponding dynamic model is written as

(19)

where is an uncertain model parameter, and is a white Gaussian noise. The initial values are , and The system noise intensity is and the uncertainty is for the interval .

The second coordinate , related to the aircraft engine turbine temperature, is observable through a measurement model having three identical local sensors, one of which is the main sensor, while the others are reserve sensors. We have

(20)

where , are white Gaussian noises with intensities , .

The LRHKFs are designed for different receding horizon lengths of , and . The simulation results of the distributed fusion receding horizon filters with nonequal (NE-DFRHF) and equal (EQ-DFRHF) horizon lengths and LRHKF (LKF) are illustrated in Figures 1–4. All simulations were evaluated in terms of MSEs of 1000 Monte Carlo runs. Specifically, we focused on comparing the MSEs for the turbine temperature of the aircraft engine that directly contain the uncertainty in (19), such that

(21)

where , or .

Our point of interest is the behavior of the aforementioned filters, both inside and outside of the uncertainty interval . Since the uncertainty has little effect on the behavior of the filters (estimates) after the extremity of interval , for convenience of the MSE analysis, we introduce the extended time-interval , referred to as the Extended Uncertainty Interval (EUI). According to the simulation results, and .

Figure 1 compares the MSEs of NE-DFRHF ("NE") with three EQ-DFRHFs ("EQ") with common horizon lengths , .

From Figure 1 we can observe that inside the EUI, the NE-DFRHF is more accurate than the two EQ-DFRHFs with horizon lengths and . However, the NE-DFRHF is slightly worse than the EQ-DFRHF with horizon length , that is,

(22)

The reason for such a robust property (22) is to compensate for the given uncertainty , as the common horizon length for all local sensors (common memory of LRHKFs) should be minimal. In this case, it is equal, as .

Figure 2, on the other hand, shows that outside the EUI, the differences between the EQ-DFRHFs and NE-DFRHF are negligible. In this case, the EQ-DFRHF with the maximum common horizon length is more accurate than the NE-DFRHF, that is,

(23)

Figure 3 illustrates the time histories of the MSEs for NE-DFRHF and the LRHKFs (LKF). This figure shows that inside the EUI, the MSE of NE-DFRHF is better than that of LRHKFs with the horizon lengths and , but it is worse than the LRHKF with , that is,

(24)

Note, however, that outside the EUI the NE-DFRHF is better than all LRHKFs, as shown in Figure 4, that is,

(25)

It should also be noted that the reduction of the horizon length to zero inside the uncertainty interval is impossible due to the loss of sensor measurements (3). The problem in finding the optimal horizon length for each individual LRHKFs is quite complex.

Summarizing the simulation results provided in Figures 1–4, and using (22)–(25), we can conclude the following relations between MSEs inside/outside of the EUI:

(26)

Since, in actual situations, the uncertainty interval is unknown in advance, the MSEs relation (26) proves NE-DFRHF to be the best choice among the other filters.

Figure 1

MSEs comparison between NE-DFRHF and three EQ-DFRHFs inside the EUI.

Figure 2

MSEs comparison between NE-DFRHF and three EQ-DFRHFs before and after EUI. MSEs before EUIMSEs after EUI

Figure 3

MSEs comparison between NE-DFRHF and three LRHKFs inside the EUI.

Figure 4

MSEs comparison between NE-DFRHF and three LRHKFs before and after EUI. MSEs before EUIMSEs after EUI

Example 6 (water tank mixing system).

Consider a water tank system that accepts two different water temperatures, while simultaneously throws off the mixed water [18]. This system is described by

(27)

where , is the water level, is the water temperature, is the temperature of the sensor, and is a white Gaussian noise. The initial values are , and . Here, the system noise intensity is and the time-varying uncertain model parameter is on the interval :

(28)

The third coordinate , related to the sensor's temperature of the water tank, is observable through a measurement model containing three identical local sensors: one primary sensor, with two reserves. In this case, we have

(29)

where , , are white Gaussian noises with intensities ,

We now present a model to show the robustness of the receding horizon filter against uncertainty [13]. In this example, we demonstrate the advantage of the receding horizon strategy using two filters: a distributed fusion receding horizon filter (see Section 3) and a distributed nonreceding horizon fusion filter (DNF) [17]. Three EQ-DFRHFs were designed for the different common horizon lengths , and . We focus on the MSEs of the third coordinate , called the sensor temperature, because the time-varying uncertainty from (27) appears only in this coordinate:

(30)

where or .

Figure 5 compares the MSEs of the EQ-DFRHFs ("EQ") for the horizon lengths of and . As can be observed in this figure, inside the time-interval , referred to as the Uncertainty Interval (UI), all EQ-DFRHFs demonstrate better performance than DNF; this is in general agreement with the robustness of the receding horizon strategy. The MSEs of the nonreceding horizon filter DNF are remarkably larger than other EQ-DFRHFs. Also, the EQ-DFRHF with a horizon length is more accurate than the EQ-DFRHFs with horizon lengths and , that is,

(31)

On the other hand, outside the UI the differences between the EQ-DFRHFs are negligible, though the EQ-DFRHF with a maximum common horizon length of is more accurate than other EQ-DFRHFs, that is,

(32)

Summarizing the simulation results in Figure 5, EQ-DFRHF has a parallel structure and allows parallel processing of observations, thereby making it more reliable than the others since the remaining faultless sensors can continue the fusion estimation if some sensors become faulty. Moreover, EQ-DFRHF can produce high-quality results in a real-time processing environment.

Figure 5

MSEs comparison between DNF and three EQ-DFRHFs.

5. Conclusions

In this paper, we proposed a new distributed receding horizon filter for a set of local sensors with nonequal horizon lengths. Also, we derived the key differential equations for determining the local cross-covariances between LRHKFs with the different horizon lengths.

Furthermore, it was found that NE-DFRHF can complement for robustness and accuracy when a common time interval containing all sensor data is lacking. Subsequent simulation results and comparisons between NE-DFRHF and other EQ-DFRHFs and LRHKFs verify the estimation accuracy and robustness of the proposed filter.

Appendix

Derivation of (13)–(17)

Local filtering errors and , satisfy the following equations:

(A.1)

Next, without losing generality, let us assume that

(A.2)

Then, on the common time-interval , (A.1) can be rewritten in the following form:

(A.3)

with the special horizon initial conditions:

(A.4)

Application of the Lyapunov equation to the model (A.3) yields the following differential equation for the cross-covariance on the common time-interval:

(A.5)

Substituting the matrices , and into (A.5), we obtain the following equation for the cross-covariance :

(A.6)

with the initial condition:

(A.7)

To determine the covariance in (A.7), let us consider a set of stochastic equations for the state and its estimate on the remain time-interval . From (1) and (5) we obtain

(A.8)

with the initial condition:

(A.9)

where is a white Gaussian noise with intensity matrix

Then, the covariance of vector

(A.10)

is described by the Lyapunov equation for the model (A.8):

(A.11)

Since the second component of the initial vector is nonrandom , the structure of the initial covariance can then take the special form:

(A.12)

where the nonzero element in (A.7) and (A.12) represents the covariance of the state , which is determined by the Lyapunov equation (7).

This completes the proof of Theorem 2.