- Research Article
- Open access
- Published:
A WiMAX-Based Implementation of Network MIMO for Indoor Wireless Systems
EURASIP Journal on Advances in Signal Processing volume 2009, Article number: 963547 (2009)
Abstract
It is well known that multiple-input multiple-output (MIMO) techniques can bring numerous benefits, such as higher spectral efficiency, to point-to-point wireless links. More recently, there has been interest in extending MIMO concepts to multiuser wireless systems. Our focus in this paper is on network MIMO, a family of techniques whereby each end user in a wireless access network is served through several access points within its range of influence. By tightly coordinating the transmission and reception of signals at multiple access points, network MIMO can transcend the limits on spectral efficiency imposed by cochannel interference. Taking prior information-theoretic analyses of network MIMO to the next level, we quantify the spectral efficiency gains obtainable under realistic propagation and operational conditions in a typical indoor deployment. Our study relies on detailed simulations and, for specificity, is conducted largely within the physical-layer framework of the IEEE 802.16e Mobile WiMAX system. Furthermore, to facilitate the coordination between access points, we assume that a high-capacity local area network, such as Gigabit Ethernet, connects all the access points. Our results confirm that network MIMO stands to provide a multiple-fold increase in spectral efficiency under these conditions.
1. Introduction
The initial cellular systems deployed in the 1980's and 1990's featured conservative frequency reuse patterns in order to ensure a high signal-to-interference-and-noise ratio (SINR) on individual links. This allowed the links to operate with limited signal processing, at the expense of having a small number of concurrent links. Altogether the resulting system spectral efficiency was low and soon became insufficient, given the rise in demand for wireless services.
Since then, the introduction of advanced techniques like powerful forward error correction, fast power control, link adaptation, incremental redundancy, and so forth, has progressively improved the spectral efficiency at the link-level. Furthermore, such high efficiencies have become feasible at diminishing SINRs, thereby enabling ever more aggressive frequency reuse patterns. In fact, emerging systems (e.g., 3GPP Long-Term Evolution [1] and IEEE 802.16 WiMAX [2]) are already reaching the point of universal frequency reuse and are therefore limited first and foremost by their own interference.
With link efficiencies nearing capacity and with universal frequency reuse, this marks the end of the road for the approach followed thus far to improve the system spectral efficiency. In recent years, the introduction of multiple-input multiple-output (MIMO) techniques has provided powerful new means for enhancing wireless system performance in many ways (chiefly in terms of spectral efficiency). MIMO techniques enable frequency reusewithin each cell but are still subject to the high levels of interference from other cells. It is becoming increasingly clear that, MIMO schemes notwithstanding, major improvements in spectral efficiency will require addressing intercell interference more directly.
Traditionally, in cellular systems each user is assigned to an access point (AP) on the basis of criteria like signal strength. The user then communicates with that serving AP while causing interference to users served by all other APs. A key observation here is that, in the uplink specifically, intercell interference is merely a superposition of signals that were intended for other APs, that is, that have been collected at the wrong place. If these signals could be properly classified and routed, they would in fact cease to be interference and become useful in the detection of the information they bear. (A dual observation can be made about the downlink.)
While challenging, this is theoretically possible by virtue of the fact that the APs are connected to a common backhaul network (usually wired). This is tantamount to recognizing, in information-theoretic parlance, that a cellular uplink is not an interference channel but rather a multiaccess channel with distributed receiving antennas, and that it should be operated as such: all users should be served through all the APs within their range of influence. Similarly, the downlink should be operated as a broadcast channel with distributed transmitting antennas. This ambitious approach, which we term "network MIMO'', exploits the much higher bandwidth that can be made available in the wired backhaul network to transcend intercell interference and alleviate the wireless bottleneck. We note that network MIMO is also referred to by other names in literature, such as macrodiversity, multicell MIMO/processing, and base station cooperation/coordination.
Early information-theoretic results hinting at the network MIMO concept for the uplink can be found in [3]. For reasons of analytical tractability, a highly simplified cellular system model is proposed in [3], wherein cochannel interference arises only from adjacent cells and its power is characterized by a single parameter (distance-based power loss and shadow fading effects are ignored). Within the context of this simplified model (thereafter referred to as the Wyner model), the throughputs achievable with both optimal and linear minimum mean squared error (MMSE) joint processing of the received signals at all access points are derived for nonfading channels (also see [4] for related work). These results are extended to fading channels in [5]. Analogous results for the downlink (also for a system based on the Wyner model) are in [6], where a simple joint linear precoding scheme combined with dirty paper coding is analyzed. Emphasis is placed in these papers on the large-network limit, where the numbers of access points and users both go to infinity.
In [7], multicell zero-forcing beamforming on the downlink is studied (again within the Wyner system model), with a sum power constraint across all access points. Sum rate expressions for several joint linear precoding schemes on the downlink can be found in [8], for nonfading channels. In [9], a variant of the Wyner cellular model is introduced, and the average per-cell sum rates on downlink and uplink are analyzed. Uplink network MIMO for code division multiple access (CDMA) systems with random spreading and chip-level interleaving is studied in [10]. Further, the impact of finite-capacity backhaul links between the access points on network MIMO gains (for the Wyner model) has been quantified in [11–13].
The emphasis in the above papers (and others referenced therein) is on deriving rigorous analytical results relating to network MIMO, using the tools of information theory, which could then provide insight into the role played by key system parameters. However, as pointed out above, these results are derived for rather unrealistic models of cellular systems. A complementary body of work on network MIMO focuses on the performance evaluation of specific system architectures and signal processing techniques, usually by numerical simulation, with more realistic models for signal propagation and cochannel interference (accounting, at least, for distance-based power loss and shadow fading effects).
A proposal for a future-generation cellular system architecture based on joint processing of uplink and downlink signals by clusters of base stations can be found in [14]. The potential for cochannel interference mitigation through such joint processing is explored from a practical signal-processing standpoint in [15]. In [16–18], network MIMO on the downlink is studied, with the goal of achieving fairness between users by maximizing the minimum user rate, subject to per-base-station power constraints. Analogous uplink results can be found in [19, 20], where the impact of limited coordination clusters is also quantified. Related work on downlink network MIMO with limited clusters can be found in [21]. In [22], the problem of linear transceiver design for downlink network MIMO with per-base-station power constraints is studied, with various criteria based on minimizing mean squared error. Distributed implementations of uplink and downlink network MIMO based on local message passing are proposed in [23, 24] (related work can be found in [25]). See [26] for an overview of several approaches to handling interference in cellular systems, including network MIMO.
The aforementioned studies have shown that network MIMO indeed holds the promise of very large increases in spectral efficiency. However, these findings have relied on very basic channel models (e.g., frequency-selective fading has not been considered), and on the assumption that all relevant channel state information is instantaneously and perfectly available at each AP and user. Also, ideal Shannon-rate coding has been assumed, that is, the impact of real-world coding and modulation schemes has not been evaluated.
The objective of this paper is therefore to take the evaluation of network MIMO to the next level, assessing its viability and quantifying its spectral efficiency gain under more realistic conditions. To that end, and for the sake of specificity, we frame our study within the context of the IEEE 802.16e Mobile WiMAX system [2]. Mobile WiMAX is expected to be widely deployed and, with its time-division duplexing (TDD) format and resulting uplink-downlink reciprocity, is particularly well suited to accommodate network MIMO. To further facilitate the coordination between APs, for this initial study we postulate an indoor deployment organized around a high-speed local area network (LAN) backhaul, for example, Gigabit Ethernet [27]. Although systems designed specifically for indoor environments exist (e.g., IEEE 802.11), they do not have an efficient medium access control (MAC) layer. Moreover, a Mobile-WiMAX-based network MIMO system can be migrated to an outdoor environment more readily. A sophisticated indoor WiMAX simulator has therefore been built which replicates all the relevant functionalities including coding and decoding, modulation and demodulation, pilot insertion, channel estimation, linear precoding, power control, link adaptation, and so forth. System throughput results from this simulator show that, even under realistic operational conditions, network MIMO can provide a multifold increase in spectral efficiency on both uplink (user-to-AP) and downlink (AP-to-user).
Other papers address similar practical issues relating to network MIMO in real-world systems. In [28, 29], capacity estimates derived from channel measurements in an urban microcellular system are used to demonstrate that network MIMO can provide a large gain in spectral efficiency through cochannel interference mitigation. Synchronization techniques required to enable base station cooperation (e.g., frequency offset correction) are dealt with in [30]. A hardware-based testbed for evaluating network MIMO algorithms in real-world conditions is described in [31]. In [32], it is argued that interference in cellular systems is fundamentally asynchronous in nature, and the impact of this asynchronicity on network MIMO is analyzed. Finally, in [33], a combination of antenna tilting, interference avoidance, and interference suppression through base station cooperation is proposed to increase spectral efficiency.
To the best of our knowledge, however, network MIMO has not been evaluated before over a real-world air interface with practical coding and modulation, link adaptation through rate and power control, and so forth, and with imperfect channel state information (obtained by explicit pilot-symbol-aided estimation). This is our goal in this paper.
The rest of the paper is organized as follows. Section 2 contains some background material on the WiMAX specification, and Section 3 the system model implemented in our network MIMO simulator. In Section 4, we describe all relevant algorithms. Section 5 contains the numerical results. Our conclusions are in Section 6.
2. Relevant WiMAX Details
Mobile WiMAX is an air interface specification based on orthogonal frequency division multiplexing (OFDM). It supports a wide range of system configurations, with multiple options for channel bandwidth, frame duration, time-frequency resource partitioning, and so forth. In this section, we highlight some of the specific choices for these parameters made in our simulator. Further details of the WiMAX standard can be found in [2].
We consider a 10 MHz channel, split equally between uplink and downlink using TDD, with the generic frame structure shown in Figure 1. WiMAX defines several "permutations'', or ways of partitioning the time-frequency resource into subchannels, each with its own arrangement of pilot symbols for enabling channel estimation. For our purposes, we use the so-called AMC  permutation which is well suited for low-mobility indoor environments (AMC stands for Adaptive Modulation and Coding). It has a lower pilot overhead (1 out of every 9 symbols) than other permutations and has the further attractive feature of being identical on the uplink and downlink.
permutation which is well suited for low-mobility indoor environments (AMC stands for Adaptive Modulation and Coding). It has a lower pilot overhead (1 out of every 9 symbols) than other permutations and has the further attractive feature of being identical on the uplink and downlink.
For a 10 MHz channel, the Fast Fourier Transform (FFT) size in the AMC  permutation is 1024, with the subcarrier spacing being 10.9375 kHz. The cyclic prefix consists of 128 samples, which provides immunity to delay spreads up to 11.4
permutation is 1024, with the subcarrier spacing being 10.9375 kHz. The cyclic prefix consists of 128 samples, which provides immunity to delay spreads up to 11.4  (this is clearly an overkill for typical indoor environments, but it keeps the door open for migration to outdoor macrocellular deployments). A total of 864 subcarriers are modulated, 768 by data symbols and 96 by pilot symbols. The basic resource allocation unit, or "slot'', is a rectangle of 2 frequency bins (each bin being comprised of 8 data subcarriers and 1 pilot subcarrier) by 3 OFDM symbols, hence the
(this is clearly an overkill for typical indoor environments, but it keeps the door open for migration to outdoor macrocellular deployments). A total of 864 subcarriers are modulated, 768 by data symbols and 96 by pilot symbols. The basic resource allocation unit, or "slot'', is a rectangle of 2 frequency bins (each bin being comprised of 8 data subcarriers and 1 pilot subcarrier) by 3 OFDM symbols, hence the  in the name. The arrangement of data and pilot tones within each slot is shown in Figure 1.
in the name. The arrangement of data and pilot tones within each slot is shown in Figure 1.
We take the frame duration to be 5 ms, with each frame having 24 downlink and 24 uplink OFDM symbols, separated by equal-duration guard intervals (approximately 31  each). We note that control channels are not considered in the frame structure because they will have the same impact on overhead for both conventional and network MIMO modes.
each). We note that control channels are not considered in the frame structure because they will have the same impact on overhead for both conventional and network MIMO modes.
The tile structure, uplink sounding symbols, and downlink pilot symbols are used for channel estimation and will be described further in Section 4.1.
3. System Model
For our simulation study, we posit a cuboidal indoor area of width 80 m, length 10 m, and height 3 m, with 8 APs arranged in a straight line at 10 m spacing along the ceiling, as shown in Figure 2. These APs serve 8 users, and we assume that all users/APs transmit simultaneously in every uplink/downlink frame. The APs and users are each equipped with a single antenna. Note that we do not assume a wrapped-around network; so users close to the edge of the network will experience less interference than those near the middle. This will only tend to lower the spectral efficiency gain achievable with network MIMO.
For the conventional system (no network MIMO), we consider both universal frequency reuse and frequency reuse  . (As we will see in Section 5, the downlink SINR distribution under universal reuse results in a significant fraction of users falling below the SINR required to achieve the minimum rate. We consider frequency reuse
. (As we will see in Section 5, the downlink SINR distribution under universal reuse results in a significant fraction of users falling below the SINR required to achieve the minimum rate. We consider frequency reuse  because it improves the SINR distribution so that fewer users are below this critical SINR value.) Under full frequency reuse, all users and APs transmit over the entire time-frequency grid. Under frequency reuse
because it improves the SINR distribution so that fewer users are below this critical SINR value.) Under full frequency reuse, all users and APs transmit over the entire time-frequency grid. Under frequency reuse  , the 10 MHz bandwidth is partitioned equally into upper and lower 5 MHz subbands and APs are sequentially assigned to each subband in alternating fashion. Under frequency reuse 1/2, the number of cochannel AP (or user) interferers on the downlink (or uplink) is reduced from 7 to 3 compared to full reuse, resulting in an improvement in the lower-tail SINR distribution.
, the 10 MHz bandwidth is partitioned equally into upper and lower 5 MHz subbands and APs are sequentially assigned to each subband in alternating fashion. Under frequency reuse 1/2, the number of cochannel AP (or user) interferers on the downlink (or uplink) is reduced from 7 to 3 compared to full reuse, resulting in an improvement in the lower-tail SINR distribution.
For generality, we denote the number of cochannel APs by  , and the total number of users they serve by
, and the total number of users they serve by  . While we always assume
. While we always assume  , it is useful to assign different variables for the sake of clarity. For the full reuse case,
, it is useful to assign different variables for the sake of clarity. For the full reuse case,  , while for frequency reuse
, while for frequency reuse  ,
,  . On the uplink, we let
. On the uplink, we let  denote the baseband signal received by the
denote the baseband signal received by the  th AP
th AP  over time-frequency data symbol
over time-frequency data symbol  . Stacking the received signals of the
. Stacking the received signals of the  APs, we can model the received signal vector
APs, we can model the received signal vector  as
as

where  is the channel matrix whose
is the channel matrix whose  th element, denoted as
th element, denoted as  , is the complex channel coefficient between the
, is the complex channel coefficient between the  th user and the
th user and the  th AP,
th AP,  is the transmitted complex baseband signal whose
is the transmitted complex baseband signal whose  th element is transmitted by the
th element is transmitted by the  th user, and
th user, and  is the circularly symmetric complex Gaussian additive noise at the AP receivers, with
is the circularly symmetric complex Gaussian additive noise at the AP receivers, with  and
and  . The transmit power of the
. The transmit power of the  th user is
th user is  , and the power for all users is limited by the maximum uplink transmit power:
, and the power for all users is limited by the maximum uplink transmit power:  . Users transmit independently so the transmit covariance
. Users transmit independently so the transmit covariance  can be written as a diagonal matrix
can be written as a diagonal matrix

We assume that the users and APs are assigned so that the  th indexed user is assigned to the
th indexed user is assigned to the  th indexed AP.
th indexed AP.
For the downlink system model, we will use a nearly identical notation, but it will be clear whether we are discussing the uplink or downlink based on the context. We let  denote the baseband signal received by the
denote the baseband signal received by the  th user
th user  over time-frequency data symbol
over time-frequency data symbol  . Stacking the received signals of the
. Stacking the received signals of the  users, we can model the received signal vector
users, we can model the received signal vector  as
as

where, using the same notation as for the uplink channel,  is the channel matrix whose
is the channel matrix whose  th element, denoted as
th element, denoted as  , is the complex channel coefficient between the
, is the complex channel coefficient between the  th user and the
th user and the  th AP. The vector
th AP. The vector  is the transmitted complex baseband signal across the APs, whose
is the transmitted complex baseband signal across the APs, whose  th element is transmitted by the
th element is transmitted by the  th AP. The vector
th AP. The vector  is the circularly symmetric complex Gaussian additive noise at the users' receivers, with
is the circularly symmetric complex Gaussian additive noise at the users' receivers, with  , and
, and  . The transmit power of the
. The transmit power of the  th antenna is
th antenna is  , and the power for each antenna is limited by the maximum downlink transmit power:
, and the power for each antenna is limited by the maximum downlink transmit power:  .
.
Each channel coefficient  captures the effects of fading, shadowing, and pathloss over time-frequency symbol
captures the effects of fading, shadowing, and pathloss over time-frequency symbol  between the
between the  th AP and
th AP and  th user. Specifically,
th user. Specifically,

where  is a zero-mean circularly symmetric complex Gaussian random variable with unit variance which represents the effects of frequency-dependent small-scale fading,
is a zero-mean circularly symmetric complex Gaussian random variable with unit variance which represents the effects of frequency-dependent small-scale fading,  is the distance between user
is the distance between user  and AP
and AP  ,
,  is the path loss exponent,
is the path loss exponent,  is the lognormal shadowing between user
is the lognormal shadowing between user  and AP
and AP  , and
, and  is the channel gain at a reference distance
is the channel gain at a reference distance  . In other words, if there is no fading (
. In other words, if there is no fading ( ) and
) and  , then
, then  . We refer to the parameter
. We refer to the parameter  as the reference signal-to-noise ratio (SNR).
as the reference signal-to-noise ratio (SNR).
Signal propagation is based on channel model B from 802.11n [34], which specifies a path loss exponent  of 2 up to 5 m and 3.5 beyond, and shadow fading standard deviation of 3 dB up to 5 m and 4 dB beyond. There is no spatial correlation across APs or users; so the fading coefficients
of 2 up to 5 m and 3.5 beyond, and shadow fading standard deviation of 3 dB up to 5 m and 4 dB beyond. There is no spatial correlation across APs or users; so the fading coefficients  are independent across the AP and user indices. However, fading is correlated in time and frequency; the power-delay profile is detailed in Table 1 while the Doppler spectrum is Clarke-Jakes with a maximum frequency of 10 Hz.
are independent across the AP and user indices. However, fading is correlated in time and frequency; the power-delay profile is detailed in Table 1 while the Doppler spectrum is Clarke-Jakes with a maximum frequency of 10 Hz.
We measure the uplink and downlink throughput of users randomly distributed in the network by averaging over multiple simulation trials. For a given trial, we sequentially generate random user locations with a uniform distribution on the floor of the network area and shadow fading realizations for the links to all the APs. We assign a user to the AP with maximum average SNR, accounting for distance-based path loss and shadowing. Users whose maximum-SNR AP has already been chosen by a previously generated user are simply discarded. We continue dropping users until all APs are assigned one user. For the received signal models given by (1) and (3), we assume the APs and users are indexed so that the  th AP is assigned to the
th AP is assigned to the  th user.
th user.
4. Algorithms
The objective of the simulations is to compare the user rate distributions, with and without network MIMO, in the indoor WiMAX system of interest. In this section, we describe the algorithms implemented in the simulator to facilitate this comparison.
In principle, we could define arbitrary coordination clusters of APs, with each such cluster performing joint coherent processing of the signals to/from some subset of users. However, for simplicity, we shall consider only two extreme cases: full coordination between all the APs (i.e., all the APs are in a single coordination cluster) and no coordination between the APs (i.e., each AP constitutes a coordination cluster by itself). We refer to these cases, respectively, as network MIMO and conventional.
Channel estimation is performed using algorithms described in Section 4.1. The transceiver algorithms for the uplink and downlink are given, respectively, in Sections 4.2 and 4.3. Transmission rates and powers are set using algorithms described in Section 4.4.
4.1. Channel Estimation
For the purposes of uplink network MIMO, it is essential to be able to allocate the same time-frequency resources to multiple users who might interfere strongly with each other, such users then being separated by spatial processing across several APs. In order for the APs to estimate the channels of all such users, it must be possible to distinguish between the pilots transmitted by them in some dimension (e.g., time, frequency, or code). However the default per-slot pilots provided in the AMC permutation do not have this property; that is, users who are assigned the same time-frequency resource by different APs do not have distinguishable pilots. The assumption in WiMAX seems to be that interference avoidance through fractional frequency reuse will preclude a situation where users who are likely to interfere strongly with each other share the same time-frequency resources.
There is, however, a workaround in the form of the uplink sounding feature in 802.16e, which allows the transmission of noninterfering pilots on the uplink from all user antennas. For our purposes, we assume that 3 OFDM symbols (1st, 14th, and 24th) in each uplink subframe are reserved for the transmission of sounding pilots. In each of these OFDM symbols, pilot symbols from different user antennas are interleaved in the subcarrier dimension, for example, user antenna  transmits pilot symbols on subcarriers
transmits pilot symbols on subcarriers  , and so forth. Thus the pilots from different user antennas are separated in frequency. Note that using the uplink sounding symbols doubles the overall pilot symbol overhead from
, and so forth. Thus the pilots from different user antennas are separated in frequency. Note that using the uplink sounding symbols doubles the overall pilot symbol overhead from  to
to  , since the per-slot pilot locations cannot be converted to data locations.
, since the per-slot pilot locations cannot be converted to data locations.
On the uplink, channel estimation for each user is performed at each AP on a frame-by-frame basis, with no memory across frames. The sounding pilot symbols allow the direct estimation of each user's channel on every eighth subcarrier during the 1st, 14th, and 24th OFDM symbols of each uplink subframe. The channel at other time-frequency locations can then be estimated by two-dimensional interpolation. We compared simple linear interpolation with minimum mean squared error (MMSE) interpolation (see, e.g., [35, Chapter 5]). The latter is potentially more accurate, but requires the estimation and tracking of the time-frequency covariance structure of the channel, and is therefore potentially less robust. For the indoor system parameters considered, the performance of the two techniques was nearly identical. We therefore present results only for linear interpolation.
Once uplink channel estimates are available for all time-frequency locations, the APs must compute beamforming weights for the users. In principle, these beamforming weights could be computed individually for every time-frequency location. However, this entails excessive computation. It is therefore expedient to average the channel estimates over a block of contiguous time-frequency locations (over which the channel can be expected not to vary significantly), and to compute a single set of beamforming weights for all those locations.
We will use the term tiles to refer to the contiguous time-frequency locations over which the channel estimates are averaged (and then used to compute a single set of beamforming weights for the users). For the indoor channel of interest to us, a reasonable choice of the tile size is 18 contiguous subcarriers (i.e., 1 frequency "bin'') by 24 OFDM symbols (i.e., the entire duration of an uplink subframe).
Exploiting TDD channel reciprocity, the uplink channel estimates are subsequently used to compute the downlink transmitter weights for network MIMO, as described in Section 4.3. (In practice, even with TDD, reciprocity will require the calibration of hardware at both ends of the link.) These weights, calculated once for each tile, form nominally orthogonal beams among the  users for modulating both data and pilot symbols.
users for modulating both data and pilot symbols.
For both uplink and downlink, we let  denote the MIMO channel estimate for the
denote the MIMO channel estimate for the  th time-frequency symbol, where the
th time-frequency symbol, where the  th element
th element  is the estimate between the
is the estimate between the  th AP and
th AP and  th user. Since channel estimates are computed per tile, estimates with indices
th user. Since channel estimates are computed per tile, estimates with indices  belonging to the same tile are identical.
belonging to the same tile are identical.
4.2. Uplink Transceiver
For the conventional transceiver, each user is detected with a matched filter receiver at the assigned AP with maximum average SNR. The user/AP indexing is such that the  th user is assigned to the
th user is assigned to the  th AP. Given the channel estimate for the
th AP. Given the channel estimate for the  th user at the
th user at the  th AP
th AP  and the received signal at the
and the received signal at the  th AP
th AP  given by the
given by the  th element of the vector (1), the matched filter output for the
th element of the vector (1), the matched filter output for the  th user is given by
th user is given by  .
.
In order to perform rate control as described in Section 4.4, an estimate of the SINR must be computed, assuming that the channel estimates and actual channel coefficients are equivalent, and that the thermal noise variance  is known. The SINR at the output of the matched filter for user
is known. The SINR at the output of the matched filter for user  over symbol
over symbol  is given by
is given by

Under network MIMO, the users' signals are jointly detected using a linear MMSE receiver spanning all AP antennas. The  -dimensional MMSE output across the APs over symbol
-dimensional MMSE output across the APs over symbol  is
is

For the purposes of rate control, the SINR at the output of the MMSE receiver for user  over symbol
over symbol  as a function of the transmit powers
as a function of the transmit powers  is
is

4.3. Downlink Transceiver
As in the uplink, the receiver for conventional downlink transmission with no AP coordination is the matched filter. In this case, the  th user is assigned to the
th user is assigned to the  th AP. Given the channel estimate for the
th AP. Given the channel estimate for the  th AP at the
th AP at the  th user
th user  and the received signal by the
and the received signal by the  th user
th user  given by the
given by the  th element of the vector (3), the matched filter output for this user is given by
th element of the vector (3), the matched filter output for this user is given by  .
.
The SINR at the output of the matched filter for user  over symbol
over symbol  is given by
is given by

For downlink network MIMO, zero-forcing (ZF) beamforming is applied jointly across the APs [36]. By applying ZF beamforming across  transmit antennas, up to
transmit antennas, up to  users can receive data over mutually orthogonal beams under the assumption of ideal channel knowledge at both the transmitter and receiver and sufficient spatial separation of the users. In the simulation, because the channel knowledge at both transmitter and receiver is not ideal, each user will experience some residual interference. Under the zero-forcing criterion, the transmitted signal vector in (3) is given by
users can receive data over mutually orthogonal beams under the assumption of ideal channel knowledge at both the transmitter and receiver and sufficient spatial separation of the users. In the simulation, because the channel knowledge at both transmitter and receiver is not ideal, each user will experience some residual interference. Under the zero-forcing criterion, the transmitted signal vector in (3) is given by

where  is the data symbol vector for the
is the data symbol vector for the  users. Therefore, if the channel estimation is ideal (
users. Therefore, if the channel estimation is ideal ( ), the received signal by each user is simply its desired data symbol plus additive noise:
), the received signal by each user is simply its desired data symbol plus additive noise:

Defining  to be the
to be the  precoding matrix, and defining
precoding matrix, and defining  to be the power allocated to the
to be the power allocated to the  th user, the power transmitted by the
th user, the power transmitted by the  th AP is
th AP is

The resulting SINR for user  is
is

and the maximum achievable rate is  . For the purposes of rate control, the powers
. For the purposes of rate control, the powers  for
for  are computed in order to maximize the sum rate and such that each antenna is subject to a power constraint:
are computed in order to maximize the sum rate and such that each antenna is subject to a power constraint:

The problem defined in (13) is a convex optimization that can be solved numerically using conventional interior point methods [37, 38].
4.4. Rate and Power Control
Turbo coding at code rates of  and
and  is used in conjunction with 4QAM, 16QAM, and 64QAM constellations. To support users in low SINR conditions, repetition of code bits is allowed (to build up SINR) in the rate
is used in conjunction with 4QAM, 16QAM, and 64QAM constellations. To support users in low SINR conditions, repetition of code bits is allowed (to build up SINR) in the rate  4QAM case, with repetition factors of 2, 4, 8, and 16. The modulation and coding options are summarized in Table 2.
4QAM case, with repetition factors of 2, 4, 8, and 16. The modulation and coding options are summarized in Table 2.
Required SINRs are given in Table 2 for all the data rates, corresponding to a desired packet error rate of 10% over an unfaded additive white Gaussian noise (AWGN) channel. However, because of uncertainties introduced by channel estimation errors, time and frequency variations in the channel, and also the deviation from Gaussian of the distribution of the residual interference affecting each link, the actual packet error rates resulting from these SINR thresholds could be quite far from the target of 10%.
Therefore, we implement a simple "outer loop'' to automatically adapt the SINR thresholds individually for each user, so as to lead to a packet error rate close to 10%. We initialize the SINR thresholds to the values in Table 2 (for an AWGN channel). Subsequently, whenever a packet is decoded correctly, we decrease the SINR thresholds for the corresponding user by 0.1 dB. On the other hand, when a packet decoding error occurs, we increase the thresholds for that user by 1 dB. (This is very similar to the outer power control loop commonly used in CDMA systems.) In steady state, every upward jump of 1 dB must be counteracted by 10 downward steps of 0.1 dB, implying that the packet error rate must be  , or approximately 10%.
, or approximately 10%.
At the start of each frame, the power and data rate at which each user is to transmit must be determined by the coordination cluster of APs serving it (recall that, without network MIMO, each AP constitutes a cluster by itself, while with network MIMO all APs belong to a single cluster). The choices of powers and data rates for the users are based on a target packet error rate of 10%. We use the following algorithm for this purpose.
-
(1)
Initialize all transmit powers to their maximum values. For the uplink, set
 for
for  . For the noncoordinated downlink,
. For the noncoordinated downlink, 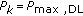 . For the coordinated downlink, set the powers
. For the coordinated downlink, set the powers 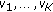 to solve the optimization problem (13).
to solve the optimization problem (13). -
(2)
Given the current power levels, compute the estimated SINR for each user. This involves finding the SINR in each channel estimation tile and averaging these SINR values over all tiles using an equivalent mutual information approach [39]. Since each tile consists of many time-frequency symbols, we can equivalently average over these symbols. The SINR
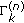 for the
for the 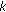 th user during symbol
th user during symbol  is given by (5), (7), (8), and (12), respectively, for noncoordinated and coordinated uplink reception and noncoordinated and coordinated downlink transmission. The average SINR for user
is given by (5), (7), (8), and (12), respectively, for noncoordinated and coordinated uplink reception and noncoordinated and coordinated downlink transmission. The average SINR for user 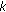 is
is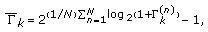 (14)
(14) -
where
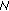 is the number of time-frequency data symbols per frame.
is the number of time-frequency data symbols per frame. -
(3)
For each user, find the highest data rate corresponding to the required SINR thresholds that can be supported at the average SINR
 . These SINR thresholds are updated each frame according to the outer loop algorithm described above.
. These SINR thresholds are updated each frame according to the outer loop algorithm described above. -
(4)
Lower each user's power to just meet the SINR requirement for the selected data rate at the targeted packet error rate (computed as if all other users are maintaining their current power levels).
-
(5)
Iterate until no user's data rate changes between successive iterations.
Between successive iterations of the above algorithm, the user powers can only decrease (see step ( )), and the user rates can only increase. Further, the set of allowable rates is finite. It follows that, after some finite number of iterations, the user rates will not change between iterations, and the algorithm will terminate. Typically, the number of iterations required is quite small.
)), and the user rates can only increase. Further, the set of allowable rates is finite. It follows that, after some finite number of iterations, the user rates will not change between iterations, and the algorithm will terminate. Typically, the number of iterations required is quite small.
5. Simulation Results
The simulation results are expressed in terms of the user goodput distribution, computed from multiple independent user drops. In each drop, users are placed in the system and their channels to all the APs are then allowed to evolve over several frames. The first 20 frames in each drop are dummy frames, whose purpose is solely to allow each user's SINR thresholds for switching between data rates to converge to values corresponding to 10% packet error rate (PER) (see Section 4.4).
Following the warmup frames, data transmission occurs over a further 50 frames. At 5 ms per frame, this corresponds to 0.25 second of real time (or about 2.5 coherence times of the channel, at 10 Hz Doppler). In each of these frames, the powers and data rates at which the users transmit are set according to the algorithm in Section 4.4. In each drop, each user's goodput (in bits/s) is computed as the ratio of the total number of information bits in the successfully decoded packets to the total time corresponding to the transmission of all data packets.
The results shown here are for a reference SNR of  40 dB. The reference SNR represents the average SNR at which a user at the midpoint between two adjacent APs would be received at either of those APs in the absence of shadow fading and interference from other users. It is a composite measure of the transmitter power available to the user, the carrier frequency and bandwidth of operation, propagation characteristics of the environment, all antenna gains, noise figures, and so forth.
40 dB. The reference SNR represents the average SNR at which a user at the midpoint between two adjacent APs would be received at either of those APs in the absence of shadow fading and interference from other users. It is a composite measure of the transmitter power available to the user, the carrier frequency and bandwidth of operation, propagation characteristics of the environment, all antenna gains, noise figures, and so forth.
Clearly, as the reference SNR is made higher, interference between users becomes more significant relative to receiver thermal noise, and therefore the mitigation of such interference through network MIMO becomes more beneficial. For system parameters of 10 MHz channel bandwidth, noise power spectral density of  174 dBm/Hz, 100 mW transmitter power, 0 dBi transmitter and receiver antenna gain, 9 dB receiver noise figure, 128 dB pathloss intercept at 1000 m, and a pathloss exponent of 3.5, the reference SNR at a reference distance of 5 m is
174 dBm/Hz, 100 mW transmitter power, 0 dBi transmitter and receiver antenna gain, 9 dB receiver noise figure, 128 dB pathloss intercept at 1000 m, and a pathloss exponent of 3.5, the reference SNR at a reference distance of 5 m is  dBm + 174 dBm
dBm + 174 dBm  10
10  dB
dB  9 dB
9 dB  128 dB + 35
128 dB + 35  dB
dB  67 dB. We restrict ourselves to a reference SNR of 40 dB since the maximum data rate is capped at the value corresponding to 64QAM and rate
67 dB. We restrict ourselves to a reference SNR of 40 dB since the maximum data rate is capped at the value corresponding to 64QAM and rate  turbo coding. (Note that the transmitter and receiver hardware will never be required to support SINR values as high as the reference SNR, because of the capping of the data rate.)
turbo coding. (Note that the transmitter and receiver hardware will never be required to support SINR values as high as the reference SNR, because of the capping of the data rate.)
Figures 3 and 4, respectively, show the CDF of uplink and downlink user goodput for three options: conventional with full frequency reuse, conventional with frequency reuse  , and network MIMO. We notice in Figure 4 that near 20% of users using the conventional transceiver under full reuse get almost zero rate. This is because the turbo codes are designed for Gaussian interference, and the non-Gaussian nature of the interference from nearby APs causes the decoders to perform poorly even at the lowest data rate. In current WiMAX systems where the maximum repetition factor is only 6 (compared to 16 in our case, according to Table 2), the fraction of users achieving zero rate would be even greater than 20%. As expected, network MIMO has a greater impact on the goodput of users in the lower tail of the distribution, since these are the ones suffering the most from interference.
, and network MIMO. We notice in Figure 4 that near 20% of users using the conventional transceiver under full reuse get almost zero rate. This is because the turbo codes are designed for Gaussian interference, and the non-Gaussian nature of the interference from nearby APs causes the decoders to perform poorly even at the lowest data rate. In current WiMAX systems where the maximum repetition factor is only 6 (compared to 16 in our case, according to Table 2), the fraction of users achieving zero rate would be even greater than 20%. As expected, network MIMO has a greater impact on the goodput of users in the lower tail of the distribution, since these are the ones suffering the most from interference.
Figure 5 shows the mean throughput and 10% outage rate for the three options. For the conventional transceiver, because frequency reuse 1/2 is better than full reuse for both mean and 10% outage rate, we consider only the former case in the remainder of the paper. At the 10th percentile, the goodput gain due to network MIMO is about a factor of 3, while at the mean it is about a factor of 2. For network MIMO, because the uplink performance is affected by channel mismatch on the uplink but the downlink performance is affected by channel mismatch on both the uplink (for computing the beamforming weights) and downlink (for data demodulation), the uplink performance is in general better.
Figure 6 shows the cumulative distribution function (CDF) of the uplink packet error rates of the users. The strong concentration around the 10% point indicates that the automatic SINR threshold adaptation algorithm described in Section 4.4 indeed works as intended. Figure 7 shows the corresponding CDF of the downlink packet error rates. The large deviation from 10% in the upper tail of the distribution without network MIMO is due to users who are in such poor channel conditions that they cannot support even the lowest data rate at the desired packet error rate.
Finally, Figure 8 shows the CDF of the margin required in the users' SINR thresholds for switching between data rates upon uplink transmission, with respect to the values required over a nonfading AWGN channel given in Table 2. Recall that these margins are required to account for imperfect channel estimation, time and frequency variations in the channel, and the deviation from a Gaussian distribution of the residual interference affecting each user after the linear MMSE or ZF beamforming. As might be expected, somewhat higher margins are required with network MIMO compared to the conventional case since most users then operate at much higher data rates, requiring more accurate channel estimates. Higher margins are also required for the downlink because it is affected by channel mismatch on both the uplink and downlink.
6. Conclusions
We have described a system simulator based on the IEEE 802.16e Mobile WiMAX standard with network MIMO processing. Results generated by the simulator have been presented for an indoor environment featuring 8 APs connected by a high-speed LAN like Gigabit Ethernet. These results confirm that, under realistic indoor operational conditions, network MIMO can provide a multiple-fold increase in spectral efficiency.
Since the physical layers of next-generation OFDM-based cellular standards are quite similar, network MIMO could potentially provide similar gains for these other standards as well. A comprehensive study of the achievable gains in typical outdoor macrocellular environments will follow. Future work must also consider the impact of fractional frequency reuse schemes on the spectral efficiency without network MIMO, as opposed to the fixed frequency reuse pattern considered here.
While this paper addresses some concerns over the viability of network MIMO in practice, several others remain, especially in the context of a larger-scale outdoor cellular deployment. Foremost among these are the bandwidth and latency requirements on the backhaul network connecting the access points to each other (or to a central processor), to facilitate the exchange of user data, channel state information, control signaling, and so forth. It would also be desirable to distribute the computation required to implement network MIMO among many nodes, so that the solution scales well with the size of the network. Finally, in a low-SNR environment, estimating the channels to/from faraway access points without excessive pilot overhead might require data-aided channel estimation algorithms. Further work is needed in all these areas to make network MIMO truly practical.
References
UTRA-UTRAN long term evolution (LTE) 3rd Generation Partnership Project (3GPP), November 2004
IEEE standard for local and metropolitan area networks—part 16: air interface for fixed broadband wireless access systems IEEE 802 LAN/MAN Standards Committee, November 2005
Wyner AD: Shannon-theoretic approach to a Gaussian cellular multipleaccess channel. IEEE Transactions on Information Theory 1994.,40(6):
Hanly S, Whiting PA: Information-theoretic capacity of multireceiver networks. Telecommunication Systems 1993, 1: 1-42. 10.1007/BF02136153
Somekh O, Shamai S: Shannon-theoretic approach to a Gaussian cellular multiple-access channel with fading. IEEE Transactions on Information Theory 2000,46(4):1401-1425. 10.1109/18.850679
Shamai S, Zaidel BM: Enhancing the cellular downlink capacity via co-processing at the transmitting end. Proceedings of the IEEE Vehicular Technology Conference (VTC '01), May 2001 3: 1745-1749.
Somekh O, Simeone O, Bar-Ness Y, Haimovich AM: Distributed multi-cell zero-forcing beamforming in cellular downlink channels. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '06), November 2006 1-6.
Jing S, Tse DNC, Soriaga JB, Hou J, Smee JE, Padovani R: Downlink macro-diversity in cellular networks. Proceedings of the IEEE International Symposium on Information Theory ((ISIT '07), June 2007, Nice, France 1-5.
Somekh O, Zaidel BM, Shamai S: Sum rate characterization of joint multiple cell-site processing. IEEE Transactions on Information Theory 2007,53(12):4473-4497.
Somekh O, Zaidel BM, Shamai S: Spectral efficiency of joint multiple cell-site processors for randomly spread DS-CDMA systems. IEEE Transactions on Information Theory 2007,53(7):2625-2637.
Shamai S, Somekh O, Simeone O, Sanderovich A, Zaidel BM, Poor HV: Cooperative multi-cell networks: impact of limited-capacity backhaul and inter-users links. Proceedings of the IEEE International Symposium on Information Theory ((ISIT '07), June 2007, Nice, France
Sanderovich A, Somekh O, Shamai S: Uplink macro diversity with limited backhaul capacity. Proceedings of the IEEE International Symposium on Information Theory ((ISIT '07), June 2007, Nice, France 11-15.
Marsch P, Fettweis G: A framework for optimizing the uplink performance of distributed antenna systems under a constrained backhaul. Proceedings of IEEE International Conference on Communications (ICC '07), June 2007 975-979.
Weber T, Maniatis I, Sklavos A, et al.: Joint transmission and detection integrated network (JOINT), a generic proposal for beyond 3G systems. Proceedings of the 9th International Conference on Telecommunications (ICT '02), 2002 479-483.
Zhang H, Dai H: Cochannel interference mitigation and cooperative processing in downlink multicell multiuser MIMO networks. EURASIP Journal on Wireless Communications and Networking 2004,2004(2):222-235.
Karakayali MK, Foschini GJ, Valenzuelat RA, Yates RD: On the maximum common rate achievable in a coordinated network. Proceedings of the IEEE International Conference on Communications (ICC '06), June 2006 9: 4333-4338.
Karakayali MK, Foschini GJ, Valenzuela RA: Network coordination for spectrally efficient communications in cellular systems. IEEE Wireless Communications June 2006,13(4):56-61. 10.1109/MWC.2006.1678166
Foschini GJ, Karakayali MK, Valenzuela RA: Coordinating multiple antenna cellular networks to achieve enormous spectral efficiency. IEE Proceedings: Communications 2006,153(4):548-555. 10.1049/ip-com:20050423
Venkatesan S: Coordinating base stations for greater uplink spectral efficiency in a cellular network. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007
Venkatesan S: Coordinating base stations for greater uplink spectral efficiency: proportionally fair user rates. Proceedings of the IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007
Zhang J, Chen R, Andrews JG, Ghosh A, Heath RW Jr.: Networked MIMO with clustered linear precoding. IEEE Transactions on Wireless Communications 2009,8(4):1910-1921.
Shi S, Schubert M, Vucic N, Boche H: MMSE optimization with per-base-station power constraints for network MIMO systems. Proceedings of the IEEE International Conference on Communications (ICC '08), May 2008 4106-4110.
Aktas E, Evans J, Hanly S: Distributed decoding in a cellular multiple-access channel. IEEE Transactions on Wireless Communications 2008,7(1):241-250.
Ng BL, Evans JS, Hanly SV, Aktas D: Distributed downlink beamforming with cooperative base stations. IEEE Transactions on Information Theory 2008,54(12):5491-5499.
Hadisusanto Y, Thiele L, Jungnickel V: Distributed base station cooperation via block-diagonalization and dual-decomposition. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '08), November-December 2008, New Orleans, La, USA 3539-3543.
Andrews JG, Choi W, Heath RW Jr.: Overcoming interference in spatial multiplexing mimo cellular networks. IEEE Wireless Communications 2007,14(6):95-104.
Cunningham DG, Lane WG: Gigabit Ethernet Networking. New Riders; 1999.
Jungnickel V, Jaeckel S, Thiele L, Krueger U, Brylka A, von Helmolt C: Capacity measurements in a multicell MIMO system. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '06), November 2006 1-6.
Jungnickel V, Jaeckel S, Thiele L, et al.: Capacity measurements in a cooperative MIMO network. IEEE transactions on vehicular technology 2009,58(5):2392-2405.
Jungnickel V, Wirth T, Schellmann M, Haustein T, Zirwas W: Synchronization of cooperative base stations. Proceedings of the IEEE International Symposium on Wireless Communication Systems (ISWCS '08), 2008 329-334.
Jandura C, Marsch P, Zoch A, Fettweis G: A testbed for cooperative multi cell algorithms. Proceedings of the Tridentcom, 2008
Zhang H, Mehta NB, Molisch AF, Zhang J, Dai H: Asynchronous interference mitigation in cooperative base station systems. IEEE Transactions on Wireless Communications 2008,7(1):155-165.
Zirwas W, Schulz E, Schubert M, Mennerich W, Jungnickel V, Thiele L: Cooperative antenna concepts for interference mitigation. Proceedings of the 13th European Wireless Conference, April 2007, Paris, France
Almers P, Bonek E, Burr A, et al.: Survey of Channel and Radio Propagation Models for WirelessMIMO Systems. EURASIP Journal on Wireless Communications and Networking 2007.,2007(1):
van Nee R, Prasad R: OFDM for Wireless Multimedia Communications. Artech House; 2000.
Yoo T, Goldsmith A: On the optimality of multi-antenna broadcast cheduling using zero-forcing beamforming. IEEE Journal on Selected Areas in Communications 2006.,24(3):
Boccardi F, Huang H: Zero-forcing precoding for the MIMO broadcast channel under per-antenna power constraints. Proceedings of the IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '06), July 2006 1-5.
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2004.
Assessment of advanced beamforming and MIMO technologies IST-2003-507581 WINNER, 2003
Acknowledgments
The authors gratefully acknowledge the assistance and support provided by Dragan Samardzija, Laurence Mailaender, Jerry Foschini, and Dmitry Chizhik, and the helpful comments from the editor and anonymous reviewers.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Venkatesan, S., Huang, H., Lozano, A. et al. A WiMAX-Based Implementation of Network MIMO for Indoor Wireless Systems. EURASIP J. Adv. Signal Process. 2009, 963547 (2009). https://doi.org/10.1155/2009/963547
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/963547


 for
for  . For the noncoordinated downlink,
. For the noncoordinated downlink, 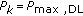 . For the coordinated downlink, set the powers
. For the coordinated downlink, set the powers 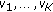 to solve the optimization problem (13).
to solve the optimization problem (13).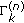 for the
for the 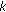 th user during symbol
th user during symbol  is given by (5), (7), (8), and (12), respectively, for noncoordinated and coordinated uplink reception and noncoordinated and coordinated downlink transmission. The average SINR for user
is given by (5), (7), (8), and (12), respectively, for noncoordinated and coordinated uplink reception and noncoordinated and coordinated downlink transmission. The average SINR for user 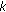 is
is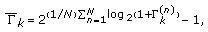
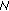 is the number of time-frequency data symbols per frame.
is the number of time-frequency data symbols per frame. . These SINR thresholds are updated each frame according to the outer loop algorithm described above.
. These SINR thresholds are updated each frame according to the outer loop algorithm described above.




