- Research Article
- Open access
- Published:
Combination of Adaptive Feedback Cancellation and Binaural Adaptive Filtering in Hearing Aids
EURASIP Journal on Advances in Signal Processing volume 2009, Article number: 968345 (2009)
Abstract
We study a system combining adaptive feedback cancellation and adaptive filtering connecting inputs from both ears for signal enhancement in hearing aids. For the first time, such a binaural system is analyzed in terms of system stability, convergence of the algorithms, and possible interaction effects. As major outcomes of this study, a new stability condition adapted to the considered binaural scenario is presented, some already existing and commonly used feedback cancellation performance measures for the unilateral case are adapted to the binaural case, and possible interaction effects between the algorithms are identified. For illustration purposes, a blind source separation algorithm has been chosen as an example for adaptive binaural spatial filtering. Experimental results for binaural hearing aids confirm the theoretical findings and the validity of the new measures.
1. Introduction
Traditionally, signal enhancement techniques for hearing aids (HAs) were mainly developed independently for each ear [1–4]. However, since the human auditory system is a binaural system combining the signals received from both ears for audio perception, providing merely bilateral systems (that operate independently for each ear) to the hearing-aid user may distort crucial binaural information needed to localize sound sources correctly and to improve speech perception in noise. Foreseeing the availability of wireless technologies for connecting the two ears, several binaural processing strategies have therefore been presented in the last decade [5–10]. In [5], a binaural adaptive noise reduction algorithm exploiting one microphone signal from each ear has been proposed. Interaural time difference cues of speech signals were preserved by processing only the high-frequency components while leaving the low frequencies unchanged. Binaural spectral subtraction is proposed in [6]. It utilizes cross-correlation analysis of the two microphone signals for a more reliable estimation of the common noise power spectrum, without requiring stationarity for the interfering noise as the single-microphone versions do. Binaural multi-channel Wiener filtering approaches preserving binaural cues were also proposed, for example, in [7–9], and signal enhancement techniques based on blind source separation (BSS) were presented in [10].
Research on feedback suppression and control system theory in general has also given rise to numerous hearing-aid specific publications in recent years. The behavior of unilateral closed-loop systems and the ability of adaptive feedback cancellation algorithms to compensate for the feedback has been extensively studied in the literature (see, e.g., [11–15]). But despite the progress in binaural signal enhancement, binaural systems have not been considered in this context. In this paper, we therefore present a theoretical analysis of a binaural system combining adaptive feedback cancellation (AFC) and binaural adaptive filtering (BAF) techniques for signal enhancement in hearing aids.
The paper is organized as follows. An efficient binaural configuration combining AFC and BAF is described in Section 2. Generic vector/matrix notations are introduced for each part of the processing chain. Interaction effects concerning the AFC are then presented in Section 3. It includes a derivation of the ideal binaural AFC solution, a convergence analysis of the AFC filters based on the binaural Wiener solution, and a stability analysis of the binaural system. Interaction effects concerning the BAF are discussed in Section 4. Here, to illustrate our argumentation, a BSS scheme has been chosen as an example for adaptive binaural filtering. Experimental conditions and results are finally presented in Sections 5 and 6 before providing concluding remarks in Section 7.
2. Signal Model
AFC and BAF techniques can be combined in two different ways. The feedback cancellation can be performed directly on the microphone inputs, or it can be applied at a later stage, to the BAF outputs. The second variant requires in general fewer filters but it has also several drawbacks. Actually, when the AFC comes after the BAF in the processing chain, the feedback cancellation task is complicated by the necessity to follow the continuously time-varying BAF filters. It may also significantly increase the necessary length of the AFC filters. Moreover, the BAF cannot benefit from the feedback cancellation effectuated by the AFC in this case. Especially at high HA amplification levels, the presence of strong feedback components in the sensor inputs may, therefore, seriously disturb the functioning of the BAF. These are structurally the same effects as those encountered when combining adaptive beamforming with acoustic echo cancellation (AEC) [16].
In this paper, we will therefore concentrate on the "AFC-first" alternative, where AFC is followed by the BAF. Figure 1 depicts the signal model adopted in this study. Each component of the signal model will be described separately in the following and generic vector/matrix notations will be introduced to carry out a general analysis of the overall system in Sections 3 and 4.
2.1. Notations
In this paper, lower-case boldface characters represent (row) vectors capturing signals or the filters of single-input-multiple-output (SIMO) systems. Accordingly, multiple-input-single-output (MISO) systems are described by transposed vectors. Matrices denoting multiple-input-multiple-output (MIMO) systems are represented by upper-case boldface characters. The transposition of a vector or a matrix will be denoted by the superscript  .
.
2.2. The Microphone Signals
We consider here multi-sensor hearing aid devices with  microphones at each ear (see Figure 1), where
microphones at each ear (see Figure 1), where  typically ranges between one and three. Because of the reverberation in the acoustical environment,
typically ranges between one and three. Because of the reverberation in the acoustical environment,  point source signals
point source signals  (
( ) are filtered by a MIMO mixing system (one
) are filtered by a MIMO mixing system (one  MIMO system for each ear in the figure) modeled by finite impulse response (FIR) filters. This can be expressed in the
MIMO system for each ear in the figure) modeled by finite impulse response (FIR) filters. This can be expressed in the  -domain as:
-domain as:

where  is the
is the  -domain representation of the received source signal mixture at the
-domain representation of the received source signal mixture at the  th sensor of the left (
th sensor of the left ( ) and right (
) and right ( ) hearing aid, respectively.
) hearing aid, respectively.  and
and  denote the transfer functions (polynomes of order up to several thousands typically) between the
denote the transfer functions (polynomes of order up to several thousands typically) between the  th source and the
th source and the  th sensor at the left and right ears, respectively. One of the point sources may be seen as the target source to be extracted, the remaining
th sensor at the left and right ears, respectively. One of the point sources may be seen as the target source to be extracted, the remaining  being considered as interfering point sources. For the sake of simplicity, the
being considered as interfering point sources. For the sake of simplicity, the  -transform dependency
-transform dependency  will be omitted in the rest of this paper, as long as the notation is not ambiguous.
will be omitted in the rest of this paper, as long as the notation is not ambiguous.
The acoustic feedback originating from the loudspeakers (LS)  and
and  at the left and right ears, respectively, is modeled by four
at the left and right ears, respectively, is modeled by four  SIMO systems of FIR filters.
SIMO systems of FIR filters.  and
and  represent the (
represent the ( -domain) transfer functions (polynomes of order up to several hundreds typically) from the loudspeakers to the
-domain) transfer functions (polynomes of order up to several hundreds typically) from the loudspeakers to the  th sensor on the left side, and
th sensor on the left side, and  and
and  represent the transfer functions from the loudspeakers to the
represent the transfer functions from the loudspeakers to the  th sensor on the right side. The feedback components captured by the
th sensor on the right side. The feedback components captured by the  th microphone of each ear can therefore be expressed in the
th microphone of each ear can therefore be expressed in the  -domain as
-domain as

Note that as long as the energy of the two LS signals are comparable, the "cross" feedback signals (traveling from one ear to the other) are negligible compared to the "direct" feedback signals (occuring on each side independently). With the feedback paths (FBP) used in this study (see the description of the evaluation data in Section 5.3), an energy difference ranging from 15 to 30 dB has been observed between the "direct" and "cross" FBP impulse responses. When the HA gains are set at similar levels in both ears, the "cross" FBPs can then be neglected. But the impact of the "cross" feedback signals becomes more significant when a large difference exists between the two HA gains. Here, therefore, we explicitly account for the two types of feedback by modelling both the "direct" paths (with transfer functions  and
and  ,
,  ) and the "cross" paths (with transfer functions
) and the "cross" paths (with transfer functions  and
and  ,
,  ) by FIR filters.
) by FIR filters.
Diffuse noise signals  and
and  ,
,  constitute the last microphone signal components on the left and right ears, respectively. The
constitute the last microphone signal components on the left and right ears, respectively. The  -domain representation of the
-domain representation of the  th sensor signal at each ear is finally given by:
th sensor signal at each ear is finally given by:

This can be reformulated in a compact matrix form jointly capturing the  microphone signals of each HA:
microphone signals of each HA:

where we have used the  -domain signal vectors
-domain signal vectors





as well as the  -domain matrices
-domain matrices










Furthermore,  and
and  capturing the noise and feedback components present in the microphone signals are defined in a similar way to
capturing the noise and feedback components present in the microphone signals are defined in a similar way to  . The sensor signal decomposition (4) can be further refined by distinguishing between target and interfering sources:
. The sensor signal decomposition (4) can be further refined by distinguishing between target and interfering sources:

 refers to the target source and
refers to the target source and  is a subset of
is a subset of  capturing the
capturing the  remaining interfering sources.
remaining interfering sources.  is a row of
is a row of  which captures the transfer functions from the target source to the sensors and
which captures the transfer functions from the target source to the sensors and  is a matrix containing the remaining
is a matrix containing the remaining  rows of
rows of  . Like the other vectors and matrices defined above, these four entities can be further decomposed into their left and right subsets, labeled with the indices
. Like the other vectors and matrices defined above, these four entities can be further decomposed into their left and right subsets, labeled with the indices  and
and  , respectively.
, respectively.
2.3. The AFC Processing
As can be seen from Figure 1, we apply here AFC to remove the feedback components present in the sensor signals, before passing them to the BAF. Feedback cancellation is achieved by trying to produce replicas of these undesired components, using a set of adaptive filters. The solution adopted here consists of two  SIMO systems of adaptive FIR filters, with transfer functions
SIMO systems of adaptive FIR filters, with transfer functions  and
and  between the left (resp. right) loudspeaker and the
between the left (resp. right) loudspeaker and the  th sensor on the left (resp. right) side. The output
th sensor on the left (resp. right) side. The output

of the  th filter on the left (resp. right) side is then subtracted from the
th filter on the left (resp. right) side is then subtracted from the  th sensor signal on the left (resp. right) side, producing a residual signal
th sensor signal on the left (resp. right) side, producing a residual signal

which is, ideally, free of any feedback components. (21) and (22) can be reformulated in matrix form as follows:

with the block-diagonal constraint

put on the AFC system. The vectors  and
and  , capturing the
, capturing the  -domain representations of the residual and AFC output signals, respectively, are defined in analogous way to
-domain representations of the residual and AFC output signals, respectively, are defined in analogous way to  in (8). As can be seen from (21) and (22), we perform here bilateral feedback cancellation (as opposed to binaural operations) since AFC is performed for each ear separately. This is reflected in (24), where we force the off-diagonal terms to be zero instead of reproducing the acoustic feedback system
in (8). As can be seen from (21) and (22), we perform here bilateral feedback cancellation (as opposed to binaural operations) since AFC is performed for each ear separately. This is reflected in (24), where we force the off-diagonal terms to be zero instead of reproducing the acoustic feedback system  with its set of four SIMO systems. The reason for this will become clear in Section 3.1. Guidelines regarding an arbitrary (i.e., unconstrained) AFC system
with its set of four SIMO systems. The reason for this will become clear in Section 3.1. Guidelines regarding an arbitrary (i.e., unconstrained) AFC system  (defined similarly to
(defined similarly to  in this case) will also be provided at some points in the paper. The superscript
in this case) will also be provided at some points in the paper. The superscript  is used to distinguish constrained systems
is used to distinguish constrained systems  defined by (24) from arbitrary (unconstrained) systems
defined by (24) from arbitrary (unconstrained) systems  (with possibly non-zero off-diagonal terms).
(with possibly non-zero off-diagonal terms).
2.4. The BAF Processing
The BAF filters perform spatial filtering to enhance the signal coming from one of the  external point sources. This is performed here binaurally, that is, by combining signals from both ears (see Figure 1). The binaural filtering operations can be described by a set of four
external point sources. This is performed here binaurally, that is, by combining signals from both ears (see Figure 1). The binaural filtering operations can be described by a set of four  MISO systems of adaptive FIR filters. This can be expressed in the
MISO systems of adaptive FIR filters. This can be expressed in the  -domain as follows:
-domain as follows:

where  and
and  ,
,  ,
,  are the transfer functions applied on the
are the transfer functions applied on the  th sensor of the left and right hearing aids, respectively. To reformulate (25) in matrix form, we define the vector
th sensor of the left and right hearing aids, respectively. To reformulate (25) in matrix form, we define the vector

which jointly captures the  -domain representations of the two BAF outputs, and the vector and matrices
-domain representations of the two BAF outputs, and the vector and matrices







related to the transfer functions of the MIMO BAF system. We can finally express (25) as:

2.5. The Forward Paths
Conventional HA processing (mainly a gain correction) is performed on the output of the AFC-BAF combination, before being played back by the loudspeakers:

where  and
and  model the HA processing in the
model the HA processing in the  -domain, at the left and right ears, respectively. In the literature, this part of the processing chain is often referred to as the forward path (in opposition to the acoustic feedback path). To facilitate the analysis, we will assume that the HA processing is linear and time-invariant (at least between two adaptation steps) in this study. (35) can be conveniently written in matrix form as:
-domain, at the left and right ears, respectively. In the literature, this part of the processing chain is often referred to as the forward path (in opposition to the acoustic feedback path). To facilitate the analysis, we will assume that the HA processing is linear and time-invariant (at least between two adaptation steps) in this study. (35) can be conveniently written in matrix form as:

with

The  operator applied to a vector builds a diagonal matrix with the vector entries placed on the main diagonal.
operator applied to a vector builds a diagonal matrix with the vector entries placed on the main diagonal.
Note that for simplicity, we assumed that the number of sensors  used on each device for digital signal processing was equal. The above notations as well as the following analysis are however readily applicable to asymmetrical configurations also, simply by resizing the above-defined vectors and matrices, or by setting the corresponding microphone signals and all the associated transfer functions to zero. In particular, the unilateral case can be seen as a special case of the binaural structure discussed in this paper, with one or more microphones used on one side, but none on the other side.
used on each device for digital signal processing was equal. The above notations as well as the following analysis are however readily applicable to asymmetrical configurations also, simply by resizing the above-defined vectors and matrices, or by setting the corresponding microphone signals and all the associated transfer functions to zero. In particular, the unilateral case can be seen as a special case of the binaural structure discussed in this paper, with one or more microphones used on one side, but none on the other side.
3. Interaction Effects on the Feedback Cancellation
The structure depicted in Figure 1 for binaural HAs mainly deviates from the well-known unilateral case by the presence of binaural spatial filtering. The binaural structure is characterized by a significantly more complex closed-loop system, possibly with multiple microphone inputs, but most importantly with two connected LS outputs, which considerably complicates the analysis of the system. However, we will see in the following how, under certain conditions, we can exploit the compact matrix notations introduced in the previous section, to describe the behavior of the closed-loop system. We will draw some interesting conclusions on the present binaural system, emphasizing its deviation from the standard unilateral case in terms of ideal cancellation solution, convergence of the AFC filters and system stability.
3.1. The Ideal Binaural AFC Solution
In the unilateral and single-channel case, the adaptation of the (single) AFC filter tries to adjust the compensation signal (the filter output) to the (single-channel) acoustic feedback signal. Under ideal conditions, this approach guarantees perfect removal of the undesired feedback components and simultaneously prevents the occurrence of howling caused by system instabilities [11] (the stability of the binaural closed-loop system will be discussed in Section 3.3). The adaptation of the filter coefficients towards the desired solution is usually achieved using a gradient-descent-like learning rule, in its simplest form using the least mean square (LMS) algorithm [17]. The functioning of the AFC in the binaural configuration shown in Figure 1 is similar.
The residual signal vector (23) can be decomposed into its source, noise and feedback components using (4):

where  denotes an arbitrary (unconstrained) AFC system matrix (Section 2.3).
denotes an arbitrary (unconstrained) AFC system matrix (Section 2.3). 

 captures the
captures the  -domain representations of the residual feedback components to be removed by the AFC. The only way to perfectly remove the feedback components from the residual signals (i.e.,
-domain representations of the residual feedback components to be removed by the AFC. The only way to perfectly remove the feedback components from the residual signals (i.e.,  ), for arbitrary output signal vectors
), for arbitrary output signal vectors  , is to have
, is to have

 denotes the ideal AFC solution in the unconstrained case. This is the binaural analogon to the ideal AFC solution in the unilateral case, where perfect cancellation is achieved by reproducing an exact replica of the acoustical FBP. In practice, this solution is however very difficult to reach adaptively because it requires the two signals
denotes the ideal AFC solution in the unconstrained case. This is the binaural analogon to the ideal AFC solution in the unilateral case, where perfect cancellation is achieved by reproducing an exact replica of the acoustical FBP. In practice, this solution is however very difficult to reach adaptively because it requires the two signals  and
and  to be uncorrelated, which is obviously not fulfilled in our binaural HA scenario since the two HAs are connected (the correlation is actually highly desirable since the HAs should form a spatial image of the acoustic scene, which implies that the two LS signals must be correlated to reflect interaural time and level differences). This problem has been extensively described in the literature on multi-channel AEC, where it is referred to as the "non-uniqueness problem". Several attempts have been reported in the literature to partly alleviate this issue (see, e.g., [18–20]). These techniques may be useful in the HA case also, but this is beyond the scope of the present work.
to be uncorrelated, which is obviously not fulfilled in our binaural HA scenario since the two HAs are connected (the correlation is actually highly desirable since the HAs should form a spatial image of the acoustic scene, which implies that the two LS signals must be correlated to reflect interaural time and level differences). This problem has been extensively described in the literature on multi-channel AEC, where it is referred to as the "non-uniqueness problem". Several attempts have been reported in the literature to partly alleviate this issue (see, e.g., [18–20]). These techniques may be useful in the HA case also, but this is beyond the scope of the present work.
In this paper, instead of trying to solve the problem mentioned above, we explicitly account for the correlation of the two LS output signals. The relation between the HA outputs can be tracked back to the relation existing between the BAF outputs  and
and  (Figure 1), which are generated from the same set of sensors and aim at reproducing a binaural impression of the same acoustical scene. The relation between
(Figure 1), which are generated from the same set of sensors and aim at reproducing a binaural impression of the same acoustical scene. The relation between  and
and  can be described by a linear operator
can be described by a linear operator  transforming
transforming  into
into  such that:
such that:

which is actually perfectly true if and only if  transforms
transforms  into
into  :
:

Therefore, the assumption (40) will only be an approximation in general, except for a specific class of BAF systems satisfying (41). The BSS algorithm discussed in Section 4 belongs to this class. Figure 2 shows the equivalent signal model resulting from (40). As can be seen from the figure,  can be equivalently considered as being part of the right forward path to further simplify the analysis. Accordingly, we then define the new vector
can be equivalently considered as being part of the right forward path to further simplify the analysis. Accordingly, we then define the new vector

jointly capturing  and the HA processing. Provided that
and the HA processing. Provided that  and
and  are linear, (41) (and hence (40) is equivalent to assuming the existence of a linear dependency between the LS outputs, which we can express as follows:
are linear, (41) (and hence (40) is equivalent to assuming the existence of a linear dependency between the LS outputs, which we can express as follows:

This assumption implies that only one filter (instead of two, one for each LS signal) suffices to cancel the feedback components in each sensor channel. It corresponds to the constraint (24) mentioned in Section 2.3, which forces the AFC system matrix  to be block-diagonal (
to be block-diagonal ( ). The required number of AFC filters reduces accordingly from
). The required number of AFC filters reduces accordingly from  to
to  .
.
Using the constraint (24) and the assumption (43) in (38), we can derive the constrained ideal AFC solution minimizing  ,
,  , considering each side separately:
, considering each side separately:

Here,  denote the ideal AFC solution for the left or right HA. It can be easily verified that inserting (44) into (23) leads to the following residual signal decomposition:
denote the ideal AFC solution for the left or right HA. It can be easily verified that inserting (44) into (23) leads to the following residual signal decomposition:

where

denotes the ideal AFC solution when  is constrained to be block-diagonal (
is constrained to be block-diagonal ( ) and under the assumption (43). The
) and under the assumption (43). The  operator is the block-wise counterpart of the
operator is the block-wise counterpart of the  operator. Applied to a list of vectors, it builds a block-diagonal matrix with the listed vectors placed on the main diagonal of the block-matrix, respectively.
operator. Applied to a list of vectors, it builds a block-diagonal matrix with the listed vectors placed on the main diagonal of the block-matrix, respectively.
To illustrate these results, we expand the ideal AFC solution (46) using (15) and (18):

For each filter, we can clearly identify two terms due to, respectively, the "direct" and "cross" FBPs (see Section 2.2). Contrary to the "direct" terms, the "cross" terms are identifiable only under the assumption (43) that the LS outputs are linearly dependent. Should this assumption not hold because of, for example, some non-linearities in the forward paths, the "cross" FBPs would not be completely identifiable. The feedback signals propagating from one ear to the other would then act as a disturbance to the AFC adaptation process. Note, however, that since the amplitude of the "cross" FBPs is negligible compared to the amplitude of the "direct" FBPs (Section 2.2), the consequences would be very limited as long as the HA gains are set to similar amplification levels, as can be seen from (47). It should also be noted that the forward path generally includes some (small) decorrelation delays  and
and  to help the AFC filters to converge to their desired solution (see Section 3.2). If those delays are set differently for each ear, causality of the "cross" terms in (47) will not always be guaranteed, in which case the ideal solution will not be achievable with the present scheme. This situation can be easily avoided by either setting the decorrelation delays
to help the AFC filters to converge to their desired solution (see Section 3.2). If those delays are set differently for each ear, causality of the "cross" terms in (47) will not always be guaranteed, in which case the ideal solution will not be achievable with the present scheme. This situation can be easily avoided by either setting the decorrelation delays  equal for each ear (which appears to be the most reasonable choice to avoid artificial interaural time differences), or by delaying the LS signals (but using the non-delayed signals as AFC filter inputs). However, since it would further increase the overall delay from the microphone inputs to the LS outputs, the latter choice appears unattractive in the HA scenario.
equal for each ear (which appears to be the most reasonable choice to avoid artificial interaural time differences), or by delaying the LS signals (but using the non-delayed signals as AFC filter inputs). However, since it would further increase the overall delay from the microphone inputs to the LS outputs, the latter choice appears unattractive in the HA scenario.
3.2. The Binaural Wiener AFC Solution
In the configuration depicted in Figure 2, similar to the standard unilateral case (see, e.g., [12]), conventional gradient-descent-based learning rules do not lead to the ideal solution discussed in Section 3.1 but to the so-called Wiener solution [17]. Actually, instead of minimizing the feedback components  in the residual signals, the AFC filters are optimized by minimizing the mean-squared error of the overall residual signals (38).
in the residual signals, the AFC filters are optimized by minimizing the mean-squared error of the overall residual signals (38).
In the following, we conduct therefore a convergence analysis of the binaural system depicted in Figure 2, by deriving the Wiener solution of the system in the frequency domain:


where the frequency dependency  was omitted in (48) and (49) for the sake of simplicity, like in the rest of this section.
was omitted in (48) and (49) for the sake of simplicity, like in the rest of this section.  is recognized as the (frequency-domain) ideal AFC solution discussed in Section 3.1, and
is recognized as the (frequency-domain) ideal AFC solution discussed in Section 3.1, and  denotes a (frequency-domain) bias term. The assumption (43) has been exploited in (48) to obtain the above final result.
denotes a (frequency-domain) bias term. The assumption (43) has been exploited in (48) to obtain the above final result.  represents the (auto-) power spectral density of
represents the (auto-) power spectral density of  ,
,  , and
, and  ,
,  , is a vector capturing cross-power spectral densities. The cross-power spectral density vectors
, is a vector capturing cross-power spectral densities. The cross-power spectral density vectors  and
and  are defined in a similar way.
are defined in a similar way.
The Wiener solution (49) shows that the optimal solution is biased due to the correlation of the different source contributions  and
and  with the reference inputs
with the reference inputs  ,
,  (i.e., the LS outputs), of the AFC filters. The bias term
(i.e., the LS outputs), of the AFC filters. The bias term  in (49) can be further decomposed like in (20), distinguishing between desired (target source) and undesired (interfering point sources and diffuse noise) sound sources:
in (49) can be further decomposed like in (20), distinguishing between desired (target source) and undesired (interfering point sources and diffuse noise) sound sources:

By nature, the spatially uncorrelated diffuse noise components  will be only weakly correlated with the LS outputs. The third bias term will have therefore only a limited impact on the convergence of the AFC filters. The diffuse noise sources will mainly act as a disturbance. Depending on the signal enhancement technique used, they might even be partly removed. But above all, the (multi-channel) BAF performs spatial filtering, which mainly affects the interfering point sources. Ideally, the interfering sources may even vanish from the LS outputs, in which case the second bias term would simply disappear. In practice, the interference sources will never be completely removed. Hence the amount of bias introduced by the interfering sources will largely depend on the interference rejection performance of the BAF. However, like in the unilateral hearing aids, the main source of estimation errors comes from the target source. Actually, since the BAF aims at producing outputs which are as close as possible to the original target source signal, the first bias term due to the (spectrally colored) target source will be much more problematic.
will be only weakly correlated with the LS outputs. The third bias term will have therefore only a limited impact on the convergence of the AFC filters. The diffuse noise sources will mainly act as a disturbance. Depending on the signal enhancement technique used, they might even be partly removed. But above all, the (multi-channel) BAF performs spatial filtering, which mainly affects the interfering point sources. Ideally, the interfering sources may even vanish from the LS outputs, in which case the second bias term would simply disappear. In practice, the interference sources will never be completely removed. Hence the amount of bias introduced by the interfering sources will largely depend on the interference rejection performance of the BAF. However, like in the unilateral hearing aids, the main source of estimation errors comes from the target source. Actually, since the BAF aims at producing outputs which are as close as possible to the original target source signal, the first bias term due to the (spectrally colored) target source will be much more problematic.
One simple way to reduce the correlation between the target source and the LS outputs is to insert some delays  and
and  in the forward paths [12]. The benefit of this method is however very limited in the HA scenario where only tiny processing delays (5 to 10 ms for moderate hearing losses) are allowed to avoid noticeable effects due to unprocessed signals leaking into the ear canal and interfering with the processed signals. Other more complicated approaches applying a prewhitening of the AFC inputs have been proposed for the unilateral case [21, 22], which could also help in the binaural case. We may also recall a well-known result from the feedback cancellation literature: the bias of the AFC solution decreases when the HA gain increases, that is, when the signal-to-feedback ratio (SFR) at the AFC inputs (the microphones) decreases. This statement also applies to the binaural case. This can be easily seen from (50) where the auto-power spectral density
in the forward paths [12]. The benefit of this method is however very limited in the HA scenario where only tiny processing delays (5 to 10 ms for moderate hearing losses) are allowed to avoid noticeable effects due to unprocessed signals leaking into the ear canal and interfering with the processed signals. Other more complicated approaches applying a prewhitening of the AFC inputs have been proposed for the unilateral case [21, 22], which could also help in the binaural case. We may also recall a well-known result from the feedback cancellation literature: the bias of the AFC solution decreases when the HA gain increases, that is, when the signal-to-feedback ratio (SFR) at the AFC inputs (the microphones) decreases. This statement also applies to the binaural case. This can be easily seen from (50) where the auto-power spectral density  decreases quadratically whereas the cross-power spectral densities increase only linearly with increasing LS signal levels.
decreases quadratically whereas the cross-power spectral densities increase only linearly with increasing LS signal levels.
Note that the above derivation of the Wiener solution has been performed under the assumption (43) that the LS outputs are linearly dependent. When this assumption does not hold, an additional term appears in the Wiener solution. We may illustrate this exemplarily for the left side, starting from (48):

The bias term is identical to the one already obtained in (50), while the desired term is now split into two parts. The first one is related to the "direct" FBPs. The second term involves the "cross" FBPs and shows that gradient-based optimization algorithms will try to exploit the correlation of the LS outputs (when existing) to remove the feedback signal components traveling from one ear to the other. In the extreme case that the two LS signals are totally decorrelated (i.e.,  ), this term disappears and the "cross" feedback signals cannot be compensated. Note, however, that it would only have a very limited impact as long as the HA gains are set to similar amplification levels, as we saw in Section 3.1.
), this term disappears and the "cross" feedback signals cannot be compensated. Note, however, that it would only have a very limited impact as long as the HA gains are set to similar amplification levels, as we saw in Section 3.1.
3.3. The Binaural Stability Condition
In this section, we formulate the stability condition of the binaural closed-loop system, starting from the general case before applying the block-diagonal constraint (24). We first need to express the responses  and
and  of the binaural system (Figure 1) on the left and right side, respectively, to an external excitation
of the binaural system (Figure 1) on the left and right side, respectively, to an external excitation  . This can be done in the
. This can be done in the  -domain as follows:
-domain as follows:


where  and
and  denote the first row of
denote the first row of  and
and  , respectively, that is, the transfer functions applied to the left LS signal.
, respectively, that is, the transfer functions applied to the left LS signal.  and
and  denote the second row of
denote the second row of  and
and  , respectively, that is, the transfer functions applied to the right LS signal.
, respectively, that is, the transfer functions applied to the right LS signal.  and
and  represent the
represent the  -domain representations of the ideal system responses, once the feedback signals have been completely removed:
-domain representations of the ideal system responses, once the feedback signals have been completely removed:

 ,
,  ,
,  , and
, and  can be interpreted as the open-loop transfer functions (OLTFs) of the system. They can be seen as the entries of the OLTF matrix
can be interpreted as the open-loop transfer functions (OLTFs) of the system. They can be seen as the entries of the OLTF matrix  defined as follows:
defined as follows:

Combining (52) and (53) finally yields the relations:

with

where the operators  and
and  denote the trace and determinant of a matrix, respectively.
denote the trace and determinant of a matrix, respectively.
Similar to the unilateral case [11], (56) indicate that the binaural closed-loop system is stable as long as the magnitude of  does not exceed one for any angular frequency
does not exceed one for any angular frequency  :
:

Here, the phase condition has been ignored, as usual in the literature on AFC [14]. Note that the function  in (57) and hence the stability of the binaural system, depend on the current state of the BAF filters.
in (57) and hence the stability of the binaural system, depend on the current state of the BAF filters.
The above derivations are valid in the general case. No particular assumption has been made and the AFC system has not been constrained to be block-diagonal. In the following, we will consider the class of algorithms satisfying the assumption (41), implying that the two BAF outputs are linearly dependent. In this case, the ideal system output vector (54) becomes

Furthermore, it can easily be verified that the following relations are satisfied in this case:



The closed-loop response (56) of the binaural system simplifies, therefore, in this case to

where  , defined in (57), reduces to
, defined in (57), reduces to

Finally, when applying additionally the block-diagonal constraint (24) on the AFC system, (64) further simplifies to

The stability condition (58) formulated on  for the general case still applies here.
for the general case still applies here.
The above results show that in the unconstrained (constrained, resp.) case, when the AFC filters reach their ideal solution  (
( , resp.), the function
, resp.), the function  in (57) (65), resp.) is equal to zero. Hence the stability condition (58) is always fulfilled, regardless of the HA amplification levels used, and the LS outputs become ideal, with
in (57) (65), resp.) is equal to zero. Hence the stability condition (58) is always fulfilled, regardless of the HA amplification levels used, and the LS outputs become ideal, with  as expected.
as expected.
4. Interaction Effects on the Binaural Adaptive Filtering
The presence of feedback in the microphone signals is usually not taken into account when developing signal enhancement techniques for hearing aids. In this section, we consider the configuration depicted in Figure 1 and focus exemplarily on BSS techniques as possible candidates to implement the BAF, thereby analyzing the impact of feedback on BSS and discussing possible interaction effects with an AFC algorithm.
4.1. Overview on Blind Source Separation
The aim of blind source separation is to recover the original source signals from an observed set of signal mixtures. The term "blind" implies that the mixing process and the original source signals are unknown. In acoustical scenarios, like in the hearing-aid application, the source signals are mixed in a convolutive manner. The (convolutive) acoustical mixing system can be modeled as a MIMO system  of FIR filters (see Section 2.2). The case where the number
of FIR filters (see Section 2.2). The case where the number  of (simultaneously active) sources is equal to the number
of (simultaneously active) sources is equal to the number  of microphones (assuming
of microphones (assuming  channels for each ear (see Section 2.2) is referred to as the determined case. The case where
channels for each ear (see Section 2.2) is referred to as the determined case. The case where  is called overdetermined, while
is called overdetermined, while  is denoted as underdetermined.
is denoted as underdetermined.
The underdetermined BSS problem can be handled based on time-frequency masking techniques, which rely on the sparseness of the sound sources (see, e.g., [23, 24]). In this paper, we assume that the number of sources does not exceed the number of microphones. Separation can then be performed using independent component analysis (ICA) methods, merely under the assumption of statistical independence of the original source signals [25]. ICA achieves separation by applying a demixing MIMO system  of FIR filters on the microphone signals, hence providing an estimate of each source at the outputs of the demixing system. This is achieved by adapting the weights of the demixing filters to force the output signals to become statistically independent. Because of the adaptation criterion exploiting the independence of the sources, a distinction between desired and undesired sources is unnecessary. Adaptation of the BSS filters is therefore possible even when all sources are simultaneously active, in contrast to more conventional techniques based on Wiener filtering [8] or adaptive beamforming [26].
of FIR filters on the microphone signals, hence providing an estimate of each source at the outputs of the demixing system. This is achieved by adapting the weights of the demixing filters to force the output signals to become statistically independent. Because of the adaptation criterion exploiting the independence of the sources, a distinction between desired and undesired sources is unnecessary. Adaptation of the BSS filters is therefore possible even when all sources are simultaneously active, in contrast to more conventional techniques based on Wiener filtering [8] or adaptive beamforming [26].
One way to solve the BSS problem is to transform the mixtures to the frequency domain using the discrete Fourier transform (DFT) and apply ICA techniques in each DFT-bin independently (see e.g., [27, 28]). This approach is referred to as the narrowband approach, in contrast with broadband approaches which process all frequency bins simultaneously. Narrowband approaches are conceptually simpler but they suffer from a permutation and scaling ambiguity in each frequency bin, which must be tackled by additional heuristic mechanisms. Note however that to solve the permutation problem, information on the sensor positions is usually required and free-field sound wave propagation is assumed (see, e.g., [29, 30]). Unfortunately, in the binaural HA application, the distance between the microphones on each side of the head will generally not be known exactly and head shadowing effects will cause a disturbance of the wavefront. In this paper, we consider a broadband ICA approach [31, 32] based on the TRINICON framework [33]. Separation is performed exploiting second-order statistics, under the assumption that the (mutually independent) source signals are non-white and non-stationary (like speech). Since this broadband approach does not rely on accurate knowledge of the sensor placement, it is robust against unknown microphone array deformations or disturbance of the wavefront. It has already been used for binaural HAs in [10, 34].
Since BSS allows the reconstruction of the original source signals up to an unknown permutation, we cannot know a-priori which output contains the target source. Here, it is assumed that the target source is located approximately in front of the HA user, which is a standard assumption in state-of-the-art HAs. Based on the approach presented in [35], the output containing the most frontal source is then selected after estimating the time-difference-of-arrival (TDOA) of each separated source. This is done by exploiting the ability of the broadband BSS algorithm [31, 32] to perform blind system identification of the acoustical mixing system. Figure 3 illustrates the resulting AFC-BSS combination. Note that the BSS algorithm can be embedded into the general binaural configuration depicted in Figure 1, with the BAF filters  and
and  set identically to the BSS filters producing the selected (monaural) BSS output:
set identically to the BSS filters producing the selected (monaural) BSS output:


The BSS algorithm satisfies, therefore, the assumption (41) and the AFC-BSS combination can be equivalently described by Figure 2, with  . In the following,
. In the following,  refers to the selected BSS output presented (after amplification in the forward paths) to the HA user at both ears, and
refers to the selected BSS output presented (after amplification in the forward paths) to the HA user at both ears, and  denotes the transfer functions of the selected BSS filters (common to both LS outputs). Note finally that post-processing filters may be used to recover spatial cues [10]. They can be modelled as being part of the forward paths
denotes the transfer functions of the selected BSS filters (common to both LS outputs). Note finally that post-processing filters may be used to recover spatial cues [10]. They can be modelled as being part of the forward paths  and
and  .
.
4.2. Discussion
In the HA scenario, since the LS output signals feed back into the microphones, the closed-loop system formed by the HAs participates in the source mixing process, together with the acoustical mixing system. Therefore, the BSS inputs result from a mixture of the external sources and the feedback signals coming from the loudspeakers. But because of the closed-loop system bringing the HA inputs to the two LS outputs, the feedback signals are correlated with the original external source signals. To understand the impact of feedback on the separation performance of a BSS algorithm, we describe below the overall mixing process.
The closed-loop transfer function from the external sources (the point sources and the diffuse noise sources) to the BSS inputs (i.e, the residual signals after AFC) can be expressed in the  -domain by inserting (59) and (63) into (45):
-domain by inserting (59) and (63) into (45):

where  and
and  refer to the AFC system and its ideal solution (46), respectively, under the block-diagonal constraint (24).
refer to the AFC system and its ideal solution (46), respectively, under the block-diagonal constraint (24).  characterizes the stability of the binaural closed-loop system and is defined by (65). From (68), we can identify two independent components
characterizes the stability of the binaural closed-loop system and is defined by (65). From (68), we can identify two independent components  and
and  present in the BSS inputs and originating from the external point sources and from the diffuse noise, respectively. As mentioned in Section 4.1, the BSS algorithm allows to separate point sources, additional diffuse noise having only a limited impact on the separation performance [32]. We therefore concentrate on the first term in (68):
present in the BSS inputs and originating from the external point sources and from the diffuse noise, respectively. As mentioned in Section 4.1, the BSS algorithm allows to separate point sources, additional diffuse noise having only a limited impact on the separation performance [32]. We therefore concentrate on the first term in (68):

which produces an additional mixing system  introduced by the acoustical feedback (and the required AFC filters). Ideally, the BSS filters should converge to a solution which minimizes the contribution
introduced by the acoustical feedback (and the required AFC filters). Ideally, the BSS filters should converge to a solution which minimizes the contribution  of the interfering point sources
of the interfering point sources  at the BSS output
at the BSS output  , that is,
, that is,

 refers to the acoustical mixing of the interfering sources
refers to the acoustical mixing of the interfering sources  , as defined in Section 2.2.
, as defined in Section 2.2.  can be defined in a similar way and describes the mixing of the interfering sources introduced by the feedback loop.
can be defined in a similar way and describes the mixing of the interfering sources introduced by the feedback loop.
In the absence of feedback (and of AFC filters), the second term in (70) disappears and BSS can extract the target source by unraveling the acoustical mixing system  , which is the desired solution. Note that this solution also allows to estimate the position of each source, which is necessary to select the output of interest, as discussed in Section 4.1. However, when strong feedback signal components are present at the BSS inputs, the BSS solution becomes biased since the algorithm will try to unravel the feedback loop
, which is the desired solution. Note that this solution also allows to estimate the position of each source, which is necessary to select the output of interest, as discussed in Section 4.1. However, when strong feedback signal components are present at the BSS inputs, the BSS solution becomes biased since the algorithm will try to unravel the feedback loop  instead of targetting the acoustical mixing system
instead of targetting the acoustical mixing system  only. The importance of the bias depends on the magnitude response of the filters captured by
only. The importance of the bias depends on the magnitude response of the filters captured by  in (70), relative to the magnitude response of the filters captured by
in (70), relative to the magnitude response of the filters captured by  . Contrary to the AFC bias encountered in Section 3.2, the BSS bias therefore decreases with increasing SFR.
. Contrary to the AFC bias encountered in Section 3.2, the BSS bias therefore decreases with increasing SFR.
The above discussion concerning BSS algorithms can be generalized to any signal enhancement techniques involving adaptive filters. The presence of feedback at the algorithm's inputs will always cause some adaptation problems. Fortunately, placing an AFC in front of the BAF like in Figure 1 can help increasing the SFR at the BAF inputs. In particular, when the AFC filters reach their ideal solution (i.e.,  ), then
), then  becomes zero and the bias term due to the feedback loop in (70) disappears, regardless of the amount of sound amplification applied in the forward paths.
becomes zero and the bias term due to the feedback loop in (70) disappears, regardless of the amount of sound amplification applied in the forward paths.
5. Evaluation Setup
To validate the theoretical analysis conducted in Sections 3 and 4, the binaural configuration depicted in Figure 3 was experimentally evaluated for the combination of a feedback canceler and the blind source separation algorithm introduced in Section 4.1.
5.1. Algorithms
The BSS processing was performed using a two-channel version of the algorithm introduced in Section 4.1, picking up the front microphone at each ear (i.e.,  ). Four adaptive BSS filters needed to be computed at each adaptation step. The output containing the target source (the most frontal one) was selected based on BSS-internal source localization (see Section 4.1, and [35]). To obtain meaningful results which are, as far as possible, independent of the AFC implementation used, the AFC filter update was performed based on the frequency-domain adaptive filtering (FDAF) algorithm [36]. The FDAF algorithm allows for an individual step-size control for each DFT bin and a bin-wise optimum control mechanism of the step-size parameter, derived from [13, 37]. In practice, this optimum step-size control mechanism is inappropriate since it requires the knowledge of signals which are not available under real conditions, but it allows us to minimize the impact of a particular AFC implementation by providing useful information on the achievable AFC performance. Since we used two microphones, the (block-diagonal constrained) AFC consisted of two adaptive filters (see Figure 3).
). Four adaptive BSS filters needed to be computed at each adaptation step. The output containing the target source (the most frontal one) was selected based on BSS-internal source localization (see Section 4.1, and [35]). To obtain meaningful results which are, as far as possible, independent of the AFC implementation used, the AFC filter update was performed based on the frequency-domain adaptive filtering (FDAF) algorithm [36]. The FDAF algorithm allows for an individual step-size control for each DFT bin and a bin-wise optimum control mechanism of the step-size parameter, derived from [13, 37]. In practice, this optimum step-size control mechanism is inappropriate since it requires the knowledge of signals which are not available under real conditions, but it allows us to minimize the impact of a particular AFC implementation by providing useful information on the achievable AFC performance. Since we used two microphones, the (block-diagonal constrained) AFC consisted of two adaptive filters (see Figure 3).
Finally, to avoid other sources of interaction effects and concentrate on the AFC-BSS combination, we considered a simple linear time-invariant frequency-independent hearing-aid processing in the forward paths (i.e.,  and
and  ). Furthermore, in all the results presented in Section 4, the same HA gains
). Furthermore, in all the results presented in Section 4, the same HA gains  and decorrelation delays (see Section 3.2)
and decorrelation delays (see Section 3.2)  were applied at both ears. The selected BSS output was therefore amplified by a factor
were applied at both ears. The selected BSS output was therefore amplified by a factor  , delayed by
, delayed by  and played back at the two LS outputs.
and played back at the two LS outputs.
5.2. Performance Measures
We saw in the previous sections that our binaural configuration significantly differs from what can usually be found in the literature on unilateral HAs. To be able to objectively evaluate the algorithms' performance in this context, especially concerning the AFC, we need to adapt some of the already existing and commonly used performance measures to the new binaural configuration. This issue is discussed in the following, based on the outcomes of the theoretical analysis presented in Sections 3 and 4.
5.2.1. Feedback Cancellation Performance Measures
In the conventional unilateral case, the feedback cancellation performance is usually measured in terms of misalignment between the (single) FBP estimate and the true (single) FBP (which is the ideal solution in the unilateral case), as well as in terms of Added Stable Gain (ASG) reflecting the benefit of AFC for the user [14].
In the binaural configuration considered in this study, the misalignment should measure the mismatch between each AFC filter and its corresponding ideal solution. This can be computed in the frequency domain as follows:

The ideal binaural AFC solution has been defined in (39) for the general case, and in (44) under the block-diagonal constraint (24) and assumption (43). In the results presented in Section 4, the misalignment has been averaged over all AFC filters (two filters in our case).
In general, it is not possible to calculate an ASG in the binaural case since the function  characterizing the stability of the system depends on both gains
characterizing the stability of the system depends on both gains  and
and  (Section 3.3). It is however possible to calculate an added stability margin (ASM) measuring the additional gain margin (the distance of
(Section 3.3). It is however possible to calculate an added stability margin (ASM) measuring the additional gain margin (the distance of  to 0dB, see Figure 4) obtained by the AFC
to 0dB, see Figure 4) obtained by the AFC

where  has been defined in (57) and
has been defined in (57) and  is the initial magnitude of
is the initial magnitude of  , without AFC. Since the assumption (41) is valid in our case (with
, without AFC. Since the assumption (41) is valid in our case (with  ) and since we force our AFC system to be block-diagonal, we can alternatively use the simplified expression of
) and since we force our AFC system to be block-diagonal, we can alternatively use the simplified expression of  given by (65). Note that the initial stability margin
given by (65). Note that the initial stability margin  as well as the margin with AFC
as well as the margin with AFC  , and hence the ASM, depend not only on the acoustical (binaural) FBPs, but also on the current state of the BAF filters. Also, when
, and hence the ASM, depend not only on the acoustical (binaural) FBPs, but also on the current state of the BAF filters. Also, when  ,
,  becomes directly proportional to
becomes directly proportional to  and the ASM can be interpreted as an ASG.
and the ASM can be interpreted as an ASG.
Additionally, the SFR measured at the BSS and AFC inputs should be taken into account when assessing the AFC-BSS combination since it directly influences the performance of the algorithms. The SFR is defined in the following as the signal power ratio between the components coming from the external sources (without distinction between desired and interfering sources), and the components coming from loudspeakers (i.e., the feedback signals).
5.2.2. Signal Enhancement Performance Measures
The separation performance of the BSS algorithm is evaluated in terms of signal-to-interference ratio (SIR), that is, the signal power ratio between the components coming from the target source and the components coming from the interfering source(s). Although the feedback components  and the AFC filter outputs
and the AFC filter outputs  (i.e., the compensation signals) contain some signal coming from the external sources
(i.e., the compensation signals) contain some signal coming from the external sources  (which causes a bias of the BSS solution, as discussed in Section 4), we will ignore them in the SIR calculation since these components are undesired. An SIR gain can then be obtained as the difference between the SIR at the BSS inputs and the SIR at the BSS outputs. It reflects the ability of BSS to extract the desired components from the signal mixture
(which causes a bias of the BSS solution, as discussed in Section 4), we will ignore them in the SIR calculation since these components are undesired. An SIR gain can then be obtained as the difference between the SIR at the BSS inputs and the SIR at the BSS outputs. It reflects the ability of BSS to extract the desired components from the signal mixture  , regardless of the amount of feedback (or background noise) present. Since only one BSS output is presented to the HA user (Section 4.1), we average the input SIR over all BSS input channels (here two), but we consider only the selected BSS output for the output SIR calculations.
, regardless of the amount of feedback (or background noise) present. Since only one BSS output is presented to the HA user (Section 4.1), we average the input SIR over all BSS input channels (here two), but we consider only the selected BSS output for the output SIR calculations.
5.3. Experimental Conditions
Since a two-channel ICA-based BSS algorithm can only separate two point sources (Section 4.1), no diffuse noise has been added to the sensor signal mixture (i.e.,  ) and only two point sources were considered (one target source and one interfering source).
) and only two point sources were considered (one target source and one interfering source).
Head-related impulse responses (HRIR) were measured using a pair of Siemens Life (BTE) hearing aid cases with two microphones and a single receiver (loudspeaker) inside each device (no processor). The cases were mounted on a real person and connected, via a pre-amplifier box, to a (laptop) PC equipped with a multi-channel RME Multiface sound card. Measurements were made in the following environments:
-
(i)
a low-reverberation chamber (
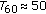 ?ms),
?ms), -
(ii)
a living-room-like environment (
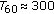 ?ms).
?ms).
The source signal components  were then generated by convolving speech signals with the recorded HRIRs, with the target and interfering sources placed at azimuths
were then generated by convolving speech signals with the recorded HRIRs, with the target and interfering sources placed at azimuths  (in front of the HA user) and
(in front of the HA user) and  (facing the right ear), respectively. The target and interfering sources were approximately of equal (long-time) signal power.
(facing the right ear), respectively. The target and interfering sources were approximately of equal (long-time) signal power.
To generate the feedback components  , binaural FBPs ("direct" and "cross" FBPs, see Section 2.2) measured from Siemens BTE hearing aids were used. These recordings have been made for different vent sizes: 2 mm, 3 mm and open and in the following scenario:
, binaural FBPs ("direct" and "cross" FBPs, see Section 2.2) measured from Siemens BTE hearing aids were used. These recordings have been made for different vent sizes: 2 mm, 3 mm and open and in the following scenario:
-
(i)
left HA mounted on a manikin without obstruction,
-
(ii)
right HA mounted on a manikin with a telephone as obstruction.
The digital signal processing was performed at a sampling frequency of  kHz, picking up the front microphone at each ear (i.e.,
kHz, picking up the front microphone at each ear (i.e.,  ).
).
6. Experimental Results
In the following, experimental results involving the combination of AFC and BSS are shown and discussed. BSS filters of 1024 coefficients each were applied, the AFC filter length was set to 256 and decorrelation delays of 5 ms were included in the forward paths.
6.1. Impact of Feedback on BSS
The discussion of Section 4 indicates that a deterioration of the BSS performance is expected at low input SFR, due to a bias introduced by the feedback loop. To determine to which extent the amount of feedback deteriorates the achievable source separation, the performance of the (adaptive) BSS algorithm was experimentally evaluated for different amounts of feedback by varying the amplification level  . Preliminary tests in the absence of AFC showed that the feedback had almost no impact on the BSS performance as long as the system was stable (i.e., as long as
. Preliminary tests in the absence of AFC showed that the feedback had almost no impact on the BSS performance as long as the system was stable (i.e., as long as  ) because the SFR at the BSS inputs was kept high (greater than 20 dB). This basically validates the traditional way signal enhancement techniques for hearing aids have been developed, ignoring the presence of feedback.
) because the SFR at the BSS inputs was kept high (greater than 20 dB). This basically validates the traditional way signal enhancement techniques for hearing aids have been developed, ignoring the presence of feedback.
Signal enhancement algorithms, however, can be subject to higher input SFR levels when an AFC is used to stabilize the system. To be able to further increase the gains and the amount of feedback signal in the microphone inputs while preventing system instability, the feedback components present at the BSS output  were artificially suppressed. This is equivalent to performing AFC on the BSS output, under ideal conditions. It guarantees the stability of the system (with
were artificially suppressed. This is equivalent to performing AFC on the BSS output, under ideal conditions. It guarantees the stability of the system (with  ), regardless of the HA amplification level, but does not reduce the SFR at the BSS inputs. The results after convergence of the BSS algorithm are presented in Figures 5 and 6 for different rooms and vent sizes. The reference lines show the gain in SIR achieved by BSS in the absence of feedback (and hence in the absence of AFC). The critical gain depicted by vertical dashed lines in the figures, corresponds to the maximum stable gain without AFC, that is, the gain for which the initial stability margin
), regardless of the HA amplification level, but does not reduce the SFR at the BSS inputs. The results after convergence of the BSS algorithm are presented in Figures 5 and 6 for different rooms and vent sizes. The reference lines show the gain in SIR achieved by BSS in the absence of feedback (and hence in the absence of AFC). The critical gain depicted by vertical dashed lines in the figures, corresponds to the maximum stable gain without AFC, that is, the gain for which the initial stability margin  becomes zero.
becomes zero.
At low gains, the feedback has very little impact on the SIR gain because the input SFR is sufficiently high in all tested scenarios. We see also that the interference rejection causes a decrease in SFR (from the BSS inputs to the output) since parts of the external source components are attenuated. This should be beneficial to an AFC algorithm since it reduces the bias of the AFC Wiener solution due to the interfering source, as discussed in Section 3.2. However, at high gains, where the input SFR is low (less than 10 dB), the large amount of feedback causes a significant deterioration of the interference rejection performance. Moreover, it should be noted that at low gains, the input SFR decreases proportionally to the gain, as expected. We see, however, from the figures that the input SFR suddenly drops at higher gains, when the amount of feedback becomes significant (see, e.g., the transition from  20 dB to
20 dB to  25 dB, in Figure 6, for an open vent). Since BSS has no influence on the signal power of the external sources (the "S" component in the SFR), it means that BSS amplifies the LS signals (and hence the feedback signals at the microphones, that is, the "F" component in the SFR). This undesired effect is due to the bias introduced by the feedback loop (Section 4.2) and can be interpreted as follows: two mechanisms enter into play. The first one unravels the acoustical mixing system. It produces LS signals which are dominated by the target source (see the positive SIR gains in the figures), as desired. The second mechanism consists in amplifying the sensor signals. As long as the feedback level is small, this second mechanism is almost invisible since it would amplify signals coming from both sources. But at higher gains, where the amount of feedback in the BSS inputs become more significant, this second mechanism becomes more important since it acts mainly in favor of the target source. This second mechanism illustrates the impact of the feedback loop on the BSS algorithm at high feedback levels. It shows the necessity to have the AFC placed before BSS, so that BSS can benefit from a higher input SFR.
25 dB, in Figure 6, for an open vent). Since BSS has no influence on the signal power of the external sources (the "S" component in the SFR), it means that BSS amplifies the LS signals (and hence the feedback signals at the microphones, that is, the "F" component in the SFR). This undesired effect is due to the bias introduced by the feedback loop (Section 4.2) and can be interpreted as follows: two mechanisms enter into play. The first one unravels the acoustical mixing system. It produces LS signals which are dominated by the target source (see the positive SIR gains in the figures), as desired. The second mechanism consists in amplifying the sensor signals. As long as the feedback level is small, this second mechanism is almost invisible since it would amplify signals coming from both sources. But at higher gains, where the amount of feedback in the BSS inputs become more significant, this second mechanism becomes more important since it acts mainly in favor of the target source. This second mechanism illustrates the impact of the feedback loop on the BSS algorithm at high feedback levels. It shows the necessity to have the AFC placed before BSS, so that BSS can benefit from a higher input SFR.
6.2. Overall Behavior of the AFC-BSS Combination
The full AFC-BSS combination has been evaluated for a vent size of 2 mm, in the low-reverberation chamber as well as in the living-room-like environment (Section 5.3). Figure 7 depicts the BSS and AFC performance obtained after convergence. Like in Figures 5 and 6, the reference lines show the gain in SIR achieved by BSS in the absence of feedback (and hence in the absence of AFC).
The results confirm the observations made in the previous section. With the AFC applied directly on the sensor signals, the BSS algorithm could indeed benefit from the ability of the AFC to keep the SFR at the BSS inputs at high levels for every considered HA gains. Therefore, BSS always provided SIR gains which were very close to the reference SIR gain obtained without feedback, even at high gains. This contrasts with the results obtained in Figures 5 and 6, where an ideal AFC was applied at the BSS output instead of being applied first.
Note that the SFR at the AFC outputs correspond here to the SFR at the BSS inputs. The gain in SFR ( , i.e., the feedback attenuation) achieved by the AFC algorithm can be therefore directly visualized from Figure 7. As expected from the discussion presented in Section 3.1, the two AFC filters used were sufficient to efficiently compensate both the "direct" and "cross" feedback signals, and hence avoid instability of the binaural closed-loop system. Like in the unilateral case and as expected from the convergence analysis conducted in Section 3.2, the best AFC results were obtained at low input SFR levels, that is, at high gains. The AFC performance was also better in the low-reverberation chamber than in the living-room-like environment, as can be seen from the higher SFR levels at the BSS inputs, the higher ASM values and the lower misalignments. This result seems surprising at the first sight, since the FBPs were identical in both environments. It can be however easily justified by the analytical results presented in Section 3.2. We saw actually that the correlation between the external source signals and the LS signals introduce a bias of the AFC Wiener solution. The bias due to the target source is barely influenced by the BSS results since BSS left the target signal (almost) unchanged in both environments. But the BSS performance influences directly the amount of residual interfering signal present at the LS outputs, and hence the bias of the AFC Wiener solution due to the interfering source. In general, since reverberation increases the length of the acoustical mixing filters (and hence the necessary BSS filter length, typically), the more reverberant the environment, the lower the achieved separation results (for a given BSS filter length). This is confirmed here by the SIR results shown in the figures. The difference in AFC performance comes therefore from the higher amount of residual interfering signal present at the LS outputs in the living-room-like environment, which increases the bias of the AFC Wiener solution.
, i.e., the feedback attenuation) achieved by the AFC algorithm can be therefore directly visualized from Figure 7. As expected from the discussion presented in Section 3.1, the two AFC filters used were sufficient to efficiently compensate both the "direct" and "cross" feedback signals, and hence avoid instability of the binaural closed-loop system. Like in the unilateral case and as expected from the convergence analysis conducted in Section 3.2, the best AFC results were obtained at low input SFR levels, that is, at high gains. The AFC performance was also better in the low-reverberation chamber than in the living-room-like environment, as can be seen from the higher SFR levels at the BSS inputs, the higher ASM values and the lower misalignments. This result seems surprising at the first sight, since the FBPs were identical in both environments. It can be however easily justified by the analytical results presented in Section 3.2. We saw actually that the correlation between the external source signals and the LS signals introduce a bias of the AFC Wiener solution. The bias due to the target source is barely influenced by the BSS results since BSS left the target signal (almost) unchanged in both environments. But the BSS performance influences directly the amount of residual interfering signal present at the LS outputs, and hence the bias of the AFC Wiener solution due to the interfering source. In general, since reverberation increases the length of the acoustical mixing filters (and hence the necessary BSS filter length, typically), the more reverberant the environment, the lower the achieved separation results (for a given BSS filter length). This is confirmed here by the SIR results shown in the figures. The difference in AFC performance comes therefore from the higher amount of residual interfering signal present at the LS outputs in the living-room-like environment, which increases the bias of the AFC Wiener solution.
The AFC does not suffer from any particular negative interactions with the BSS algorithm since it comes first in the processing chain, but rather benefits from BSS, especially in the low-reverberation chamber, as we just saw. Note that the situation is very different when the AFC is applied after BSS. In this case, the AFC filters need to quickly follow the continuously time-varying BSS filters, which prevents proper convergence of the AFC filters, even with time-invariant FBPs.
7. Conclusions
An analysis of a system combining adaptive feedback cancellation and adaptive binaural filtering for signal enhancement in hearing aids was presented. To illustrate our study, a blind source separation algorithm was chosen as an example for adaptive binaural filtering. A number of interaction effects could be identified. Moreover, to correctly understand the behavior of the AFC, the system was described and analyzed in detail. A new stability condition adapted to the binaural configuration could be derived, and adequate performance measures were proposed which account for the specificities of the binaural system. Experimental evaluations confirmed and illustrated the theoretical findings.
The ideal AFC solution in the new binaural configuration could be identified but a steady-state analysis showed that the AFC suffers from a bias in its optimum (Wiener) solution. This bias, similar to the unilateral case, is due to the correlation between feedback and external source signals. It was also demonstrated theoretically as well as experimentally that a signal enhancement algorithm could help reducing this bias. The correlation between feedback and external source signals also causes a bias of the BAF solution. But contrary to the bias encountered by the AFC, the BAF bias increases with increasing HA amplification levels. Fortunately, this bias can be reduced by applying AFC on the sensor signals directly, instead of applying it on the BAF outputs.
The analysis also showed that two SIMO AFC systems of adaptive filters can effectively compensate for the four SIMO FBP systems when the outputs are sufficiently correlated (see Section 3.1). Should this condition not be fulfilled because of, for example, some non-linearities in the forward paths, the "cross" feedback signals travelling from one ear to the other would not be completely identifiable. But we saw that since the amplitude of the "cross" FBPs is usually negligible compared to the amplitude of the "direct" FBPs, the consequences would be very limited as long as the HA gains are set to similar amplification levels.
References
Doclo S, Moonen M: GSVD-based optimal filtering for single and multimicrophone speech enhancement. IEEE Transactions on Signal Processing 2002,50(9):2230-2244. 10.1109/TSP.2002.801937
Spriet A, Moonen M, Wouters J: Spatially pre-processed speech distortion weighted multi-channel Wiener filtering for noise reduction. Signal Processing 2004,84(12):2367-2387. 10.1016/j.sigpro.2004.07.028
Doclo S, Spriet A, Moonen M, Wouters J: Design of a robust multi-microphone noise reduction algorithm for hearing instruments. Proceedings of the International Symposium on Mathematical Theory of Networks and Systems (MTNS '04), July 2004, Leuven, Belgium 1-9.
Vanden Berghe J, Wouters J: An adaptive noise canceller for hearing aids using two nearby microphones. Journal of the Acoustical Society of America 1998,103(6):3621-3626. 10.1121/1.423066
Welker DP, Greenberg JE, Desloge JG, Zurek PM: Microphone-array hearing aids with binaural output—part II: a two-microphone adaptive system. IEEE Transactions on Speech and Audio Processing 1997,5(6):543-551. 10.1109/89.641299
Doerbecker M, Ernst S: Combination of two-channel spectral subtraction and adaptive Wiener post-filtering for noise reduction and dereverberation. Proceedings of the 8th European Signal Processing Conference (EUSIPCO '96), September 1996, Trieste, Italy 995-998.
Klasen TJ, van den Bogaert T, Moonen M, Wouters J: Binaural noise reduction algorithms for hearing aids that preserve interaural time delay cues. IEEE Transactions on Signal Processing 2007,55(4):1579-1585.
Doclo S, Dong R, Klasen TJ, Wouters J, Haykin S, Moonen M: Extension of the multi-channel Wiener filter with ITD cues for noise reduction in binaural hearing aids. Proceedings of IEEE Workshop on Applications of Signal Processing to Audio and Acoustics (WASPAA '05), October 2005, New Paltz, NY, USA 70-73.
Klasen TJ, Doclo S, van den Bogaert T, Moonen M, Wouters J: Binaural multi-channel Wiener filtering for hearing aids: preserving interaural time and level differences. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006, Toulouse, France 5: 145-148.
Aichner R, Buchner H, Zourub M, Kellermann W: Multi-channel source separation preserving spatial information. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '07), May 2007, Honolulu, Hawaii, USA 1: 5-8.
Egolf DP: Review of the acoustic feedback literature for a control systems point of view. In The Vanderbilt Hearing-Aid Report. York Press, London, UK; 1982:94-103.
Siqueira MG, Alwan A: Steady-state analysis of continuous adaptation in acoustic feedback reduction systems for hearing-aids. IEEE Transactions on Speech and Audio Processing 2000,8(4):443-453. 10.1109/89.848225
Puder H, Beimel B: Controlling the adaptation of feedback cancellation filters—problem analysis and solution approaches. Proceedings of the 12th European Conference on Signal Processing (EUSIPCO '04), September 2004, Vienna, Austria 25-28.
Spriet A: Adaptive filtering techniques for noise reduction and acoustic feedback cancellation in hearing aids, Ph.D. thesis. Katholieke Universiteit Leuven, Leuven, Belgium; 2004.
Spriet A, Rombouts G, Moonen M, Wouters J: Combined feedback and noise suppression in hearing aids. IEEE Transactions on Audio, Speech, and Language Processing 2007,15(6):1777-1790.
Kellermann W: Strategies for combining acoustic echo cancellation and adaptive beamforming microphone arrays. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '97), April 1997, Munich, Germany 1: 219-222.
Haykin S: Adaptive Filter Theory, Prentice Hall Information and System Sciences Series. 4th edition. Prentice Hall, Upper Saddle River, NJ, USA; 2002.
Sondhi MM, Morgan DR, Hall JL: Stereophonic acoustic echo cancellation—an overview of the fundamental problem. IEEE Signal Processing Letters 1995,2(8):148-151. 10.1109/97.404129
Benesty J, Morgan DR, Sondhi MM: A better understanding and an improved solution to the specific problems of stereophonic acoustic echo cancellation. IEEE Transactions on Speech and Audio Processing 1998,6(2):156-165. 10.1109/89.661474
Morgan DR, Hall JL, Benesty J: Investigation of several types of nonlinearities for use in stereo acoustic echo cancellation. IEEE Transactions on Speech and Audio Processing 2001,9(6):686-696. 10.1109/89.943346
Spriet A, Proudler I, Moonen M, Wouters J: An instrumental variable method for adaptive feedback cancellation in hearing aids. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '05), March 2005, Philadelphia, Pa, USA 3: 129-132.
van Waterschoot T, Moonen M: Adaptive feedback cancellation for audio signals using a warped all-pole near-end signal model. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '08), April 2008, Las Vegas, Nev, USA 269-272.
Araki S, Sawada H, Mukai R, Makino S: A novel blind source separation method with observation vector clustering. Proceedings of the International Workshop on Acoustic Echo and Noise Control (IWAENC '05), September 2005, Eindhoven, The Netherlands 117-120.
Cermak J, Araki S, Sawada H, Makino S: Blind source separation based on a beamformer array and time frequency binary masking. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '07), May 2007, Honolulu, Hawaii, USA 1: 145-148.
Hyvaerinen A, Karhunen J, Oja E: Independent Component Analysis. John Wiley & Sons, New York, NY, USA; 2001.
Herbordt W: Sound Capture for Human /Machine Interfaces. Springer, Berlin, Germany; 2005.
Parra L, Spence C: Convolutive blind separation of non-stationary sources. IEEE Transactions on Speech and Audio Processing 2000,8(3):320-327. 10.1109/89.841214
Sawada H, Mukai R, Araki S, Makino S: Polar coordinate based nonlinear function for frequency-domain blind source separation. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '02), May 2002, Orlando, Fla, USA 1: 1001-1004.
Kurita S, Saruwatari H, Kajita S, Takeda K, Itakura F: Evaluation of blind signal separation method using directivity pattern under reverberant conditions. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '00), June 2000, Istanbul, Turkey 5: 3140-3143.
Sawada H, Mukai R, Araki S, Makino S: A robust and precise method for solving the permutation problem of frequency-domain blind source separation. IEEE Transactions on Speech and Audio Processing 2004,12(5):530-538. 10.1109/TSA.2004.832994
Buchner H, Aichner R, Kellermann W: A generalization of blind source separation algorithms for convolutive mixtures based on second-order statistics. IEEE Transactions on Speech and Audio Processing 2005,13(1):120-134.
Aichner R, Buchner H, Yan F, Kellermann W: A real-time blind source separation scheme and its application to reverberant and noisy acoustic environments. Signal Processing 2006,86(6):1260-1277. 10.1016/j.sigpro.2005.06.022
Buchner H, Aichner R, Kellermann W: TRINICON: a versatile framework for multichannel blind signal processing. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '04), May 2004, Montreal, Canada 3: 889-892.
Eneman K, Luts H, Wouters J, et al.: Evaluation of signal enhancement algorithms for hearing instruments. Proceedings of the 16th European Signal Processing Conference (EUSIPCO '08), August 2008, Lausanne, Switzerland 1-5.
Buchner H, Aichner R, Stenglein J, Teutsch H, Kellennann W: Simultaneous localization of multiple sound sources using blind adaptive MIMO filtering. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '05), March 2005, Philadelphia, Pa, USA 3: 97-100.
Shynk JJ: Frequency-domain and multirate adaptive filtering. IEEE Signal Processing Magazine 1992,9(1):14-37. 10.1109/79.109205
Mader A, Puder H, Schmidt GU: Step-size control for acoustic echo cancellation filters—an overview. Signal Processing 2000,80(9):1697-1719. 10.1016/S0165-1684(00)00082-7
Acknowledgments
This work has been supported by a grant from the European Union FP6 Project 004171 HEARCOM (http://hearcom.eu/main_de.html). We would also like to thank Siemens Audiologische Technik, Erlangen, for providing some of the hearing-aid recordings for evaluation.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lombard, A., Reindl, K. & Kellermann, W. Combination of Adaptive Feedback Cancellation and Binaural Adaptive Filtering in Hearing Aids. EURASIP J. Adv. Signal Process. 2009, 968345 (2009). https://doi.org/10.1155/2009/968345
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/968345




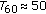 ?ms),
?ms),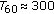 ?ms).
?ms).

