- Research Article
- Open access
- Published:
Traffic Flow Condition Classification for Short Sections Using Single Microwave Sensor
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 148303 (2010)
Abstract
Daily observed traffic flow can show different characteristics varying with the times of the day. They are caused by traffic incidents such as accidents, disabled cars, construction activities and other unusual events. Three different major traffic conditions can be occurred: "Flow," "Dense" and "Congested". Objective of this research is to identify the current traffic condition by examining the traffic measurement parameters. The earlier researches have dealt only with speed and volume by ignoring occupancy. In our study, the occupancy is another important parameter of classification. The previous works have used multiple sensors to classify traffic condition whereas our work uses only single microwave sensor. We have extended Multiple Linear Regression classification with our new approach of Estimating with Error Prediction. We present novel algorithms of Multiclassification with One-Against-All Method and Multiclassification with Binary Comparison for multiple SVM architecture. Finaly, a non-linear model of backpropagation neural network is introduced for classification. This combination has not been reported on previous studies. Training data are obtained from the Corsim based microscopic traffic simulator TSIS 5.1. All performances are compared using this data set. Our methods are currently installed and running at traffic management center of 2.Ring Road in Istanbul.
1. Introduction
Traffic flow characteristic shows dynamical change at different time periods of the day. Many traffic incidents such as accidents, disabled cars, construction activities, high demands on traffic, and other unusual events cause this change. For dealing with these unstable traffic problems, traffic conditions should be clarified. Mainly there exist three different major traffic conditions: "Flow Traffic," "Dense Traffic," and "Congested Traffic". Clarification of them requires careful/detailed examination of the flow parameters of speed, volume, and occupancy (SVO).
Accurate interpretation of SVO supports traffic management centers to make proper decision on directing the traffic to the less intensive roads. Hence, the response time for intervention in an incident will be reduced.
Measurement methods for obtaining SVO have changed for the last 60 years of the span (i.e., especially the last 40 years with the rapid rise in the number of freeways). Indeed, they are still changing [1]. Some of them are
-
(i)
measurement at a point,
-
(ii)
measurement over a short section (about 10?meters),
-
(iii)
measurement over a length of road (at least 0.5?km),
-
(iv)
measurement with mobile observer in the traffic stream,
-
(v)
measurement with multiple simultaneous mobile vehicles, as part of ITS (Intelligent Transportation Systems).
Although all measurement methods above produce speed and volume of SVO, the only method producing occupancy (i.e., the percentage of unit time that the detection zone of the instrument is occupied by vehicles) is the measurement over a short section [1].
Detectors used for short section measurement can be based on inductive loop (IL), microwave, radar, photocell, ultrasonic, and analog/digital camera technologies [1]. Since the quick and effortless installation is possible only on IL technology, we have used Radio Transmissions Microwave Sensor-based (RTMS) IL detector. We have collected SVO parameter values at different times of day by using RTMS-IL.
The collected SVO data is analyzed through our three distinct novel approaches to classify traffic flow as "Flow", "Dense", or "Congested". These approaches are estimating error prediction for multiple linear regression analysis, two improved variants of support vector machines (SVM), and backpropagation neural network. First two methods are linear classifiers, whereas NN is non-linear.
In Section 2, the contributions of our paper will be given in the related works. Then, background is presented. In the Section 4, all details about the proposed study are going to be given. Section 5 summarizes experimental results. Finally, conclusion is given.
2. Related Works
Flow theory has been tried to analyze traffic through the speed, volume, and the vehicular concentration parameters.
Temporal vehicular concentration named as occupancy can be measured only over a short section (i.e., shorter than the minimum vehicle length). So, this parameter becomes unmeaning for long section measurements.
Density as an alternative vehicular concentration has been a part of traffic measurement since 1930's. It depicts the number of vehicles over a long section (i.e., one mile or kilometer) in contrast to occupancy.
Although vehicular concentration encompasses both density andoccupancy parameters, indeed, it would be fair to say that the majority opinion is in favor of using density during the evolution of traffic flow theory.
However, a minority view has intended to use occupancy in theoretical works. Although there are well-defined facts put forward by the majority for the continued use of density, the minority also propounds major reasons for making more use of occupancy. The most crucial reason among them can be given as density (i.e., vehicles per length of road) ignores the effects of vehicle length and traffic composition. Occupancy, on the other hand, is directly affected by both of these variables and therefore gives a more reliable indicator of the amount of a road being used by vehicles.
First mathematical model-based on speed, volume, and density variables had been developed by Greenshild in mid 1930s [2] using the aerial photographs. In his work, relationship between speed and density is introduced relying on simple linear regression approach.
After World War II, with the tremendous increase in use of automobiles and the expansion of the highway system, there was also a surge in the study of traffic characteristics and the development of traffic flow theories. In 1950's, theoretical developments based on a variety of approaches, such as car-following, traffic wave theory (hydrodynamic analogy), and queuing theory has emerged. Some of the seminal works of that period include the works by Reuschel (1950) [3–5], Wardrop (1952) [6], Pipes (1953) [7], Lighthill and Whitham (1955) [8], Newell (1955) [9], Webster (1957) [10], Edie and Foote (1958) [11], Chandler et al. (1958) [12], and other papers by Herman et al.
Reuschel and Pipes offered a microscopic traffic model that identifies the linear dependency between the speed of a vehicle and the distance between the vehicles in a single lane. The models described by Reuschel and Pipes were reasonable in concept, but no experimental verification of their conclusions was pursued for many years [13].
Wardrop's theory was based on two major principles. The first one was stating that travel times between the same origin and destination pairs for any used routes are less than or equal to the travel times for all unused routes. This is referenced as Dynamic User Equilibrium (DUE) in the literature and used for large-scale networks. Diverting traffic with DUE is inefficient and difficult-to-implement system optimum (i.e., min. average travel time) [14]. The second one aims at minimizing both the total travel times and average travel times for all assigned routes for all drivers on the whole network. However, individual choice of drivers was by no means guaranteed to satisfy this principle and in most cases did not [13].
A few years later, Lighthill and Whitham (L-W) together set out the first comprehensive theory of kinematic waves. In L-W traffic model, there exists correlation between traffic flow (cars/hour) and traffic density (cars/mile) [8]. Propagation of shock waves, generated by traffic transitions from one steady state to another, was also determined by L-W model. Nevertheless, this model was viable only for describing the density changes. Unfortunately, the model produces larger densities exceeding the possible maximum vehicle density.
Greenberg improved the existing mathematical models by adding the nonlinearity into the model structure [15]. He treats the traffic stream as a continuous fluid and derives the relations between speed, density, and flow by fluid dynamics.
The distinction of free (i.e., non-congested) and congested flow on the speed-density model was carried out by Eddie [16] and Underwood [17] and was investigated in an important empirical test by Drake et al. [18].
Athol [19] suggested using the occupancy rather than the density for the flow-concentration works, however his suggestion became popular one decade later.
Speed, flow, and occupancy (SFO) relationships have been studied at the free flow level by Hurdle and Datta [20], Persaud and Hurdle [21], F. L. Hall and L. M. Hall [22], Banks [23], Smith et al. [24], Hall et al. [25], and Wemple et al. [26]. Also, SFO have been studied at congested flow level and by Hall and Montgomery [27], Zhou and Hall [28], and Banks [29, 30].
SVMs are usually employed for incident detection algorithms identifying the anomalies of traffic flow model using single or two sensors [31]. The process for determining the presence of an incident is twofold. The first is a determination of congestion (exits/not-exists), one of the states we also want to identify. Next is the binary analysis of type of congestion (incident occurred/not-occurred). Past researches and applications usually tend to use the traffic descriptors of two traffic sensors as their input parameters for incident detection with SVM methods.
In ITS, neural networks can be found on the areas like vehicle detection, road detection, and single loop vehicle type classification [32, 33]. Rarely some work related with traffic flow control can be found and they are also not well defined [34].
All retrospective researches so far show the binary relationships between the traffic parameters such as flow rate and occupancy (FR-O), flow rate and speed (FR-S), speed and occupancy (S-O) at congested or flow levels. Traffic status is assessed according to these binary relationships or by inspecting only one parameter (like speed) rather than examining all of them.
The first contribution of this paper to the traffic studies is focusing on another major traffic flow level ignored in earlier researches called dense flow level. All the previous works studies congested and flow traffic levels.
The second contribution of the paper is that no one in the earlier works is based on "single sensor" (i.e., all of them used double sensor placed within some distance) with using SVO triplets (i.e., triple relations of traffic parameters).
The third one is our new approach of "estimation with error prediction" for multiple-linear regression.
The fourth and most important one is our novel algorithms of "Multiclassification with One-Against-All" and "Multiclassification with Binary Comparison" as variants for support vector machine (SVM) classifier for the traffic flow model.
The final contribution is that none of the earlier works uses neural network model to classify the traffic control by short section with single ILD.
3. Background
One of the short section detectors, RTMS, is capable of producing some kind of traffic parameters periodically for each lane on the freeway. These parameters are volume, speed, and occupancy.
-
(i)
Volume shows the count of total vehicles passed through this short section for one period.
-
(ii)
Speed shows the average speed of total cars passed through this short section for one period.
-
(iii)
Occupancy shows the sum of the time; vehicles occupy the short section divided by one period time.
3.1. Linear Multiple Regression Analysis Method as a Classifier
The objective of linear multiple regression analysis (LMRA) is to define which of the independent variables are important on predicting the model [35]. Multiple regression analysis provides a predictive equation

where,  is interception constant,
is interception constant,  are standardized partial regression coefficients (reflecting the relative impact on the criterion variable).
are standardized partial regression coefficients (reflecting the relative impact on the criterion variable).  are the metric scores (i.e., interval or ratio data) of different independent variables.
are the metric scores (i.e., interval or ratio data) of different independent variables.  is the single dependent variable structuring the model. Equation (1) actually symbolizes a linear hyper plane. The purpose of the LMRA classifier is to minimize the energy function E for each data point, defined by LMS as in (2). The parameters
is the single dependent variable structuring the model. Equation (1) actually symbolizes a linear hyper plane. The purpose of the LMRA classifier is to minimize the energy function E for each data point, defined by LMS as in (2). The parameters  and
and  are obtained from solving the partial derivatives of
are obtained from solving the partial derivatives of

for given data.
3.2. Support Vector Machine as a Classifier
Another innovative supervised pattern classifier technique SVM was first proposed by Vapnik in 1995 [36]. The formulation applied by SVM embodies the Structural Risk Minimization (SRM) principle, which has been shown to be superior to traditional Empirical Risk Minimization (ERM) principle [37]. While SRM minimizes an upper bound on the expected risk, ERM minimizes the error on the training data [38]. It is the difference which equips SVM with a greater ability to generalize, which is the goal in statistical learning. SVMs were developed to solve the classification problem (i.e., data must belong to either Class 1(+1) or Class 2( )) but recently they have been extended to the domain of regression problems [39].
)) but recently they have been extended to the domain of regression problems [39].
The decision function in (3) determines the classes of all input vectors  [where
[where  is the input and
is the input and  is the tuple indexes].
is the tuple indexes].  is fixed feature-space transformation,
is fixed feature-space transformation,  is
is  dimensional weights, and
dimensional weights, and  is bias term [40]:
is bias term [40]:

If there are multiple solutions, we should find the smallest generalization error. So, "margin" (i.e., smallest distance between decision boundary and any of the samples) should be found through [controlling the separability] [41]:

Although there are infinite number of solutions to separate hyperplanes, by maximizing the margin, Figure 1 shows only two decision functions satisfying (4).
The margin is given by the perpendicular distance to the closest point  from the data set and we wish to optimize the parameters
from the data set and we wish to optimize the parameters  and
and  in order to maximize this distance (using target
in order to maximize this distance (using target  ). Thus the maximum margin solution is found by solving
). Thus the maximum margin solution is found by solving

The dominating approach for solving multiclass problems using SVM has been based on reducing single multi class problem into multiple binary problems. For instance, a common method is to build a set of binary classifiers where each classifier distinguishes between one of the labels to the rest. This approach is a special case of using output codes for solving multi class problems [42]. However, while multi class learning using output codes provides a simple and powerful framework it cannot capture correlations between the different classes since it breaks a multi class problem into multiple independent binary problems [43].
The idea of casting multi class problems as a single constrained optimization with a quadratic objective function was introduced by Vapnik [44] and Watkins [45]. These attempts to extend the binary case are achieved by adding constraints for every class and thus the size of the quadratic optimization is proportional to the number of categories in the classification problems. The result is often a homogeneous quadratic problem which is hard to solve and difficult to store. The idea of breaking constrained optimization problem into smaller problems was extended by Joachims [46]. Multiple class problems were then discussed by Schölkopf [47]. Today's panorama of SVM is well summarized by Cristianini [48] and more completely by Schölkopf and Smola [49].
3.3. Backpropagation Neural Network as a Classifier
Artificial neural networks (ANN) are used to serve two important functions as pattern classifiers and as nonlinear adaptive filters. Figure 2 gives a brief overview about the ANN architecture for proper pattern classification [50, 51]. Since the data is not guaranteed to be linearly separable (i.e., overlapped), three-layered Backpropagation NN (BPNN) architecture is chosen in this paper as classifier. This type of architecture does not need any prior knowledge about data (i.e., exemplar pattern initialization). Since there is no need for distribution of the data (for fault-tolerance), asynchronous update in weights and self-classification, BPNN is suitable as supervised classifier [32, 50]. In Figure 3, simple three-layered BPNN is indicated.
Classification interpretation of ANN model selecyion [ 51 ].
In our paper work, we used alternative learning methods for comparing the performances. They are Gradient Descent with Momentum (gdm), Conjugate Gradient Descent (cgd), Scaled Conjugate Gradient (scg), and Levenberg-Marquardt Gradient Descent with momentum and Scaled Conjugate Gradient. In [52], you can find algorithms and related details about the formulation and theory about these learning methods.
4. Proposed Method
4.1. Data
For each traffic condition, different values and types of data can be acquired through the FHWA's (Federal Highway Agency) TSIS 5.1 software (i.e., a CORSIM-based microscopic traffic simulation tool). Differentiation of data is supplied by configuring simulation tool parameters such as distribution function of generated traffic, lane speeds, car distances, and incident creation intervals.
Each ILD sensors generates speed, volume, and occupancy parameters values for configurable one period of time (i.e., 60 seconds) for each lane on the freeway.
4.1.1. Congested Condition
Congested traffic condition can be observed by creating long-term incidents along the freeway. According to the number of lanes they occupy, incidents can be assorted. In our study, kinds of incident scenarios are created for four-lane freeway. The sensors are placed 100 feet upstream from the incident point. As seen in Figure 4 occupancy reaches the maximum values, whereas both speed and volume reach the minimum values.
4.1.2. Flow Condition
In order to generate the flow traffic condition, CORSIM's average speed input is determined from high values (i.e., 90 km/h) and no incidents are created. Figure 5 illustrates the flow condition. It is clear from the figure that, when the speed is high and volume is low, the occupancy approximately reaches to zero. Under the low speed and high volume conditions, occupancy rises but never reaches to the maximum value.
4.1.3. Dense Condition
Dense traffic condition can be identified by generating low speed values, short-term incidents, and decreased distances between the cars in traffic. This condition is observed between the flow and congested conditions. As seen in Figure 6 the occupancy never reaches to min or max values.
4.2. Multiple Regression Analysis
There exist two significant facts through the basis of this method. The prior one says it is obvious that occupancy approximates to zero whether the average speed of vehicles approximates to infinity in flow traffic condition or not. On the contrary, occupancy goes to maximum value when speed approximates to zero in congested traffic flow condition.
It is also obvious that, until the volume reaches its maximum, occupancy is also increasing. After the maximum, the volume is going to be monotonically decreasing whereas occupancy is still increasing.
Under these circumstances, in flow traffic condition more volume leads to more occupancy. However, in congested traffic flow, the less volume observed leads to more occupancy.
According to the facts mentioned above, occupancy is dependent both on speed and volume.

Equation (6) is not viable in real world affairs. Once the traffic seems to be in congested, both speed, and volume can show the zero, although occupancy approaches to maximum. Unless the vehicles exist along the freeway (i.e., flow condition), speed, volume, and also the occupancy indicate zero. A linear dependency of SVO for each traffic condition with respect to the discrepancy are modified from (6) as in (7). For each flow condition a,  and β
2
parameters are different,
and β
2
parameters are different,

4.2.1. Regression Planes
Using the CORSIM data,  ,
,  , and
, and  values for each traffic condition are calculated using LMS (Least Mean Squares) method. The obtained results can be tracked through following subtitles.
values for each traffic condition are calculated using LMS (Least Mean Squares) method. The obtained results can be tracked through following subtitles.
(a) Congested condition. The plane evaluated for congested traffic is depicted in Figure 7 and its equation is in

Through the crosschecking (8), it can easily be seen that occupancy reaches max (98.2) when the speed and volume are marked as zero. This verifies the expectations of the real traffic condition.
(b) Flow Condition. Figure 8 shows the plane obtained from the flow traffic. Its equation is defined as

In real traffic, if no car is detected on the freeway during the time period, detectors will produce the occupancy as 0 whereas speed and volume also share the same value. Through the crosschecking (9), it can easily be seen that occupancy reaches min (0.05) when the speed and volume are marked as zero. This verifies the expectations of the real traffic condition.
(c) Dense Condition. Figure 9 depicts the dense traffic flow condition's regression plane. Linear equation of the plane can be defined as

(d) Combined Data and Regression Planes. Data and regression planes of all traffic conditions are shown in Figure 10.
Three different methods are applied, respectively, for classification of traffic conditions using linear regression.
(1) Using Analytic geometry (AG). From the CORSIM simulation, regression planes are defined for each traffic conditions. AG calculates the distances between all data points and each plane. The result (i.e., nearest plane) supplies us to infer the class (status) of current traffic.
From (8), we can obtain (11) for congested traffic as

From (9), we can obtain (12) for flow traffic as

From ((10), we can obtain (13) for dense traffic as

(2) Estimating Occupancy without Error Prediction (EO). In EO, linear regression (6) is used and error is assumed as zero. Using this assumption occupancy estimator can be calculated for each simulated traffic condition (8), (9), (10) using the real speed and real volume. After acquiring these estimators, they are compared with the real occupancy. The one nearest to real occupancy becomes the result of our traffic flow condition.
(3) Estimating Occupancy with Error Prediction (EOwEP): Another method for finding the traffic flow class is extended version of EO. This method calculates occupancy estimators by adding the predicted error values.
EOwEP depends on the training data values and their residuals. Nearest point is found by measuring L2 distance between real traffic data point and CORSIM simulated data points from each traffic condition. The residual of the found point is assumed to approximate our error. As a result, occupancy estimator for that condition can be determined. So the obtained equation as

where i is the nearest point, found by (15), to the real data point among the congested training data points

4.3. Support Vector Machines
As mentioned in background, SVM is generally applied to binary classification problems. Since the addressed problem is mapping the input data into one of three flow conditions, SVM can be seen inapplicable at first. However, without changing its calculation style, SVM can also be used in multiclassification problems. The idea lays behind multi classification is just using more than one SVM and classifing the data according to the outputs of multiple SVMs. We use our two novel approaches for Multiple SVM.
Multiclassification with One-Against-All Method (OAAM). The designated architecture (our novel approach) for this method is composed of three SVMs. Each SVM represents one of the traffic flow conditions. Detector values can be fed into each SVM, respectively. The bipolar output ["+1" (Class 1), " " (Class 2)] indicates if the input data belongs to this SVM or not.
" (Class 2)] indicates if the input data belongs to this SVM or not.
Algorithm 1
BPNN Algorithm;
-
(i)
Initialize weights (v i,j , w j,k ) with small random values
-
(ii)
Broadcast the input data to the input layer x i
Feed-forward phase is starting here;
-
(i)
Calculate the hidden layer unit signals
("f" is sigmoid function in our work)


-
(ii)
Calculate the output unit signal
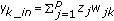
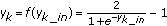
Backpropagation phase is starting here;
-
(i)
Calculate the residual. By using expected value for output signal (t k ).
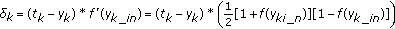
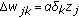
where a is learning rate. In the learning phase,
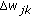 is updated according to learning rule.
is updated according to learning rule. -
(ii)
Then calculate reflectance of the residuals and propagate it to the input weights.
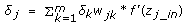
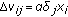
-
(iii)
All weights are updated with learning rule (i.e., gdm/scg).

-
(iv)
Test the stopping condition (i.e., reaching to "goal"; predefined Mse —mean square error- of the total residuals)
For modeling OAAM, data is acquired from TSIS 5.1. Decision is made through. "KKT (Karush-Khun-Tucker method for minimizing Quadratic Problem solution for SVM) [45] ".
[45] ".

(a) Congested SVM (C-SVM). In the training, C-SVM target is trained with "+1" whereas the other SVM targets are trained with " ". Plane for C-SVM can be shown in Figure 11. Its equation is
". Plane for C-SVM can be shown in Figure 11. Its equation is

(b) Dense SVM (D-SVM). In the training, D-SVM target is trained with "+1" whereas the other SVM targets are trained with " ". Plane for D-SVM can be shown in Figure 12. Its equation is
". Plane for D-SVM can be shown in Figure 12. Its equation is

(c) Flow SVM (F-SVM). In the training, F-SVM target is trained with "+1" whereas the other SVM targets are trained with " ". Plane for F-SVM can be shown in Figure 13. Its equation is in (19);
". Plane for F-SVM can be shown in Figure 13. Its equation is in (19);

After training is done, each member of Multiple-SVMs has its own linear planes for OAAM. In order to get the correct class of the queried data is just easy as to look at the responses of each SVMs. The "+1" response of the SVM clarifies the class of the data. For instance if F-SVM's response is "+1" (i.e., the others are expected as " ") then the class of the data belongs to flow traffic.
") then the class of the data belongs to flow traffic.
However, this is not sufficient alone. Following cases must be taken into account and supplemented approaches must be applied in these conditions.
-
(i)
If at least two SVMs produce output "+1", then the one with the longest L2 distance from data point to its own SVM plane can be picked out. Since the furthest distance from the data point to plane exposes the stricter and more accurate data for current traffic flow condition, we choose the furthest one.
-
(ii)
If all SVMs produce output "
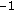 ", the one with the shortest L2 distance to SVM plane must be chosen. Producing output "–1" implies that the data does not belong to the current SVM's traffic condition. Since, the shortest distance from data point to SVM plane is the nearest one to "+1" (Class 1), we can pick this SVM out as our desired class.
", the one with the shortest L2 distance to SVM plane must be chosen. Producing output "–1" implies that the data does not belong to the current SVM's traffic condition. Since, the shortest distance from data point to SVM plane is the nearest one to "+1" (Class 1), we can pick this SVM out as our desired class.
Multiclassification with Binary Comparison (BC)
Our other novel approach applied to classify our data is again composed of three SVMs. However, it can be distinguished from the OAAM method by its architecture. In BC method, each SVM is responsible for the following binary combinations, respectively; (Congested, Dense), (Congested, Flow), and (Flow, Dense). This multi classification method depends on basic voting principle. There exist three candidates (i.e., Congested, Flow, and Dense traffic conditions) and three voters (each SVM). The one among the candidates wins the election if it gets the most votes from voters.
(a) Congested-Dense (CD-SVM). In the training, CD-SVM target "+1" indicates that data belongs to Class 1 (i.e., congested traffic). The other alternative of " " indicates that the data belongs to Class 2 (i.e., dense traffic). So the voter gives its vote to Congested candidate if its output equals "+1". In adverse condition, it gives to Dense candidate. Figure 14 shows the decision plane for CD-SVM. The plane equation is
" indicates that the data belongs to Class 2 (i.e., dense traffic). So the voter gives its vote to Congested candidate if its output equals "+1". In adverse condition, it gives to Dense candidate. Figure 14 shows the decision plane for CD-SVM. The plane equation is

(b) Congested-Flow SVM (CF-SVM). In the training, CF-SVM target "+1" indicates that data belongs to congested traffic. The other alternative of " " indicates that the data belongs to flow traffic. Figure 15 shows the decision plane for CF-SVM. The plane equation is
" indicates that the data belongs to flow traffic. Figure 15 shows the decision plane for CF-SVM. The plane equation is

(c) Flow-Dense SVM (FD-SVM). In the training, FD-SVM target "+1" indicates that data belongs to flow traffic. The other alternative of " " indicates that the data belongs to dense traffic. Figure 16 shows the decision plane for FD-SVM. The plane equation is
" indicates that the data belongs to dense traffic. Figure 16 shows the decision plane for FD-SVM. The plane equation is

A supplemented way must be found for handling the situation when all candidates have the equal vote. Using the longest distance from data point to each SVM's plane will give us the most accurate class for that data point. Then the SVM with the longest distance will choose the leader class.
Backpropagation Neural Network Architectures
The network architecture in our work is selected as three-layered backpropagation neural network (BPNN). three groups of data are used as input. The first group is fed into the network as training data set. The next one is used as verification data set. The last one is used as query set (i.e., test set) to measure the classification performance of the neural net.Training data set is obtained from TSIS 5.1 simulator. This data is verified through the verification set also gathered from the simulator. The test set is gathered from single sensor planted on the 2.Ring road in Istanbul. Test set indicates real data. Our model is trained and verified through the simulated data and tested with real traffic information.In the learning phase we have used gradient descent with momentum (Gdm) update function in (23) (i.e., learning rule). This base rule is used for all architectures

In the learning phase, we have used the algorithms of only Gdm, Levenberg-Maquardt with Gdm and Scaled Conjugate Gradient with Gdm [52]. Matlab 7.6.0 (Rev.2008a) Neural Network Toolbox where our related work algorithms and learning rules are ready is used.
We have used default max iteration as 1000, Mse goal value as  , and verification iteration count as 6. The network architecture is performed as three-layered models of 3-10-3, 3-20-3, and 3-50-3. Since one hidden layer usage is almost identical with two hidden layered architecture, we prefer to use single hidden layer model. For the connections lying between Input/Hidden Layers are trained with LogSig or PureLin activation functions. LogSig activation function normalized the input and applies Sigmoid. Pure Linear activation function transfers input to hidden.We give the performance analysis of our neural net architectures in Table 1. Gray labeled values are average performances obtained from 100 runs of neural net models. According to the average performances, our 3-20-3 backpropagation model gives the best result for classification.
, and verification iteration count as 6. The network architecture is performed as three-layered models of 3-10-3, 3-20-3, and 3-50-3. Since one hidden layer usage is almost identical with two hidden layered architecture, we prefer to use single hidden layer model. For the connections lying between Input/Hidden Layers are trained with LogSig or PureLin activation functions. LogSig activation function normalized the input and applies Sigmoid. Pure Linear activation function transfers input to hidden.We give the performance analysis of our neural net architectures in Table 1. Gray labeled values are average performances obtained from 100 runs of neural net models. According to the average performances, our 3-20-3 backpropagation model gives the best result for classification.
5. Experimental Work
Turkey General Directorate of Highways has carried out works in managing traffic in Istanbul hence traffic management center is planned to be opened at the end of December 2007. The system is installed by Turkey's leading electronics company ASELSAN Inc. In Istanbul traffic management system, microwave radar type detectors are used for occupancy, speed, and traffic volume measurements. There exist almost 30 radio transmission microwave sensors along the 2.Ring Road. The measurements recorded at critical points on the road are transmitted periodically to the management center [53].
Occupancy, speed, and traffic volume measurements are both recorded in the database, and the traffic status according to these measurements is mapped to color codes and displayed on a large screen. Whenever any congested state or dense state occurs along the road, alarms with severity levels are generated and the operators are informed. Information regarding the traffic status is also displayed on LED-based Variable Message Signs (VMS) on the road.
During one day, data from 7 different microwave sensors is acquired every 60 seconds periodically. Occupancy, volume and speed measurements are shown in Figure 17. Videos from the traffic surveillance cameras, which are capable of watching the places that microwave sensors are installed, are also captured in order to synchronize them with the sensors measurements. Then, measurements are grouped as congested, dense and flow according to these videos. [We have used training data set of total size 18.000 x 3 (i.e., each traffic condition has balanced data subset size of 6000 x 3) and we have used testing data set of total size 55.000 x 3, and 3 indicates SVO values]. These data sets are used to for the Table 2.
6. Conclusion
Eight methods discussed above have applied the one day data captured from 7 sensors on 2.Ring Road in Istanbul. Their performance for each traffic condition can be seen in Table 2.
Although our novel approaches OAAM and BC for Multiple SVM have good performances, our BPNN architecture of 3-20-3 with SCG (3-20-3) is better than all other seven methods. As a result of this comparison, this method has chosen and installed for the evaluation of traffic condition in Istanbul traffic management center (at Istanbul 2.Ring road).
According to the result it calculates, our algorithm colors the road map for each status changes on GIS projection screens. Once congested level is detected, it produces an alarm with high severity to inform the operators. Nevertheless, dense level also creates alarm with lower severity. After verification of this assessment by operator, VMS can be supplied by messages to inform drivers about the road flow condition.
References
Hall FL: Traffic stream characteristics. USA Transportation Research Board. Traffic Flow Theory, A State of the Art Report 1992.
Greenshields BD: A study of traffic capacity. Highway Research Board Proceedings 1935, 14: 448-477.
Reuschel A: Fahrzeugbewegungen in der Kolonne. Oesterreichisches Ingenieur 1950a, 4(3/4):193-215.
Reuschel A: Fahrzeugbewegungen in der Kolonne bei gleichformig beschleunigtem oder verzogertem, Leitfahrzeug. Zeitschrift des Oesterreichischen Ingenieurund Architekten-Vereines 1950, 95(9):59-62.
Reuschel A: Fahrzeugbewegungen in der Kolonne bei gleichformig beschleunigtem oder verzogertem, Leitfahrzeug. Zeitschrift des Oesterreichischen Ingenieurund Architekten-Vereines 1950, 97-98(10):73-77.
Wardrop JG: Some theoretical aspects of road traffic research. Proceedings Institute of Civil Engineers, Part II 1952, 1: 325-378.
Pipes LA: An operational analysis of traffic dynamics. Journal of Applied Physics 1953, 24(3):274-281. 10.1063/1.1721265
Lighthill MJ, Whitham GB: On kinematic waves. II. A theory of traffic flow on long crowded roads. Proceedings of the Royal Society of London 1955, 317-345.
Newell GF: Mathematical models for freely-flowing highway traffic. Journal of the Operations Research Society of America 1955, 3: 176-186.
Webster FV: Traffic signal settings. In Road Research Technical. Road Research Laboratory, London, UK; 1958.
Edie LC, Foote RS: Traffic flow in tunnels. Proceedings of Highway Research Board 1958, 37: 334-344.
Chandler RE, Herman R, Montroll EW: Traffic dynamics: studies in car following. Operations Research 1958, 6: 165-184. 10.1287/opre.6.2.165
Gazis DC: The origins of traffic theory. Operations Research 2002, 50(1):69-77. 10.1287/opre.50.1.69.17776
Correa JR, Schulz AS, Stier-Moses NE: Selfish routing in capacitated networks. Mathematics of Operations Research 2004, 29(4):961-976. 10.1287/moor.1040.0098
Greenberg H: An analysis of traffic flow. Operations Research 1959, 7: 79-85. 10.1287/opre.7.1.79
Edie LC: Car following and steady-state for non-congested traffic. Operations Research 1961, 9: 66-76. 10.1287/opre.9.1.66
Underwood RT: Speed, volume, and density relationships: quality and theory of traffic flow. Yale Bureau of Highway Traffic 1961, 141-188.
Drake JS, Schofer L, May AD: A statistical analysis of speed density hypotheses. Highway Research Record 1967, 154: 53-87.
Athol P: Interdependence of certain operational characteristics within a moving traffic stream. Highway Research Record 1965, 72: 58-87.
Hurdle VF, Datta PK: Speeds and flows on an urban freeway: some measurements and a hypothesis. In Transportation Research Record 905. TRB, NRC, Washington, DC, USA; 1983:127-137.
Persaud BN, Hurdle VF: Some new data that challenge some old ideas about speed-flow relationships. In Transportation Research Record. Volume 1194. TRB, NRC, Washington, DC; 1988:191-198.
Hall FL, Hall LM: Capacity and speed flow analysis of the Queue in Ontario. In Transportation Research Record. Volume 1287. TRB, NRC, Washington, DC, USA; 1990:108-118.
Banks JH: Freeway speed-flow concentration relationships: more evidence and interpretations. In Transportation Research Record. Volume 1225. TRB, NRC, Washington, DC, USA; 1989:53-60.
Smith WS, Hall FL, Montgomery FO: Comparing the speed-flow relationship for motorways with new data from the M6. Transportation Research Part A 1996, 30(2):89-101. 10.1016/0965-8564(95)00015-1
Hall FL, Hurdle VF, Banks JH: Synthesis of recent work on the nature of speed-flow and flow-occupancy (or density) relationships on freeways. In Transportation Research Record. Volume 1365. TRB, NRC, Washington, DC, USA; 1992:12-18.
Wemple EA, Morris AM, May AD: Freeway capacity and level of service concepts. Proceedings of International Symposium on Highway Capacity, 1991, Karlsruhe, Germany 439-455.
Hall FL, Montgomery FO: Investigation of an alternative interpretation of the speed-flow relationship for U.K. motorways. Traffic Engineering and Control 1993, 34(9):420-425.
Zhou M, Hall FL: Investigation of speed-flow relationship under congested conditions on a freeway. Transportation Research Record 1999, (1678):64-72.
Banks JH: Investigation of some characteristics of congested flow. Transportation Research Record 1999, (1678):128-134.
Banks JH: Review of empirical research on congested freeway flow. Transportation Research Record 2002, (1802):225-232.
Yuan F, Cheu RL: Incident detection using support vector machines. Transportation Research Part C 2003, 11(3-4):309-328. 10.1016/S0968-090X(03)00020-2
Oh C, Ritchie SG: Recognizing vehicle classification information from blade sensor signature. Pattern Recognition Letters 2007, 28(9):1041-1049. 10.1016/j.patrec.2007.01.010
Mussa R, Kwigizile V, Selekwa M: Probabilistic neural networks application for vehicle classification. Journal of Transportation Engineering 2006, 132(4):293-302. 10.1061/(ASCE)0733-947X(2006)132:4(293)
Vlahogianni EI, Golias JC, Karlaftis MG: Short-term traffic forecasting: overview of objectives and methods. Transport Reviews 2004, 24(5):533-557. 10.1080/0144164042000195072
Vapnik VN: The Nature of Statistical Learning Theory. Springer, New York, NY, USA; 1995.
Gunn SR, Brown M, Bossley KM: Network performance assessment for neurofuzzy data modeling. Intelligent Data Analysis, Lecture Notes in Computer Science 1997, 1208: 313-323.
Gunn SR: Support vector machines for classification and regression. Image Speech and Intelligent System Research Group, University of Southampton, Southampton, UK; 1998.
Vapnik V, Golowich S, Smola A: Support vector method for function approximation, regression estimation, and signal processing. In Advances in Neural Information Processing Systems. Volume 9. MIT Press, Cambridge, Mass, USA; 1997:281-287.
Abe S: Support Vector Machines For Pattern Recognition. 2005.
Bishop C: Pattern Recognition and Machine Learning. Springer, New York, NY, USA; 2007.
Dietterich TG, Bakiri G: Solving multiclass learning problems via error correcting output codes. Journal of Artificial Intelligence Research 1995, 2: 263-286.
Crammer K, Singer Y: On the algorithmic implementation of multiClass kernel based vector machines. Journal of Machine Learning Research 2001, 2: 265-292.
Vapnik VN: Statistical Learning Theory. John Wiley & Sons, New York, NY, USA; 1998.
Weston J, Watkins C: Support vector machines for multi-class pattern recognition. Proceedings of the 7th European Symposium on Artificial Neural Networks, 1999
Joachims T: Making large-scale support vector machine learning practical. In Advances in Kernel Methods—Support Vector Learning. Edited by: Scholkopf B, Burges C, Smola A. MIT Press; 1998.
Schölkopf B: Statistical Learning and Kernel Methods. Microsoft Research; 2000.
Cristianini N, Taylor JS: An Introduction to Support Vector Machines, and Other Kernel-Based Learning Methods. Cambridge University Press, Cambridge, UK; 2000.
Schölkopf B, Smola A: Learning with Kernels. MIT Press, Cambridge, Mass, USA; 2002.
Fausett L: Fundementals of Neural Networks: Architectures, Algorithms and Applications. Prentice-Hall, Upper Saddle River, NJ, USA; 1994.
Jain AK, Mao J, Mohiuddin KM: Artificial neural networks: a tutorial. Computer 1996, 29(3):31-44. 10.1109/2.485891
Haykin S: Neural Networks: A Comprehensive Foundation. Prentice-Hall, Upper Saddle River, NJ, USA; 1998.
Dorken E, Barut DM, Oranç BT: Integrated electronic tolling and traffic management on Turkish highways. Proceedings of 12th World Congress on Intelligent Transport Systems, 2005, San Francisco, Calif, USA 2901.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cinsdikici, M.G., Memiş, K. Traffic Flow Condition Classification for Short Sections Using Single Microwave Sensor. EURASIP J. Adv. Signal Process. 2010, 148303 (2010). https://doi.org/10.1155/2010/148303
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/148303












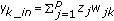
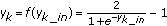
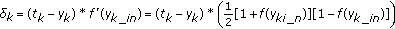
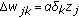
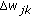 is updated according to learning rule.
is updated according to learning rule.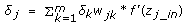
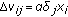



 ", the one with the shortest L2 distance to SVM plane must be chosen. Producing output "–1" implies that the data does not belong to the current SVM's traffic condition. Since, the shortest distance from data point to SVM plane is the nearest one to "+1" (Class 1), we can pick this SVM out as our desired class.
", the one with the shortest L2 distance to SVM plane must be chosen. Producing output "–1" implies that the data does not belong to the current SVM's traffic condition. Since, the shortest distance from data point to SVM plane is the nearest one to "+1" (Class 1), we can pick this SVM out as our desired class.



