- Research Article
- Open access
- Published:
A Conditional Random Field Approach to Unsupervised Texture Image Segmentation
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 167942 (2010)
Abstract
An unsupervised multiresolution conditional random field (CRF) approach to texture segmentation problems is introduced. This approach involves local and long-range information in the CRF neighbourhood to determine the classes of image blocks. Like most Markov random field (MRF) approaches, the proposed method treats the image as an array of random variables and attempts to assign an optimal class label to each. While most MRFs involve only local information extracted from a small neighbourhood, our method also allows a few long-range blocks to be involved in the labelling process. This alleviates the problem of assigning different class labels to disjoint regions of the same texture and oversegmentation due to the lack of long-range interaction among the neighbouring and distant blocks. The proposed method requires no a priori knowledge of the number and types of regions/textures.
1. Introduction
Image segmentation is essentially the first step toward many image analysis and computer vision problems. It is usually formulated as an optimization problem, in which the image in question is partitioned into a number of homogeneous regions, each characterized by a unique set of features [1]. Its applications can be found in a wide variety of areas, such as biomedical image processing [2–4], remote sensing [5–7], target identification and tracking [8], anomaly detection [9], video analysis [10], scene segmentation [11, 12], sonar imagery [13], surveillance [14], land use [15–17], and image database retrieval [14, 18]. However, segmenting textured images is not a trivial task for various reasons.
-
(i)
Firstly, textures comprise primitives/textons and tiny edges (intensity fluctuations), which can cause false responses in conventional edge detectors, while texture boundaries do not appear as conventional edges and therefore often go undetected by conventional edge detectors.
-
(ii)
Secondly, another major difficulty in texture segmentation arises from the fact that texture is a regional property [19] rather than a pixel property. The information in a single pixel is only the intensity or colour. By contrast, we need to cover a reasonably large area of pixels in order to extract meaningful texture features. If we take a big area of a textured image into consideration, we get high confidence in the class of the texture. However, we lose the resolution in which the texture boundary may be if the area in question contains more than one class of textures. On the other hand, if we confine the analysis to a smaller area, the confidence in the position of texture boundaries increases at the expense of the certainty of texture class. This phenomenon, known as "class-boundary uncertainty" [1], suggests that information at multiple resolutions or scales has to be fused in some way for effective segmentation. This motivates the adoption of the various multiresolution approaches in many works [20–23].
-
(iii)
Thirdly, to be practicable in a wide variety of applications, it is desirable that a segmentation algorithm should work without human supervision or intervention. To achieve this objective, the algorithm should not rely on the user to provide knowledge about the number of texture classes and the types of textures contained in the target image [1]. The latter means that it is preferable not to have a training phase before the algorithm is used. This requirement is sensible because if the training phase were needed, then when textures outside the training set appear in the images to be segmented, the algorithm would have difficulty identifying them.
-
(iv)
Moreover, an intelligent algorithm should not only be able to segment images into regions, but also be capable of classifying disjoint regions of the same texture into the same class [15, 16]. For example, an algorithm capable of segmenting an aerial image with two disjoint urban areas from their woodland background and assigning the same class label to the two urban areas is certainly superior to an algorithm only capable of segmenting the image into three regions.
The motivation of this work is to develop an unsupervised algorithm, which is capable of meeting these requirements.
2. Related Work
In the last few decades, a wide variety of methods, such as fuzzy clustering [19, 23], watershed transform [18], active contours [24], independent component analysis [25], and morphology-based estimation [26], have been explored to solve the problem of texture segmentation. Among them, Markov random field (MRF) [1, 7, 9, 27, 28] is one of the most frequently used approaches due to the simplicity of its local characteristics (also known as Markovianity) [29]. Markovianity allows a global optimization problem to be solved locally and this is confirmed by the results reported in our recent work [1]. The approach presented in [1] is a typical combination of MRFs and simulated annealing, known as the Gibbs sampler [21]. The idea is to divide an image into a number of blocks and treat each block as a random variable to be assigned a class label depending on its own features, its neighbours' features, and class labels. When a block  is visited, the probabilities of the labels assigned to its neighbours are calculated according to a cost function. The optimal label is assigned the highest probability and the less promising labels get lower probabilities. Simulated annealing [21] is then applied so as to assign one of the labels to block
is visited, the probabilities of the labels assigned to its neighbours are calculated according to a cost function. The optimal label is assigned the highest probability and the less promising labels get lower probabilities. Simulated annealing [21] is then applied so as to assign one of the labels to block  . When the labelling process converges, the labelling result is propagated down to the next resolution level for finer segmentation. This process is repeated until a nominal bottom level is reached. Since this is a multiresolution approach, the neighbourhood includes the 4 neighbours at the same level and the parent block at one level above (except the nominal top level). By using the idea of SOIL (set of indispensable labels) reported in [30] and exploiting local feature disparities, this work requires no a priori global knowledge about the number of texture classes and the types of textures contained in the images. However, the work has the following limitations.
. When the labelling process converges, the labelling result is propagated down to the next resolution level for finer segmentation. This process is repeated until a nominal bottom level is reached. Since this is a multiresolution approach, the neighbourhood includes the 4 neighbours at the same level and the parent block at one level above (except the nominal top level). By using the idea of SOIL (set of indispensable labels) reported in [30] and exploiting local feature disparities, this work requires no a priori global knowledge about the number of texture classes and the types of textures contained in the images. However, the work has the following limitations.
-
(i)
Due to the lack of long range interaction with blocks outside the local neighbourhood and the fact that the algorithm starts with a random class label configuration, disjoint regions of the same texture are assigned different class labels. An example is shown in Figure 1(a), wherein the two disjoint regions on the right and left sides containing the same texture have been misclassified into two different classes—class 5 and 7, as shown in Figure 1(b).
-
(ii)
Again, for the same reason, large or elongated regions may be oversegmented. For example, the region in the middle of Figure 1(a) has been oversegmented into two classes with labels 2 and 9, as shown in Figure 1(b). This can be explained as follows. Given Figure 1(b) as the current label configuration, with a 4-neighbourhood system, despite the fact that sites (5, 5) and (6, 5) belong to the same region, when site (5, 5) is visited, three of its neighbours within the 4-neighbourhood system are labelled 2 while only one is labelled 9. Therefore, the probability of assigning 2 to site (5, 5) is high, while the probability of assigning label 9 will decrease as relaxation proceeds. Similarly, site (6, 5) is next to three neighbours with label 9 and only one with label 2. Therefore the probability that it will be assigned label 9 is far greater than getting assigned label 2. This kind of local "sibling competition" can lead to premature convergence at local minima in the energy landscape and consequently give rise to oversegmentation. This type of oversegmentations is more likely to occur in large or elongated regions, where different class labels may grow into subregions from different locations of the regions. When these subregions meet, sibling competition starts and spurious boundaries may form.
-
(iii)
The energy function adopted in [1] was based on the assumption that the distributions of both intraclass and interclass feature disparities of useful features are approximately Gaussian. Although this is a reasonable assumption, the accuracy of the prior model may have significant influence on the efficacy of the segmentation. The potential function, which is encoded in the energy function, is also complicated and needs to be recalculated iteratively in an iterated conditional mode (ICM) sense [29].
Theoretically, the first two limitations, due to the lack of long-range interaction, could be alleviated if the annealing schedule starts at higher temperature. However, this gain can only be obtained at the expense of convergence rate. Another possibility is to involve a larger neighbourhood to accommodate more interaction among blocks in the decision process. However, for Markov random field approaches, adopting a larger neighbourhood incurs higher computational cost. Moreover, the range of the interaction is still bounded by the neighbourhood. In its extreme case when the whole image is involved, the local characteristic of Markov random fields (Markovianity) is completely lost. Therefore, reaching out from the local neighbourhood in some way is more desirable than expanding the neighbourhoods.
As described in the next section, we propose an improved Markov random field (MRF) approach, which involves both local and long-range information in a simpler energy function, to alleviate the aforementioned limitations of our previous work [1]. The objectives of the proposed work are as follows:
-
(i)
resolving local sibling competition in order to tackle the problem of oversegmentation,
-
(ii)
labelling disjoint regions of the same texture consistently by involving long-range interaction among blocks,
-
(iii)
reducing the computational cost by simplifying the energy function and facilitating information fusion through long range interaction among blocks.
3. Multiresolution Markov Random FieldTexture Segmentation Algorithm
To avoid confusing the reader with details, we first present the whole picture of the proposed algorithm as follows.
Multiresolution Conditional Random Field Texture Segmentation Algorithm
-
(1)
Build a multiresolution pyramid conforming to a quad-tree structure.
-
(2)
Extract texture features from each image block.
-
(3)
Assign a random label to each block at the top level to form an initial label configuration.
-
(4)
For each resolution level before the nominal bottom level is reached
-
(4.1)
While not converged, for each block
-
(4.1.1)
form a voting pool,
-
(4.1.2)
calculate the energy functions of the labels of the members in the voting pool,
-
(4.1.3)
calculate the probabilities of the labels based on their energy functions,
-
(4.1.4)
assign one of the labels according the probability,
-
(4.1.1)
-
(4.2)
propagate results to the next resolution level.
-
(4.1)
In the first step of the proposed algorithm, a multiresolution framework is adopted to represent the image data at multiple scales in order to alleviate the canonical problem of class-boundary uncertainty [1, 2]. Note that in order not to complicate the symbols in the presentation of the algorithm later, we will assume that the original images are square. However, the two dimensions of the original image need not to be equal. We create an image pyramid conforming to a quad-tree structure with  resolution levels based on the original image of
resolution levels based on the original image of  pixels. Each level
pixels. Each level  consists of an array of
consists of an array of  sites/blocks of
sites/blocks of  pixels by sliding a window of
pixels by sliding a window of  pixels over the original image in
pixels over the original image in  -pixel wide steps in both horizontal and vertical directions. That is to say that the sampling windows are 50% overlapped. At the higher levels, the size of the block is larger, which gives higher resolution of texture classes but lower resolution of texture boundaries. While at lower levels, the blocks are smaller, and as a result, higher boundary resolution is gained at the expense of class resolution. At the top level (i.e.,
-pixel wide steps in both horizontal and vertical directions. That is to say that the sampling windows are 50% overlapped. At the higher levels, the size of the block is larger, which gives higher resolution of texture classes but lower resolution of texture boundaries. While at lower levels, the blocks are smaller, and as a result, higher boundary resolution is gained at the expense of class resolution. At the top level (i.e.,  ), there is only one block, which covers the whole image; therefore, the algorithm must start at a nominal top level
), there is only one block, which covers the whole image; therefore, the algorithm must start at a nominal top level  in order to carry out the segmentation task. At the bottom level (i.e.,
in order to carry out the segmentation task. At the bottom level (i.e.,  ), each block covers only one pixel, which carries no texture features. Therefore, the algorithm should stop at a nominal bottom level with
), each block covers only one pixel, which carries no texture features. Therefore, the algorithm should stop at a nominal bottom level with  .
.
Usually a complete segmentation process includes a feature extraction stage, followed by alabelling stage. At the first step of the proposed algorithm, a set of texture features is extracted from each site  as the observed data
as the observed data  . In practice, features suitable for the segmentation task are image and application dependent. Since the main purpose of this work is to propose, not a feature extraction method, but a generic labelling algorithm, we include only the mean and variance of the intensity in the feature set. However, the reader is reminded that appropriate features other than mean intensity and variance can be incorporated with the proposed labelling algorithm since the feature extraction and labelling processes are separate modules.
. In practice, features suitable for the segmentation task are image and application dependent. Since the main purpose of this work is to propose, not a feature extraction method, but a generic labelling algorithm, we include only the mean and variance of the intensity in the feature set. However, the reader is reminded that appropriate features other than mean intensity and variance can be incorporated with the proposed labelling algorithm since the feature extraction and labelling processes are separate modules.
Steps (3) and (4) carry out the segmentation task by labelling the sites in an iterative manner. At each level, the class label of each site  is treated as a random variable
is treated as a random variable  . The task of the segmentation algorithm is to assign an optimal class label
. The task of the segmentation algorithm is to assign an optimal class label  (an instance of the random variable) to each site
(an instance of the random variable) to each site  , depending on the observed data
, depending on the observed data  at
at  , the observed data
, the observed data  and class labels
and class labels  , for all sites
, for all sites  in a "voting pool",
in a "voting pool",  . This can be formulated as a random field (RF) model according to the Bayes theorem
. This can be formulated as a random field (RF) model according to the Bayes theorem

where  and
and  represent the observed data and class labels of all the sites
represent the observed data and class labels of all the sites  in
in  , respectively. That is,
, respectively. That is,  and
and  .
.  and
and  are the conditional probability distribution and prior probability distribution, respectively. Usually, the number of texture classes in the image in question is unknown to the user. To allow the algorithm to work without the user specifying the number of texture classes, at the nominal top level, each block is assigned a label randomly picked from the integer range
are the conditional probability distribution and prior probability distribution, respectively. Usually, the number of texture classes in the image in question is unknown to the user. To allow the algorithm to work without the user specifying the number of texture classes, at the nominal top level, each block is assigned a label randomly picked from the integer range  , where
, where  is the number of blocks at the nominal top level. That is, we allow the algorithm to start with a completely random label configuration. This is virtually equivalent to adopting an "infinite" label space.
is the number of blocks at the nominal top level. That is, we allow the algorithm to start with a completely random label configuration. This is virtually equivalent to adopting an "infinite" label space.
The neighbourhood system of MRF algorithms plays an important role in the segmentation process. As mentioned in the previous section, the lack of long-range interaction during the labelling processing in the algorithm of [1] is the key reason that oversegmentation occurs and that the algorithm is not able to assign the same class label to disjoint regions of the same texture; it is also one of the reasons why the algorithm's convergence rate cannot be accelerated. To involve long-range interaction, when a site  at level
at level  is being visited, in addition to its parent block
is being visited, in addition to its parent block  at level
at level  and the 4 neighbours (
and the 4 neighbours ( ,
,  ,
,  , and
, and  ) at level
) at level  , three other blocks,
, three other blocks,  ,
,  , and
, and  are also included in the voting pool
are also included in the voting pool  .
.  and
and  are selected at random, and
are selected at random, and  is the block whose feature set is most different from that of
is the block whose feature set is most different from that of  . So, the voting pool can be expressed as
. So, the voting pool can be expressed as

For example, let  denote a site appearing at coordinates
denote a site appearing at coordinates  at level
at level  . Figure 2 demonstrates that the voting pool of site
. Figure 2 demonstrates that the voting pool of site  at
at  is
is  , where
, where  is to be found in Figure 2(b), while others are to be found in Figure 2(a). Apart from the parent block and the 4 neighbours, all the other members may be different in different iterations. The most different block,
is to be found in Figure 2(b), while others are to be found in Figure 2(a). Apart from the parent block and the 4 neighbours, all the other members may be different in different iterations. The most different block,  , is the one identified from the randomly picked members during the whole labelling history. That is, in any iteration, if a voting block selected at random (i.e.,
, is the one identified from the randomly picked members during the whole labelling history. That is, in any iteration, if a voting block selected at random (i.e.,  or
or  ) is more different from
) is more different from  than the current most different block, the most different block is replaced by that voting block. Note that at the top resolution level, there is no parent block in the voting pool. In addition to playing the same role as
than the current most different block, the most different block is replaced by that voting block. Note that at the top resolution level, there is no parent block in the voting pool. In addition to playing the same role as  and
and  of introducing long-range interaction, the most different block
of introducing long-range interaction, the most different block  plays an extra role of informing the algorithm that the label associated with the most different block is to be avoided. Because of the contextual property of texture, there is no need to keep track of the most similar block for each site
plays an extra role of informing the algorithm that the label associated with the most different block is to be avoided. Because of the contextual property of texture, there is no need to keep track of the most similar block for each site  , given the fact that the 4 neighbours have already been included in the voting pool.
, given the fact that the 4 neighbours have already been included in the voting pool.
Voting pool of site  , the grey block in (a), at resolution level
, the grey block in (a), at resolution level  . The voting pool consists of the sites highlighted with bold line segments in both (a) and (b), which includes parent site
. The voting pool consists of the sites highlighted with bold line segments in both (a) and (b), which includes parent site  at level
at level  in (b), 4 neighbours at
in (b), 4 neighbours at  ,
,  ,
,  ,
,  , two randomly picked sites at
, two randomly picked sites at  and
and  , and the most different site at
, and the most different site at  .(a) Label configuration at level
.(a) Label configuration at level  (b) Label configuration at level
(b) Label configuration at level 
To allow the algorithm to segment images with arbitrary numbers of texture regions without the user specifying the number, when each block is being visited, only the class labels currently assigned to the members of its voting pool are taken as candidates. For example, when the grey site at coordinates  in Figure 2 is being visited, the candidate labels
in Figure 2 is being visited, the candidate labels  are just
are just  . The advantages of randomising the initial label configuration at Step (3) with a label space of
. The advantages of randomising the initial label configuration at Step (3) with a label space of  and using the proposed voting pool are now clear. First,globally the number of labels allowed is equal to the number of blocks
and using the proposed voting pool are now clear. First,globally the number of labels allowed is equal to the number of blocks  . That means we ensure diversity by sampling the label configuration of the whole image from a virtually infinite label space. Secondly, the computational cost is kept low because locally the optimal label of each individual block is sampled from a small space with its cardinality ≤8 because there are at most 8 members in the voting pool
. That means we ensure diversity by sampling the label configuration of the whole image from a virtually infinite label space. Secondly, the computational cost is kept low because locally the optimal label of each individual block is sampled from a small space with its cardinality ≤8 because there are at most 8 members in the voting pool  . The cardinality of
. The cardinality of  will decrease in due course as the homogeneous regions emerge. In our previous example, the cardinality is only 3. Although starting from a random initial label configuration, a unique optimal label for each texture class can be quickly identified through the interaction with the members of the voting pool. It should be noted that, at lower resolution levels, a random label that is not assigned to any site can be included as a candidate in order to encourage small regions to emerge. However, texture class certainty is lower at lower resolution levels and texture may comprise recursive patterns/textons, which can be smaller than the image blocks. Including such an unused label increases the possibility of detecting small spurious regions that are actually part of a larger and genuine texture region. Therefore, whether to include such a label as candidate is application dependent. In this work, we choose not to include it.
will decrease in due course as the homogeneous regions emerge. In our previous example, the cardinality is only 3. Although starting from a random initial label configuration, a unique optimal label for each texture class can be quickly identified through the interaction with the members of the voting pool. It should be noted that, at lower resolution levels, a random label that is not assigned to any site can be included as a candidate in order to encourage small regions to emerge. However, texture class certainty is lower at lower resolution levels and texture may comprise recursive patterns/textons, which can be smaller than the image blocks. Including such an unused label increases the possibility of detecting small spurious regions that are actually part of a larger and genuine texture region. Therefore, whether to include such a label as candidate is application dependent. In this work, we choose not to include it.
The conditional random field (CRF) model of (1) can also be expressed in Gibbs form [21] in terms of energy functions  and
and  within the voting pool
within the voting pool  as
as

where  and
and  are associated with the conditional probability distribution and prior probability distribution of (1), respectively, and
are associated with the conditional probability distribution and prior probability distribution of (1), respectively, and  is the so-called partition function, which is to serve the purpose of normalisation. By properly reformulating the two energy functions in (3), as described in [21], we obtain a new model as
is the so-called partition function, which is to serve the purpose of normalisation. By properly reformulating the two energy functions in (3), as described in [21], we obtain a new model as

where the partition function is

Like most optimisation processes, defining a feasible objective function is important, yet by no means trivial. In the proposed algorithm, the energy function  is defined as the sum of the pairwise potentials
is defined as the sum of the pairwise potentials  between site
between site  and voting members
and voting members  in
in  :
:

where the potential  is defined as
is defined as

where  is the feature disparity between sites b and
is the feature disparity between sites b and  , defined as
, defined as

and  is the estimated threshold dividing the space of feature disparities into subspaces of intra- and interclass feature disparities. To estimate
is the estimated threshold dividing the space of feature disparities into subspaces of intra- and interclass feature disparities. To estimate  for each resolution level, 300 pairs of blocks are picked at random from the same resolution level and their feature disparities are calculated. We allow a block to be paired with more than one partner. Since some pairs might belong to the same texture class and some might not, we can have two types of feature disparity: intraclass with relatively smaller value and interclass with relatively greater value. By taking the smallest and the greatest feature disparity as the initial centroids of intraclass and interclass, respectively, a trivial 2-mean clustering method is employed to partition the space of the 300 feature disparities into two clusters. Then,
for each resolution level, 300 pairs of blocks are picked at random from the same resolution level and their feature disparities are calculated. We allow a block to be paired with more than one partner. Since some pairs might belong to the same texture class and some might not, we can have two types of feature disparity: intraclass with relatively smaller value and interclass with relatively greater value. By taking the smallest and the greatest feature disparity as the initial centroids of intraclass and interclass, respectively, a trivial 2-mean clustering method is employed to partition the space of the 300 feature disparities into two clusters. Then,  of (5) can be calculated according to
of (5) can be calculated according to

where  is the greatest value in intraclass and
is the greatest value in intraclass and  is the smallest value in interclass. The feasibility of the energy function
is the smallest value in interclass. The feasibility of the energy function  and pairwise potential
and pairwise potential  is discussed as follows.
is discussed as follows.
-
(i)
The first merit is that
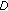 ,
, 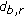 ,
, 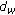 , and
, and 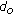 are all adaptive to the content of the image. Since the complexity of (5) is low, the computational cost of calculating the energy function defined in (4) is significantly lower than the one used in [1].
are all adaptive to the content of the image. Since the complexity of (5) is low, the computational cost of calculating the energy function defined in (4) is significantly lower than the one used in [1]. -
(ii)
In the approach reported in [19, 21, 22], the potential function is defined as
 (10)
(10)which neither takes into account the variation of features across homogeneous regions nor allows flexible weighting according to the discriminatory power of the local features. In this work, the value of potential
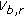 is not bipolar, but linearly dependent on the difference between
is not bipolar, but linearly dependent on the difference between 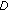 and
and 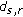 . This characteristic gives blocks of different voting weight. A block
. This characteristic gives blocks of different voting weight. A block  with a feature disparity
with a feature disparity  closer to the threshold
closer to the threshold 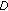 is less discriminative and therefore should have less say in determining its neighbours' classes.
is less discriminative and therefore should have less say in determining its neighbours' classes. -
(iii)
Assuming the texture features employed are adequately discriminative, then
-
(a)
the first case of (7) indicates that if the same class label
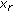 is to be assigned to site
is to be assigned to site  , then,
, then, -
(1)
if block
 and
and  do belong to the same class (i.e.,
do belong to the same class (i.e., 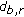 is significantly smaller than
is significantly smaller than  ), a small value,
), a small value, 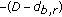 , for potential
, for potential  is given. This is reasonable because this is a correct labelling and should be encouraged with a lower cost,
is given. This is reasonable because this is a correct labelling and should be encouraged with a lower cost, -
(2)
if block
 and
and  do not belong to the same class (i.e.,
do not belong to the same class (i.e., 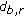 is significantly greater than
is significantly greater than 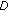 ), a large value,
), a large value, 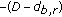 , for potential
, for potential 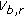 will be given as a penalty to discourage this incorrect labelling;
will be given as a penalty to discourage this incorrect labelling;
-
(1)
-
(b)
the second case of (5) indicates that if a class label different from
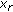 is to be assigned to site
is to be assigned to site 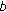 , then,
, then, -
(1)
if block
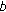 and
and  do belong to the same class, a large value,
do belong to the same class, a large value, 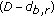 , for potential
, for potential 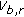 is given to penalise this incorrect labelling,
is given to penalise this incorrect labelling, -
(2)
if block
 and
and  do not belong to the same class, a small value,
do not belong to the same class, a small value,  , for potential
, for potential 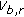 will be given to encourage this correct labelling.
will be given to encourage this correct labelling.
-
(1)
-
(a)
In optimization problems, deterministic relaxation [22] and stochastic relaxation [1, 21] are two common techniques for selecting next states based on the objective function associated with the current states and the observed data. In the context of this work, given the energy function (the objective function), a site  can be assigned a class label in a deterministic sense according to (11)
can be assigned a class label in a deterministic sense according to (11)

where  is defined in (4).
is defined in (4).
Although deterministic relaxation is relatively less computationally intensive compared to stochastic relaxation, a main limitation is that the relaxation process may get trapped in local optimal states more easily. Therefore, in this work we choose stochastic relaxation, which combines simulated annealing (SA) [1, 21] with the MRF model of (4), to select an optimal label from the ones associated with the members of the voting pool for site  . With this stochastic sense, a modified model of (4) is defined as
. With this stochastic sense, a modified model of (4) is defined as

where  in (12) is the pseudotemperature (also called annealing schedule) in iteration
in (12) is the pseudotemperature (also called annealing schedule) in iteration  at resolution level
at resolution level 

where  in (13) is a constant which determines the initial temperature and the convergence rate. The higher the value of
in (13) is a constant which determines the initial temperature and the convergence rate. The higher the value of  is, the higher the starting pseudotemperature is and the less likely the labelling process will get trapped at local minima, but the slower the convergence rate is. Because the labelling at low resolution levels is conditioned on the segmentation result of the higher resolution levels, wherein the number of blocks is smaller,
is, the higher the starting pseudotemperature is and the less likely the labelling process will get trapped at local minima, but the slower the convergence rate is. Because the labelling at low resolution levels is conditioned on the segmentation result of the higher resolution levels, wherein the number of blocks is smaller,  is varied with
is varied with  , with greater values at low
, with greater values at low  (high resolution level). Usually, the value of
(high resolution level). Usually, the value of  has to be chosen empirically according to the range of the energy function. Note that in the special case when
has to be chosen empirically according to the range of the energy function. Note that in the special case when  is fixed at 0 regardless
is fixed at 0 regardless  and
and  , the stochastic model of (12) is equivalent to the deterministic model as expressed in (11).
, the stochastic model of (12) is equivalent to the deterministic model as expressed in (11).
The search for the optimal label  is the process of maximizing thea posteriori probability of (12). In the context of simulated annealing and stochastic relaxation, the label of each voting member has a chance of being chosen proportional to its probability calculated according to (12).
is the process of maximizing thea posteriori probability of (12). In the context of simulated annealing and stochastic relaxation, the label of each voting member has a chance of being chosen proportional to its probability calculated according to (12).
The algorithm can certainly involve only one or more than two random sites. There is no theoretical backing for determining the number of random sites as this is application dependent. For example, when segmenting images with disjoint small regions of the same texture, the inclusion of more random sites increases the chances for the disjoint small regions to establish contact. However, this is achieved at the expense of computation complexity because there will be more sites and more labels to deal with. On the other hand, when segmenting images without disjoint small regions of the same class, the inclusion of less random sites is more desirable. Nonetheless, the word "small" in this context is not well defined, and maybe there is no way of defining it. Moreover, this question about how many random sites are enough is also directly related to the setting of the starting temperature for simulated annealing. With the number of random sites fixed, when the starting temperature is set high, the algorithm will iterate longer, allowing more sites to be interacted with. So, like the starting temperature, the number of random sites has to be determined in an ad hoc manner. In this work, given the small number of the standing members (i.e., 4 first-order neighbours), including half as many random sites is a reasonable guess.
As stated in Step (4.2), upon convergence, the algorithm propagates the segmentation result of the current level down to the next level for refinement. The propagated result is the class label configuration, which will be used as the initial configuration at the new level.
4. Experiments and Performance Analyses
To test the algorithm's computational efficiency and ability to alleviate the oversegmentation problem and to assign the same label to the disjoint regions of the same texture by using the voting pool, the noisy image of  pixels in Figure 3 is used. This figure contains two disjoint darker regions with a mean equal to 80 and a variance equal to 100 separated by another brighter region with a mean equal to 100 and a variance equal to 100. The point of using the image in Figure 3 is that the two types of "texture" regions, separated by straight boundaries, are homogeneous so that even the variation of the features extracted from small blocks of the same region is small. This means that the performance we want to evaluate is not biased by the features. We apply the proposed algorithm and the previous one reported in [1] 100 times each to segment the image. To compare the performance on equal basis, we allow both algorithms to use the same energy function defined in (6). Table 1 differently shows the two algorithms' performance in terms of computational cost measured by average iterations, oversegmentation rate, and rate of labelling disjoint regions of the same texture when the image in Figure 3 is divided into 64 blocks. Table 2 lists the same measurements of the two algorithms' performance when the same image is divided into 256 blocks. The average iterations in Table 1 indicate that the proposed algorithm is significantly more efficient in terms of computational cost than the previous algorithm even without taking the other two metrics of performance into account. They also indicate that the proposed algorithm's computational cost increases significantly more slowly than that of the previous algorithm. Moreover, we can see that at
pixels in Figure 3 is used. This figure contains two disjoint darker regions with a mean equal to 80 and a variance equal to 100 separated by another brighter region with a mean equal to 100 and a variance equal to 100. The point of using the image in Figure 3 is that the two types of "texture" regions, separated by straight boundaries, are homogeneous so that even the variation of the features extracted from small blocks of the same region is small. This means that the performance we want to evaluate is not biased by the features. We apply the proposed algorithm and the previous one reported in [1] 100 times each to segment the image. To compare the performance on equal basis, we allow both algorithms to use the same energy function defined in (6). Table 1 differently shows the two algorithms' performance in terms of computational cost measured by average iterations, oversegmentation rate, and rate of labelling disjoint regions of the same texture when the image in Figure 3 is divided into 64 blocks. Table 2 lists the same measurements of the two algorithms' performance when the same image is divided into 256 blocks. The average iterations in Table 1 indicate that the proposed algorithm is significantly more efficient in terms of computational cost than the previous algorithm even without taking the other two metrics of performance into account. They also indicate that the proposed algorithm's computational cost increases significantly more slowly than that of the previous algorithm. Moreover, we can see that at  , only 1% of the applications of the proposed algorithm result in oversegmentation and labelling of the two dark regions differently, due to the low initial annealing temperature, while no oversegmentation and mislabelling of the dark regions occur when
, only 1% of the applications of the proposed algorithm result in oversegmentation and labelling of the two dark regions differently, due to the low initial annealing temperature, while no oversegmentation and mislabelling of the dark regions occur when  is only 50, with an average computational cost of only 6.2 iterations. On the contrary, the previous algorithm could only yield no oversegmentation when
is only 50, with an average computational cost of only 6.2 iterations. On the contrary, the previous algorithm could only yield no oversegmentation when  , with the average computational cost as high as 131.3 iterations. The rates of labelling the two dark regions inconsistently associated with the proposed and previous algorithms also reveal another superior aspect of the proposed algorithm. As we mentioned earlier, the larger the textured regions are, the higher the probability that the previous algorithm will encounter the problem of oversegmentation.
, with the average computational cost as high as 131.3 iterations. The rates of labelling the two dark regions inconsistently associated with the proposed and previous algorithms also reveal another superior aspect of the proposed algorithm. As we mentioned earlier, the larger the textured regions are, the higher the probability that the previous algorithm will encounter the problem of oversegmentation.
 when the image in Figure 3 is divided into 64 blocks.
when the image in Figure 3 is divided into 64 blocks. when the image in Figure 3 is divided into 256 blocks.
when the image in Figure 3 is divided into 256 blocks.We apply the two algorithms to the same image when it is divided into 256 blocks and list the results in Table 2. With 4 times more blocks, the proposed algorithm demonstrates the same level of performance, in terms of oversegmentation rate and rate of labelling the two dark regions differently, with a slight increase of computational cost compared to Table 1. For the previous algorithm, the computational cost increases more significantly (with an average computational cost of 282.6 iterations) and the initial temperature has to be set to 600 in order to avoid oversegmentation. On the other hand, the proposed algorithm is able to achieve this level of performance with  and an average cost of 10.1 iterations. Nevertheless, in all cases, as demonstrated in Table 2, the previous algorithm completely fails to label the two dark regions consistently. These two experiments demonstrate that the voting pool adopted in the proposed algorithm can effectively and efficiently facilitate both local and global interactions among the blocks to avoid the key limitations of the previous algorithm.
and an average cost of 10.1 iterations. Nevertheless, in all cases, as demonstrated in Table 2, the previous algorithm completely fails to label the two dark regions consistently. These two experiments demonstrate that the voting pool adopted in the proposed algorithm can effectively and efficiently facilitate both local and global interactions among the blocks to avoid the key limitations of the previous algorithm.
Figures 4, 5, and 6 illustrate the segmentation results of three textured images, Image I, II, and III, at different resolution levels. This time the previous algorithm uses the energy function defined in [1] while the proposed algorithm uses the one adopted in this work. The value of  in (13) is set to 300 at the nominal top resolution level and reduced by 50 after proceeding to the next resolution level. The results are shown in (a) to (d) of Figures 4 to 6, respectively. The results show the increase in segmentation accuracy and the algorithm's ability to alleviate the class-boundary uncertainty as the algorithm descends the multiresolution structure. The comparisons of performance in terms of segmentation error rate (%) and computational cost measured by iterations per pixel(# i/p) are listed in Tables 3 to 5, respectively. Note that the total computational cost has to be measured by adding up the costs incurred at all resolution levels. Because the block sizes at various resolution level are not the same, instead of using iterations, a more suitable metric would be iterations per pixel(# i/p), which is equal to 4 × iterations/block size. Note also that the "4" in the expression is to reflect the fact that, due the sampling windows' 50% overlap, each block is only associated with a quarter of the area in the centre of the block. For both algorithms in all the three cases, the segmentation error rates at the bottom resolution level are quite close. However, the significant performance gap in terms of computational cost (# i/p) again reveals the merit of the proposed MRF algorithm. According to [1], the previous algorithm came with a boundary process. Although the boundary process made the boundaries look smoother, it did not provide significant improvement in terms of segmentation accuracy. Therefore, we do not include the boundary process in this work. Note, in all the experiments, no a priori knowledge about the number and types of textures contained in the images in question is provided to the algorithm. Yet, the algorithm is able to segment the images correctly. These results indicate that the proposed algorithm requires no supervision by the user.
in (13) is set to 300 at the nominal top resolution level and reduced by 50 after proceeding to the next resolution level. The results are shown in (a) to (d) of Figures 4 to 6, respectively. The results show the increase in segmentation accuracy and the algorithm's ability to alleviate the class-boundary uncertainty as the algorithm descends the multiresolution structure. The comparisons of performance in terms of segmentation error rate (%) and computational cost measured by iterations per pixel(# i/p) are listed in Tables 3 to 5, respectively. Note that the total computational cost has to be measured by adding up the costs incurred at all resolution levels. Because the block sizes at various resolution level are not the same, instead of using iterations, a more suitable metric would be iterations per pixel(# i/p), which is equal to 4 × iterations/block size. Note also that the "4" in the expression is to reflect the fact that, due the sampling windows' 50% overlap, each block is only associated with a quarter of the area in the centre of the block. For both algorithms in all the three cases, the segmentation error rates at the bottom resolution level are quite close. However, the significant performance gap in terms of computational cost (# i/p) again reveals the merit of the proposed MRF algorithm. According to [1], the previous algorithm came with a boundary process. Although the boundary process made the boundaries look smoother, it did not provide significant improvement in terms of segmentation accuracy. Therefore, we do not include the boundary process in this work. Note, in all the experiments, no a priori knowledge about the number and types of textures contained in the images in question is provided to the algorithm. Yet, the algorithm is able to segment the images correctly. These results indicate that the proposed algorithm requires no supervision by the user.
It is also worth noting that, in Figure 4, the elements/textons of the recursive texture pattern are greater than 16 pixels in at least one dimension, which is greater than the block dimension at the resolution level 5. Yet the proposed algorithm is capable of detecting the boundaries accurately even at the bottom level, where the block size is only  pixels. This is due to the use of multiresolution approach: we divide the images into large blocks at the top level to collect reliable features (at the expense of boundary certainty) and use the coarse segmentation result to condition the segmentation at lower level.
pixels. This is due to the use of multiresolution approach: we divide the images into large blocks at the top level to collect reliable features (at the expense of boundary certainty) and use the coarse segmentation result to condition the segmentation at lower level.
We have also applied the algorithm to natural colour images (Orchid) as shown in Figure 7(a). Because the characteristics of this image are different from those in Figures 4 to 6, the features used to describe each block are the mean values of R, G, and B components. The size of the image is  pixels. We start the program at resolution level 3 (i.e.,
pixels. We start the program at resolution level 3 (i.e.,  , but only demonstrate the segmentation results at level 4 to 6 in Figures 7(b)–7(d), respectively. This experiment conforms to what we mentioned in Section 3 that the proposed segmentation algorithm can be incorporated with any discriminative features. The key challenges posed by this image are the following. (1) The feature difference between the leaves and the background is insignificant when compared to the difference between the flower and either the leaves or the background. We divide Figure 7(a) into 2400 blocks of
, but only demonstrate the segmentation results at level 4 to 6 in Figures 7(b)–7(d), respectively. This experiment conforms to what we mentioned in Section 3 that the proposed segmentation algorithm can be incorporated with any discriminative features. The key challenges posed by this image are the following. (1) The feature difference between the leaves and the background is insignificant when compared to the difference between the flower and either the leaves or the background. We divide Figure 7(a) into 2400 blocks of  pixels and display the colour (feature) distribution of those blocks in the (R, G, B) space as demonstrated in Figure 8. We can see that an ineffective segmentation algorithm could classify the blocks belonging to the leaves and background into the same group. (2) The left part of the flower shape is quite rugged. (3) There are two narrow orange "peninsulas", one pointing upwards and the other downwards. It can be seen from Figure 7(b) that, because of class-boundary uncertainty, many spurious small regions form along the boundaries between real regions, the rugged boundaries and the two peninsulas in particular. The sizes of the small regions can be reduced at finer resolution levels, but the number of even smaller regions will also increase at finer resolution levels. These small regions are inherent to the class-boundary uncertainty. Their areas are less significant at finer resolution levels, and segmentation inaccuracy at higher resolution levels can be reduced at finer levels; therefore, it is computationally undesirable to repeat the same algorithm at finer levels with the same sophistication. To keep computational cost low without sacrificing segmentation accuracy, at the two finest resolution levels, we apply the algorithm with stochastic relaxation (12) to all the blocks for three iterations and then only to blocks with at least one 4-neighbour system carrying a different class label (i.e., the blocks along the boundaries) in a deterministic relaxation manner (11).
pixels and display the colour (feature) distribution of those blocks in the (R, G, B) space as demonstrated in Figure 8. We can see that an ineffective segmentation algorithm could classify the blocks belonging to the leaves and background into the same group. (2) The left part of the flower shape is quite rugged. (3) There are two narrow orange "peninsulas", one pointing upwards and the other downwards. It can be seen from Figure 7(b) that, because of class-boundary uncertainty, many spurious small regions form along the boundaries between real regions, the rugged boundaries and the two peninsulas in particular. The sizes of the small regions can be reduced at finer resolution levels, but the number of even smaller regions will also increase at finer resolution levels. These small regions are inherent to the class-boundary uncertainty. Their areas are less significant at finer resolution levels, and segmentation inaccuracy at higher resolution levels can be reduced at finer levels; therefore, it is computationally undesirable to repeat the same algorithm at finer levels with the same sophistication. To keep computational cost low without sacrificing segmentation accuracy, at the two finest resolution levels, we apply the algorithm with stochastic relaxation (12) to all the blocks for three iterations and then only to blocks with at least one 4-neighbour system carrying a different class label (i.e., the blocks along the boundaries) in a deterministic relaxation manner (11).
5. Conclusions
In this work, we have addressed the need for tackling the class boundary uncertainty issue in the context of texture segmentation and the importance of facilitating long-range interaction among image blocks/sites in order to avoid oversegmentation and mislabelling of disjoint regions with the same texture. In response to these, we have proposed an unsupervised multiresolution conditional random field approach, which utilises a voting pool consisting of local neighbours and distant sites. The proposed algorithm is capable of not only alleviating the problems of oversegmentation and mislabelling disjoint regions with the same texture, but also carrying out the segmentation without a priori knowledge about the number and types of textures contained in the input image. Moreover, with sufficient information gathered through the incorporation of long-range interactions, the convergence rate of the proposed algorithm is faster. To the author's knowledge, no previous attempt has been made to include long-range block in the neighbourhood of MRF models.
References
Wilson R, Li C-T: A class of discrete multiresolution random fields and its application to image segmentation. IEEE Transactions on Pattern Analysis and Machine Intelligence 2003, 25(1):42-56. 10.1109/TPAMI.2003.1159945
Aldasoro CCR, Bhalerao A: Volumetric texture segmentation by discriminant feature selection and multiresolution classification. IEEE Transactions on Medical Imaging 2007, 26(1):1-14.
Athanasiadis EI, Cavouras DA, Glotsos DT, Georgiadis PV, Kalatzis IK, Nikiforidis GC: Segmentation of complementary DNA microarray images by wavelet-based markov random field model. IEEE Transactions on Information Technology in Biomedicine 2009, 13(6):1068-1074.
Liu X, Langer DL, Haider MA, Yang Y, Wernick MN, Yetik IS: Prostate cancer segmentation with simultaneous estimation of Markov random field parameters and class. IEEE Transactions on Medical Imaging 2009, 28(6):906-915.
Beaulieu J-M, Touzi R: Segmentation of textured polarimetric SAR scenes by likelihood approximation. IEEE Transactions on Geoscience and Remote Sensing 2004, 42(10):2063-2072.
Deng H, Clausi DA: Unsupervised segmentation of synthetic aperture radar sea ice imagery using a novel Markov random field model. IEEE Transactions on Geoscience and Remote Sensing 2005, 43(3):528-537.
Fjørtoft R, Delignon Y, Pieczynski W, Sigelle M, Tupin F: Unsupervised classification of radar images using hidden Markov chains and hidden Markov random fields. IEEE Transactions on Geoscience and Remote Sensing 2003, 41(3):675-686. 10.1109/TGRS.2003.809940
De Grandi GD, Lee J-S, Schuler DL: Target detection and texture segmentation in polarimetric SAR images using a wavelet frame: theoretical aspects. IEEE Transactions on Geoscience and Remote Sensing 2007, 45(11):3437-3453.
Hazel GG: Multivariate gaussian MRP for multispectral scene segmentation and anomaly detection. IEEE Transactions on Geoscience and Remote Sensing 2000, 38(3):1199-1211. 10.1109/36.843012
Deng Y, Manjunath BS: Unsupervised segmentation of color-texture regions in images and video. IEEE Transactions on Pattern Analysis and Machine Intelligence 2001, 23(8):800-810. 10.1109/34.946985
Epifanio I, Soille P: Morphological texture features for unsupervised and supervised segmentations of natural landscapes. IEEE Transactions on Geoscience and Remote Sensing 2007, 45(4):1074-1083.
Huang J, Liu Z, Wang Y: Joint scene classification and segmentation based on Hidden Markov Model. IEEE Transactions on Multimedia 2005, 7(3):538-550.
Mignotte M, Collet C, Pérez P, Bouthemy P: Sonar image segmentation using an unsupervised hierarchical MRF model. IEEE Transactions on Image Processing 2000, 9(7):1216-1231. 10.1109/83.847834
Gevers T: Image segmentation and similarity of color-texture objects. IEEE Transactions on Multimedia 2002, 4(4):509-516. 10.1109/TMM.2002.802023
Sarkar A, Biswas MK, Kartikeyan B, Kumar V, Majumder KL, Pal DK: A MRF model-based segmentation approach to classification for multispectral imagery. IEEE Transactions on Geoscience and Remote Sensing 2002, 40(5):1102-1113. 10.1109/TGRS.2002.1010897
Wang Z, Boesch R: Color- and texture-based image segmentation for improved forest delineation. IEEE Transactions on Geoscience and Remote Sensing 2007, 45(10):3055-3062.
Zhong P, Wang R: A multiple conditional random fields ensemble model for urban area detection in remote sensing optical images. IEEE Transactions on Geoscience and Remote Sensing 2007, 45(12):3978-3988.
Hill PR, Nishan Canagarajah C, Bull DR: Image segmentation using a texture gradient based watershed transform. IEEE Transactions on Image Processing 2003, 12(12):1618-1633. 10.1109/TIP.2003.819311
Chatzis SP, Varvarigou TA: A fuzzy clustering approach toward Hidden Markov random field models for enhanced spatially constrained image segmentation. IEEE Transactions on Fuzzy Systems 2008, 16(5):1351-1361.
Liang K-H, Tjahjadi T: Adaptive scale fixing for multiscale texture segmentation. IEEE Transactions on Image Processing 2006, 15(1):249-256.
Geman S, Geman D: STOCHASTIC RELAXATION, GIBBS DISTRIBUTIONS, AND THE BAYESIAN RESTORATION OF IMAGES. IEEE Transactions on Pattern Analysis and Machine Intelligence 1984, 6(6):721-741.
Noda H, Shirazi MN, Kawaguchi E: MRF-based texture segmentation using wavelet decomposed images. Pattern Recognition 2002, 35(4):771-782. 10.1016/S0031-3203(01)00077-2
Rezaee MR, Van Der Zwet PMJ, Lelieveldt BPF, van der Geest RJ, Reiber JHC: A multiresolution image segmentation technique based on pyramidal segmentation and fuzzy clustering. IEEE Transactions on Image Processing 2000, 9(7):1238-1248. 10.1109/83.847836
Sagiv C, Sochen NA, Zeevi YY: Integrated active contours for texture segmentation. IEEE Transactions on Image Processing 2006, 15(6):1633-1646.
Jenssen R, Eltoft T: Independent component analysis for texture segmentation. Pattern Recognition 2003, 36(10):2301-2315. 10.1016/S0031-3203(03)00131-6
Xia Y, Feng D, Zhao R: Morphology-based multifractal estimation for texture segmentation. IEEE Transactions on Image Processing 2006, 15(3):614-623.
Melas DE, Wilson SP: Double Markov random fields and Bayesian image segmentation. IEEE Transactions on Signal Processing 2002, 50(2):357-365. 10.1109/78.978390
Wu J, Chung ACS: A segmentation model using compound Markov random fields based on a boundary model. IEEE Transactions on Image Processing 2007, 16(1):241-252.
Besag J: Spatial interaction and the statistical analysis of lattice systems. Journal of the Royal Statistical Society (Serial B) 1964, 36: 192-236.
Li C-T: Approach to reducing the labeling cost of Markov random fields within an infinite label space. Signal Processing 2001, 81(3):609-620. 10.1016/S0165-1684(00)00235-8
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, CT. A Conditional Random Field Approach to Unsupervised Texture Image Segmentation. EURASIP J. Adv. Signal Process. 2010, 167942 (2010). https://doi.org/10.1155/2010/167942
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/167942


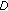 ,
, 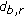 ,
, 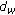 , and
, and 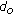 are all adaptive to the content of the image. Since the complexity of (5) is low, the computational cost of calculating the energy function defined in (4) is significantly lower than the one used in [
are all adaptive to the content of the image. Since the complexity of (5) is low, the computational cost of calculating the energy function defined in (4) is significantly lower than the one used in [
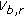 is not bipolar, but linearly dependent on the difference between
is not bipolar, but linearly dependent on the difference between 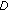 and
and 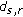 . This characteristic gives blocks of different voting weight. A block
. This characteristic gives blocks of different voting weight. A block  with a feature disparity
with a feature disparity  closer to the threshold
closer to the threshold 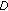 is less discriminative and therefore should have less say in determining its neighbours' classes.
is less discriminative and therefore should have less say in determining its neighbours' classes.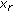 is to be assigned to site
is to be assigned to site  , then,
, then,  and
and  do belong to the same class (i.e.,
do belong to the same class (i.e., 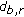 is significantly smaller than
is significantly smaller than  ), a small value,
), a small value, 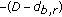 , for potential
, for potential  is given. This is reasonable because this is a correct labelling and should be encouraged with a lower cost,
is given. This is reasonable because this is a correct labelling and should be encouraged with a lower cost, and
and  do not belong to the same class (i.e.,
do not belong to the same class (i.e., 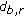 is significantly greater than
is significantly greater than 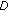 ), a large value,
), a large value, 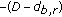 , for potential
, for potential 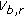 will be given as a penalty to discourage this incorrect labelling;
will be given as a penalty to discourage this incorrect labelling;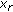 is to be assigned to site
is to be assigned to site 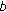 , then,
, then, 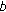 and
and  do belong to the same class, a large value,
do belong to the same class, a large value, 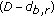 , for potential
, for potential 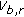 is given to penalise this incorrect labelling,
is given to penalise this incorrect labelling, and
and  do not belong to the same class, a small value,
do not belong to the same class, a small value,  , for potential
, for potential 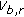 will be given to encourage this correct labelling.
will be given to encourage this correct labelling.





 pixels taken from Figure
pixels taken from Figure