- Research Article
- Open access
- Published:
SQNR Estimation of Fixed-Point DSP Algorithms
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 171027 (2010)
Abstract
A fast and accurate quantization noise estimator aiming at fixed-point implementations of Digital Signal Processing (DSP) algorithms is presented. The estimator enables significant reduction in the computation time required to perform complex word-length optimizations. The proposed estimator is based on the use of Affine Arithmetic (AA) and it is presented in two versions: (i) a general version suitable for differentiable nonlinear algorithms, and Linear Time-Invariant (LTI) algorithms with and without feedbacks; and (ii) an LTI optimized version. The process relies on the parameterization of the statistical properties of the noise at the output of fixed-point algorithms. Once the output noise is parameterized (i.e., related to the fixed-point formats of the algorithm signals), a fast estimation can be applied throughout the word-length optimization process using as a precision metric the Signal-to-Quantization Noise Ratio (SQNR). The estimator is tested using different LTI filters and transforms, as well as a subset of non-linear operations, such as vector operations, adaptive filters, and a channel equalizer. Fixed-point optimization times are boosted by three orders of magnitude while keeping the average estimation error down to 4%.
1. Introduction
The original infinite precision of an algorithm based on the use of real arithmetic must be reduced to the practical precision bounds imposed by digital computing systems. Word-length optimization (WLO) aims at the selection of the variables' word-lengths of an algorithm to comply with a certain output noise constraint while optimizing the characteristics of the implementation (e.g., area, speed or power consumption). Normally, the precision loss committed is computed by using a double precision floating-point arithmetic description of the algorithm as a reference and, although there are some works on quantization for custom floating-point arithmetic [1–3], the common approach is to implement the system using fixed-point (FxP) arithmetic, since this leads to lower cost implementations in terms of area, speed, and power consumption [4–7].
WLO is a slow process due to the fact that the optimization is very complex (NP-hard [8]) and also because of the necessity of a continuous assessment of the algorithm accuracy which may involve a high computational load. This estimation is normally performed adopting a simulation-based approach [7, 9, 10] which leads to exceedingly long design times. However, in the last few years, there have been attempts to provide fast estimation methods based on analytical techniques. These approaches can be applied to Linear Time-Invariant (LTI) systems [6, 11] and to differentiable nonlinear systems [12–15]. As for the noise metric used, they are based on the peak value [15] and on the computation of SQNR [6, 11–14]. Since SQNR is a very popular error metric within DSP systems, our work aims at fast SQNR estimation techniques for LTI and differentiable nonlinear systems.
This paper contains the following contributions:
-
(i)
a novel Affine-Arithmetic (AA) SQNR estimator optimized for LTI algorithms,
-
(ii)
a novel AA-based SQNR estimator for LTI and differentiable algorithms. Previous approaches were not able to deal with feedback systems, or produced overestimations.
Our approach enables addressing complex WLO techniques, since the computation times are drastically reduced while providing high levels of accuracy.
The paper is structured as follows. In Section 2, related work is discussed. Section 3 deals with fixed-point optimization. Section 4 presents the grounds of the novel SQNR estimation proposal. In Section 5, the benchmarks used for validation are described. Performance results are collected in Section 6. And finally, Section 7 draws the conclusions.
2. Related Work
In this section, we focus on those approaches aiming at estimating the quantization noise to avoid the execution of time-consuming simulations [7, 9, 18] and, therefore, that support fast WLO. We disregard those that are not fully automated [19–22], but consider those that, even though are not implemented within an automatic WLO engine, could be easily integrated within one. Also, we do not consider in this analysis approaches that focus on error-free implementations [23–25].
The Signal-to-Quantization Noise Ratio (SQNR) is a popular quality metric in DSP systems. However, only recently it has been considered in the development of fast quantization noise estimators. Approaches such as [19–25] and also the fully automated [15, 26–28] aim basically at peak-value estimates. Most of these works are based on the use of (i) interval arithmetic (IA) [29], which produces significant overestimations in general, and intolerable overestimations in the presence of loops; (ii) multi-interval arithmetic (MIA) [30], which improves the results of IA but it still performs poorly in the presence of loops; (iii) affine arithmetic [31], which solves the cancellation problem of IA, and can alleviate overestimation by applying confidence intervals; and (iv) the computation of first-order derivatives [15, 28], mostly combined with a worst-case analysis, that leads again to overestimation. Due to its interest for DSP applications, only approaches that consider SQNR as a quality metric are fully analyzed in this section.
Table 1 contains information about the main approaches regarding quantization noise fast estimation under the mentioned premises. The first column holds the reference to the approach. The second column indicates if LTI or nonlinear (NL) algorithms are supported. Column 3 shows if the algorithms are cyclic (i.e., containing loops) or not. The computational complexity of the noise parameterization stage, if applicable, is shown in the fourth column. Also, the computational complexity of the noise estimation itself is presented in column 5. The last two columns contain information about the accuracy of the estimates and comments highlighting interesting features or drawbacks of the approaches.
The approaches in the table have been grouped according to the type of algorithm being addressed. The first three rows correspond to approaches aimed at LTI algorithms, the next three rows to those addressing nonlinear algorithms (also valid for LTI systems), and the last two rows describe the features of the two approaches proposed in this paper.
2.1. Linear Time-Invariant Algorithms
Let us start with LTI-oriented methods. Given an algorithm with  signals where each signal is quantized to
signals where each signal is quantized to  bits, it is possible to relate the number of bits to the power of the noise at the output of the algorithm in steady state by means of the following expression:
bits, it is possible to relate the number of bits to the power of the noise at the output of the algorithm in steady state by means of the following expression:

where  is the transfer function from signal
is the transfer function from signal  to output
to output  , and
, and  and
and  are the variance and mean of the quantization noise associated to signal
are the variance and mean of the quantization noise associated to signal  —which is related to
—which is related to  . This expression can be rewritten more compactly using vectors
. This expression can be rewritten more compactly using vectors  ,
,  ,
,  , and
, and  as,
as,





Note that  and
and  can be computed by means of a graph analysis, and once they are determined, the output noise power can be estimated from
can be computed by means of a graph analysis, and once they are determined, the output noise power can be estimated from  and
and  .
.
In [6] a two-step method is applied where, first, vectors  and
and  are computed, and then, expression (2) is used to estimate the output noise variance during WLO. The Parseval Theorem [32] is applied in order to compute expression (5), since it is possible to obtain an equivalent expression that makes use of the impulse response from signal
are computed, and then, expression (2) is used to estimate the output noise variance during WLO. The Parseval Theorem [32] is applied in order to compute expression (5), since it is possible to obtain an equivalent expression that makes use of the impulse response from signal  to the output of the systems (
to the output of the systems ( ), instead of using
), instead of using  . This highly simplifies the computational cost. If the length of the input vectors is long enough, expression (1) can be estimated with high precision leading to highly accurate quantization noise estimations.
. This highly simplifies the computational cost. If the length of the input vectors is long enough, expression (1) can be estimated with high precision leading to highly accurate quantization noise estimations.
An AA-based approach is presented in [11]. The approach is based again on the computation of  for each signal. Due to the characteristics of AA, it is possible to compute all
for each signal. Due to the characteristics of AA, it is possible to compute all  simultaneously. The process has not been divided into parameterization (extraction of vectors
simultaneously. The process has not been divided into parameterization (extraction of vectors  and
and  ) and noise estimation. Instead, everything is computed at once. It can be seen in Table 1 that the computational cost is similar to the total cost of [6] (e.g., parameterization plus estimation times). Also, the quality of the estimates is high, since they are based on (1). This approach is further developed in Section 4.3 in order convert it into a two-step method, thus, allowing faster noise estimation (see Table 1, this work—LTI).
) and noise estimation. Instead, everything is computed at once. It can be seen in Table 1 that the computational cost is similar to the total cost of [6] (e.g., parameterization plus estimation times). Also, the quality of the estimates is high, since they are based on (1). This approach is further developed in Section 4.3 in order convert it into a two-step method, thus, allowing faster noise estimation (see Table 1, this work—LTI).
The approach in [16] also relies on (1) to present a two-step estimation method. The parameterization is based on the application of graph transforms that allow to obtain the vectors  and
and  (5) and (6). As it can be seen in Table 1, the performance in terms of computation time and accuracy is equivalent to the other two approaches.
(5) and (6). As it can be seen in Table 1, the performance in terms of computation time and accuracy is equivalent to the other two approaches.
2.2. NonLinear Systems
The approaches aimed at nonlinear systems are mainly based on perturbation theory, where the effect of the quantization of each algorithm's signal on the quality of the output signal is supposed to be small. This allows to apply first-order Taylor expansion to each nonlinear operation in order to characterize the effect of the quantization of the inputs of the operations. This constrains the application to algorithms composed of differentiable operations. The existent methods enable us to obtain an expression similar to (2) that relates the word-lengths of signals to the power—also mean and variance—of the quantization noise at the output. This will be further explained in Section 4.2 (19).
In [12] a hybrid method which combines simulations and analytical techniques to estimate the variance of the noise is proposed. The estimator is suitable for nonrecursive and recursive algorithms. The parameterization phase is relatively fast, since it requires  simulations for an algorithm with
simulations for an algorithm with  variables. The noise model is based on [33] and second order effects are neglected by applying first order Taylor expansions. However, the paper seems to suggest that the contributions of the signal quantization noises at the output can be added, assuming that the noises are independent. In nonlinear systems, this is a strong assumption that leads to variance underestimation. The accuracy of the method is not supported with any empirical data.
variables. The noise model is based on [33] and second order effects are neglected by applying first order Taylor expansions. However, the paper seems to suggest that the contributions of the signal quantization noises at the output can be added, assuming that the noises are independent. In nonlinear systems, this is a strong assumption that leads to variance underestimation. The accuracy of the method is not supported with any empirical data.
In [14] another method suitable for nonrecursive and recursive algorithms is presented. Here,  simulations as well as a curve fitting technique (with
simulations as well as a curve fitting technique (with  variables) are required to parameterize quantization noise. On the one hand, the noise produced by each signal is modeled following the traditional quantization noise model from [34, 35], which is less accurate than [33], and, again, second order statistics are neglected. On the other hand, the expression of the estimated noise power accounts for noise interdependencies, which is a better approach than [12]. The method is tested with an LMS adaptive filter and the accuracy is evaluated graphically. There is no information about computation times.
variables) are required to parameterize quantization noise. On the one hand, the noise produced by each signal is modeled following the traditional quantization noise model from [34, 35], which is less accurate than [33], and, again, second order statistics are neglected. On the other hand, the expression of the estimated noise power accounts for noise interdependencies, which is a better approach than [12]. The method is tested with an LMS adaptive filter and the accuracy is evaluated graphically. There is no information about computation times.
Finally, in [13] the parameterization is performed by means of  simulations and the estimator is suitable only for nonrecursive systems. The accuracy of this approach seems to be the highest since it uses the model from [33] and it accounts for noise interdependencies. Although, the information provided about accuracy is more complete, it is still not sufficient, since the estimator is tested in only a few SQNR scenarios.
simulations and the estimator is suitable only for nonrecursive systems. The accuracy of this approach seems to be the highest since it uses the model from [33] and it accounts for noise interdependencies. Although, the information provided about accuracy is more complete, it is still not sufficient, since the estimator is tested in only a few SQNR scenarios.
2.3. This Work
As aforementioned, we present two approaches: one exclusive for LTI algorithms in steady state, and the other for differentiable algorithms which are a subset of nonlinear algorithms. The LTI-oriented approach is based on [11] and it basically enables the division of the estimation process into two steps. One step is devoted to parameterization, while the other is dedicated to perform fast estimations. This method is equivalent to the other methods present in the literature. The advantage that it offers is that now it is possible to analyze the most important finite word-length effects (SQNR analysis, peak value analysis, dynamic range, limit cycles) using the very same AA simulation engine.
Regarding nonlinear systems, our approach tries to overcome most of the drawbacks of the works presented above. It deals with nonrecursive and recursive systems, using the accurate noise model from [33] and also accounting for noise interdependencies. The parameterization time can be quite long for algorithms that contain loops. However, as we will see in Section 6, the computation times are within standard times, and the benefits of fast estimations make up for the sometimes slow parameterization process.
3. Word-Length Optimization
The starting point of WLO is a signal flow graph  that contains information about the signal FxP formats and the data dependencies. The FxP formats of signals enable the computation of the statistical parameters of the quantization noises introduced by them, and the data dependencies are essential to obtain a noise model that relates the signals' noise parameters with the overall noise at the output of the algorithm. Set
that contains information about the signal FxP formats and the data dependencies. The FxP formats of signals enable the computation of the statistical parameters of the quantization noises introduced by them, and the data dependencies are essential to obtain a noise model that relates the signals' noise parameters with the overall noise at the output of the algorithm. Set  holds the operations of the algorithm: additions/subtractions, constant multiplications, multiplications, divisions, and unit delays. Set
holds the operations of the algorithm: additions/subtractions, constant multiplications, multiplications, divisions, and unit delays. Set  contains the signals that interconnect these operations. The FxP format of a number is defined by means of pair
contains the signals that interconnect these operations. The FxP format of a number is defined by means of pair  , where
, where  represents the number of bits from the most significant bit (MSB) to the binary point, and
represents the number of bits from the most significant bit (MSB) to the binary point, and  is the number of total bits (see Figure 1). The FxP format of a signal requires two FxP formats: the format before quantization—(
is the number of total bits (see Figure 1). The FxP format of a signal requires two FxP formats: the format before quantization—( )—and the format after quantization—
)—and the format after quantization— (see [6]). The quantization of the signal is performed only if these two formats are not equal. Initially, the FxP format of signals is unknown and it is the task of WLO to find a suitable set that minimizes the total cost. The FxP format, not only determines the quantization error generated by a quantized signal, but also the number of bits of each signal, and, therefore, the size of the required hardware resources. The size of a resource ultimately determines its area, delay and, power. During WLO, the optimization is guided by means of the cost and the output error obtained from the different FxP formats tried through successive iterations.
(see [6]). The quantization of the signal is performed only if these two formats are not equal. Initially, the FxP format of signals is unknown and it is the task of WLO to find a suitable set that minimizes the total cost. The FxP format, not only determines the quantization error generated by a quantized signal, but also the number of bits of each signal, and, therefore, the size of the required hardware resources. The size of a resource ultimately determines its area, delay and, power. During WLO, the optimization is guided by means of the cost and the output error obtained from the different FxP formats tried through successive iterations.
Figure 2 depicts the WLO approach adopted in this work. WLO is composed of the stages of scaling, which determines the set of  , and word-length selection, which determines the set of
, and word-length selection, which determines the set of  . This subdivision allows to simplify WLO, while still providing significant cost reductions.
. This subdivision allows to simplify WLO, while still providing significant cost reductions.
A wrap-around scaling strategy is adopted since it requires less hardware than other approaches (i.e., saturation techniques). After scaling, the values of  are the minimum possible values that avoid the overflow of signals or, at least, those that reduce the likelihood of overflow to a negligible value. A simulation-based approach is used to carry out scaling [7].
are the minimum possible values that avoid the overflow of signals or, at least, those that reduce the likelihood of overflow to a negligible value. A simulation-based approach is used to carry out scaling [7].
Once scaling is performed, the values of  can be fixed during word-length selection. The right side of Figure 2 shows basic blocks for word-length selection. The main idea is to iterate trying different word-length (i.e.,
can be fixed during word-length selection. The right side of Figure 2 shows basic blocks for word-length selection. The main idea is to iterate trying different word-length (i.e.,  ) combinations until the cost is minimized. Each time the word-length of a signal or a group of signals is changed, the word-lengths must be propagated throughout the graph, task referred to as graph conditioning [6], in order to update the rest of word-lengths. The optimizer control block selects the size of the word-lengths using the values of the previous error and cost estimations and decides when the optimization procedure has finished. The first block in the diagram is the extraction of the quantization noise model (parameterization). The role of this block is to generate a model of the quantization noise at the output due to the FxP format of each signal. This enables to perform a quick error estimation within the optimization loop. The implications of using a fast error estimator are twofold. On the one hand, it is possible to reduce WLO time. On the other hand, more complex optimization techniques can be applied in standard computation times.
) combinations until the cost is minimized. Each time the word-length of a signal or a group of signals is changed, the word-lengths must be propagated throughout the graph, task referred to as graph conditioning [6], in order to update the rest of word-lengths. The optimizer control block selects the size of the word-lengths using the values of the previous error and cost estimations and decides when the optimization procedure has finished. The first block in the diagram is the extraction of the quantization noise model (parameterization). The role of this block is to generate a model of the quantization noise at the output due to the FxP format of each signal. This enables to perform a quick error estimation within the optimization loop. The implications of using a fast error estimator are twofold. On the one hand, it is possible to reduce WLO time. On the other hand, more complex optimization techniques can be applied in standard computation times.
4. Quantization Noise Estimation
4.1. Affine Arithmetic
Affine Arithmetic (AA) [31] is an extension of Interval Arithmetic (IA) [29] aimed at the fast and accurate computation of the ranges of signals in a particular mathematical description of an algorithm. Its main feature is that it automatically cancels the linear dependencies of the included uncertainties along the computation path, thus, avoiding the oversizing produced by IA approaches [36]. It has been applied to both, scaling computation [15, 36, 37], and word-length allocation [1, 15, 36]. Also, a modification called Quantized Affine Arithmetic (QAA) has been applied to the computation of limit cycles [38] and dynamic range analysis of quantized LTI algorithms [37].
The mathematical expression of an affine form is

where  is the central value of
is the central value of  , and
, and  and
and  are its
are its  th noise term identifier and amplitude, respectively. In fact,
th noise term identifier and amplitude, respectively. In fact,  represents the interval
represents the interval  , so an affine form describes a numerical domain in terms of a central value and a sum of intervals with different identifiers. Affine operations are those which operate affine forms and produce an affine form as a result. Given the affine forms
, so an affine form describes a numerical domain in terms of a central value and a sum of intervals with different identifiers. Affine operations are those which operate affine forms and produce an affine form as a result. Given the affine forms  ,
,  , and
, and  , the affine operations are
, the affine operations are

These operations suffice to model any LTI algorithm. Differentiable operations can be approximated using a first-order Taylor expansion:

4.2. Proposed Estimator: General Expression
Here, we present a method able to estimate the quantization noise power from a single AA simulation. The noise estimation is not based on (1), since this equation only applies to LTI algorithms in steady state and our proposal is more general, since it covers both LTI algorithms and nonlinear algorithms. Also, the parameterization method does not lead to (2)–(6), since these are aimed at LTI algorithms in steady state.
Noise estimation is based on the assumption that the quantization of a signal  from
from  bits to
bits to  bits can be modeled by the addition of a uniformly distributed white noise with the following statistical parameters [33]:
bits can be modeled by the addition of a uniformly distributed white noise with the following statistical parameters [33]:

This noise model, which is referred to as the discrete noise model, is an extension of the traditional modeling of quantization error as an additive white noise [34, 35] (continuous noise model). In [33], it is shown that the continuous model can produce an error of up to 200% in comparison to the discrete model.
In [11] it was proved that the effect of the deviation from the original behavior of an algorithm with feedback loops can be modelled by adding an affine form  to each signal
to each signal  at each simulation time instant
at each simulation time instant  . The affine form
. The affine form  models a quantization noise with mean
models a quantization noise with mean  and variance
and variance  , if each error term
, if each error term  is assigned a uniform distribution, and it can be expressed as
is assigned a uniform distribution, and it can be expressed as

Thus, it is possible to know at each moment the origin of a particular error term ( ) and the moment when it was generated (
) and the moment when it was generated ( ). The AA-based simulation can be made independent on the particular statistical parameters of each quantization thanks to error term
). The AA-based simulation can be made independent on the particular statistical parameters of each quantization thanks to error term  . This is desirable in order to obtain a parameterizable noise model. This error term encapsulates the mean value and the variance of the error term
. This is desirable in order to obtain a parameterizable noise model. This error term encapsulates the mean value and the variance of the error term  , and now it can be seen as a random variable with variance
, and now it can be seen as a random variable with variance  and mean
and mean  . This is a reinterpretation of AA, since the error terms are not only intervals, but they also have a probability distribution associated. Once the simulation is finished, it is possible to compute the impact of the quantization noise produced by signal
. This is a reinterpretation of AA, since the error terms are not only intervals, but they also have a probability distribution associated. Once the simulation is finished, it is possible to compute the impact of the quantization noise produced by signal  on the output of the algorithms by checking the values of
on the output of the algorithms by checking the values of  (see (7)). This enables the parameterization of the noise. Once the parameterization is performed, the estimation error produced by any combination of
(see (7)). This enables the parameterization of the noise. Once the parameterization is performed, the estimation error produced by any combination of  can be easily assessed replacing all
can be easily assessed replacing all  by the original expression that accounts for the mean and variance (
by the original expression that accounts for the mean and variance ( ), thus enabling a fast estimation of the quantization error. We will see all the process in the next paragraphs.
), thus enabling a fast estimation of the quantization error. We will see all the process in the next paragraphs.
The expression of a given output  of the algorithm with
of the algorithm with  noise sources is
noise sources is

where  is the value of the output of the algorithm using floating-point arithmetic and the summation is the contribution of the quantization noise sources. Note that
is the value of the output of the algorithm using floating-point arithmetic and the summation is the contribution of the quantization noise sources. Note that  is a function that depends on the inputs of the algorithm.
is a function that depends on the inputs of the algorithm.
The error  at the output is
at the output is

The value of the error is formed by a collection of affine forms at each time step  . The power of the quantization noise of the output can be approximated by the Mean Square Error (MSE), which is estimated as the mean value of the expectancy of the power of the summations of the uniform distributions at each time step
. The power of the quantization noise of the output can be approximated by the Mean Square Error (MSE), which is estimated as the mean value of the expectancy of the power of the summations of the uniform distributions at each time step  as in (14). The estimation is performed using an AA simulation during
as in (14). The estimation is performed using an AA simulation during  time steps,
time steps,

This equation relies on the fact that error terms  are uncorrelated to each other, which is a sensible assumption in quantized DSP systems [34, 35]. Also, the uncorrelation between quantization noises enables to express the variance of a summation of random variables as the summation of the variance of each random variable. The two main terms in (14) are developed as follows
are uncorrelated to each other, which is a sensible assumption in quantized DSP systems [34, 35]. Also, the uncorrelation between quantization noises enables to express the variance of a summation of random variables as the summation of the variance of each random variable. The two main terms in (14) are developed as follows


Combining (14), (15) and (16):

Expressions for the mean and variance can be obtained in a similar fashion:

The output noise power (17), as well as the mean and the variance, can be expressed more compactly by using vectors  ,
,  , and matrix
, and matrix  as shown in (19)–(23). Once vectors
as shown in (19)–(23). Once vectors  ,
,  , and matrix
, and matrix  are computed, the estimation of the quantization noise does not require a simulation but the computation of expressions (19)–(21), which is a much faster process,
are computed, the estimation of the quantization noise does not require a simulation but the computation of expressions (19)–(21), which is a much faster process,







The parameterization process is composed of the following steps:
-
(1)
perform a
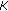 -step AA simulation adding an affine form
-step AA simulation adding an affine form 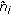 to each signal
to each signal  ,
, -
(2)
compute (22)–(24) using previously collected
 .
.
The error estimation phase can now be executed very quickly by applying (19)–(21).
Please note that
-
(i)
expressions (17)–(22) can be applied to DSP algorithms including differentiable operations (e.g. multiplications, divisions, etc.) by mean of (9) due to the 1st order approximation,
-
(ii)
they are exact for LTI systems in steady state (see the appendix).
4.3. Particularization for LTI Systems
The expressions and the algorithms from the previous subsection can be applied to LTI algorithms, but with a high computational load. In this subsection, we present new expressions to compute the power, mean and variance of the output error for LTI systems in steady state that enable fast estimations.
It is possible to simplify the noise estimation by modifying the expression of the noise terms:

It can also be inferred that

Therefore, it is possible to rewrite the set of (A.1)–(A.3) in order to relate them to the amplitudes of the error terms at the output of the system  as shown in the following
as shown in the following

5. Benchmarks
This section presents the benchmarks used to test the performance of the SQNR estimator. The following benchmarks are used:
-
(i)
RGB to YCrCb converter (RGB) [6],
-
(ii)
8-point IDCT (
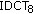 ) [26],
) [26], -
(iii)
2nd-order IIR filter (
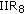 ) [26],
) [26], -
(iv)
3rd-order Lattice filter (
 ) [39],
) [39], -
(v)
6th-order transposed direct form II delta-operator filter (
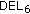 ) [40],
) [40], -
(vi)
3 × 3 vector scalar multiplication (
 ),
), -
(vii)
8 × 8 vector scalar multiplication (
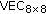 ),
), -
(viii)
MIMO channel equalizer (EQ) [41],
-
(ix)
a mean power estimator based on a 1st IIR filter (POW),
-
(x)
1st-order LMS filter (
 ) [12],
) [12], -
(xi)
2nd-order LMS filter (
 ) [12],
) [12], -
(xii)
5th-order LMS filter (
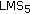 ) [12],
) [12], -
(xiii)
3rd-order Volterra adaptive filter (
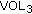 )[42].
)[42].
The main features of the benchmarks are summarized in Table 2, which contains the type of algorithm (LTI or nonlinear, with or without loops), the number of inputs/outputs, the number and type of operations involved, and the total number of signals  . The set of benchmarks covers both LTI and nonlinear algorithms, as well as cyclic and acyclic ones. It must be noted that the set of operations is quite complete since it includes additions, multiplications, and also divisions, usually neglected in similar research studies. In addition to that, it is interesting to highlight that the algorithms are not limited to linear filtering, but they also address 4 G MIMO channel equalizing, vector multiplications and adaptive filtering for both linear and nonlinear system identification.
. The set of benchmarks covers both LTI and nonlinear algorithms, as well as cyclic and acyclic ones. It must be noted that the set of operations is quite complete since it includes additions, multiplications, and also divisions, usually neglected in similar research studies. In addition to that, it is interesting to highlight that the algorithms are not limited to linear filtering, but they also address 4 G MIMO channel equalizing, vector multiplications and adaptive filtering for both linear and nonlinear system identification.
All benchmarks are fed with 16-bit inputs and 12-bit constants and the noise constraint is an SQNR ranging from 40 to 120 dB. The inputs used to perform the noise parameterization as well as the fixed-point simulation are summarized in the last column of the table.
6. Results
The procedure to carry out the tests is as follows:
-
(1)
compute scaling by means of a floating point simulation,
-
(2)
extract noise parameters (22)–(24) performing an AA-based simulation,
-
(3)
perform a WPO as in Figure 2 using a gradient-descent approach,
-
(4)
perform a single FxP bit-true simulation and use it as reference to compute the performance and accuracy of the estimator.
The accuracy obtained by means of a gradient-descent optimization [6] under different SQNR constraints—80 in total, from 40 dB to 120 dB—for the different benchmarks is presented in Table 3. The first column indicates the benchmark used. The remaining columns show the accuracy of the estimations measured in terms of the maximum absolute value of the relative error in dB, and the average of the absolute value of the percentage error, for four SQNR ranges: (120,100) dB, (100,80) dB, (80,60) dB and  dB (see the expressions of the metrics at the bottom of the table).
dB (see the expressions of the metrics at the bottom of the table).
The results yield that the estimator is extremely accurate for LTI algorithms. The mean percentage error is smaller than 1.16%, and the maximum relative error is smaller than 0.24 dB. The quality of the estimates is homogenous within the range  dB.
dB.
The accuracy for nonlinear algorithms shows some degradation. This is expected, since a 1st-order Taylor approximation has been applied (9) in the computation of the quantization noise. Moreover, the presence of loops increases the error in the estimation, since the error due to neglecting Taylor series terms is amplified through the feedback loops. The nonlinear algorithms without loops perform significantly well. The mean percentage error is smaller than 1.52%, and the maximum relative error is smaller than 0.3 dB. This performance is similar to that of LTI algorithms.
The nonlinear algorithms that contain loops have a clearly different behaviour. The mean percentage error is smaller than 16.7%, and the maximum relative error is smaller than 1.43 dB. Now, the accuracy decreases as long as the error constraints get looser. This is due to the aforementioned amplification of the Taylor error terms and also to the fact that the uniformly distributed model for the quantization noise does not remain valid for small SQNRs. The errors due to the quantization noise model introduced by the SQNR ranges used for these experiments are minimum, but, after being propagated through the feedback loops and amplified due to nonlinearities, they become much more noticeable. Anyway, the quality of the estimates is still very high.
The average percentage error is 3.52% which confirms the excellent accuracy obtained by our estimator.
Table 4 holds the performance results in terms of computation times. The first column shows the names of the benchmarks. The second and third columns show the length of the input vectors required for a fixed-point simulation and for the parameterization process. The parameterization time is in the fourth column. The average number of iterations required during the optimization process is in the fifth column. The next two columns present the computation time required to perform the gradient-descent optimization using our estimation-based proposal and using a classical simulation-based approach. The computation time for the simulation-based approach is, in fact, an estimation, based on multiplying the average number of optimization iterations by the computation time of a single fixed-point simulation. Finally, the speed-up obtained by our estimation-based approach is presented in the last column.
The parameterization time goes from 160  secs. to 28 mins. (1646 secs.), and it depends on the size of the input data, the complexity of the algorithm (i.e., number and types of operations), and the presence of loops. The
secs. to 28 mins. (1646 secs.), and it depends on the size of the input data, the complexity of the algorithm (i.e., number and types of operations), and the presence of loops. The  benchmarks clearly show how the parameterization time is increased as long as the number of delays, and therefore loops, increases. These times might seem quite long, but it must be born in mind that the parameterization process is performed only once, and after that the algorithm can be assigned a fixed-point format as many times as desired using the fast estimator.
benchmarks clearly show how the parameterization time is increased as long as the number of delays, and therefore loops, increases. These times might seem quite long, but it must be born in mind that the parameterization process is performed only once, and after that the algorithm can be assigned a fixed-point format as many times as desired using the fast estimator.
The mean number of estimates in the fifth column is shown to give an idea of the complexity of the optimization process. A simulation-based optimization approach would require that very same number of simulations, thus taking a very long time. For instance, the optimization of  would approximately require 2500 FxP simulations of 5000 input data. Considering the number of estimations required, the optimization times are extremely fast, ranging from 0.02 secs to 7.26 secs. The speedups obtained in comparison to a simulation-based approach are staggering; boosts from ×221 to ×3235 are obtained. The average boost is ×1486 which proves the advantage of our approach in terms of computation time.
would approximately require 2500 FxP simulations of 5000 input data. Considering the number of estimations required, the optimization times are extremely fast, ranging from 0.02 secs to 7.26 secs. The speedups obtained in comparison to a simulation-based approach are staggering; boosts from ×221 to ×3235 are obtained. The average boost is ×1486 which proves the advantage of our approach in terms of computation time.
In summary, results show that our approach enables fast and accurate WLO of both LTI and nonlinear DSP algorithms.
7. Conclusions
A novel noise estimation method based on the use of Affine Arithmetic has been presented. This method allows to obtain fast and accurate estimates of the quantization noise at the output of the FxP description of a DSP algorithm. The estimator can be used to perform complex WLO in standard time, leading to significant hardware cost reductions. The method can be applied to differentiable nonlinear DSP algorithms with and without feedbacks.
In brief, the main contributions of the paper are
-
(i)
the proposal of a novel AA-based quantization noise estimation for LTI algorithms,
-
(ii)
the proposal of a novel AA-based quantization noise estimation for nonlinear algorithms with and without feedbacks,
-
(iii)
the average estimation error for LTI systems is smaller than 2%,
-
(iv)
the average estimation error for nonlinear systems is smaller than 17%,
-
(v)
the computation time of WLO is boosted up to ×3235 (average of ×1486),
The reduction of the computation time of the noise parameterization process, specially in the presence of loops, is to be approached in the near future. Also, the improvement of the quantization model for nonlinear operations is perceived as an interesting research line.
References
Fang CF, Chen T, Rutenbar RA: Floating-point error analysis based on affine arithmetic. IEEE International Conference on Accoustics, Speech, and Signal Processing, April 2003, Hong Kong 561-564.
Gaffar A, Mencer O, Luk W, Cheung P, Shirazi N: Floating-point bitwidth analysis via automatic differentiation. International Conference on Field Programmable Technology, 2002 158-165.
Gaffar AA, Mencer O, Luk W, Cheung PYK: Unifying bit-width optimisation for fixed-point and floating-point designs. Proceedings of the 12th Annual IEEE Symposium on Field-Programmable Custom Computing Machines (FCCM '04), April 2004 79-88.
Caffarena G, Constantinides GA, Cheung PYK, Carreras C, Nieto-Taladriz O: Optimal combined word-length allocation and architectural synthesis of digital signal processing circuits. IEEE Transactions on Circuits and Systems II 2006, 53(5):339-343.
Catthoor F, De Man H, Vandewalle J: Simulated annealing based optimization of coefficient and data word-lengths in digital filters. International Journal of Circuit Theory and Applications 1988, 16(4):371-390. 10.1002/cta.4490160404
Constantinides GA, Cheung PYK, Luk W: Wordlength optimization for linear digital signal processing. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2003, 22(10):1432-1442. 10.1109/TCAD.2003.818119
Sung W, Kum K: Simulation-based word-length optimization method for fixed-point digital signal processing systems. IEEE Transactions on Signal Processing 1995, 43(12):3087-3090. 10.1109/78.476465
Constantinides GA, Woeginger GJ: The complexity of multiple wordlength assignment. Applied Mathematics Letters 2002, 15(2):137-140. 10.1016/S0893-9659(01)00107-0
Caffarena G, Fernandez A, Carreras C, Nieto-Taladriz O: Fixed-point refinement of OFDM-based adaptive equalizers: a heuristic approach. European Signal Processing Conference, 2004 1353-1356.
Cantin M-A, Savaria Y, Lavoie P: A comparison of automatic word length optimization procedures. IEEE International Symposium on Circuits and Systems, May 2002 612-615.
López JA, Caffarena G, Carreras C, Nieto-Taladriz O: Fast and accurate computation of the round-off noise of linear time-invariant systems. IET Circuits, Devices and Systems 2008, 2(4):393-408. 10.1049/iet-cds:20070198
Constantinides G: Perturbation analysis for word-length optimization. IEEE Symposium on Field-Programmable Custom Computing Machines, 2003 81-90.
Menard D, Rocher R, Scalart P, Sentieys O: SQNR determination in non-linear and non-recursive fixed-point systems. European Signal Processing Conference, 2004 1349-1352.
Shi C, Brodersen RW: A perturbation theory on statistical quantization effects in fixed-point DSP with non-stationary inputs. Proceedings of IEEE International Symposium on Circuits and Systems, May 2004, Vancouver, Canada 3: 373-376.
Lee D-U, Gaffar AA, Cheung RCC, Mencer O, Luk W, Constantinides GA: Accuracy-guaranteed bit-width optimization. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2006, 25(10):1990-1999.
Menard D, Sentieys O: A methodology for evaluating the precision of fixed-point systems. IEEE International Conference on Acoustic, Speech, and Signal Processing, May 2002 3152-3155.
Rocher R, Menard D, Herve N, Sentieys O: Fixed-point configurable hardware components. EURASIP Journal on Embedded Systems 2006, 2006:-13.
Kim S, Kum K-II, Sung W: Fixed-point optimization utility for C and C++ based digital signal processing programs. IEEE Transactions on Circuits and Systems II 1998, 45(11):1455-1464. 10.1109/82.735357
Willems M, Keding H, Grótker T, Meyr H: FRIDGE: an interactive fixed-point code generation environment for Hw/Sw-codesign. IEEE Conference on Acoustics, Speech and Signal Processing, 1997, Munich, Germany 687-690.
Chang M, Hauck S: Precis: a design-time precision aanalysis tool. IEEE Symposium on Field-Programmable Custom Computing Machines, 2002 229-238.
Chang ML, Hauck S: Précis: a usercentric word-length optimization tool. IEEE Design and Test of Computers 2005, 22(4):349-361. 10.1109/MDT.2005.92
Cmar R, Rijnders L, Schaumont P, Vernalde S, Bolsens I: A methodology and design environment for DSP ASIC fixed point refinement. Proceedings of the Conference on Design, Automation and Test in Europe, 1999 56.
Benedetti A, Perona P: Bit-width optimization for configurable DSP's by multi-interval analysis. Proceedings of the 34th Asilomar Conference on Signals, Systems and Computers, November 2000 355-359.
Mahlke S, Ravindran R, Schlansker M, Schreiber R, Sherwood T: Bitwidth cognizant architecture synthesis of custom hardware accelerators. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2001, 20(11):1355-1371. 10.1109/43.959864
Stephenson M, Babb J, Amarasinghe S: Bitwidth analysis with application to silicon compilation. SIGPLAN Conference on Programming Language Design and Implementation (PLDI '00), June 2000 108-120.
Fang CF, Rutenbar RA, Chen T: Fast, accurate static analysis for fixed-point finite-precision effects in DSP designs. IEEE/ACM International Conference on Computer Aided Design (ICCAD '03), November 2003 275-282.
López JA, Caffarena G, Carreras C, Nieto-Taladriz O: Characterization of the quantization properties of similarity-related DSP structures by means of interval simulations. Proceedings of the 37th Asilomar Conference on Signals, Systems and Computers, November 2003 2208-2212.
Wadekar SA, Parker AC: Accuracy sensitive word-length selection for algorithm optimization. Proceedings of the IEEE International Conference on Computer Design, October 1998 54-61.
Hayes B: A lucid interval. American Scientist 2003, 91(6):484-488.
Carreras C, López JA, Nieto-Taladriz O: Bit-width selection for data-path implementations. International Symposium on System Synthesis, 1999 114.
Stolfi J, Figueiredo LH: Self-Validated Numerical Methods and Applications. In Brazilian Mathematics Colloquium Monograph. IMPA, Rio de Janeiro, Brazil; 1997.
Oppenheim AV, Schafer RW: Discrete-Time Signal Processing. Prentice-Hall, Englewood Cliffs, NJ, USA; 1987.
Constantinides GA, Cheung PYK, Luk W: Truncation noise in fixed-point SFGs. Electronics Letters 1999, 35(23):2013-2014.
Jackson LB: Roundoff-noise analysis for fixed-point digital filters realized in cascade or parallel form. IEEE Transactions on Audio and Electroacoustics 1970, 18(2):107-122. 10.1109/TAU.1970.1162084
Oppenheim AV, Weinstein CJ: Effects of finite register length in digital filtering and the fast Fourier transform. Proceedings of the IEEE 1972, 60(8):957-976.
López J: Evaluación de los Efectos de Cuantificación en las Estructuras de Filtros Digitales Mediante Técnicas de Simulación Basadas en Extensiones de Intervalos, Ph.D. thesis. Universidad Politécnica de Madrid; 2004.
López JA, Carreras C, Nieto-Taladriz O: Improved interval-based characterization of fixed-point LTI systems with feedback loops. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2007, 26(11):1923-1933.
Lopez J, Caffarena G, Carreras C, Nieto-Taladriz O: Analysis of limit cycles by means of affine arithmetic computer-aided tests. European Signal Processing Conference, 2004 991-994.
Parhi KK: VLSI Digital Signal Processing Systems: Design and Implementation. Wiley, New York, NY, USA; 1999.
Li G, Zhao Z: On the generalized DFIIt structure and its state-space realization in digital filter implementation. IEEE Transactions on Circuits and Systems I 2004, 51(4):769-778. 10.1109/TCSI.2004.823652
Fernandez Herrero A, Jiménez-Pacheco A, Caffarena G, Casajus Quiros J: Design and implementation of a hardware module for equalisation in a 4G mimo receiver. International Conference on Field Programmable Logic and Applications (FPL '06), August 2006 765-768.
Ogunfunmi T: Adaptive Nonlinear System Identification: The Volterra and Wiener Approaches. Springer; 2007.
Acknowledgments
The authors would like to thank the work of the anonymous reviewers. This work was supported by the Spanish Ministry of Science and Innovation under project TEC2009-14219-C03-02.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Validity of General Expression for Steady-State LTI Algorithms
Expressions (17)–(22) can be applied to DSP algorithms including differentiable operations (e.g., multiplications, divisions, etc.) by means of (9), due to the 1st-order approximation. However, they should be exact for LTI systems and match the well-known expressions for LTI algorithms in steady state,



where  and
and  are the transfer function and the impulse response from signal
are the transfer function and the impulse response from signal  to the output of the algorithm, respectively. The LTI system is supposed to be causal (
to the output of the algorithm, respectively. The LTI system is supposed to be causal ( ) and stable (
) and stable ( ).
).
In LTI systems, the coefficients  multiplying each
multiplying each  depend only on
depend only on  and are equal to
and are equal to

Equation (17) turns into

Note that (A.1)–(A.3) assume that the LTI system is in steady state. Therefore, the transient must be removed from the computation of the MSE. Hereby, (A.5) only matches (A.3), if the affine simulation is performed during  iterations (
iterations ( ), where
), where  is such that for all
is such that for all  , and the first
, and the first  iterations
iterations  are removed from the computation. Thus,
are removed from the computation. Thus,

Similarly, (18) can be matched to (A.1) and (A.2), respectively, thus validating the approach for LTI algorithms.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Caffarena, G., Carreras, C., López, J.A. et al. SQNR Estimation of Fixed-Point DSP Algorithms. EURASIP J. Adv. Signal Process. 2010, 171027 (2010). https://doi.org/10.1155/2010/171027
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/171027


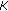 -step AA simulation adding an affine form
-step AA simulation adding an affine form 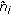 to each signal
to each signal  ,
, .
.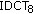 ) [
) [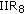 ) [
) [ ) [
) [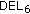 ) [
) [ ),
),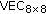 ),
), ) [
) [ ) [
) [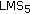 ) [
) [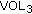 )[
)[