- Research Article
- Open access
- Published:
Robust Blind Frequency and Transition Time Estimation for Frequency Hopping Systems
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 172703 (2010)
Abstract
In frequency hopping spread spectrum (FHSS) systems, two major problems are timing synchronization and frequency estimation. A blind estimation scheme is presented for estimating frequency and transition time without using reference signals. The scheme is robust in the sense that it can avoid the unbalanced sampling block problem that occurs in existing maximum likelihood-based schemes, which causes large errors in one of the estimates of frequency. The proposed scheme has a lower computational cost than the maximum likelihood-based greedy search method. The estimated parameters are also used for the subsequent time and frequency tracking. The simulation results demonstrate the efficacy of the proposed approach.
1. Introduction
Frequency hopping spread spectrum (FHSS) techniques are widely used in military communications for combating narrowband interference and for security purposes. The two parameters that are required for the estimation in FHSS are transition time and hopping frequency. Regular synchronization is divided into two stages—coarse acquisition and fine tracking [1]. Reference signals may be used to estimate the parameters [2–6], but they may not be available in all cases. Moreover, since the usage of reference signals requires bandwidth, it reduces the bandwidth efficiency. To improve spectral utilization, several researchers [7–13] have proposed some algorithms for blind estimation. Liang et al. [7] proposed a revisable jump Markov chain Monte Carlo-(RJMCMC-) based algorithm for estimating frequency and timing parameters. However, it requires that the hyperparameter is known in advance. Liu et al. [8] used an antenna array and the expectation-maximization (EM) algorithm to estimate multiple FH signals, but the computational complexity was high. Mallat and Zhang [10] used the matching pursuit (MP) method that decomposes the signal into a linear expansion of time-frequency components; however, this algorithm needs to select a discrete subset of possible dictionary functions for practical implementation [10]. Liu et al. [11] proposed a joint hop-timing and frequency estimation method that was based on the principle of dynamic programming (DP) coupled with 2D harmonic retrieval (HR) using antenna arrays. The complexity of the DP algorithm is roughly a fourth-order polynomial in the number of temporal signal snapshots. A stochastic modeling and particle filtering-based algorithm has been proposed by using a state-space model to solve nonlinear and non-Gaussian signals [12]. Ko et al. [13] proposed a blind maximum likelihood- (ML-) based iterative algorithm for frequency estimation and synchronization using a two-hop model; however, it yielded more than one solution, raising the problem of convergence to the solution that is associated with the hopping frequency. The authors [8] also pointed out that whether the approach of Ko et al.[13] can guarantee identifiability for the frequency estimation. Additionally, in the ML-based estimation approach, if the transition time in the processing data block between two hopping frequencies is close to the boundary value, then the data block is in an unbalance situation of sampled signals in the frequency components. In this scenario, the performance of one estimation of frequency is severely degraded.
This investigation presents a blind frequency estimation and timing synchronization algorithm. The approach is resistant to the aforementioned problem of unbalance. It reduces the computational load by using a proposed iterative method compared to a maximum likelihood-based greedy search method.
The rest of this paper is organized as follows. Section 2 introduces signal model and the problem formulation. In Section 3, the proposed algorithm for estimating frequencies and transition time is derived. Section 4 presents the computational complexity. Section 5 presents the computer-simulated results. Finally, Section 6 draws conclusions.
2. Signal Model and Problem Formulation
In this section, the signal model of FHSS is analyzed and the mathematical form of a likelihood function is derived. The two-hop signal model for frequency hopping can be expressed as

where  and
and  are the hopping frequencies,
are the hopping frequencies,  is the sampling period, and
is the sampling period, and  is the hopping period [13].
is the hopping period [13].
The received signal in an interval of  can be written as
can be written as

where  represent the channel gains of the
represent the channel gains of the  hop through the transmitting path and
hop through the transmitting path and  is an added white Gaussian noise (AWGN) with zero mean and variance
is an added white Gaussian noise (AWGN) with zero mean and variance  . The problem of determining
. The problem of determining  in (2) is thus equivalent to solving the timing synchronization problem.
in (2) is thus equivalent to solving the timing synchronization problem.
Rewriting the received signal in vector form yields

where

To simplify the analysis,  can be partitioned into two components that correspond to individual hops as follows:
can be partitioned into two components that correspond to individual hops as follows:

where

The likelihood function of the received signal is

The parameters  can be estimated by maximizing (7), which is equivalent to minimizing the objective function
can be estimated by maximizing (7), which is equivalent to minimizing the objective function

where


Since  and
and  of (8) are positive, minimizing (8) after some manipulation yields the estimated frequency
of (8) are positive, minimizing (8) after some manipulation yields the estimated frequency  :
:

where

Similarly, minimizing (10) yields  :
:

where

Equations (11) and (13) indicate that frequencies  and
and  can be estimated by maximizing
can be estimated by maximizing  and
and  , respectively. The maximization of the two functions can be regarded as finding
, respectively. The maximization of the two functions can be regarded as finding  and
and  that maximize the values of
that maximize the values of  ,
,  projected into the received signals
projected into the received signals  and
and  .
.
Finally, given the derived equations (11) and (13), the objective function of minimizing (8) is equivalent to the maximization of the objective function

where

Since the transition time  is not known in advance, every possible
is not known in advance, every possible  and the estimates of the two frequencies
and the estimates of the two frequencies  should be tried in ML-based greedy search approaches. The ML estimation of
should be tried in ML-based greedy search approaches. The ML estimation of  can be performed using
can be performed using

3. Proposed Estimation Algorithm Based on Maximum Likelihood Principle
The blind estimation scheme is developed in this section. The processing of the proposed scheme is divided into the synchronization phase and the tracking phase for parameter estimation. The details are as follows.
3.1. Synchronization Phase
Based on the analysis in Section 2, solving (8) is clearly a multivariable estimation problem ( ,
,  and
and  ). To estimate frequencies
). To estimate frequencies  and
and  accurately,
accurately,  must be estimated correctly. On the other hand, the accurate estimation of
must be estimated correctly. On the other hand, the accurate estimation of  depends on sufficiently accurate estimates of frequencies
depends on sufficiently accurate estimates of frequencies  and
and  . The most fundamental approach for solving this problem is a maximum likelihood-based greedy search approach, in which estimates are made by scanning the frequency and the transition time simultaneously, and finding the values of the frequency and time that maximize (8). However, the greedy search approach has an extremely large computational complexity although it may yield the optimal solution in some sense.
. The most fundamental approach for solving this problem is a maximum likelihood-based greedy search approach, in which estimates are made by scanning the frequency and the transition time simultaneously, and finding the values of the frequency and time that maximize (8). However, the greedy search approach has an extremely large computational complexity although it may yield the optimal solution in some sense.
To deliver competitive performance but reduce the computational load, the proposed algorithm is developed as an iterative approach by modifying the concept of the alternative projection algorithm that was proposed by Ziskind and Wax [14]. Essentially, the approach converts a multivariable problem into a single variable problem and thereby reduces the computational load. The algorithm differs from that of Ziskind and Wax [14] and must be adapted to the FHSS problem. The proposed approach does not depend the complex matrix inverse calculation but simply applies a basic vector computation (inner product), which further reduces the computational complexity.
In iterating the proposed scheme, the maximization is only conducted on one variable while the other variables are held constant. For instance,  may be fixed first and the
may be fixed first and the  and
and  that maximize the objective function are computed; after
that maximize the objective function are computed; after  and
and  have been estimated,
have been estimated,  and
and  are fixed and then
are fixed and then  is estimated. After many iterations, the estimates of
is estimated. After many iterations, the estimates of  , and
, and  can be obtained.
can be obtained.
Since the transition time  is unknown in advance, an initial value of
is unknown in advance, an initial value of  , denoted as
, denoted as  , is set, where the number in the superscript bracket stands for the iteration number and the overscript with the sign of a hat stands for "estimated value." For example,
, is set, where the number in the superscript bracket stands for the iteration number and the overscript with the sign of a hat stands for "estimated value." For example,  denotes the estimated value of
denotes the estimated value of  in the initialization. Since
in the initialization. Since  is unknown in advance, the initial estimate
is unknown in advance, the initial estimate  can be selected based on the minimization of the initial estimation mean squared error in a statistical sense.
can be selected based on the minimization of the initial estimation mean squared error in a statistical sense.  is a random variable with a uniform distribution. The expectation of the random variable is
is a random variable with a uniform distribution. The expectation of the random variable is . Therefore, the initial estimate
. Therefore, the initial estimate  minimizes the mean squared error. The initial value
minimizes the mean squared error. The initial value  can be set to
can be set to  .
.
With the initial value of  known, the estimated values of
known, the estimated values of  and
and  can be obtained by the maximization as
can be obtained by the maximization as

Next, the estimated frequencies  and
and  are fixed, and
are fixed, and  is calculated by
is calculated by

where


Based on the above development,  ,
,  , and
, and  can be estimated by fixing the values of the other parameters in each iteration. Notably, the value given by (20) obtained by utilizing the proposed processing procedure is monotonically increasing during the iteration. After a few iterations, it converges to a local maximum, and the local maximum may or may not be the global maximum.
can be estimated by fixing the values of the other parameters in each iteration. Notably, the value given by (20) obtained by utilizing the proposed processing procedure is monotonically increasing during the iteration. After a few iterations, it converges to a local maximum, and the local maximum may or may not be the global maximum.
3.2. Robust Estimation in the Synchronization Phase
Although the estimates of  ,
,  , and
, and  can be obtained using the proposed scheme or other ML-based schemes, such as the exhaustive search method, if the transition time of the received signal is close to the boundary of the sampling data block, then one of the frequency estimation errors would be large, because the samples used in the estimation of one frequency are small. To eliminate this problem and improve performance, an attempt can be made to shift the sampling data block for processing in each iteration. This action is equivalent to adjusting the transition time
can be obtained using the proposed scheme or other ML-based schemes, such as the exhaustive search method, if the transition time of the received signal is close to the boundary of the sampling data block, then one of the frequency estimation errors would be large, because the samples used in the estimation of one frequency are small. To eliminate this problem and improve performance, an attempt can be made to shift the sampling data block for processing in each iteration. This action is equivalent to adjusting the transition time  by shifting, and this value is expected to be close to
by shifting, and this value is expected to be close to  as in a balanced situation. In each iteration, the sampling position of the data block is shifted by
as in a balanced situation. In each iteration, the sampling position of the data block is shifted by

When the difference between the initial values of  and true
and true  is large, the estimation may be erroneous. For example, only one estimated frequency would be obtained because the duration of the signal with a single frequency component would dominate the whole sample block. The problem is remedied by making the following proposed modification. Since (11) and (13) are derived by assuming that the true
is large, the estimation may be erroneous. For example, only one estimated frequency would be obtained because the duration of the signal with a single frequency component would dominate the whole sample block. The problem is remedied by making the following proposed modification. Since (11) and (13) are derived by assuming that the true  is known, both equations can be treated as two separated functions of only one frequency signal in each subblock such that
is known, both equations can be treated as two separated functions of only one frequency signal in each subblock such that  ,
,  can be estimated using (11) and (13), respectively. However, in practice, the transition time
can be estimated using (11) and (13), respectively. However, in practice, the transition time  in (11) and (13) is obtained from the estimation of
in (11) and (13) is obtained from the estimation of  . If
. If  , then one of the two subblocks contains both frequencies
, then one of the two subblocks contains both frequencies  and
and  and the other subblock contains only one frequency component. With reference to Figure 1, if
and the other subblock contains only one frequency component. With reference to Figure 1, if  , (11) and (13) become
, (11) and (13) become


where

Since  in (23) contains both frequencies
in (23) contains both frequencies  and
and  , the expression in the
, the expression in the  operation of (23) becomes
operation of (23) becomes

According to (26), when  , the expression contains the desired signal
, the expression contains the desired signal  , noise, and an interference portion
, noise, and an interference portion  . Therefore, if
. Therefore, if  is estimated using (26), then the estimation frequency error would depend on the difference
is estimated using (26), then the estimation frequency error would depend on the difference  and the noise. Additionally, since (26) contains both
and the noise. Additionally, since (26) contains both  and
and  , two peaks that correspond to
, two peaks that correspond to  and
and  are identified in frequency scanning. Therefore, the initial value
are identified in frequency scanning. Therefore, the initial value  would affect the performance of the estimation. To solve this problem,
would affect the performance of the estimation. To solve this problem,  can be adjusted close to
can be adjusted close to  . The task is achieved by performing the following operation.
. The task is achieved by performing the following operation.
If  (or
(or  ), then the estimate of
), then the estimate of  from the signal subblock may becomes
from the signal subblock may becomes  (or
(or  to be estimated erroneously as
to be estimated erroneously as  ). The results of the estimation would have approximately the same value:
). The results of the estimation would have approximately the same value:  , (if the channel gains of the two frequencies are assumed to be approximately the same as for regular applied systems). To solve the problem of
, (if the channel gains of the two frequencies are assumed to be approximately the same as for regular applied systems). To solve the problem of  , a method is proposed in which the value
, a method is proposed in which the value  is adjusted close to
is adjusted close to  by shifting forward and backward the received signal
by shifting forward and backward the received signal  with
with  , when the frequency estimation condition
, when the frequency estimation condition  is met. (The reason for choosing
is met. (The reason for choosing  will be explained below.)
will be explained below.)
Consider the situation  . Since the goal is to obtain
. Since the goal is to obtain  for a balanced situation,
for a balanced situation,  is substituted into
is substituted into  yielding the inequality
yielding the inequality  . Hence, the situation of
. Hence, the situation of  may occur if
may occur if  . The transition time
. The transition time  of the received signal in a selected sample block is a random variable. When
of the received signal in a selected sample block is a random variable. When  , the received signal block should be adjusted backward by
, the received signal block should be adjusted backward by samples. Following this adjustment, the transition time may fall in the range of
samples. Following this adjustment, the transition time may fall in the range of  ; a similar adjustment can be applied when
; a similar adjustment can be applied when  . Substituting
. Substituting  yields
yields  . The received signal block should be adjusted forward by
. The received signal block should be adjusted forward by samples, and the transition time may fall in the range
samples, and the transition time may fall in the range  .
.
Finally, when  ,
,  or
or  may occur. The forward and backward adjustments of the received signal block with
may occur. The forward and backward adjustments of the received signal block with  yield the two shifted versions of
yield the two shifted versions of  :
:

The block that has two peaks with similar power in the frequency domain may be chosen to determine whether  is close to
is close to  for the sample block. The decision rule is expressed as
for the sample block. The decision rule is expressed as

where  ,
,  ,
,  , and
, and  are the first and the second largest power values in blocks
are the first and the second largest power values in blocks  and
and  , respectively. The estimates can be made by performing the DFT operations.
, respectively. The estimates can be made by performing the DFT operations.
3.3. Tracking Phase
Once the timing of the received signal is determined, the frequency can be estimated by receiving every upcoming  sample. However, Owing to timing jitter and possible hostile communication scenarios, it is necessary to track the timing and frequencies of upcoming data samples. The following processing step is proposed. Figure 2 presents the process in which the received signal is fed into the registers. The registries contain
sample. However, Owing to timing jitter and possible hostile communication scenarios, it is necessary to track the timing and frequencies of upcoming data samples. The following processing step is proposed. Figure 2 presents the process in which the received signal is fed into the registers. The registries contain  samples and two buffers, each associated with
samples and two buffers, each associated with  samples, which are used to adjust
samples, which are used to adjust  .
.
Since the parameters  , and
, and  in the preceding block are obtained,
in the preceding block are obtained,  in the previous block becomes
in the previous block becomes  in the upcoming data block. Hence, the estimated
in the upcoming data block. Hence, the estimated  and
and  are adopted in the following estimation operation:
are adopted in the following estimation operation:






Since  is adjusted close to
is adjusted close to  in the synchronization phase, in this phase, the received signal
in the synchronization phase, in this phase, the received signal  has a balanced block, and the iteration number
has a balanced block, and the iteration number  can be set. The previous estimate of
can be set. The previous estimate of  is used to estimate
is used to estimate  in the upcoming block. Therefore, the estimation of
in the upcoming block. Therefore, the estimation of  is eliminated. Notably, in (32), only
is eliminated. Notably, in (32), only  samples are utilized to estimate the frequency to reduce the computational load and save time for the subsequent system operation. (In the hostile communication environment, e.g., a jammer/interfering operation may follow the estimation task.) However, if accuracy of the frequency estimation is paramount, then all
samples are utilized to estimate the frequency to reduce the computational load and save time for the subsequent system operation. (In the hostile communication environment, e.g., a jammer/interfering operation may follow the estimation task.) However, if accuracy of the frequency estimation is paramount, then all  samples may be adopted to perform the frequency estimation. It would rely on the type of the application, and using whole
samples may be adopted to perform the frequency estimation. It would rely on the type of the application, and using whole  or
or  sample for estimation is a trade-off between the computational complexity and the estimation accuracy.
sample for estimation is a trade-off between the computational complexity and the estimation accuracy.
Algorithm Summary
The steps in the proposed algorithm are summarized as follows.
Step 1 (synchronization phase). (1) Receive  signal samples
signal samples  and input the data to the registers and the buffers.
and input the data to the registers and the buffers.
(2) Perform the preprocessing procedure to estimate frequencies and  .
.
-
(A)
Set
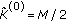 and estimate the frequencies that maximize
and estimate the frequencies that maximize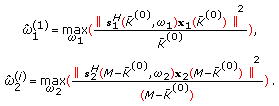 (35)
(35) -
(B)
If
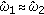 , then shift
, then shift  forward and backward, yielding two blocks,
forward and backward, yielding two blocks,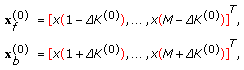 (36)
(36)where
 . Then, select one of the two blocks by applying the following decision rule:
. Then, select one of the two blocks by applying the following decision rule: (37)
(37)Go to (A).
-
(C)
Estimate
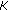 using
using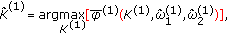 (38)
(38)where
 (39)
(39) -
(D)
Shift by
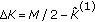
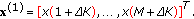 (40)
(40)
(3) For  , perform iterations to estimate frequencies and
, perform iterations to estimate frequencies and 
-
(A)
Set
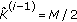 and estimate the frequencies that maximize
and estimate the frequencies that maximize (41)
(41) -
(B)
Estimate
 using
using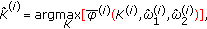 (42)
(42)where
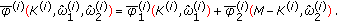 (43)
(43) -
(C)
Shift by
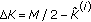
 (44)
(44)
Step 2 (tracking phase). (1) Input the next  samples to the registers.
samples to the registers.
(2) Use the estimated parameter  and
and  (which is set to the estimated
(which is set to the estimated  of the previous block) to compute the following.
of the previous block) to compute the following.
(A) Find the frequency estimate that maximizes

(B) Next, fix the frequency estimates and find  that maximizes
that maximizes

(C) Shift by  to obtain
to obtain

4. Analysis of Computational Complexity
The Big-Oh notation is a well-accepted approach for analyzing the computational complexities of algorithms and is adopted. The computational complexity is analyzed in detail as follows. Let  be the number of frequency scanning points, which is related to the frequency scanning resolution and is typically much larger than
be the number of frequency scanning points, which is related to the frequency scanning resolution and is typically much larger than  .
.
In the ML greedy search scheme, every possible  and the estimates of the two frequencies
and the estimates of the two frequencies  should be tried. For each possible transition time that is used to evaluate
should be tried. For each possible transition time that is used to evaluate  in (17), the computational complexity of the multiplication operations is
in (17), the computational complexity of the multiplication operations is  , where
, where  is the number of points and the two subvectors of sizes
is the number of points and the two subvectors of sizes  and
and  are involved in the operation. The computational complexity of the addition operations is
are involved in the operation. The computational complexity of the addition operations is  by evaluating
by evaluating  with all paired combinations of the arguments
with all paired combinations of the arguments  and
and  . The selection of arguments in the maximum operation and the other operations has lower complexities and can be neglected when the Big-Oh notation is used. Accordingly, the total computational complexity of the multiplication operations is
. The selection of arguments in the maximum operation and the other operations has lower complexities and can be neglected when the Big-Oh notation is used. Accordingly, the total computational complexity of the multiplication operations is  and that of the addition operations is
and that of the addition operations is  .
.
The proposed approach consists of the synchronization phase and the tracking phase. The multiplication and addition operations in the synchronization phase of the proposed approach are analyzed as follows. Referring to the algorithm summary, Step (A) has a computational complexity of  and Step (B) has a computational complexity of
and Step (B) has a computational complexity of  . Step (B) of the preprocessing adjustment requires an extra
. Step (B) of the preprocessing adjustment requires an extra  complexity because of the two M-point FFT operations. The iterations stop after a fixed small number, which can be regarded as a constant
complexity because of the two M-point FFT operations. The iterations stop after a fixed small number, which can be regarded as a constant  . Therefore, the total computational complexity is
. Therefore, the total computational complexity is  . The computational complexity is lower than that of the ML-based method. Since the transition time
. The computational complexity is lower than that of the ML-based method. Since the transition time  of a received signal is random between 1 and
of a received signal is random between 1 and  , wrong estimates can be made in the unbalanced situation. Thus, the adjustment scheme is proposed herein to prevent such a situation.
, wrong estimates can be made in the unbalanced situation. Thus, the adjustment scheme is proposed herein to prevent such a situation.
Similarly, the computational complexity of the scheme in the tracking phase is  . Although it has the same order of the computational complexity as the synchronization phase; however,
. Although it has the same order of the computational complexity as the synchronization phase; however,  has been adjusted close to
has been adjusted close to  , and only one frequency estimation task is performed. The computational complexity is further reduced, since we can estimate one frequency instead of two frequencies and search for
, and only one frequency estimation task is performed. The computational complexity is further reduced, since we can estimate one frequency instead of two frequencies and search for  that is around
that is around  instead of all possible
instead of all possible  's.
's.
Real-time computing refers to hardware and software systems that are subject to a real-time constraint. The Big-Oh notation is well accepted for analyzing the computational complexity of algorithms. The true computing time of an algorithm varies with the processor, architecture, memory, and operating system used to execute it. Additionally, the computing power of processors continues to increase owing to progress in VLSI technology. When the computational complexity of an algorithm is polynomial time instead of exponential time, that algorithm is feasible for real-time application. Therefore, the concept of computational complexity is adopted herein to judge whether an algorithm is a real-time algorithm. A similar evaluation approach can be found in the literature. The use of parallel processing can also reduce computing time. For example, if  processers are used, each may be assigned to evaluate the cost function of each frequency estimate, as in (18), which can be done separately and in parallel. As analyzed in this investigation, the computational complexity of the proposed scheme is
processers are used, each may be assigned to evaluate the cost function of each frequency estimate, as in (18), which can be done separately and in parallel. As analyzed in this investigation, the computational complexity of the proposed scheme is  , which is polynomial time rather than exponential time. An algorithm with a complexity of
, which is polynomial time rather than exponential time. An algorithm with a complexity of  can be treated as feasible for real-time application.
can be treated as feasible for real-time application.
5. Simulations Results
In this section, numerous simulations are conducted to demonstrate the efficiency of the proposed scheme. The hopping frequencies are set to [ ] Hz, and the channel gains are set to
] Hz, and the channel gains are set to  . The sampling frequency is
. The sampling frequency is  and the hopping period is
and the hopping period is  . The scanning frequency resolution is 50 Hz. To illustrate the convergence property of the proposed algorithm, Figure 3 presents the frequency error and the error in the estimation of the transition time
. The scanning frequency resolution is 50 Hz. To illustrate the convergence property of the proposed algorithm, Figure 3 presents the frequency error and the error in the estimation of the transition time  versus the number of iterations for
versus the number of iterations for  . The simulation results indicate that it converges after about two iterations.
. The simulation results indicate that it converges after about two iterations.
To evaluate performance, the transition time is set to three conditions,  ,
,  , and random
, and random  , generated randomly between 1 and
, generated randomly between 1 and  with a uniform distribution. The Cramer Rao lower bound (CRLB) for the balance block (
with a uniform distribution. The Cramer Rao lower bound (CRLB) for the balance block ( ) is also provided for comparison. (It is derived in the appendix.).
) is also provided for comparison. (It is derived in the appendix.).
Figure 4 compares the performance of the proposed method with that of the ML-based greedy search method. It reveals that the proposed algorithm has comparable performance to that of the ML algorithm for a balanced block with  . Figure 4(a) shows that the proposed method performs better than the ML algorithm in estimating the
. Figure 4(a) shows that the proposed method performs better than the ML algorithm in estimating the  frequency, because the proposed algorithm adjusts the sampling position to
frequency, because the proposed algorithm adjusts the sampling position to  , whereas the ML algorithm has a sample length of 56 for the estimation. The two algorithms perform similarly in this balanced block situation. However, the proposed algorithm outperforms the ML-based greedy search method in the following unbalanced block situation and in cases of random
, whereas the ML algorithm has a sample length of 56 for the estimation. The two algorithms perform similarly in this balanced block situation. However, the proposed algorithm outperforms the ML-based greedy search method in the following unbalanced block situation and in cases of random  .
.
Figure 5 presents the performance of the proposed scheme and the ML-based algorithm for a transition time close to the boundary of the data block,  . As indicated in the result, because of the lack of samples, the ML-based algorithm yields large estimation errors, revealed in Figure 5(b), while the proposed algorithm performs stably as in the case of
. As indicated in the result, because of the lack of samples, the ML-based algorithm yields large estimation errors, revealed in Figure 5(b), while the proposed algorithm performs stably as in the case of  . In particular, in Figure 5(a), the estimation error of the ML-based method is lower than the CRLB because the data length
. In particular, in Figure 5(a), the estimation error of the ML-based method is lower than the CRLB because the data length  exceeds that,
exceeds that,  , used in the CRLB.
, used in the CRLB.
In practice, transition time is a random variable for a sampling data block. The transition time  is set randomly between 1 and
is set randomly between 1 and  with a uniform distribution. As indicated in Figure 6, the performance of the proposed algorithm is similar to that with
with a uniform distribution. As indicated in Figure 6, the performance of the proposed algorithm is similar to that with  .
.
To demonstrate the tracking capability of the proposed processing scheme, the following simulation is performed with a sequence of ten frequencies. The hopping frequencies are [
 ] Hz. The complex channel gains for these frequencies are
] Hz. The complex channel gains for these frequencies are  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . The channel gains are generated using the expression
. The channel gains are generated using the expression  , where
, where  and
and  are normally distributed with zero mean and a variance of 0.05. The initial transition time
are normally distributed with zero mean and a variance of 0.05. The initial transition time  is set randomly between 1 and
is set randomly between 1 and  . As shown in Figure 7, the frequency estimation errors are less than 100 Hz over the range of the evaluation.
. As shown in Figure 7, the frequency estimation errors are less than 100 Hz over the range of the evaluation.
Figures 8(a) and 8(b) compare the experimental complexities. The CPU is Intel(R) Core(TM)2 CPU 6320 at 1.86 GHz, and the computing time of the proposed algorithm is much lower than that of the ML-based greedy search scheme. Notably, the computing time can be reduced by optimizing the program codes and designing special computer architectures for implementing the proposed scheme.
6. Conclusions
A robust blind frequency and timing estimation algorithm is developed for frequency hopping systems. The proposed scheme has a lower computational load than the ML-based greedy search algorithm. The multivariable search problem is reduced to a single variable search problem. The algorithm does not require the simultaneous search of all times and frequencies, and its performance is comparable with that of the ML-based greedy search algorithm. The problem of unbalanced situations (where  is close to the boundary) is solved using the proposed algorithm. The simulation results indicate that the performance is relatively independent of transition time
is close to the boundary) is solved using the proposed algorithm. The simulation results indicate that the performance is relatively independent of transition time  , whereas the pure ML-based algorithm fails to estimate the parameters. The proposed algorithm can be adapted for tracking. The tracking performance is also demonstrated by utilizing the estimated parameters of
, whereas the pure ML-based algorithm fails to estimate the parameters. The proposed algorithm can be adapted for tracking. The tracking performance is also demonstrated by utilizing the estimated parameters of  and
and  in the previous data block and the computational task of estimating
in the previous data block and the computational task of estimating  is omitted to reduce complexity.
is omitted to reduce complexity.
References
Zhao H, Wang Q: On frequency hop synchronization in multipath rayleigh fading. IEEE Transactions on Vehicular Technology 1998, 47(3):1049-1065. 10.1109/25.704859
Min J, Samueli H: Synchronization techniques for a frequency-hopped wireless transceiver. Proceedings of the 46th IEEE Vehicular Technology Conference, May 1996 183-187.
Min JS, Samueli H: Analysis and design of a frequency-hopped spread-spectrum transceiver for wireless personal communications. IEEE Transactions on Vehicular Technology 2000, 49(5):1719-1731. 10.1109/25.892577
Siu YM, Chan WS, Leung SW: A SFH spread spectrum synchronization algorithm for data broadcasting. IEEE Transactions on Broadcasting 2001, 47(1):71-75. 10.1109/11.920783
Qiu Y, Gan Z, Pan Y: Research on downlink synchronization of a frequency-hopping satellite communication system. Proceedings of the International Conference on Communication Technology Proceedings (ICCT '98), October 1998 1: S17051-S17054.
Li W, Wang J, Yao Y: Synchronization design of frequency-hopping communication system. Proceedings of the International Conference on Communication Technology Proceedings (ICCT '98), October 1998 1: 115-119.
Liang J, Gao L, Yang S: Frequency estimation and synchronization of frequency hopping signals based on reversible jump MCMC. Proceedings of the International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS '05), December 2005 589-592.
Liu X, Li J, Ma X: An EM algorithm for blind hop timing estimation of multiple FH signals using an array system with bandwidth mismatch. IEEE Transactions on Vehicular Technology 2007, 56(5):2545-2554.
Fan H, Guo Y, Feng X: Blind parameter estimation of frequency hopping signals based on matching pursuit. Proceedings of the 4th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM '08), October 2008
Mallat SG, Zhang Z: Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing 1993, 41(12):3397-3415. 10.1109/78.258082
Liu X, Sidiropoulos ND, Swami A: Joint hop timing and frequency estimation for collision resolution in FH networks. IEEE Transactions on Wireless Communications 2005, 4(6):3063-3073.
Valyrakis A, Tsakonas EE, Sidiropoulos ND, Swami A: Stochastic modeling and particle filtering algorithms for tracking a frequency-hopped signal. IEEE Transactions on Signal Processing 2009, 57(8):3108-3118.
Ko CC, Zhi W, Chin F: ML-based frequency estimation and synchronization of frequency hopping signals. IEEE Transactions on Signal Processing 2005, 53(2):403-410.
Ziskind I, Wax M: Maximum likelihood localization of multiple sources by alternating projection. IEEE Transactions on Acoustics, Speech, and Signal Processing 1988, 36(10):1553-1560. 10.1109/29.7543
Acknowledgment
The authors would like to thank the National Science Council of the Republic of China, Taiwan, for financially supporting this research under Contract no. NSC_99-2221-E-008 -039.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The likelihood function of the received signal is

The random sizes of the subvectors that are associated with the random parameter  make the derivation of the CRLBs for all estimates very complicated. Alternatively, if the goal is to put the received block into a balanced situation,
make the derivation of the CRLBs for all estimates very complicated. Alternatively, if the goal is to put the received block into a balanced situation,  is assumed. The
is assumed. The  -sample block is divided into two
-sample block is divided into two  -sample blocks. Hence, the likelihood function can be expressed as
-sample blocks. Hence, the likelihood function can be expressed as

The log-likelihood functions are


Equations (A.3) and (A.4) have similar forms. The CRLB that is associated with (A.3) is derived as follows. (That associated with (A.4) can be derived similarly). Differentiation of (A.3) with respect to  yields
yields

where

Further differentiating (A.5) yields

Substituting (A.7) into the Fisher information function yields

Finally, the CRLB is given by

Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fu, KC., Chen, YF. Robust Blind Frequency and Transition Time Estimation for Frequency Hopping Systems. EURASIP J. Adv. Signal Process. 2010, 172703 (2010). https://doi.org/10.1155/2010/172703
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/172703

 .
.
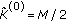 and estimate the frequencies that maximize
and estimate the frequencies that maximize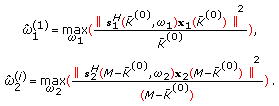
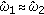 , then shift
, then shift  forward and backward, yielding two blocks,
forward and backward, yielding two blocks,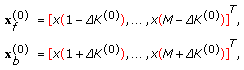
 . Then, select one of the two blocks by applying the following decision rule:
. Then, select one of the two blocks by applying the following decision rule:
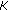 using
using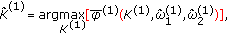

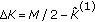
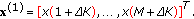
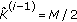 and estimate the frequencies that maximize
and estimate the frequencies that maximize
 using
using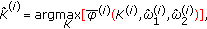
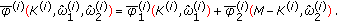
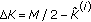



 estimate, (b) RMSE of
estimate, (b) RMSE of  estimate, (c) RMSE of K estimate, and (d) error probability of K.
estimate, (c) RMSE of K estimate, and (d) error probability of K.
 estimate, (b) RMSE of
estimate, (b) RMSE of  estimate, (c) RMSE of K estimate, and (d) error probability of K.
estimate, (c) RMSE of K estimate, and (d) error probability of K.
 . (a) RMSE of
. (a) RMSE of  estimate, (b) RMSE of
estimate, (b) RMSE of  estimate, (c) RMSE of K estimate, and (d) error probability of K.
estimate, (c) RMSE of K estimate, and (d) error probability of K.
 . (a) Frequency tracking and (b) RMSE of frequency tracking.
. (a) Frequency tracking and (b) RMSE of frequency tracking.