- Research Article
- Open access
- Published:
Optimized Paraunitary Filter Banks for Time-Frequency Channel Diagonalization
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 172751 (2010)
Abstract
We adopt the concept of channel diagonalization to time-frequency signal expansions obtained by DFT filter banks. As a generalization of the frequency domain channel representation used by conventional orthogonal frequency-division multiplexing receivers, the time-frequency domain channel diagonalization can be applied to time-variant channels and aperiodic signals. An inherent error in the case of doubly dispersive channels can be limited by choosing adequate windows underlying the filter banks. We derive a formula for the mean-squared sample error in the case of wide-sense stationary uncorrelated scattering (WSSUS) channels, which serves as objective function in the window optimization. Furthermore, an enhanced scheme for the parameterization of tight Gabor frames enables us to constrain the window in order to define paraunitary filter banks. We show that the design of windows optimized for WSSUS channels with known statistical properties can be formulated as a convex optimization problem. The performance of the resulting windows is investigated under different channel conditions, for different oversampling factors, and compared against the performance of alternative windows. Finally, a generic matched filter receiver incorporating the proposed channel diagonalization is discussed which may be essential for future reconfigurable radio systems.
1. Introduction
Motivated by the heterogeneity of today's world of wireless communications—which includes cellular mobile radio systems of the second and third generations and beyond, wireless local and personal area networks, broadband wireless access systems, digital audio and video broadcast, emerging peer-to-peer radio, and so forth—particular attention is given to reconfigurable radio architectures. Essential in this context are radio resource management solutions on the higher layers and the ability to comply with a range of different air interfaces on the physical layer. Devices comprising the logic for handling multiple air interfaces in the form of parallel implementations are widely available. However, in view of the still increasing number of standards, monolithic transceiver architectures are desirable which enable a uniform processing of different signals by means of reconfigurable multipurpose signal processing units.
A major challenge in the design of a universal baseband receiver architecture is posed by the dispersive radio channel. For dealing with signal dispersion, fundamentally different approaches are followed in traditional radios depending on the type of modulation. Receivers for single-carrier signals typically model the channel as a tapped delay line. For known coefficients of the delay line, the information in the transmitted signal can be recovered by means of a matched filtering followed by a sequence detector or using instead an equalizer followed by a simple detector. The complexity of the coefficient estimation and detection schemes increases with the delay dispersion and thus with the number of taps. Orthogonal frequency-division multiplexing (OFDM) can evade the need for complex equalizers in high data rate systems. The cyclic extensions in OFDM signals facilitate a frequency domain representation of the multipath channel in the form of parallel single-tap lines. On the basis of the frequency domain signal description resulting from the block-wise Discrete Fourier Transform (DFT), the signal mapping by multipath channels can be represented as diagonal matrices. This channel diagonalization enables straightforward demodulation and coefficient estimation and has, along with the availability of Fast Fourier Transform (FFT) algorithms, led to the popularity of OFDM.
The aforementioned approach for a simple channel inversion based on a frequency domain description is not limited to OFDM receivers. Single-carrier modulation with frequency domain equalization (FDE) can achieve similar performance as OFDM if a proper cyclic prefix is appended to each block of signals [1]. In [2] the computational complexities of time and frequency domain equalizers are compared and it is shown that FDE is simpler when the length of the stationary channel impulse response exceeds the sample time by a factor of 5 or more. Processing signals without cyclic prefix result in errors at the block boundaries. These errors have a limited impact at sufficiently large block sizes, which makes FDE an interesting alternative for code-division multiple access receivers [3, 4].
The limitations of OFDM receivers and FDE to time-invariant channels and certain signal formats can be overcome by resorting to alternative signal representations. A natural choice for the signal transform is the discrete-time Gabor expansion [5] based on a system of time-frequency (TF) shifted versions of a certain window function. Even though a TF domain channel diagonalization based on such a Gabor expansion is approximative in the general case of time-variant channels and aperiodic signals, for the typical underspread channels encountered in mobile radio scenarios the inherent model error can be limited to a usually acceptable level by choosing an adequate window underlying the signal transform [6].
The transform of discrete-time signals into the TF domain can be accomplished by DFT filter banks, for which similarly efficient FFT-based implementations are available as for plain DFTs [7]. There is plenty of literature on filter bank design in the context of generalized multicarrier/multitone modulation in wireless/wired communications. Replacing the block-wise inverse DFT and DFT in the transmitter and receiver, respectively, by more general filter banks is a way to get rid of the rigid framework of rectangular windows and cyclic prefixes in OFDM systems. Interference between adjacent sub-bands or multicarrier symbols can be avoided, or at least limited, by choosing appropriate transmit pulses. Filter banks for transmission over dispersive channels with limited interchannel and intersymbol interference are designed in [8–14].
The optimization of filter banks for specific objective functions and constraints can sometimes be formulated as a convex optimization (CO) problem [12]. In [15], CO methods are employed for the design of a two-channel multirate filter bank, in [16] for the design of pulse shapes which minimize intercarrier interference due to frequency offsets in OFDM systems, in [17] for finding optimized prototype filters for filtered multitone modulation used in digital subscriber line systems, and in [18] for the design of filter banks for sub-band signal processing under minimal aliasing and induced distortion. Semidefinite programming (SDP), a branch of CO for which efficient numerical solution methods are available, was employed in [19] for the design of a linear phase prototype filter with high stopband attenuation for cosine-modulated filter banks. In [20] two-channel filter banks are optimized under similar criteria by SDP.
In this paper we are not concerned with the design of transmit pulses. Rather, we optimize filter banks in the context of channel diagonalization. We are interested exclusively in paraunitary filter banks, which are related to the concept of tight Gabor frames [21]. The signal transform associated with discrete-time tight Gabor frames fulfills Parseval's identity. This property is crucial for flexible receivers as it lets the correlation between two time domain signals be computed based on the respective TF signal representations. A main concern of this paper is the design of tight Gabor frames facilitating TF domain channel diagonalization with minimal model error for given channel conditions. More specifically, we minimize the mean-squared error (MSE) resulting from the diagonalization of random channels with known second-order statistical properties, complying with the wide-sense stationary uncorrelated scattering (WSSUS) model, with respect to the TF window function. As we showed in [6], window functions minimizing the MSE appearing in the TF domain can be computed by SDP. In this paper we directly focus on the more relevant MSE in the time domain signal. We show that for weak assumptions on the channel statistics, the optimization problem can likewise be turned into a tractable form through semidefinite relaxation. In order to be able to constrain the windows to constitute tight frames, we extend the parameterization of tight Gabor frames presented in [22]. Optimized windows can then be computed off-line for different channel conditions encountered by reconfigurable receivers, such as the generic matched filter-based inner receiver discussed in this paper.
1.1. Outline of This Paper
In Section 2, the mathematical concepts for TF representation and processing of signals are introduced. A parameterization of tight Gabor frames, needed for the constrained optimization in Section 5 is presented in Section 3. In Section 4, TF domain channel diagonalization is discussed, resulting in a certain error in the case of doubly dispersive channels. As shown in Section 5, semidefinite relaxation lets the window design problem be formulated as a CO problem. Numerical results are shown in Section 6 for different channel conditions. In Section 7, a generic matched filter architecture incorporating the channel diagonalization is presented. Finally, conclusions are drawn in Section 8.
1.2. Notation
We enclose the arguments of functions defined on a discrete domain  in square brackets in order to distinguish them from functions defined on
in square brackets in order to distinguish them from functions defined on  . The Hilbert space of the square summable functions
. The Hilbert space of the square summable functions  is denoted as
is denoted as  , and the associated inner product
, and the associated inner product  and
and  -norm
-norm  are given by
are given by  and
and  , respectively, where the asterisk in the superscript denotes complex conjugation. Furthermore, we use
, respectively, where the asterisk in the superscript denotes complex conjugation. Furthermore, we use  to denote convolution, and
to denote convolution, and  for the one-by-one multiplication of two compatible functions
for the one-by-one multiplication of two compatible functions  and
and  , that is,
, that is,  corresponds to
corresponds to  for all
for all  . Vectors and matrices are denoted by boldface characters. The transpose and Hermitian transpose of a matrix
. Vectors and matrices are denoted by boldface characters. The transpose and Hermitian transpose of a matrix  are denoted as
are denoted as  and
and  , respectively,
, respectively,  stands for the paraconjugate of a polynomial matrix
stands for the paraconjugate of a polynomial matrix  (
( is obtained from
is obtained from  by transposing it, conjugating all of the coefficients of the rational functions in
by transposing it, conjugating all of the coefficients of the rational functions in  , and replacing
, and replacing  by
by  [7].),
[7].),  for the trace, and
for the trace, and  denotes the identity matrix of size
denotes the identity matrix of size  . The
. The  th element of the
th element of the  th row of a matrix
th row of a matrix  is represented as
is represented as  . Also,
. Also,  denotes the expected value,
denotes the expected value,  and
and  represent the real and imaginary parts, respectively, of complex arguments,
represent the real and imaginary parts, respectively, of complex arguments,  the modulo operation,
the modulo operation,  , and
, and  .
.
2. DFT Filter Banks and Discrete-Time Gabor Frames
In this section, we introduce signal representation concepts needed subsequently. Some important properties of discrete-time Gabor frames are recapitulated with an emphasis on tight frames and the relationship to DFT filter banks. For more insight into Gabor analysis and filter bank theory the reader is referred to the rich literature, for instance [7, 23–26].
Let  and
and  be two positive integer constants and
be two positive integer constants and  . Given a window function
. Given a window function  , the set
, the set

with

is referred to as a Gabor system in  . The elements of the Gabor system can be associated with the grid points
. The elements of the Gabor system can be associated with the grid points  of a lattice overlaying the TF plane
of a lattice overlaying the TF plane  . If there exist two positive constants
. If there exist two positive constants  and
and  such that
such that

then (1) represents a discrete-time Gabor frame. A necessary condition for (3) is that  .
.
For an arbitrary signal  the inner products of
the inner products of  with every element of the system (1) form a linear TF representation. In the following, the corresponding transform onto
with every element of the system (1) form a linear TF representation. In the following, the corresponding transform onto  is represented by the analysis operator
is represented by the analysis operator

The mapping (4) can be implemented by a  -channel DFT (analysis) filter bank with a prototype filter with impulse response
-channel DFT (analysis) filter bank with a prototype filter with impulse response  followed by a down-sampling by a factor
followed by a down-sampling by a factor  [21]. Conversely, a synthesis operator
[21]. Conversely, a synthesis operator  can be defined based on (1) which maps an arbitrary TF representation
can be defined based on (1) which maps an arbitrary TF representation  onto an element of
onto an element of  according to
according to

The signal synthesis (5) can be implemented by an up-sampling by a factor  followed by a
followed by a  -channel DFT (synthesis) filter bank with a prototype filter with impulse response
-channel DFT (synthesis) filter bank with a prototype filter with impulse response  .
.
If (3) holds with  then (1) represents a (normalized) tight Gabor frame and
then (1) represents a (normalized) tight Gabor frame and  for all
for all  . These special Gabor frames obey a generalized Parseval's identity
. These special Gabor frames obey a generalized Parseval's identity

Furthermore, the inner product  of any two
of any two  can be computed on the basis of the respective TF representations
can be computed on the basis of the respective TF representations  and
and  , that is,
, that is,

Henceforth we assume that (1) represents a tight Gabor frame. We note that the range  of the operator
of the operator  is a subspace of
is a subspace of  , and the mapping
, and the mapping  is an isometry. If
is an isometry. If  the operator
the operator  represents the orthogonal projection from
represents the orthogonal projection from  onto
onto  . As a direct consequence,
. As a direct consequence,

and  .
.
Tight Gabor frames are associated with paraunitary DFT filter banks. To enable the design of windows with favorable properties, for instance in regard to TF concentration, it is often necessary to indeed choose  , resulting in oversampled filter banks. Besides of available efficient implementations of paraunitary DFT filter banks, the properties (6) and (7) are of prime interest for reconfigurable baseband receivers since they allow operations for the signal demodulation, such as signal energy computations and crosscorrelations with reference waveforms, to be performed directly in the TF domain.
, resulting in oversampled filter banks. Besides of available efficient implementations of paraunitary DFT filter banks, the properties (6) and (7) are of prime interest for reconfigurable baseband receivers since they allow operations for the signal demodulation, such as signal energy computations and crosscorrelations with reference waveforms, to be performed directly in the TF domain.
3. Parameterization of Tight Gabor Frames
The conditions under which (1) represents a tight Gabor frame can be formulated via the polyphase representation. Let  denote the least common multiple of
denote the least common multiple of  and
and  , and define
, and define  and
and  such that
such that  and
and  . The
. The  -component polyphase representation of the
-component polyphase representation of the  -transform
-transform  of the window
of the window  reads
reads

where

Furthermore, the polyphase matrix  of size
of size  associated with the DFT filter bank implementing (4) can be expressed as [22]
associated with the DFT filter bank implementing (4) can be expressed as [22]

with  denoting the DFT matrix of size
denoting the DFT matrix of size  (defined as
(defined as  ) and
) and

Here,  is the diagonal matrix with diagonal elements
is the diagonal matrix with diagonal elements  . The Gabor system (1) represents a tight frame in
. The Gabor system (1) represents a tight frame in  if and only if the polyphase matrix
if and only if the polyphase matrix  is paraunitary with
is paraunitary with  . Or, equivalently, if and only if the polynomial matrix
. Or, equivalently, if and only if the polynomial matrix  is paraunitary with
is paraunitary with  , since
, since  .
.
We observe that  if
if  , where
, where  . Consequently,
. Consequently,  is paraunitary if and only if the
is paraunitary if and only if the  matrices
matrices  of size
of size  , which comprise the possibly nonzero elements of
, which comprise the possibly nonzero elements of  according to
according to  , are all paraunitary. As follows from (12) the elements of the
, are all paraunitary. As follows from (12) the elements of the  matrices are given as
matrices are given as

with  and
and  denoting the Kronecker delta.
denoting the Kronecker delta.
Note that if the sequences  were identical for all column indices
were identical for all column indices  except for differing offsets, then the factor
except for differing offsets, then the factor  could be omitted in (13) without affecting the condition
could be omitted in (13) without affecting the condition  . Replacing some
. Replacing some  by the equivalent
by the equivalent  is a way to align the sequences. Having this in mind, we define
is a way to align the sequences. Having this in mind, we define  matrices
matrices  of size
of size  according to
according to

with the index map

Since the polynomial matrices  are paraunitary if and only if the modified matrices
are paraunitary if and only if the modified matrices  are paraunitary, the Gabor system (1) represents a tight frame in
are paraunitary, the Gabor system (1) represents a tight frame in  if and only if
if and only if

We note that the size of each polynomial matrix  , their number
, their number  , and the index map
, and the index map  are fully determined by
are fully determined by  and
and  . Given the latter two constants, any tight Gabor frame is uniquely defined by an instance of
. Given the latter two constants, any tight Gabor frame is uniquely defined by an instance of  satisfying (16), where the association of the elements of the
satisfying (16), where the association of the elements of the  matrices with the samples of the window
matrices with the samples of the window  is defined by (14) and (10). The length of the window is related to the polynomial orders of the matrices
is defined by (14) and (10). The length of the window is related to the polynomial orders of the matrices  . We define
. We define  as the maximal polynomial order of the
as the maximal polynomial order of the  matrices plus
matrices plus  . Thus, in the case
. Thus, in the case  , all elements of the matrices are scalars, and the support of the representable functions
, all elements of the matrices are scalars, and the support of the representable functions  is limited to
is limited to  . This set is usually not of the form
. This set is usually not of the form  for some
for some  but exhibits "gaps" as illustrated in the example of Figure 1. By increasing
but exhibits "gaps" as illustrated in the example of Figure 1. By increasing  longer windows can be found.
longer windows can be found.
4. Time-Frequency Channel Diagonalization
The mapping  of an input signal
of an input signal  onto the signal
onto the signal  at the output of a linear time-variant channel can be expressed as
at the output of a linear time-variant channel can be expressed as

where  denotes the time-variant impulse response. We consider random channels where
denotes the time-variant impulse response. We consider random channels where  represents a two-dimensional zero-mean random process complying with the WSSUS model. The second-order statistics of
represents a two-dimensional zero-mean random process complying with the WSSUS model. The second-order statistics of  are determined by the time correlation function
are determined by the time correlation function  and the delay power spectrum
and the delay power spectrum  according to
according to

The delay power spectrum is related to the frequency correlation function  through
through

Of interest in the context of TF signal processing is the time-variant transfer function

reflecting the TF selectivity of a channel realization. In a digital receiver a realization of a doubly dispersive channel can be represented by a sampled version  of
of  , defined by
, defined by

For compatibility with the TF signal representations introduced in Section 2, the sampling intervals  and
and  are chosen in line with those for the Gabor system (1). The time-variant transfer function represents the complex-valued channel gain over time and frequency. Hence, given the TF representation
are chosen in line with those for the Gabor system (1). The time-variant transfer function represents the complex-valued channel gain over time and frequency. Hence, given the TF representation  of a signal
of a signal  at the channel input, it is straightforward to approximate the signal
at the channel input, it is straightforward to approximate the signal  at the channel output as
at the channel output as

The approximation of a linear operator by  , that is, a concatenation of an analysis operation, an element-wise multiplication, and a synthesis operation, appears in the literature under the name Gabor multiplier [27]. Such an approximation is suitable for operators that do not involve TF shifts of large magnitude (i.e., underspread operators). Figure 2 shows an implementation of (22) by filter banks, where
, that is, a concatenation of an analysis operation, an element-wise multiplication, and a synthesis operation, appears in the literature under the name Gabor multiplier [27]. Such an approximation is suitable for operators that do not involve TF shifts of large magnitude (i.e., underspread operators). Figure 2 shows an implementation of (22) by filter banks, where  denotes the
denotes the  -transform of
-transform of  . The TF channel diagonalization offers several advantages. The flexibility in the choice of the sampling intervals
. The TF channel diagonalization offers several advantages. The flexibility in the choice of the sampling intervals  and
and  can be used for the adaptation to different channel conditions or signal formats, or the limitation of the effort for the coefficient estimation in certain receivers. Furthermore, the channel diagonalization facilitates scalable and efficient receiver processing known from OFDM.
can be used for the adaptation to different channel conditions or signal formats, or the limitation of the effort for the coefficient estimation in certain receivers. Furthermore, the channel diagonalization facilitates scalable and efficient receiver processing known from OFDM.
As a result of the sampling of  the model (22) is usually only approximative, and
the model (22) is usually only approximative, and  is an approximation of the channel output. The accuracy of
is an approximation of the channel output. The accuracy of  depends on the channel characteristics and the underlying Gabor frame. We may expect the model error to be limited if every elementary function
depends on the channel characteristics and the underlying Gabor frame. We may expect the model error to be limited if every elementary function  is concentrated around
is concentrated around  in the TF plane such that
in the TF plane such that  is essentially constant within the sphere of
is essentially constant within the sphere of  . Window functions fulfilling this can be designed for the typical underspread channels encountered in mobile radio scenarios by CO, as shown in Section 5.
. Window functions fulfilling this can be designed for the typical underspread channels encountered in mobile radio scenarios by CO, as shown in Section 5.
The error from the channel diagonalization is given by

In order to remain general in regard to signal and channel properties, we consider the error signal under the assumptions of
-
(i)
a white random signal at the channel input,
-
(ii)
a random channel
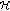 complying with the WSSUS model and unit average channel gain (i.e.,
complying with the WSSUS model and unit average channel gain (i.e., 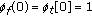 ).
).
To formulate the resulting MSE, we introduce the random signal  being subject to
being subject to  and
and

with  an even integer. The error signal corresponding to the truncated white random input signal
an even integer. The error signal corresponding to the truncated white random input signal  reads
reads

The error signal sample energy relative to the unit average sample energy of the desired signal, in the following termed relative mean-squared sample error (RMSSE), can be expressed as

Making use of the above assumptions, the RMSSE can be written as

as shown in the appendix. Having formulated both conditions for the window  to define a tight Gabor frame (in Section 3) and the error resulting from the channel diagonalization based on
to define a tight Gabor frame (in Section 3) and the error resulting from the channel diagonalization based on  , we can now turn to window optimization.
, we can now turn to window optimization.
5. Window Design
Let us represent the window to be optimized in vector form  , choosing
, choosing  such that
such that  comprises the support of
comprises the support of  expressed in Section 3. We consider only real-valued windows. Additionally, in order to eventually arrive at a CO problem, we impose the following restrictions on the channel statistics.
expressed in Section 3. We consider only real-valued windows. Additionally, in order to eventually arrive at a CO problem, we impose the following restrictions on the channel statistics.
-
(i)
The time correlation function is subject to
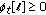 for all
for all  , as being the case for two-sided exponentially decaying and many other symmetrical Doppler power spectra.
, as being the case for two-sided exponentially decaying and many other symmetrical Doppler power spectra. -
(ii)
The frequency correlation function fulfills
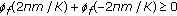 for all
for all  , as, for instance, in the case of exponentially decaying delay power spectra.
, as, for instance, in the case of exponentially decaying delay power spectra.
We note that  can be expressed as
can be expressed as  and
and  as
as  with appropriate square matrices
with appropriate square matrices  and
and  . As a consequence, the objective function (27) can be expressed in the form
. As a consequence, the objective function (27) can be expressed in the form

for some  depending on the support of
depending on the support of  , where
, where  are real matrices and the constants
are real matrices and the constants  are positive given the above restrictions.
are positive given the above restrictions.
Next, we need to incorporate the constraints under which  will be minimized. In order to formulate the constraints (16) on the window in the time domain, it is helpful to permute the samples in
will be minimized. In order to formulate the constraints (16) on the window in the time domain, it is helpful to permute the samples in  . Let us introduce a window
. Let us introduce a window  of length
of length  defined as
defined as

with  ,
,  ,
,  , and
, and  . The matrices
. The matrices  and the samples of the permuted window are related through
and the samples of the permuted window are related through

With (30) we can now translate the polyphase domain constraints (16) into constraints on the permuted window defined by  .
.
( ) Case
) Case  . There are
. There are  constraints of form
constraints of form  . The
. The  th diagonal matrix
th diagonal matrix  of size
of size  is defined as
is defined as

with  . Additionally, there are
. Additionally, there are  constraints of form
constraints of form  . The corresponding matrices
. The corresponding matrices 
 can be defined as the elements of the set resulting from deleting duplicate elements and zero-matrices from
can be defined as the elements of the set resulting from deleting duplicate elements and zero-matrices from

where in (32) we let  equal zero if either
equal zero if either  or
or  .
.
( ) Case
) Case  . From each of the above-defined matrices
. From each of the above-defined matrices  ,
,  unique block diagonal matrices of dimension
unique block diagonal matrices of dimension  are reproduced which contain the original matrix as one of the
are reproduced which contain the original matrix as one of the  diagonal blocks of dimension
diagonal blocks of dimension  . Hence, there are
. Hence, there are  constraints in total. The constraint matrices are mutually orthogonal in the sense that
constraints in total. The constraint matrices are mutually orthogonal in the sense that  for
for  .
.
We can now formulate the optimization problem in the form

where  are the matrices resulting from
are the matrices resulting from  by permuting the rows and columns in accordance with (29), and
by permuting the rows and columns in accordance with (29), and  . This problem is difficult to tackle for large
. This problem is difficult to tackle for large  . Let us thus introduce
. Let us thus introduce  and reformulate the optimization problem as
and reformulate the optimization problem as

where  denotes the vector space of symmetric matrices of dimension
denotes the vector space of symmetric matrices of dimension  . In (34) we have a convex objective function, however, the set
. In (34) we have a convex objective function, however, the set  is nonconvex. Resorting to semidefinite relaxation, we obtain
is nonconvex. Resorting to semidefinite relaxation, we obtain

with  denoting that
denoting that  is positive semidefinite. Since
is positive semidefinite. Since  is a convex subset of
is a convex subset of  , we now have a CO problem [28]. Having found a matrix
, we now have a CO problem [28]. Having found a matrix  corresponding to a global minimum of (35), we have two possible cases. If
corresponding to a global minimum of (35), we have two possible cases. If  , a solution
, a solution  of (33) is readily obtainable from
of (33) is readily obtainable from  and the optimal window
and the optimal window  is found through (29). If
is found through (29). If  , which we observe in most of the cases, rank reduction methods must be employed. We compute a possibly suboptimal window
, which we observe in most of the cases, rank reduction methods must be employed. We compute a possibly suboptimal window  by the following three steps.
by the following three steps.
-
(i)
In order to reduce the rank to
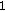 , we resort to the matrix
, we resort to the matrix  composed by the dominant eigenvector
composed by the dominant eigenvector  of
of 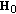 , since
, since 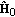 is the matrix nearest to
is the matrix nearest to  in terms of the Frobenius norm [29].
in terms of the Frobenius norm [29]. -
(ii)
We translate
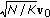 into a window
into a window 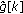 taking the sample permutation defined in (29) into account.
taking the sample permutation defined in (29) into account. -
(iii)
We finally obtain
 by the algorithm [30], which yields a window defining a tight frame and at the same time minimizes the distance to a given window (i.e.,
by the algorithm [30], which yields a window defining a tight frame and at the same time minimizes the distance to a given window (i.e., 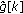 ) in terms of the
) in terms of the  -norm.
-norm.
Employing steepest descent methods for solving (35) may result in very slow convergence, whereas alternative methods may not be applicable when the number of dimensions is large. Neglecting the quadratic terms in the objective function leads to the simplified optimization problem

As shown in [6], the linear objective function  reflects the mean-squared deviation of
reflects the mean-squared deviation of  from
from  , that is, the model error in the TF domain. Problems of the form (36) are dealt with by SDP, a subfield of CO. For the efficient solution of these optimization problems a number of sophisticated software packages are widely available. However, because generally
, that is, the model error in the TF domain. Problems of the form (36) are dealt with by SDP, a subfield of CO. For the efficient solution of these optimization problems a number of sophisticated software packages are widely available. However, because generally  the windows resulting from solving (36) do not minimize the time domain error signal, the magnitude of which determines the performance of the channel diagonalization.
the windows resulting from solving (36) do not minimize the time domain error signal, the magnitude of which determines the performance of the channel diagonalization.
6. Numerical Results
We consider a WSSUS channel with an exponentially decaying delay power spectrum, the sampled version of which reads

with  denoting the unit step function and
denoting the unit step function and  the root mean-squared (RMS) delay spread [31]. As for the Doppler power spectrum, a two-sided exponentially decaying shape is assumed, which results in the time correlation function
the root mean-squared (RMS) delay spread [31]. As for the Doppler power spectrum, a two-sided exponentially decaying shape is assumed, which results in the time correlation function

where  represents the RMS Doppler spread. Since choosing an oversampling factor
represents the RMS Doppler spread. Since choosing an oversampling factor  larger than one increases the degrees of freedom in the window design, we restrict our attention to scenarios with
larger than one increases the degrees of freedom in the window design, we restrict our attention to scenarios with  , involving oversampled filter banks. Figure 3 shows optimized window functions for different channel conditions and their Fourier transforms. The waveforms were obtained numerically by solving (35) using interior point methods [28] for
, involving oversampled filter banks. Figure 3 shows optimized window functions for different channel conditions and their Fourier transforms. The waveforms were obtained numerically by solving (35) using interior point methods [28] for  ,
,  ,
,  amounting to a window length of 240 samples. An RMS delay spread
amounting to a window length of 240 samples. An RMS delay spread  of
of  samples and an RMS Doppler spread
samples and an RMS Doppler spread  of 0.001
of 0.001  were assumed in Figure 3(a), while
were assumed in Figure 3(a), while  ,
,  in Figure 3(b). The two shown optimized windows achieve RMSSEs (27) of
in Figure 3(b). The two shown optimized windows achieve RMSSEs (27) of  dB and
dB and  dB. Figures 3(c) and 3(d) show the Fourier transforms of the optimized pulses in (a) and (b), respectively, versus the normalized frequency
dB. Figures 3(c) and 3(d) show the Fourier transforms of the optimized pulses in (a) and (b), respectively, versus the normalized frequency  . Obviously, the optimized waveforms become more concentrated in time domain as the Doppler spread increases (see Figure 3(b) versus Figure 3(a)). For increasing Doppler spreads the coherence time of the channel decreases, and the temporal support of the optimized window is reduced in order to limit the RMSSE.
. Obviously, the optimized waveforms become more concentrated in time domain as the Doppler spread increases (see Figure 3(b) versus Figure 3(a)). For increasing Doppler spreads the coherence time of the channel decreases, and the temporal support of the optimized window is reduced in order to limit the RMSSE.
The RMSSEs (27) achievable by optimized windows are shown in Figure 4 for the same lattice constants and similar types of delay/Doppler power spectra. The RMS delay spread  ranges between 0.5 and 8 samples while the RMS Doppler spread
ranges between 0.5 and 8 samples while the RMS Doppler spread  equals 0.01 sample
equals 0.01 sample . For every considered
. For every considered  a window
a window  was obtained by numerically solving the CO problem (35), and a window
was obtained by numerically solving the CO problem (35), and a window  by solving (36) through SDP, where both approaches required the above-mentioned additional steps for rank reduction. The global minimum of the objective function in (35) at
by solving (36) through SDP, where both approaches required the above-mentioned additional steps for rank reduction. The global minimum of the objective function in (35) at  , that is prior to the rank reduction, serves as a lower bound in the figure. The offsets of
, that is prior to the rank reduction, serves as a lower bound in the figure. The offsets of  and
and  from the lower bound reflect the impact of the rank reduction. Additionally, the figure shows the RMSSEs resulting from choosing a window
from the lower bound reflect the impact of the rank reduction. Additionally, the figure shows the RMSSEs resulting from choosing a window  with a root-raised-cosine (RRC) shaped magnitude spectrum with width
with a root-raised-cosine (RRC) shaped magnitude spectrum with width  and roll-off factor
and roll-off factor  . We choose this window function for comparison because it does constitute a tight Gabor frame while exhibiting superior TF localization properties compared to rectangularly shaped windows for instance. Finally, for the verification of
. We choose this window function for comparison because it does constitute a tight Gabor frame while exhibiting superior TF localization properties compared to rectangularly shaped windows for instance. Finally, for the verification of  the signals
the signals  and
and  were also obtained by simulations involving filter banks based on the optimized windows
were also obtained by simulations involving filter banks based on the optimized windows  and random signal and WSSUS channel generators, and the resulting error signal analyzed.
and random signal and WSSUS channel generators, and the resulting error signal analyzed.
Obviously, solving (35) leads to better windows than solving (36). The considerable offset of the RMSSEs from the lower bound for smaller  indicates that here the rank reduction has a significant impact on the windows. We observe that rank reduction generally has a limited effect when the delay and Doppler spreads are of similar extent, that is, when in the TF plane the delay spread relative to the sampling interval in time (i.e.,
indicates that here the rank reduction has a significant impact on the windows. We observe that rank reduction generally has a limited effect when the delay and Doppler spreads are of similar extent, that is, when in the TF plane the delay spread relative to the sampling interval in time (i.e.,  ) is of the same order of magnitude as the Doppler spread relative to the sampling interval in frequency (i.e.,
) is of the same order of magnitude as the Doppler spread relative to the sampling interval in frequency (i.e.,  ).
).
The relatively high RMSSEs found in Figure 4 are a result of the product  being in the order of
being in the order of  , a much larger value than encountered in typical mobile radio scenarios. In environments with such severe dispersion in both time and frequency, the model error performance can actually be improved by increasing the oversampling factor
, a much larger value than encountered in typical mobile radio scenarios. In environments with such severe dispersion in both time and frequency, the model error performance can actually be improved by increasing the oversampling factor  . This can be seen in Table 1, showing some
. This can be seen in Table 1, showing some  observed under the same conditions as above except for choosing different lattice constants. An RMS delay spread of
observed under the same conditions as above except for choosing different lattice constants. An RMS delay spread of  sample is assumed here. The performance clearly improves with the oversampling factor.
sample is assumed here. The performance clearly improves with the oversampling factor.
7. Generic Matched Filter Receiver
The considered TF channel diagonalization does not rely on a particular signal format, making it suitable for application in multimode receivers [32]. The burst structures defined in the various standards for wireless communications differ substantially. However, commonly the bursts incorporate preamble signals for the channel estimation along with information-bearing signals which are usually subject to a linear modulation scheme. The transmitted baseband signals generally follow the form  with
with  representing
representing  elementary waveforms, possibly complex exponentials such as in the case of OFDM, or pseudo-noise sequences as in the case of direct-sequence spread-spectrum systems. For performing channel estimation and information recovery the receiver needs to estimate the signals
elementary waveforms, possibly complex exponentials such as in the case of OFDM, or pseudo-noise sequences as in the case of direct-sequence spread-spectrum systems. For performing channel estimation and information recovery the receiver needs to estimate the signals  on the basis of the known waveforms
on the basis of the known waveforms  . To this end, the inner receiver correlates the received signal
. To this end, the inner receiver correlates the received signal  with the elementary signals as appearing at the channel output, resulting in
with the elementary signals as appearing at the channel output, resulting in

For example, in the case of signal decoding in the presence of additive white Gaussian noise,  represent a sufficient statistic. In other situations, such as for the channel parameter estimation (Efficient parameter estimators which are applicable in the context of filter bank-based multicarrier transmission are presented in [33].),
represent a sufficient statistic. In other situations, such as for the channel parameter estimation (Efficient parameter estimators which are applicable in the context of filter bank-based multicarrier transmission are presented in [33].),  is unknown.
is unknown.
The generic matched filter sketched in Figure 5 aims to compute  in the TF domain. The TF representation
in the TF domain. The TF representation  of the received signal
of the received signal  is obtained from an analysis filter bank, while TF representations
is obtained from an analysis filter bank, while TF representations  of the elementary waveforms are provided by a local repository [32]. These are mapped to the TF representations
of the elementary waveforms are provided by a local repository [32]. These are mapped to the TF representations  of
of  by means of the channel diagonalization (22) discussed in Section 4. Finally, taking advantage of Parseval's identity,
by means of the channel diagonalization (22) discussed in Section 4. Finally, taking advantage of Parseval's identity,  is computed for
is computed for  .
.
The impact of the TF channel diagonalization on the  th matched filter output can be formulated as
th matched filter output can be formulated as




where for obtaining expression (41) we exploit that  while
while  represents the orthogonal projection from
represents the orthogonal projection from  onto
onto  . The error signal
. The error signal  is in line with the error signal definition (25). Under the assumptions that the relation between
is in line with the error signal definition (25). Under the assumptions that the relation between  and
and  found in Section 4 carries over to the relation between
found in Section 4 carries over to the relation between  and
and  , and that
, and that  represents a random signal with
represents a random signal with  and
and  , the RMSSE
, the RMSSE  determines the signal-to-noise ratio
determines the signal-to-noise ratio  at the matched filter output. Since the pulse
at the matched filter output. Since the pulse  is typically a component of
is typically a component of  , the aforementioned assumptions, however, do not hold in general. Nevertheless,
, the aforementioned assumptions, however, do not hold in general. Nevertheless,  may in practice serve as a rough characterization of the performance of the matched filter in Figure 5. The performance of the TF domain matched filtering in a reconfigurable receiver architecture configured to the reception of direct-sequence spread-spectrum signals is studied in [32].
may in practice serve as a rough characterization of the performance of the matched filter in Figure 5. The performance of the TF domain matched filtering in a reconfigurable receiver architecture configured to the reception of direct-sequence spread-spectrum signals is studied in [32].
8. Conclusions
We have derived paraunitary filter banks facilitating diagonalization of doubly dispersive channels at limited inherent MSE. Making use of a suitable parameterization of tight frames, we have shown that the optimization of paraunitary DFT filter banks for given channel statistics and oversampling factors can be formulated as a CO problem. An investigation of the MSE performance achieved by the optimized windows shows that the windows obtained by CO are more favorable than conventional windows with an RRC spectrum. However, in certain configurations the necessary rank reduction following the CO has a significant impact on the window shapes. The induced potential degradation of the MSE performance may be evaded by choosing appropriate lattice constants  and
and  , specifying the down-sampling factor and the number of sub-bands, respectively, or by alternative rank reduction procedures which are yet to be devised. In general, the MSE performance can be improved at the cost of a higher complexity in terms of numbers of coefficients by increasing the oversampling factor.
, specifying the down-sampling factor and the number of sub-bands, respectively, or by alternative rank reduction procedures which are yet to be devised. In general, the MSE performance can be improved at the cost of a higher complexity in terms of numbers of coefficients by increasing the oversampling factor.
In this paper our main concern was mathematical techniques for designing optimized filter banks in the context of channel diagonalization. Reconfigurable radios are clearly a prospective field of application. Since tight frames are natural generalizations of orthonormal bases used for the signal transform in OFDM receivers, the efficient handling of dispersive channels in OFDM can be inherited by receivers not limited to signals with cyclic extensions. Flexible radio architectures which incorporate the channel diagonalization considered in this paper have been investigated within the IST project URANUS (Universal RAdio-link platform for effieNt User-centric accesS) [34]. In this project the performance of such flexible receiver architectures has been studied in the context of different air interfaces and on different levels, from the inner receiver performance with perfect and imperfect channel estimation to the link level performance. While channel diagonalization by means of properly designed filter banks has been shown to have a great potential, there are a number of related issues that need to be addressed on the way to practical solutions, such as adequate channel estimation methods, synchronization, radio resource management, and others. A comparison of the performance of flexible receivers taking advantage of the channel diagonalization as compared to conventional receiver architectures has therefore been out of the scope of this paper.
References
Sari H, Karam G, Jeanclaude I: Frequency-domain equalization of mobile radio and terrestrial broadcast channels. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '94), November 1994, San Francisco, Calif, USA 1-5.
Falconer D, Ariyavisitakul SL, Benyamin-Seeyar A, Eidson B: Frequency domain equalization for single-carrier broadband wireless systems. IEEE Communications Magazine 2002, 40(4):58-66. 10.1109/35.995852
Martoyo I: Frequency domain equalization in CDMA detection, Ph.D. thesis. Institut für Nachrichtentechnik, University of Karlsruhe; 1995.
Adachi F, Nakajima A, Takeda K, et al.: Frequency-domain equalisation for block CDMA transmission. European Transactions on Telecommunications 2008, 19(5):553-560. 10.1002/ett.1305
Bölcskei H, Hlawatsch F: Discrete zak transforms polyphase transforms and applications. IEEE Transactions on Signal Processing 1997, 45(4):851-866. 10.1109/78.564174
Ju Z, Hunziker T, Dahlhaus D: Time-frequency parameterization of doubly dispersive channels. Proceedings of the European Signal Processing Conference (EUSIPCO '09), August 2009, Glasgow, UK
Vaidyanathan PP: Multirate Systems and Filter Banks. Prentice-Hall, Englewood Cliffs, NJ, USA; 1993.
Jung P, Wunder G: The WSSUS pulse design problem in multicarrier transmission. IEEE Transactions on Communications 2007, 55(10):1918-1928.
Phoong S-M, Chang Y, Chen C-Y: DFT-modulated filterbank transceivers for multipath fading channels. IEEE Transactions on Signal Processing 2005, 53(1):182-192.
Jung P, Wunder G: Iterative pulse shaping for Gabor signaling in WSSUS channels. Proceedings of IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '04), 2004, Lisbon, Portugal 368-372.
Schniter P: A new approach to multicarrier pulse design for doubly-dispersive channels. Proceedings of the Allerton Conference on Communication, Control, and Computing, October 2003, Monticello, Ill, USA
Strohmer T, Beaver S: Optimal OFDM design for time-frequency dispersive channels. IEEE Transactions on Communications 2003, 51(7):1111-1122. 10.1109/TCOMM.2003.814200
Bellanger MG: Specification and design of a prototype filter for filter bank based multicarrier transmission. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '01), 2001 4: 2417-2420.
Kozek W, Molisch AF: Nonorthogonal pulseshapes for multicarrier communications in doubly dispersive channels. IEEE Journal on Selected Areas in Communications 1998, 16(8):1579-1589. 10.1109/49.730463
Houwen S, Chen T, Norman SA: Design of FIR multirate filter banks using convex optimization. Proceedings of IEEE Pacific RIM Conference on Communications, Computers, and Signal Processing, August 1997, Victoria, Canada 1: 469-472.
Xu J, Strohmer T: Pulse construction in OFDM systems via convex optimization. IEEE Transactions on Communications 2008, 56(8):1225-1230.
Borna B, Davidson TN: Efficient filter bank design for filtered multitone modulation. Proceedings of IEEE International Conference on Communications, June 2004, Paris, France 1: 38-42.
Wilbur MR, Davidson TN, Reilly JP: Efficient design of oversampled NPR GDFT filterbanks. IEEE Transactions on Signal Processing 2004, 52(7):1947-1963. 10.1109/TSP.2004.828936
Kha HH, Tuan HD, Nguyen TQ: Efficient design of cosine-modulated filter banks via convex optimization. IEEE Transactions on Signal Processing 2009, 57(3):966-976.
Karmakar A, Kumar A, Patney RK: Design of an optimal two-channel orthogonal filterbank using semidefinite programming. IEEE Signal Processing Letters 2007, 14(10):692-694.
Bölcskei H, Hlawatsch F, Feichtinger HG: Equivalence of DFT filter banks and Gabor expansions. Wavelet Applications in Signal and Image Processing III, July 1995, San Diego, Calif, USA, Proceedings of SPIE 2569: 128-139.
Cvetkovic Z, Vetterli M:Tight Weyl-Heisenberg frames in
 . IEEE Transactions on Signal Processing 1998, 46(5):1256-1259. 10.1109/78.668789
. IEEE Transactions on Signal Processing 1998, 46(5):1256-1259. 10.1109/78.668789Feichtinger HG, Strohmer T: Gabor Analysis and Algorithms: Theory and Applications. Birkhäuser, Boston, Mass, USA; 1998.
Gröchenig K: Foundations of Time-Frequency Analysis. Birkhäuser, Boston, Mass, USA; 2001.
Kovačević J, Chebira A: Life beyond bases: the advent of frames (Part I). IEEE Signal Processing Magazine 2007, 24(4):86-104.
Kovačević J, Chebira A: Life beyond bases: the advent of frames (Part II). IEEE Signal Processing Magazine 2007, 24(5):115-125.
Feichtinger HG, Hampejs M, Kracher G: Approximation of matrices by Gabor multipliers. IEEE Signal Processing Letters 2004, 11(11):883-886. 10.1109/LSP.2004.833581
Boyd S, Vandenberghe L: Convex Optimization. Cambridge University Press, Cambridge, UK; 2004.
Golub GH, Loan CFV: Matrix Computations. 3rd edition. Johns Hopkins University Press, Baltimore, Md, USA; 1996.
Janssen AJEM, Søndergaard PL: Iterative algorithms to approximate canonical Gabor windows: computational aspects. Journal of Fourier Analysis and Applications 2007, 13(2):211-241. 10.1007/s00041-006-6069-y
Bello PA: Characterization of randomly time-variant linear channels. IEEE Transactions on Communications Systems 1963, 11: 360-393. 10.1109/TCOM.1963.1088793
Hunziker T, Ju Z, Dahlhaus D: A reconfigurable baseband receiver architecture based on time-frequency signal processing. Proceedings of the ICT Mobile and Wireless Communications Summit, June 2009, Santander, Spain
Hunziker T, Stefanatos S: Efficient two-dimensional filters for doubly-dispersive channel estimation in time-frequency signal processing. Proceedings of the 10th IEEE International Symposium on Spread Spectrum Techniques and Applications (ISSSTA '08), August 2008, Bologna, Italy 381-385.
European research project IST-27960, URANUS (Universal RAdio-link platform for efficieNt User-centric accesS), http://www.ist-uranus.org/
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
A. Derivation of RMSSE Formula
The RMSSE can be written as

where

and

Both the input signal power and the gain of the channel are normalized to unity, and therefore  .
.
Furthermore,  can be expressed as
can be expressed as



where  . To obtain (A.5) from (A.4) we apply (21), (20), and (24), and to arrive at (A.6) we use (18). Using (2) and (19),
. To obtain (A.5) from (A.4) we apply (21), (20), and (24), and to arrive at (A.6) we use (18). Using (2) and (19),  can now be expressed as
can now be expressed as

Finally  can be rewritten as
can be rewritten as





We use (24) to obtain (A.9) from (A.8), and for the derivation of (A.10), (18) is applied. Thus, the RMSSE is given by

Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ju, Z., Hunziker, T. & Dahlhaus, D. Optimized Paraunitary Filter Banks for Time-Frequency Channel Diagonalization. EURASIP J. Adv. Signal Process. 2010, 172751 (2010). https://doi.org/10.1155/2010/172751
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/172751

 representable by matrices
representable by matrices  with maximal polynomial order P − 1 for J = 3, L = 4, P = 1, 2.
with maximal polynomial order P − 1 for J = 3, L = 4, P = 1, 2.
 ,
,  .
. complying with the WSSUS model and unit average channel gain (i.e.,
complying with the WSSUS model and unit average channel gain (i.e., 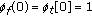 ).
).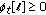 for all
for all  , as being the case for two-sided exponentially decaying and many other symmetrical Doppler power spectra.
, as being the case for two-sided exponentially decaying and many other symmetrical Doppler power spectra.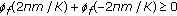 for all
for all  , as, for instance, in the case of exponentially decaying delay power spectra.
, as, for instance, in the case of exponentially decaying delay power spectra.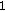 , we resort to the matrix
, we resort to the matrix  composed by the dominant eigenvector
composed by the dominant eigenvector  of
of 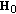 , since
, since 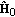 is the matrix nearest to
is the matrix nearest to  in terms of the Frobenius norm [
in terms of the Frobenius norm [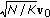 into a window
into a window 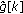 taking the sample permutation defined in (29) into account.
taking the sample permutation defined in (29) into account. by the algorithm [
by the algorithm [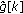 ) in terms of the
) in terms of the  -norm.
-norm.
 ,
,  (in (a) and (c)),
(in (a) and (c)),  ,
,  (in (b) and (d)).
(in (b) and (d)).
 and
and  optimized through CO and SDP, respectively, and by window
optimized through CO and SDP, respectively, and by window  with RRC-shaped magnitude spectrum versus
with RRC-shaped magnitude spectrum versus  at
at  .
.
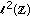 . IEEE Transactions on Signal Processing 1998, 46(5):1256-1259. 10.1109/78.668789
. IEEE Transactions on Signal Processing 1998, 46(5):1256-1259. 10.1109/78.668789