- Research Article
- Open access
- Published:
Constellation Design for Widely Linear Transceivers
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 176587 (2010)
Abstract
Constellation design has been previously addressed by assuming that there is a linear equalizer at the receiver side. However, the widely linear equalizer is well known to outperform the linear one with no significant complexity increase; we derive optimum and suboptimum techniques for constellation design in presence of such an equalizer. The proposed techniques adapt the circularity properties of the transmitted signals to the specific channel to be equalized; their performance analysis shows that also the simplest suboptimum procedure provides significant improvements over a fixed-constellation scheme.
1. Introduction
Constellation design has been previously addressed by assuming that there is a linear equalizer at the receiver side. In early works (see, e.g., [1, 2]), the optimization of a two-dimensional constellation in order to minimize the symbol error rate (SER) was first addressed with reference to the transmission over a nondispersive channel affected by additive noise.
The advantage provided by the constellations with two degrees of freedom (such as quadrature amplitude modulation (QAM)) over the ones with one degree of freedom (such as phase-shift-keying (PSK), and pulse amplitude modulation (PAM)) was shown [1], and a proper mapping (based on a gradient-descent procedure) of the  information bits into
information bits into  points of a two-dimensional constellation was proposed [2]. However, the adoption of an additive-noise nondispersive channel model allows one to consider the constellation mapping independently of the equivalent channel. On the other hand, an amount of literature (e.g., [3–7]) refers to the optimization of the transmitter and/or the receiver without including the choice of the constellation in the optimization procedure. In fact, many existing transceiver processing techniques are optimized (according to a chosen criterion) by only exploiting knowledge of the statistics of the information symbol sequence.
points of a two-dimensional constellation was proposed [2]. However, the adoption of an additive-noise nondispersive channel model allows one to consider the constellation mapping independently of the equivalent channel. On the other hand, an amount of literature (e.g., [3–7]) refers to the optimization of the transmitter and/or the receiver without including the choice of the constellation in the optimization procedure. In fact, many existing transceiver processing techniques are optimized (according to a chosen criterion) by only exploiting knowledge of the statistics of the information symbol sequence.
This paper addresses the constellation design under the assumption that the transmitter is fixed (i.e., by considering an equivalent channel representing the transmitter and the channel) and a widely linear (WL) minimum mean square error (MMSE) equalizer is employed at the receiver side [8–14].
The WL filtering generalizes the conventional linear filtering and allows one to achieve a power reduction of the additive noise and interferences at the equalizer output, and therefore a performance gain, by exploiting the statistical redundancy possibly exhibited by a rotationally variant transmitted (and/or received) signal. For such a reason, the adoption of the WL equalization has frequently been confined to the transmission of one-dimensional constellations (see, e.g., [3, 15–17] and references therein) since the advantage of using the WL filtering (instead of the linear one) is maximum for one-dimensional constellation. Two-dimensional constellations (especially high-order ones) are often preferred to one-dimensional constellations (in presence of a linear receiver) in order to maximize the minimum distance between the constellation points [1]. However, WL linear filtering provides no performance advantage over linear one when the chosen constellation and the additive noise are circularly symmetric. For such a reason, we consider the optimization both over circularly symmetric and over rotationally variant constellations without any assumption about the circularity properties of the additive noise. In fact, the noncircularity of the constellation is introduced in order to exploit the presence of the WL receiver but it also provides a disadvantage in terms of the minimum distance between the constellation points.
When both the effects are accounted for, the optimum degree of noncircularity of the constellation becomes dependent on the specific channel impulse response. Therefore, we address the constellation design under the assumption that the channel state information (CSI) is available and we propose a CSI-dependent symbol mapping that optimizes the performance of the WL MMSE receiver. Symbol mapping is adapted by using a feedback channel (between the receiver and the transmitter) carrying information about the optimum constellation. Moreover, suboptimum strategies are proposed in order to reduce both the amount of information to be transmitted on the feedback channel and the computational complexity of the optimization procedure.
The paper is organized as follows. Section 2 introduces the system model, recalls the MMSE equalizer structure and analyzes how its performance depends on the amount of pseudocorrelation of the transmitted signal. Section 3 addresses the constellation design in the presence of the WL MMSE equalizer by generalizing the results in [2] to the case where the additive disturbance (noise plus interference) is rotationally variant. Section 4 reports the results of simulation experiments mainly aimed at showing the performance advantages provided by the constellation adaptation procedures. Finally, Section 5 provides the conclusions and the final remarks.
Notation 1.
The following notations are adopted throughout the paper.  is the imaginary unit, the superscripts
is the imaginary unit, the superscripts  ,
,  , and
, and  denote the complex-conjugate, the transpose and the Hermitian transpose, respectively,
denote the complex-conjugate, the transpose and the Hermitian transpose, respectively,  is the statistical expectation,
is the statistical expectation,  is the Kronecker delta,
is the Kronecker delta,  is the identity matrix of size
is the identity matrix of size  ,
,  is the vector/matrix with all zero entries (the size is omitted for brevity),
is the vector/matrix with all zero entries (the size is omitted for brevity),  denotes the
denotes the  th entry of the vector
th entry of the vector  ,
,  denotes the
denotes the  entry of the matrix
entry of the matrix  ,
,  denotes the
denotes the  th column of
th column of  ,
,  and
and  are the real and the imaginary part, respectively,
are the real and the imaginary part, respectively,  denotes the
denotes the  -norm with
-norm with  , and, finally,
, and, finally,  is the
is the  -transform of
-transform of  .
.
2. The FIR MMSE Equalizer
In this section, we introduce the considered system model; then, we derive the WL MMSE feedforward-based equalizer and we study the variations of the achieved MMSE versus the pseudocorrelation of the transmitted signal. Such an analysis will be useful in Section 3 to address the constellation design for MMSE receivers.
2.1. System Model
Let us consider the following finite-impulse-response (FIR) baseband-equivalent noisy communication channel

where the transmitted symbols  are independent identically distributed (i.i.d.) zero-mean random variables drawn from the complex-valued constellation
are independent identically distributed (i.i.d.) zero-mean random variables drawn from the complex-valued constellation  whose (finite) order
whose (finite) order  determines the bit rate (
determines the bit rate ( bits per symbol) of the uncoded system part. With no loss of generality, we assume that
bits per symbol) of the uncoded system part. With no loss of generality, we assume that  and
and  , that is, the transmitted available power is unit, and that
, that is, the transmitted available power is unit, and that  exhibits a possibly nonnull pseudocorrelation
exhibits a possibly nonnull pseudocorrelation  , such that
, such that  (if
(if  , then the correlation matrix of the
, then the correlation matrix of the  random vector
random vector  will be positive semidefinite); note that the noncircularity of
will be positive semidefinite); note that the noncircularity of  consists in the difference between the power of the in-phase component and the quadrature one and in the correlation between them. Such assumption allows one to consider both the conventional circularly symmetric constellations (
consists in the difference between the power of the in-phase component and the quadrature one and in the correlation between them. Such assumption allows one to consider both the conventional circularly symmetric constellations ( ), such as
), such as  -PSK and square
-PSK and square  -QAM with
-QAM with  , and the rotationally variant constellations, such as the well-known PAM (
, and the rotationally variant constellations, such as the well-known PAM ( ) and its rotated version (for which it exists
) and its rotated version (for which it exists  such that
such that  is real-valued and, consequently,
is real-valued and, consequently,  ), non-square QAM (with
), non-square QAM (with  since a different power is allocated to the in-phase and quadrature components). The time-invariant FIR channel impulse response
since a different power is allocated to the in-phase and quadrature components). The time-invariant FIR channel impulse response  of memory
of memory  is assumed to be known at the receiver side. Finally, the additive noise
is assumed to be known at the receiver side. Finally, the additive noise  , whose power
, whose power  is assumed known at the receiver, is modeled as zero-mean complex-valued wide-sense stationary time-uncorrelated and independent of the useful signal. The additive disturbance
is assumed known at the receiver, is modeled as zero-mean complex-valued wide-sense stationary time-uncorrelated and independent of the useful signal. The additive disturbance  is not assumed circularly symmetric because it may include the effects of one-dimensional cochannel interferences.
is not assumed circularly symmetric because it may include the effects of one-dimensional cochannel interferences.
At the receiver side, the feedforward-based equalization is performed by processing the block of  received samples
received samples  which, in a matrix notation, can be written as follows:
which, in a matrix notation, can be written as follows:

According to the previous assumptions, the following correlation and pseudocorrelation matrices can be written as

where  is the (possibly) nonnull noise pseudocorrelation (if
is the (possibly) nonnull noise pseudocorrelation (if  , then the noise is circularly symmetric).
, then the noise is circularly symmetric).
2.2. Feedforward-Based MMSE Equalizer
Since the transmitted sequence  and consequently the received one
and consequently the received one  in (1) can be rotationally variant, we adopt a widely linear receiver in order to exploit the statistical redundancy exhibited by the received signal. Note that such a choice improves the performance since the linear equalizers are a subset of the WL equalizers; their performances coincide only in the presence of circularly symmetric signals [10]. Therefore, we resort to the two FIR filters
in (1) can be rotationally variant, we adopt a widely linear receiver in order to exploit the statistical redundancy exhibited by the received signal. Note that such a choice improves the performance since the linear equalizers are a subset of the WL equalizers; their performances coincide only in the presence of circularly symmetric signals [10]. Therefore, we resort to the two FIR filters  and
and  that process the received vector
that process the received vector  and its complex conjugate version
and its complex conjugate version  , respectively. The optimum filters
, respectively. The optimum filters  and
and  minimizing the mean square error
minimizing the mean square error  are given by [16, 18]
are given by [16, 18]


where  denotes the
denotes the  th column of
th column of  and the processing delay
and the processing delay  has to be chosen in order to optimize the performance. For notational simplicity, in (4) and (5) we have omitted the dependence of
has to be chosen in order to optimize the performance. For notational simplicity, in (4) and (5) we have omitted the dependence of  and
and  on
on  . Let us point out that when
. Let us point out that when  , that is, the transmitted symbols are drawn from a circularly symmetric constellation,
, that is, the transmitted symbols are drawn from a circularly symmetric constellation,  = 0 and, therefore, the WL MMSE equalizer degenerates into the conventional linear MMSE equalizer. Another special case is represented by the scenario where a real-valued constellation is adopted. In fact, since
= 0 and, therefore, the WL MMSE equalizer degenerates into the conventional linear MMSE equalizer. Another special case is represented by the scenario where a real-valued constellation is adopted. In fact, since  ,
,  and the WL MMSE equalizer becomes
and the WL MMSE equalizer becomes  , that is, it is implemented by extracting the in-phase component of the linear equalizer
, that is, it is implemented by extracting the in-phase component of the linear equalizer  , which does not coincide, however, with the linear MMSE equalizer.
, which does not coincide, however, with the linear MMSE equalizer.
Since the optimum equalizer and, hence, its performance depends on the pseudocorrelation  of the transmitted signal, let us analyze the dependence on
of the transmitted signal, let us analyze the dependence on  of the MMSE. To this end, denote with
of the MMSE. To this end, denote with  the error measured at the output of the WL MMSE equalizer for given values of
the error measured at the output of the WL MMSE equalizer for given values of  and
and  . It can be easily shown that
. It can be easily shown that


Since  is the MMSE at the outputs of both the WL MMSE equalizer and the linear MMSE equalizer in the presence of a circularly symmetric constellation,
is the MMSE at the outputs of both the WL MMSE equalizer and the linear MMSE equalizer in the presence of a circularly symmetric constellation,  represents the MMSE gain achieved by properly choosing the pseudocorrelation
represents the MMSE gain achieved by properly choosing the pseudocorrelation  of the transmitted constellation. When
of the transmitted constellation. When  , that is, the noise is circularly symmetric,
, that is, the noise is circularly symmetric,  depends on
depends on  instead of
instead of  and its (first) derivative with respect to
and its (first) derivative with respect to  can be written as
can be written as

Since  and
and  are positive semidefinite, one has
are positive semidefinite, one has  and, hence, increasing the degree of noncircularity of the transmitted signal improves the MMSE. For such a reason, the use of a real-valued transmitted sequence together with a WL MMSE equalizer corresponds to the optimum choice as far as the MMSE is adopted as the performance measure. On the other hand, when
and, hence, increasing the degree of noncircularity of the transmitted signal improves the MMSE. For such a reason, the use of a real-valued transmitted sequence together with a WL MMSE equalizer corresponds to the optimum choice as far as the MMSE is adopted as the performance measure. On the other hand, when  , the variations of
, the variations of  with respect to
with respect to  depend on the specific values of the channel impulse response and the noise statistics.
depend on the specific values of the channel impulse response and the noise statistics.
3. Constellation Design
The present section addresses the design of the  -order constellation with
-order constellation with  fixed (under the assumption that the WL MMSE equalizer is used) and it is organized as follows. In Section 3.1, we address the optimum constellation design for the WL MMSE receiver by extending the results of [2] to the case of additive rotationally variant disturbance. In Section 3.2, we propose a suboptimum strategy based on the rhombic transformation of a given constellation. Such a strategy allows one to reduce both the computational complexity of the optimization procedure and the amount of information required at the transmitting side in order to adapt the constellation.
fixed (under the assumption that the WL MMSE equalizer is used) and it is organized as follows. In Section 3.1, we address the optimum constellation design for the WL MMSE receiver by extending the results of [2] to the case of additive rotationally variant disturbance. In Section 3.2, we propose a suboptimum strategy based on the rhombic transformation of a given constellation. Such a strategy allows one to reduce both the computational complexity of the optimization procedure and the amount of information required at the transmitting side in order to adapt the constellation.
The results in the previous section allow one to state that, by using a real-valued constellation ( ) instead of a complex-valued nonredundant (
) instead of a complex-valued nonredundant ( ) one, a performance gain can be achieved in terms of the MMSE at the equalizer output. On the other hand, not always an MSE gain provided by the WL equalizer leads to a SER gain [19]. In fact, for a fixed expended average energy per bit, the reduction of the minimum distance between the constellation points, due to the adoption of one-dimensional constellations rather than two-dimensional ones (e.g., when we adopt the
) one, a performance gain can be achieved in terms of the MMSE at the equalizer output. On the other hand, not always an MSE gain provided by the WL equalizer leads to a SER gain [19]. In fact, for a fixed expended average energy per bit, the reduction of the minimum distance between the constellation points, due to the adoption of one-dimensional constellations rather than two-dimensional ones (e.g., when we adopt the  -PAM rather than the
-PAM rather than the  -QAM) leads to a potential increase in the SER. Therefore, we address the constellation design minimizing the SER at the WL MMSE equalizer output by accounting for its rotationally variant properties.
-QAM) leads to a potential increase in the SER. Therefore, we address the constellation design minimizing the SER at the WL MMSE equalizer output by accounting for its rotationally variant properties.
In the literature (e.g., [2, 20]), most of the constellations employed by the transmission stage are circularly symmetric ( ), while statistically redundant constellations are confined to the real-valued ones. Moreover, in [2], with reference to the transmission over a time nondispersive channel (
), while statistically redundant constellations are confined to the real-valued ones. Moreover, in [2], with reference to the transmission over a time nondispersive channel ( ) affected by circularly symmetric noise, a procedure for constellation optimization has been proposed, showing also that, for large signal-to-noise ratios (SNR), the performance of the conventional QAM maximum-likelihood (ML) receiver is invariant with respect to rhombic transformations of the complex plane. However, it is important to point out that a rhombic transformation of a circular constellation makes it rotationally variant and, for some values of
) affected by circularly symmetric noise, a procedure for constellation optimization has been proposed, showing also that, for large signal-to-noise ratios (SNR), the performance of the conventional QAM maximum-likelihood (ML) receiver is invariant with respect to rhombic transformations of the complex plane. However, it is important to point out that a rhombic transformation of a circular constellation makes it rotationally variant and, for some values of  (e.g.,
(e.g.,  ), the procedure in [2] provides a rotationally variant constellation. On the other hand, the WL equalizer is equivalent to the linear equalizer over the nondispersive channel considered in [2] and, therefore, optimizing the circularity degree of the constellation does not provide any performance advantage. On the other hand, when a time-dispersive channel is considered, the WL MMSE equalizer is sensitive to the rotationally variant properties of the transmitted signal and, therefore, we propose a transceiver structure (see Figure 1) where (i) the transmitter can switch between the available constellations of order
), the procedure in [2] provides a rotationally variant constellation. On the other hand, the WL equalizer is equivalent to the linear equalizer over the nondispersive channel considered in [2] and, therefore, optimizing the circularity degree of the constellation does not provide any performance advantage. On the other hand, when a time-dispersive channel is considered, the WL MMSE equalizer is sensitive to the rotationally variant properties of the transmitted signal and, therefore, we propose a transceiver structure (see Figure 1) where (i) the transmitter can switch between the available constellations of order  ; (ii) the WL MMSE receiver accounts for the CSI and informs the transmitter, by means of a feedback channel, about which constellation has to be adopted to minimize the SER.
; (ii) the WL MMSE receiver accounts for the CSI and informs the transmitter, by means of a feedback channel, about which constellation has to be adopted to minimize the SER.
The use of a feedback channel in order to improve the bit-rate could also be exploited for choosing the constellation size rather than its circularity degree when the signal-to-noise ratio of each channel realization is not previously known. For example, the problem of the constellation choice has been addressed in [21, 22] with reference to the discrete multitone (DMT) transceiver and to multiple-input multiple-output transceiver, respectively. The two parameters of the constellations (size and circularity-degree) could also be jointly optimized by generalizing the procedures here proposed.
3.1. Constellation Optimization in the Presence of Gaussian Rotationally Variant Noise
In order to optimize over the constellation choice we need to first derive a performance analysis of the considered equalizer. Approximated evaluations of the performance of the WL receiver are available in [11] for a QAM constellation and in [3] for a PAM constellation in the presence of a PAM cochannel interference. Moreover, such performance analysis is generalized in [9] for IIR WL filters. Here, we derive an approximation of the equalizer performance suited for successive optimization over transmitter constellation.
With no loss of generality, assume that  and rewrite the output of the FIR equalizer as follows:
and rewrite the output of the FIR equalizer as follows:

where  is the transmitted symbol drawn from the complex-valued constellation
is the transmitted symbol drawn from the complex-valued constellation  with
with  and
and  , and
, and  is the residual disturbance that includes the intersymbol interference and the noise terms after the WL equalizer filtering. The circularly symmetric model for the additive disturbance is inadequate since the output of a WL filter is, in general, rotationally variant. Therefore, we model
is the residual disturbance that includes the intersymbol interference and the noise terms after the WL equalizer filtering. The circularly symmetric model for the additive disturbance is inadequate since the output of a WL filter is, in general, rotationally variant. Therefore, we model  as rotationally variant, that is,
as rotationally variant, that is,  ,
,  , and
, and  . Moreover, in order to make the constellation design analytically tractable, we approximate
. Moreover, in order to make the constellation design analytically tractable, we approximate  as Gaussian. For the sake of clarity, let us note that, if symbols
as Gaussian. For the sake of clarity, let us note that, if symbols  and noise are circularly symmetric (
and noise are circularly symmetric ( ), then the additive disturbance
), then the additive disturbance  and the equalizer output
and the equalizer output  will be circularly symmetric too; on the other hand, if
will be circularly symmetric too; on the other hand, if  is rotationally variant, then
is rotationally variant, then  will be rotationally variant too, but nothing can be stated about the circularity properties of
will be rotationally variant too, but nothing can be stated about the circularity properties of  also when
also when  .
.
The sample  is the input of the decision device which performs the symbol-by-symbol ML detection of the transmitted symbol. By defining the following eigenvalue decomposition (the dependence on
is the input of the decision device which performs the symbol-by-symbol ML detection of the transmitted symbol. By defining the following eigenvalue decomposition (the dependence on  at the right-hand-side is omitted for simplicity):
at the right-hand-side is omitted for simplicity):

with  being the eigenvector matrix and
being the eigenvector matrix and  having on the diagonal the eigenvalues, it can be verified that the pair-wise error probability
having on the diagonal the eigenvalues, it can be verified that the pair-wise error probability  [20], that is, the probability of transmitting
[20], that is, the probability of transmitting  and deciding (at the receiver) in favor of
and deciding (at the receiver) in favor of  when the transmission system uses only
when the transmission system uses only  and
and  , is given by
, is given by

where  denotes
denotes  +
+  where
where  and
and  , and, for
, and, for  and
and  ,
,

When  ,
,  and analogously for
and analogously for  and
and  . By utilizing (11), assuming that the symbols
. By utilizing (11), assuming that the symbols  are equally probable, and resorting to both the union bound and Chernoff bound techniques, the SER
are equally probable, and resorting to both the union bound and Chernoff bound techniques, the SER  is upper-bounded as follows:
is upper-bounded as follows:

and, therefore, the optimum constellation can be approximated with the solution  of the following problem:
of the following problem:

Unfortunately, it is difficult to find the closed-form expression of the solution of such an optimization problem. For such a reason, we propose to find a local solution by means of numerical algorithms (e.g., a projected gradient method). To this aim, we can exploit the gradient of  with respect to
with respect to  , while we resort to numerical approximation of the gradient with respect to
, while we resort to numerical approximation of the gradient with respect to  since it is difficult to obtain its analytical expression.
since it is difficult to obtain its analytical expression.
Before proceeding, let us discuss the property of the locally optimum constellation for a fixed  . The
. The  th component of the gradient of
th component of the gradient of  is given by
is given by

By zeroing the gradient of the Lagrangian

one has that the locally optimum  satisfies the following equation:
satisfies the following equation:

with

Condition (17) generalizes the result of [2] to the case of  rotationally variant (i.e.,
rotationally variant (i.e.,  or
or  ) and with a constrained pseudocorrelation. (
) and with a constrained pseudocorrelation. ( .) In fact, (17) with
.) In fact, (17) with  (i.e., no constraint is imposed on the pseudocorrelation) requires that
(i.e., no constraint is imposed on the pseudocorrelation) requires that  is proportional to the weighted sum (with weights
is proportional to the weighted sum (with weights  ) of
) of  ,
,  , as found in [2]. For the sake of clarity, let us note that the procedure proposed in [2] does not allow one to exploit the potential advantage of a rotationally variant constellation when the WL MMSE receiver is employed. For example, when a linear MMSE equalizer is employed for
, as found in [2]. For the sake of clarity, let us note that the procedure proposed in [2] does not allow one to exploit the potential advantage of a rotationally variant constellation when the WL MMSE receiver is employed. For example, when a linear MMSE equalizer is employed for  in high signal-to-noise ratio, the minimum of the SER is equivalently achieved [2] by both the conventional 4-QAM constellation and the rhombic constellations with the same perimeter, that is, the perimeter of the largest convex polygon consisting of the lines
in high signal-to-noise ratio, the minimum of the SER is equivalently achieved [2] by both the conventional 4-QAM constellation and the rhombic constellations with the same perimeter, that is, the perimeter of the largest convex polygon consisting of the lines  (see [1] for further details). On the other hand, when a WL MMSE equalizer is employed, a rhombic constellation, which is rotationally variant, is not equivalent to the conventional 4-QAM since the achieved MMSE is dependent on
(see [1] for further details). On the other hand, when a WL MMSE equalizer is employed, a rhombic constellation, which is rotationally variant, is not equivalent to the conventional 4-QAM since the achieved MMSE is dependent on  as shown in (8).
as shown in (8).
3.2. A Suboptimum Procedure Based on Rhombic Transformations
In this section, we propose a suboptimum constellation-design procedure for the WL MMSE equalizer. The method is based on the exploitation of a rhombic transformation that operates on a circularly symmetric constellation making it rotationally variant. Such a transformation depends on two parameters and allows one to control the pseudocorrelation  of the obtained constellation; consequently, the optimization procedure is simplified since the SER in (13) is a function of only two parameters, instead of
of the obtained constellation; consequently, the optimization procedure is simplified since the SER in (13) is a function of only two parameters, instead of  parameters.
parameters.
Assume that  is a unit-power circularly-symmetric complex-valued constellation and define the complex-valued constellation
is a unit-power circularly-symmetric complex-valued constellation and define the complex-valued constellation  as follows:
as follows:

or, more compactly (the compact expression is introduced for notation simplicity whereas the matrix form is utilized to understand the physical meaning),

with  and
and  . When
. When  (
( ),
),  is stretched along the in-phase (quadrature) component and it becomes one-dimensional for
is stretched along the in-phase (quadrature) component and it becomes one-dimensional for  ; when
; when  , a correlation between
, a correlation between  and
and  is introduced and for
is introduced and for  , even if it is two-dimensional,
, even if it is two-dimensional,  can be reduced to a one-dimensional constellation by a simple rotation. For symmetry, in the following we consider only the positive values of
can be reduced to a one-dimensional constellation by a simple rotation. For symmetry, in the following we consider only the positive values of  and
and  . It is easily verified that, if
. It is easily verified that, if  is drawn from
is drawn from  , then
, then

The method proposed here assumes that the information-bearing symbol sequence, say  , is drawn from a fixed constellation
, is drawn from a fixed constellation  (e.g., the optimum constellation provided by [2]) whereas the possibly rotationally variant channel input
(e.g., the optimum constellation provided by [2]) whereas the possibly rotationally variant channel input  is obtained by resorting to the zero-memory precoding defined by the rhombic transformation (19). Clearly, such a strategy is suboptimum since it assumes that the channel input can be drawn from only those constellations
is obtained by resorting to the zero-memory precoding defined by the rhombic transformation (19). Clearly, such a strategy is suboptimum since it assumes that the channel input can be drawn from only those constellations  resulting from a rhombic transformation of the chosen
resulting from a rhombic transformation of the chosen  . However, the main advantages of such a method in comparison with the optimum one are
. However, the main advantages of such a method in comparison with the optimum one are
-
(1)
the huge reduction of the computational complexity of the constellation optimization procedure when
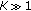 ; in fact, the SER becomes a function of only two variables (
; in fact, the SER becomes a function of only two variables ( and
and  ), regardless of the constellation order
), regardless of the constellation order 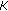 ;
; -
(2)
the reduced implementation complexity of the transmitter stage; in fact, the symbol-mapping is implemented by means of the linear transformation (19);
-
(3)
the decrease of the information amount to be transmitted on the feedback channel; in fact, only the values of two parameters (instead of
 ) have to be sent to the transmitter.
) have to be sent to the transmitter.
According to such a choice, the constellation optimization is carried out by solving the minimization problem

with

where  denotes
denotes  ,
,  denotes
denotes  −
−  , and
, and  denotes
denotes  +
+  −
−  −
−  −
−  , and where (23) follows from (13) and (19), and the dependence of the disturbance parameters on
, and where (23) follows from (13) and (19), and the dependence of the disturbance parameters on  has been replaced by the dependence on
has been replaced by the dependence on  and
and  . Since finding the closed-form expression of
. Since finding the closed-form expression of  and
and  is a difficult problem, here we propose to approximate
is a difficult problem, here we propose to approximate  with a function, say
with a function, say  , whose minimization can be carried out by evaluating it only over a very limited set of points. In the sequel, such an approximation is derived for a
, whose minimization can be carried out by evaluating it only over a very limited set of points. In the sequel, such an approximation is derived for a  -QAM constellation
-QAM constellation  , though it can be analogously determined for denser constellations.
, though it can be analogously determined for denser constellations.
First, we approximate the cost function (23) by assuming that the components of the residual disturbance are uncorrelated, that is,  . By means of some tedious but simple algebra operations, it can be shown that
. By means of some tedious but simple algebra operations, it can be shown that  is lower bounded by
is lower bounded by

where

where  denotes
denotes  and
and  denotes
denotes  . Since the right-hand side of (24) is minimized by large values of
. Since the right-hand side of (24) is minimized by large values of  , we propose to approximate the solution of (22) with the following one:
, we propose to approximate the solution of (22) with the following one:

where  is the
is the  -curve corresponding to the maximum value of
-curve corresponding to the maximum value of  for a fixed
for a fixed  (or, equivalently, to the maximum value of
(or, equivalently, to the maximum value of  for a fixed
for a fixed  ). Of course, the restriction to
). Of course, the restriction to  leads to a significant decrease in the computational complexity. Let us point out that, interestingly, such a restricted optimization procedure accounts for the possible transmission of the conventional 4-PAM: in fact, it can be easily verified that when
leads to a significant decrease in the computational complexity. Let us point out that, interestingly, such a restricted optimization procedure accounts for the possible transmission of the conventional 4-PAM: in fact, it can be easily verified that when  ,
,  .
.
This also suggests an extreme simplification obtained by choosing just between the 4-PAM and 4-QAM constellation (two-choice procedure), that is, one can resort to an architecture that switches between the 4-QAM and the 4-PAM constellations according to the following rule:

Three remarks about the suboptimum procedure (26) follow.
Remark 1.
The results carried out here with reference to the  -QAM constellation can be easily generalized to higher-order constellations. More specifically, the SER-bound approximations (analogous to the one in (24)) can be obtained by assuming that the inner summation in (23) is restricted to those constellation points closest to the
-QAM constellation can be easily generalized to higher-order constellations. More specifically, the SER-bound approximations (analogous to the one in (24)) can be obtained by assuming that the inner summation in (23) is restricted to those constellation points closest to the  th one. Moreover, it can be shown that the conventional square
th one. Moreover, it can be shown that the conventional square  -QAM constellations (with
-QAM constellations (with  ) can be transformed by (19) into the conventional uniform
) can be transformed by (19) into the conventional uniform  -PAM. Note, however, that such a property is not satisfied by the constellations of any order; for example, as also shown in Section 4, when using the rectangular
-PAM. Note, however, that such a property is not satisfied by the constellations of any order; for example, as also shown in Section 4, when using the rectangular  -QAM (see Figure 2(g)) the rhombic transformation allows one to obtain the nonuniform
-QAM (see Figure 2(g)) the rhombic transformation allows one to obtain the nonuniform  -PAM reported in Figure 2(i).
-PAM reported in Figure 2(i).
Remark 2.
The optimum transmission strategy proposed here requires that the receiver sends on the feedback channel the whole optimum constellation. If the suboptimum procedure is used, the transmitter architecture can be simplified. In fact, a unique symbol mapper for the alphabet  is needed and the constellation is adapted by adjusting the zero-memory WL filter (19). Unfortunately, the main disadvantage in terms of the computational complexity of the receiver remains the adaptation of the decision mechanism for the constellation
is needed and the constellation is adapted by adjusting the zero-memory WL filter (19). Unfortunately, the main disadvantage in terms of the computational complexity of the receiver remains the adaptation of the decision mechanism for the constellation  .
.
Remark 3.
When the proposed suboptimum strategy is used, the channel input  is obtained by performing a zero-memory WL filtering of the information-bearing sequence
is obtained by performing a zero-memory WL filtering of the information-bearing sequence  . For such a reason, it is reasonable to consider an alternative receiver structure that performs the WL MMSE equalization of the received signal in order to estimate
. For such a reason, it is reasonable to consider an alternative receiver structure that performs the WL MMSE equalization of the received signal in order to estimate  , instead of
, instead of  . After some matrix manipulations, it can be verified that such WL MMSE equalizer is the cascade of the WL MMSE equalizer in (4) and (5) and the WL zero-memory filter performing the inverse of the transformation (19) (note that (19) is not invertible for every value of
. After some matrix manipulations, it can be verified that such WL MMSE equalizer is the cascade of the WL MMSE equalizer in (4) and (5) and the WL zero-memory filter performing the inverse of the transformation (19) (note that (19) is not invertible for every value of  and
and  , e.g., when a real-valued constellation is adopted (
, e.g., when a real-valued constellation is adopted ( ), however, in such a case, an ad hoc inverse transformation can be easily defined). This allows one to use a unique symbol de-mapper and the standard decision mechanism for the constellation
), however, in such a case, an ad hoc inverse transformation can be easily defined). This allows one to use a unique symbol de-mapper and the standard decision mechanism for the constellation  . The MMSE achieved by such a structure is
. The MMSE achieved by such a structure is

It can be easily shown that (a) if  , then
, then  , unless
, unless  , and (b)
, and (b)  since
since  . Such results show that the minimum-distance decision based on the WL MMSE estimation of
. Such results show that the minimum-distance decision based on the WL MMSE estimation of  outperforms the (computationally simpler) minimum-distance decision based on the WL MMSE estimation of
outperforms the (computationally simpler) minimum-distance decision based on the WL MMSE estimation of  .
.
4. Numerical Results
In this section, we present the results of simulation experiments aimed at assessing the performance improvements achievable by the proposed constellation-optimization procedures. In all the experiments, we assume that ( ) the noise sequence at the output of the channel is zero-mean white Gaussian complex-valued circularly symmetric with variance
) the noise sequence at the output of the channel is zero-mean white Gaussian complex-valued circularly symmetric with variance  , that is,
, that is, 
 ; (
; ( ) the decision delay
) the decision delay  is optimized; (
is optimized; ( ) the SER has been estimated by stopping the simulation after 100 errors occur; (
) the SER has been estimated by stopping the simulation after 100 errors occur; ( ) each sample at the output of the WL filter is the input of the decision device that performs the symbol-by-symbol ML detection of the transmitted symbol.
) each sample at the output of the WL filter is the input of the decision device that performs the symbol-by-symbol ML detection of the transmitted symbol.
4.1. Fixed Channel
In this section, we compare the performances of the constellation design procedures (26) and (14) in terms of SER. In our simulations, we solve (26) by means of an exhaustive search over  and
and  : note that in our search we consider
: note that in our search we consider  , so we consider a finite number of points. On the other hand, we resort to the constrained gradient-based algorithm for solving (14). Since the cost function (13) exhibits local minima, 1000 starting points have been randomly generated according to a uniform distribution. Due to the amount of time required by the computer simulations to determine the solution of (14), we consider, as in [16], the transmission over a two-tap channel
, so we consider a finite number of points. On the other hand, we resort to the constrained gradient-based algorithm for solving (14). Since the cost function (13) exhibits local minima, 1000 starting points have been randomly generated according to a uniform distribution. Due to the amount of time required by the computer simulations to determine the solution of (14), we consider, as in [16], the transmission over a two-tap channel  affected by an additive circularly symmetric white Gaussian noise with variance
affected by an additive circularly symmetric white Gaussian noise with variance  . In our experiments, we have addressed the optimization of the constellation when
. In our experiments, we have addressed the optimization of the constellation when  and
and  for different values of
for different values of  ,
,  , and
, and  .
.
Let us first plot in Figure 2 some of the optimum constellations obtained during our simulations when solving the optimization problem (14) over the considered channel model; moreover, we plot the suboptimum constellation utilized to implement our suboptimum strategy and the  -PAM constellation obtained by applying to it the rhombic transformation. As in [2], we have found many local optima, some of them were rotated version of the constellations of Figure 2 while others appeared as their rhombic transformation. For
-PAM constellation obtained by applying to it the rhombic transformation. As in [2], we have found many local optima, some of them were rotated version of the constellations of Figure 2 while others appeared as their rhombic transformation. For  the locally optimum constellation set includes the conventional
the locally optimum constellation set includes the conventional  -QAM (
-QAM ( ) and
) and  -PAM (
-PAM ( ), as well as the
), as well as the  -QAM subject to a rhombic transformation (
-QAM subject to a rhombic transformation ( ); note that such constellations can be obtained by means of a rhombic transformation of the conventional
); note that such constellations can be obtained by means of a rhombic transformation of the conventional  -QAM (as also shown in Section 3.2), which has been utilized to implement our suboptimum strategy when
-QAM (as also shown in Section 3.2), which has been utilized to implement our suboptimum strategy when  . For
. For  , the optimum constellation set includes the noncircular
, the optimum constellation set includes the noncircular  -QAM found by Foschini et al. (
-QAM found by Foschini et al. ( ), one of the conventional
), one of the conventional  -QAM scheme (
-QAM scheme ( ) called "1-7" 8-QAM [2], the
) called "1-7" 8-QAM [2], the  -PAM (
-PAM ( ) and the noncircular
) and the noncircular  -QAM scheme that we call noncircular 8-QAM. In the following, in order to implement the rhombic-transformation-based constellation-optimization strategy, we resort to the rectangular
-QAM scheme that we call noncircular 8-QAM. In the following, in order to implement the rhombic-transformation-based constellation-optimization strategy, we resort to the rectangular  -QAM; we remember that, unlike
-QAM; we remember that, unlike  -QAM, such a scheme cannot be transformed into the conventional uniform
-QAM, such a scheme cannot be transformed into the conventional uniform  -PAM, but in the nonoptimum nonuniform
-PAM, but in the nonoptimum nonuniform  -PAM (the optimality of uniform PAM over additive white Gaussian noise has been shown in [23]).
-PAM (the optimality of uniform PAM over additive white Gaussian noise has been shown in [23]).
In Figure 3, with reference to the case  , we have set
, we have set  and we have plotted the SERs achieved by both the suboptimum strategy (26) and the optimum strategy (14) versus
and we have plotted the SERs achieved by both the suboptimum strategy (26) and the optimum strategy (14) versus  , for
, for  and for different values of
and for different values of  (
( ); moreover, for each point of Figure 3, the constellation typically obtained by the optimum procedure is specified by the letter used to denote it in Figure 2. The results show that the two strategies have the same performance: more specifically, both strategies switch to the
); moreover, for each point of Figure 3, the constellation typically obtained by the optimum procedure is specified by the letter used to denote it in Figure 2. The results show that the two strategies have the same performance: more specifically, both strategies switch to the  -PAM when
-PAM when  and outperform the conventional nonadaptive transceiver employing the QPSK modulation jointly with the linear MMSE receiver. Note also that as
and outperform the conventional nonadaptive transceiver employing the QPSK modulation jointly with the linear MMSE receiver. Note also that as  , the chosen value of
, the chosen value of  does not affect the performance.
does not affect the performance.
Constellation optimization for K=4 over fixed channel  ; for each point, the letter specifies the constellation (of those in Figure 2) typically obtained.
; for each point, the letter specifies the constellation (of those in Figure 2) typically obtained.
In the next experiments, we have addressed the constellation optimization when  ; more specifically, in Figures 4 and 5 we have considered the transmission over
; more specifically, in Figures 4 and 5 we have considered the transmission over  when
when  and
and  , respectively. Figure 4 reports the SER achieved by both the suboptimum strategy and the optimum strategy versus
, respectively. Figure 4 reports the SER achieved by both the suboptimum strategy and the optimum strategy versus  for
for  and
and  . The optimum strategy provides performance gain over the non-adaptive transceiver employing the conventional rectangular 8-QAM by using the "1-7" 8-QAM and the noncircular 8-QAM for smaller values of
. The optimum strategy provides performance gain over the non-adaptive transceiver employing the conventional rectangular 8-QAM by using the "1-7" 8-QAM and the noncircular 8-QAM for smaller values of  , and, as
, and, as  , by using the 8-PAM. In such a case, the performance difference between the suboptimum strategy and the optimum one is important, especially for large values of
, by using the 8-PAM. In such a case, the performance difference between the suboptimum strategy and the optimum one is important, especially for large values of  , since the suboptimum one employs the non-uniform 8-PAM. Such a result was expected since, when
, since the suboptimum one employs the non-uniform 8-PAM. Such a result was expected since, when  increases, the optimum strategy can exploit a number of degrees of freedom significantly larger than the suboptimum strategy.
increases, the optimum strategy can exploit a number of degrees of freedom significantly larger than the suboptimum strategy.
Constellation optimization for K=8 over fixed channel  ; for each point, the letter specifies the constellation (of those in Figure 2) typically obtained.
; for each point, the letter specifies the constellation (of those in Figure 2) typically obtained.
Constellation optimization for K=8 over fixed channel  ; for each point, the letter specifies the constellation (of those in Figure 2) typically obtained.
; for each point, the letter specifies the constellation (of those in Figure 2) typically obtained.
Finally, we observe that, when  , an architecture switching between the
, an architecture switching between the  -QAM and the
-QAM and the  -PAM can provide a good trade-off between performance and complexity. Instead, when
-PAM can provide a good trade-off between performance and complexity. Instead, when  , the transceiver should switch among the Foschini&All, the noncircular
, the transceiver should switch among the Foschini&All, the noncircular  -QAM and the
-QAM and the  -PAM.
-PAM.
4.2. Random Channel
In the following simulations, we assume that  the channel has memory
the channel has memory  and its taps
and its taps  are randomly generated according to a complex-valued circularly-symmetric zero-mean white Gaussian process with unit variance (i.e.,
are randomly generated according to a complex-valued circularly-symmetric zero-mean white Gaussian process with unit variance (i.e.,  and
and  );
);  the WL MMSE equalizer has
the WL MMSE equalizer has  taps;
taps;  the results have been averaged over 500 independent channel realizations. We compare the performances achieved by four architectures: (I) the OPTimum-based architecture (OPT-based) that selects
the results have been averaged over 500 independent channel realizations. We compare the performances achieved by four architectures: (I) the OPTimum-based architecture (OPT-based) that selects  and
and  in order to minimize the symbol error rate (i.e.,
in order to minimize the symbol error rate (i.e.,  , instead of
, instead of  ); (II) the QAM-based architecture adopting the conventional circularly symmetric 4-QAM constellation; (III) the PAM-based architecture utilizing the conventional rotationally variant 4-PAM (
); (II) the QAM-based architecture adopting the conventional circularly symmetric 4-QAM constellation; (III) the PAM-based architecture utilizing the conventional rotationally variant 4-PAM ( which corresponds to the maximum WL gain); (IV) the two-choice-based architecture that switches between the 4-QAM and the 4-PAM constellations according to (27). For clarity, we point out that the solution of (26) loses about 0.3
which corresponds to the maximum WL gain); (IV) the two-choice-based architecture that switches between the 4-QAM and the 4-PAM constellations according to (27). For clarity, we point out that the solution of (26) loses about 0.3 in comparison with the OPT-based one; we consider the OPT-based architecture in order to provide a lower bound to the SER. The OPT-based and the two-choice-based architectures, unlike the QAM-based and the PAM-based ones, require the existence of a feedback channel between the receiver and the transmitter for constellation adaptation; however, the two-choice-based architecture only needs to transmit a binary information on such feedback channel.
in comparison with the OPT-based one; we consider the OPT-based architecture in order to provide a lower bound to the SER. The OPT-based and the two-choice-based architectures, unlike the QAM-based and the PAM-based ones, require the existence of a feedback channel between the receiver and the transmitter for constellation adaptation; however, the two-choice-based architecture only needs to transmit a binary information on such feedback channel.
In Figure 6, the SERs of the considered architectures are plotted versus the  (in dB). The OPT-based architecture outperforms all the others and provides an SNR-gain over the nonoptimized architectures of almost
(in dB). The OPT-based architecture outperforms all the others and provides an SNR-gain over the nonoptimized architectures of almost  for a
for a  . Interestingly, the two-choice-based architecture performs well loosing only
. Interestingly, the two-choice-based architecture performs well loosing only  in comparison with the OPT-based one. Let us also note that the PAM-based architecture performs poorly for low
in comparison with the OPT-based one. Let us also note that the PAM-based architecture performs poorly for low  , but, as the
, but, as the  increases, it outperforms the QAM-based one.
increases, it outperforms the QAM-based one.
In the next experiment, we compare the considered architectures by evaluating their capability to guarantee the required quality of service (QoS). More specifically, in Table 1, we report the percentages of the channels over which the SNR required to achieve the target SER (assumed to be  ,
,  ,
,  ) is not larger than 21
) is not larger than 21 . Moreover, Figure 7 reports the probability, say
. Moreover, Figure 7 reports the probability, say  , that each architecture loses
, that each architecture loses  in comparison with the OPT-based one for a given target SER under the condition that the SNR is not larger than 21
in comparison with the OPT-based one for a given target SER under the condition that the SNR is not larger than 21 .
.
The results show the following:
-
(i)
The PAM-based architecture is robust with respect to the communication environment since it often achieves the target SER. This is mainly due to the improved capabilities of the WL equalizer when the transmitted and the received signals are rotationally variant. However, it requires a larger
 in comparison with the OPT-based architecture to compensate for the reduction of the dimension of the signal space. Note also that such an SNR loss, which is uniformly distributed between 0
in comparison with the OPT-based architecture to compensate for the reduction of the dimension of the signal space. Note also that such an SNR loss, which is uniformly distributed between 0 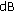 and 4
and 4 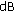 when the target SER is
when the target SER is 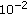 and
and  , assumes often two specific values (0
, assumes often two specific values (0  and 3
and 3 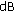 ) for a target SER equal to
) for a target SER equal to 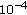 . In practice, the PAM architecture achieves optimum performance on 50
. In practice, the PAM architecture achieves optimum performance on 50 of the channels where the linear equalizer performs unsatisfactorily and the WL processing gain, specific to rotationally variant constellations, compensates for the smaller minimum-distance of the PAM constellation.
of the channels where the linear equalizer performs unsatisfactorily and the WL processing gain, specific to rotationally variant constellations, compensates for the smaller minimum-distance of the PAM constellation. -
(ii)
The QAM-based architecture is not robust with respect to the communication environment. When it is able to achieve the target SER, it requires a limited amount of excess SNR over the OPT-based architecture; nevertheless, it is unable to achieve the target SER of
 on 37
on 37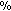 of the channels. This is due to the circular symmetry of the constellation that does not allow one to improve by means of the WL processing the unsatisfactory performance of the linear equalizer.
of the channels. This is due to the circular symmetry of the constellation that does not allow one to improve by means of the WL processing the unsatisfactory performance of the linear equalizer. -
(iii)
The two-choice-based architecture is particularly simple and robust since it combines the advantages of both PAM and QAM constellations.
5. Conclusions
We have addressed the problem of constellation optimization for the WL MMSE equalizer. By modeling the residual disturbance at the output of the WL equalizer as a white Gaussian (possibly rotationally variant) process, we have singled out constellation-design methods which minimize an upper bound of the symbol error rate. The first method exploits all the degrees of freedom ( ) associated to the
) associated to the  -order constellation exhibiting, therefore, an unaffordable computational complexity for high-order constellations. To overcome such a problem, a second design method based on a rhombic transformation of a fixed alphabet of order
-order constellation exhibiting, therefore, an unaffordable computational complexity for high-order constellations. To overcome such a problem, a second design method based on a rhombic transformation of a fixed alphabet of order  is proposed. It performs the optimization of only two parameters (instead of
is proposed. It performs the optimization of only two parameters (instead of  ) leading to a huge reduction of the computational complexity for large
) leading to a huge reduction of the computational complexity for large  . For low-order constellations, the simulation results show that the two techniques are practically equivalent in terms of symbol error rate; moreover, they also show that a WL MMSE transceiver with constellation adaptation is clearly superior to the same equalizer with fixed constellation. Finally, for
. For low-order constellations, the simulation results show that the two techniques are practically equivalent in terms of symbol error rate; moreover, they also show that a WL MMSE transceiver with constellation adaptation is clearly superior to the same equalizer with fixed constellation. Finally, for  , it has been shown that the method that switches between a real-valued and a complex-valued constellation exhibits a limited performance loss versus the optimum adaptation scheme, while it achieves a strong reduction of the computational complexity and it requires to feed back to the transmitter only a binary information.
, it has been shown that the method that switches between a real-valued and a complex-valued constellation exhibits a limited performance loss versus the optimum adaptation scheme, while it achieves a strong reduction of the computational complexity and it requires to feed back to the transmitter only a binary information.
References
Lucky R, Hancock J: On the optimum performance of N-ary systems having two degrees of freedom. IRE Transactions on Communications Systems 1962, 10: 185-192.
Foschini GJ, Gitlin RD, Weinstein SB: Optimization of two-dimensional signal constellations in the presence of Gaussian noise. IEEE Transactions on Communications 1974, 22(1):28-38. 10.1109/TCOM.1974.1092061
Chevalier P, Pipon F: New insights into optimal widely linear array receivers for the demodulation of BPSK, MSK, and GMSK signals corrupted by noncircular interferences—application to SAIC. IEEE Transactions on Signal Processing 2006, 54(3):870-883.
Palomar DP, Cioffi JM, Lagunas MA: Joint Tx-Rx beamforming design for multicarrier MIMO channels: a unified framework for convex optimization. IEEE Transactions on Signal Processing 2003, 51(9):2381-2401. 10.1109/TSP.2003.815393
Xu F, Davidson TN, Zhang J-K, Wong KM: Design of block transceivers with decision feedback detection. IEEE Transactions on Signal Processing 2006, 54(3):965-978.
Jiang Y, Li J, Hager WW: Uniform channel decomposition for MIMO communications. IEEE Transactions on Signal Processing 2005, 53(11):4283-4294.
Scaglione A, Stoica P, Barbarossa S, Giannakis GB, Sampath H: Optimal designs for space-time linear precoders and decoders. IEEE Transactions on Signal Processing 2002, 50(5):1051-1064. 10.1109/78.995062
Picinbono B: On circularity. IEEE Transactions on Signal Processing 1994, 42(12):3473-3482. 10.1109/78.340781
Kuchi K, Prabhu VK: Interference cancellation enhancement through generalized widely linear equalization in QAM systems. IEEE Transactions on Wireless Communications 2009, 8(4):1585-1590.
Picinbono B, Chevalier P: Widely linear estimation with complex data. IEEE Transactions on Signal Processing 1995, 43(8):2030-2033. 10.1109/78.403373
Kuchi K, Prabhu VK: Performance evaluation for widely linear demodulation of PAM/QAM signals in the presence of Rayleigh fading and co-channel interference. IEEE Transactions on Communications 2009, 57(1):183-193.
Gerstacker WH, Schober R, Lampe A: Equalization with widely linear filtering. Proceedings of the IEEE International Symposium on Information Theory (ISIT '01), June 2001 265.
Mirbagheri A, Plataniotis KN, Pasupathy S: An enhanced widely linear CDMA receiver with OQPSK modulation. IEEE Transactions on Communications 2006, 54(2):261-272.
Parihar A, Lampe L, Schober R, Leung C: Equalization for DS-UWB systems—part II: 4BOK modulation. IEEE Transactions on Communications 2007, 55(8):1525-1535.
Gelli G, Paura L, Ragozini ARP: Blind widely linear multiuser detection. IEEE Communications Letters 2000, 4(6):187-189. 10.1109/4234.848408
Gerstacker WH, Schober R, Lampe A: Receivers with widely linear processing for frequency-selective channels. IEEE Transactions on Communications 2003, 51(9):1512-1523. 10.1109/TCOMM.2003.816992
Parihar A, Lampe L, Schober R, Leung C: Equalization for DS-UWB systems—part I: BPSK modulation. IEEE Transactions on Communications 2007, 55(6):1164-1173.
Mattera D, Paura L, Sterle F: Widely linear MMSE equaliser for MIMO linear time-dispersive channel. Electronics Letters 2003, 39(20):1481-1482. 10.1049/el:20030945
Lampe A, Breiling M: Asymptotic analysis of widely linear MMSE multiuser detection-complex vs real modulation. Proceedings of the IEEE Information Theory Workshop, September 2001 55-57.
Anderson JB: Digital Transmission Engineering. 2nd edition. IEEE Press, New York, NY, USA; 2005.
Lin Y-P, Phoong S-M: Optimal ISI-free DMT transceivers for distorted channels with colored noise. IEEE Transactions on Signal Processing 2001, 49(11):2702-2712. 10.1109/78.960417
Palomar DP, Barbarossa S: Designing MIMO communication systems: constellation choice and linear transceiver design. IEEE Transactions on Signal Processing 2005, 53(10):3804-3818.
Makowski AM: On the optimality of uniform pulse amplitude modulation. IEEE Transactions on Information Theory 2006, 52(12):5546-5549.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lipardi, M., Mattera, D. & Sterle, F. Constellation Design for Widely Linear Transceivers. EURASIP J. Adv. Signal Process. 2010, 176587 (2010). https://doi.org/10.1155/2010/176587
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/176587

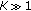 ; in fact, the SER becomes a function of only two variables (
; in fact, the SER becomes a function of only two variables ( and
and  ), regardless of the constellation order
), regardless of the constellation order 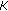 ;
; ) have to be sent to the transmitter.
) have to be sent to the transmitter.





 in comparison with the OPT-based architecture to compensate for the reduction of the dimension of the signal space. Note also that such an SNR loss, which is uniformly distributed between 0
in comparison with the OPT-based architecture to compensate for the reduction of the dimension of the signal space. Note also that such an SNR loss, which is uniformly distributed between 0 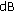 and 4
and 4 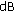 when the target SER is
when the target SER is 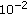 and
and  , assumes often two specific values (0
, assumes often two specific values (0  and 3
and 3 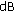 ) for a target SER equal to
) for a target SER equal to 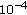 . In practice, the PAM architecture achieves optimum performance on 50
. In practice, the PAM architecture achieves optimum performance on 50 of the channels where the linear equalizer performs unsatisfactorily and the WL processing gain, specific to rotationally variant constellations, compensates for the smaller minimum-distance of the PAM constellation.
of the channels where the linear equalizer performs unsatisfactorily and the WL processing gain, specific to rotationally variant constellations, compensates for the smaller minimum-distance of the PAM constellation. on 37
on 37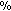 of the channels. This is due to the circular symmetry of the constellation that does not allow one to improve by means of the WL processing the unsatisfactory performance of the linear equalizer.
of the channels. This is due to the circular symmetry of the constellation that does not allow one to improve by means of the WL processing the unsatisfactory performance of the linear equalizer.