- Research Article
- Open access
- Published:
Modeling of Video Sequences by Gaussian Mixture: Application in Motion Estimation by Block Matching Method
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 210937 (2010)
Abstract
This article investigates a new method of motion estimation based on block matching criterion through the modeling of image blocks by a mixture of two and three Gaussian distributions. Mixture parameters (weights, means vectors, and covariance matrices) are estimated by the Expectation Maximization algorithm (EM) which maximizes the log-likelihood criterion. The similarity between a block in the current image and the more resembling one in a search window on the reference image is measured by the minimization of Extended Mahalanobis distance between the clusters of mixture. Performed experiments on sequences of real images have given good results, and PSNR reached 3 dB.
1. Introduction
Motion estimation is the process which generates the motion vectors that determines how each motion compensated prediction frame is created from the previous frame. It examines the movement of objects in an image sequence to try to obtain vectors representing the estimated motion. Motion compensation uses the knowledge of object motion obtained to achieve data compression.
Motion estimation plays a key role in many video applications, such as frame-rate video conversion, video retrieval, video surveillance, and video compression.
The key issue in these applications is to define appropriate representations that can efficiently support motion estimation with the required accuracy.
In interframe coding, motion estimation and compensation have become powerful techniques to eliminate the temporal redundancy due to high correlation between consecutive frames [1].
In real video scenes, motion can be a complex combination of translation and rotation. Such motion is difficult to estimate and may require large amounts of processing. However, translational motion is easily estimated and has been used successfully for motion compensated coding. Most of the motion estimation algorithms make the following assumptions [2–4].
-
(1)
Objects move in translation in a parallel plane to the camera plane, that is, the effects of camera zoom and object rotations are not considered.
-
(2)
Illumination is spatially and temporally uniform.
-
(3)
Occlusion of one object by another and uncovered background are neglected.
Several motion estimation approaches have been proposed so far in the open literature such as pel-recursive algorithms, frequency domain techniques, optical flow, and block matching methods.
Pel-recursive Algorithms rely on iterative refining of motion estimation for individual pels by gradient methods that enable to predict recursively the displacement of each pel from its neighbouring pels. These algorithms involve more computational complexity and less regularity and are therefore difficult to realize in hardware [5]. Frequency motion estimation techniques are mainly used for the global motion estimation. The most known frequency technique is the phase correlation method that capitalizes on the well-known Fourier shift theorem which states that shifts in the spatial domain correspond to linear phase changes in the Fourier domain [6–8]. Optical flow estimation ensures high accuracy for scenes with small displacements but fails when the displacements are large. In general, these methods suffer from the aperture problem because each neighbourhood of pixels can have a different motion in the image [9–11]. Block Matching Algorithms estimate motion on the basis of rectangular blocks and produce one motion vector for each block. These algorithms are more suitable for a simple hardware realization because of their regularity and simplicity [12].
Figure 1 illustrates a process of block matching algorithm BMA. In a typical BMA, each frame is divided into blocks, each one of them consists of luminance and chrominance blocks. Usually, for coding efficiency, motion estimation is performed only on the luminance block. Each luminance block in the present frame is matched against candidate blocks in a search area on the reference frame. These candidate blocks are just the displaced versions of the original block. The best (least distorted, i.e., most matched) candidate block is found, and its displacement (motion vector) is recorded. In a typical interframe coder, the input frame is subtracted from the prediction of the reference frame. Consequently the motion vector and the resulting error can be transmitted instead of the original luminance block; thus, interframe redundancy is removed and data compression is achieved. At the receiver end, the decoder builds the frame difference signal from the received data and adds it to the reconstructed reference frames. The summation gives an exact replica of the current frame. The better the prediction, the smaller the error signal and hence the transmission bit rate [13]. Despite the success of block matching standards method, these techniques are only based on the luminosity, and one can find misleading cases where the hypothesis of constant levels of gray is not verified. Some models take into account a factor of change of brightness in the scene. Thus the change in brightness is supposed to offset during the estimation. Such adjustments can improve the result of global changes in brightness, for which it is possible to estimate the change in a reliable manner, as against it does not take into account local variations, such as shadows. Therefore, we propose a statistical method to estimate the motion based on modeling image blocks by a mixture of Gaussian distributions. These mixtures are robust, relatively easy to use, and have traditionally learned independently, class by class, using a criterion of maximum likelihood [14–16]. The optimization is then performed using the algorithm EM (Expectation-Maximization) based on an iterative optimization of the model parameters (a priori probability, vectors means, and covariances matrices). Then we resort to the Extended Mahalanobis distances to measure the similarity and to search for the best matching between two windows spaces (or blocks) located in consecutive frames.
This paper is organized as follows. In Section 2, the modeling and parameter estimation of Gaussian mixtures is briefly described. The distance measure between Gaussian mixtures models is studied in Section 3. We describe our approach in Section 4. Section 5 presents simulation results under and without influence of noise. Some concluding remarks are given in Section 6.
2. Modeling and Parameter Estimation of Gaussian Mixtures
We consider the following Gaussian mixture model [17]

where k is the number of components in the mixture, ( are the mixing proportions of components satisfying
are the mixing proportions of components satisfying  , and each component density
, and each component density  is a Gaussian probability density function given by
is a Gaussian probability density function given by

where n is the dimensionality of the vector x,  is the mean vector, and
is the mean vector, and  is the covariance matrix assumed to be positive definite. For clarity, we let
is the covariance matrix assumed to be positive definite. For clarity, we let  be the collection of all the parameters in the mixture, that is,
be the collection of all the parameters in the mixture, that is, 
Given a set of  i.i.d. samples,
i.i.d. samples,  , the log-likelihood function for the Gaussian mixture model is expressed as follows:
, the log-likelihood function for the Gaussian mixture model is expressed as follows:

which can be maximized to get a Maximum Likelihood (ML) [18] estimate of  via the following EM algorithm:
via the following EM algorithm:

where  are the posterior probabilities.
are the posterior probabilities.
As EM is highly dependent on initialization, the first set of parameters selection is very important for EM algorithm. If the initial parameters are not well selected, the algorithm may converge into local maxima points. The convergence properties of EM algorithm over Gaussian Mixture Model have been extensively studied in [19, 20].
3. Distance Measures between Gaussian Mixtures Models
Popular distance measures from the field of statistics include the Kullback-Leibler divergence and the Extended Mahalanobis distance. The Kullback-Leibler divergence can be seen as a dissimilarity measure between two probability functions. However, it is not symmetric and does not obey the triangle inequality and is thus not a true metric. The Extended Mahalanobis distance metric can be extended to a distance measure between two distributions by combining the covariance matrices of the distributions [21]. We have no prior preference for any of these two distances; they give almost the same results, which is based on the statistical distribution of data and not on data directly. The advantage of the Extended Mahalanobis distance relies on the fact that it is easy to calculate. In practice, in the case of two Gaussian distributions  and
and  the measure between two means vectors is defined as follows:
the measure between two means vectors is defined as follows:

However, this measure creates a singularity for singular covariance matrices. In practical problems it often appears in learning such models mixture. The acquired covariance matrix are not always conditioned and their inversion creates a problem. In our implementation, we replace the inverse of singular covariance matrix by its pseudoinverse. Singular value decomposition is used for the calculation of the pseudoinverse. Roundoff errors can lead to a singular value not being exactly zero even if it should be. Tolerance parameter places a threshold when comparing singular values with zero and improves the numerical stability of the method with singular or near-singular matrices.
4. Approach and Conception of the Proposed Method
Considering a video sequence containing moving objects, we estimate the displacement vector of each object in the image plane by the technique of Full Search Block Matching Algorithm. The current frame is divided into a matrix of "macro-blocks" that are then compared with the corresponding block and its adjacent neighbours in the previous frame. This enables to create a vector that stipulates the movement of a macro-block from one location to another in the previous frame. This movement, calculated for all the macro-blocks included in a frame, represents the motion estimated in the current frame. The search area for a good macro-block match is constrained up to p pixels on all fours sides of the corresponding macro-block in the previous frame. This " " stands for the search parameter. Larger motions require a larger
" stands for the search parameter. Larger motions require a larger  ; the larger the search parameter is, the more computationally expensive the process of motion estimation becomes. The idea is depicted in Figure 2. The matching of one macro-block with another is based on the output of a cost function. The macro-block that results in the least cost is the one that closely matches to current block [22, 23].
; the larger the search parameter is, the more computationally expensive the process of motion estimation becomes. The idea is depicted in Figure 2. The matching of one macro-block with another is based on the output of a cost function. The macro-block that results in the least cost is the one that closely matches to current block [22, 23].
4.1. The Cost Function
The cost function is defined by Extended Mahalanobis distance weighted by the weight of Gaussian distributions components. This distance is applied between the following components: Gaussian interblocks (reference/Current), the components of strong weights, the components of medium weights, and the components of weak weights (Figure 3).
The distances  ,
,  and
and  are defined as follows:
are defined as follows:

When modeling by a mixture of two Gaussian distributions, the cost function is defined by the Extended Mahalanobis distance between the components of strong weights  and the components of weak weights
and the components of weak weights  .
.
4.2. Steps of the Proposed Method
The proposed method is based on three steps design.
-
(1)
Each block in the reference image or the current image is modeled by a mixture of three Gaussian distributions. This modeling consists in estimating the parameters of the mixture (weight, means vectors, and covariance matrix).
-
(2)
The Parameters are sorted based on their weights in mixture. This allows the identification of the components of weak weights, the components of medium weights, and the components of strong weights.

-
(3)
Research of minimal interblocks distance (reference/current).
-
(a)
The Extended Mahalanobis distances between a block of the current image and all blocks in a search window
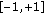 in the reference image are stored in the matrices
in the reference image are stored in the matrices 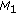 ,
,  , and
, and 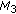 .
.-
(M1) matrix contains the values of Extended Mahalanobis distances between the components of weak weights.
-
(M2) matrix contains the values of Extended Mahalanobis distances between the components of medium weights.
-
(M3) matrix contains the values of Extended Mahalanobis distances between the components of strong weights.
-
-
(b)
The value of the minimal distance of the three matrices
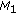 ,
, 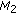 , and
, and  corresponds to the most similar block in reference image.
corresponds to the most similar block in reference image.
-
(a)
4.3. Practical Considerations
Matrices  ,
,  , and
, and  show the Extended Mahalanobis distances between a block of the current image and all blocks in a search window
show the Extended Mahalanobis distances between a block of the current image and all blocks in a search window  in the reference image of the Foreman sequence.
in the reference image of the Foreman sequence.
Matrix  contains the distances between the components of weak weights.
contains the distances between the components of weak weights.
Matrix  contains the distances between the components of medium weights.
contains the distances between the components of medium weights.
Matrix  contains the distances between the components of strong weights.
contains the distances between the components of strong weights.
The value of the minimum distance of the three matrices  ,
,  , and
, and  is equal to 0.93 corresponding to the first line second column indices in the matrix
is equal to 0.93 corresponding to the first line second column indices in the matrix  . These indices correspond to the most similar blocks in the reference image.
. These indices correspond to the most similar blocks in the reference image.
For these types of Foreman sequence, about 80% minimum distances are in the matrix  (distances between the components of weak weights). This percentage mainly depends on statistical characteristics of pixels in the image.
(distances between the components of weak weights). This percentage mainly depends on statistical characteristics of pixels in the image.
5. Experimental Results
The parameters of motion estimation used for comparing and evaluating the quality of the obtained results from our proposed methods are as follows.
-
(i)
Method: exhaustive block-matching (full search) is the most obvious candidate for a search technique for finding the best possible weight in the search area.
-
(ii)
Classical criterion methods.
-
(a)
Sum of Absolute Differences "SAD".
-
(b)
Sum of Square Error "SSE".
-
(c)
Normalized Cross-Correlation "NCC".
-
(a)
-
(iii)
Method proposed criterion: minimization of Extended Mahalanobis distance between mixture of two and three Gaussian distributions ("GMM2" and "GMM3").
-
(iv)
Precision: pixel.
-
(v)
Block Size:
 .
. -
(vi)
Search area:
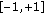 .
.
5.1. Simulation Results without Noise Influence
5.1.1. Objective Evaluation
The proposed approach was evaluated by using a standard measure, the average PSNR (Peak Signal to Noise Ratio), given as

where  is the measured PSNR for frame
is the measured PSNR for frame  , and
, and  is the total number of frames. We will compare the "GMM3" and "GMM2" methods against the "SAD", "SSE", and "NCC" methods. In addition, the PSNR comparison among the five algorithms will be introduced.
is the total number of frames. We will compare the "GMM3" and "GMM2" methods against the "SAD", "SSE", and "NCC" methods. In addition, the PSNR comparison among the five algorithms will be introduced.
As an example, Table 4 shows that six test image sequences have different characteristics. While "Foreman" represents the characteristics of slow motion image sequences, "Hand" and "Soccer" are fast motion image sequences, "coastguard" is global motion image sequence, and Football and Cones contain multiple objects moving. Table 4 shows that the performance of "GMM3" and GMM2 methods are better than "SAD", "SSE", and "NCC" methods for the test video sequences.
 .
. .
. .
.Another performance comparison is made among the first 15 frames of each sequence. As an example, Figures 4 and 5 show the performance comparison for the first 15 frames of "Soccer" and "Cones" sequences. The PSNR comparison shows that the "GMM3" and "GMM2" usually perform better than the "SAD", "SSE", and "NCC" algorithms.
5.1.2. Subjective Evaluation
To demonstrate the performance of our algorithm, we applied the new methods of motion estimation ("GMM2" and "GMM3") on the "soccer" sequences (Figure 6). The players shadows (Figure 6(c)) and (Figure 6(d)) are better estimated by the methods "GMM2" and "GMM3" compared to the ones estimated by the method "SSE" (Figure 6(b)).
5.2. Simulation Results under Influence of Noise
Additive Gaussian noise with standard deviation equal to 10 and Uniform noise with standard deviation equal to 20 degraded the video sequences. We applied the motion estimation algorithms "SAD", "SSE", "NCC", "GMM2", and "GMM3" on Soccer and Cones sequences. The results are summarized in Figures 7 and 8.
6. Conclusion and Perspective
In this paper we have modeled sequence images blocks by a mixture of two and three Gaussian distributions and have used block matching criterion based on Mahalanobis distance minimization between the clusters of mixture to estimate motion. This technique has been compared to other equivalent methods in the literature. The simulation confirms that the proposed technique allows the significant PSNR gains. These gains can be observed in terms of both the perceptual quality and the PSNR of the restored images. However, this technique requires more computations. It might be necessary to further reduce computations to fit real time requirements. Parameters estimation of Gaussian mixture consists of repetitive operations which could greatly benefit from some existing architectures to perform repetitive tasks efficiently. A forthcoming work will be devoted to improve the speed of execution and further increase performance by modeling the blocks of the image by a Gaussian mixture where the number of clusters varies.
References
Lucas B, Kanade T: An iterative image registration technique with an application to stereo vision. Proceedings of the DARPA Image Understanding Workshop, 1981 121-130.
Dufaux F, Moscheni F: Motion estimation techniques for digital TV: a review and a new contribution. Proceedings of IEEE 1995, 83(6):858-876. 10.1109/5.387089
Tziritas G, Labit C: Motion analysis for image sequence coding. In Advances in Image Communication. Volume 4. Elsevier, Amsterdam, The Netherlands; 1994.
Stiller C, Konrad J: Estimating motion in image sequences, a tutorial on modeling and computation of 2D motion. IEEE Signal Processing Magazine 1999, 16(4):70-91. 10.1109/79.774934
Estrela V, Rivera LA, Beggio PC, Lopes RT: Regularized pel-recursive motion estimation using generalized cross-validation and spatial adaptation. Proceedings of the 16th Brazilian Symposium on Computer Graphics and Image Processing (SIBGRAPI '03), 2003 331-338.
Argyriou V, Vlachos T: Performance study of gradient correlation for sub-pixel motion estimation in the frequency domain. IEE Proceedings: Vision, Image and Signal Processing 2005, 152(1):107-114. 10.1049/ip-vis:20051073
Ertürk S: Digital image stabilization with sub-image phase correlation based global motion estimation. IEEE Transactions on Consumer Electronics 2003, 49(4):1320-1325. 10.1109/TCE.2003.1261235
Essannouni F, Oulad Haj Thami R, Salam A, Aboutajdine D: A new fast full search block matching algorithm using frequency domain. Proceedings of the 8th International Symposium on Signal Processing and Its Applications (ISSPA '05), 2005 2: 559-562.
Heeger DJ: Optical flow using spatiotemporal filters. Proceedings of the 1st International Conference on Computer Vision, 1988 181-190.
Alvarez L, Weickert J, Sánchez J: Reliable estimation of dense optical flow fields with large displacements. International Journal of Computer Vision 2000, 39(1):41-56. 10.1023/A:1008170101536
Jacobson L, Wechsler H: Derivation of optical flow using a spatiotemporal-frequency approach. Computer Vision, Graphics, & Image Processing 1987, 38(1):29-65. 10.1016/S0734-189X(87)80152-4
Zhu C, Qi W-S, Ser W: A new successive elimination algorithm for fast block matching in motion estimation. Proceedings of the IEEE International Symposium on Circuits and Systems (ISCAS '04), 2004 3: 733-736.
Xu J-B, Po L-M, Cheung C-K: Adaptive motion tracking block matching algorithms for video coding. IEEE Transactions on Circuits and Systems for Video Technology 1999, 9(7):1025-1029. 10.1109/76.795056
Dempster AP, Laird NM, Rubin DB: Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical, Series B 1977, 39: 1-38.
Neal R, Hinton G: A view of the em algorithm that justifies incremental, sparse, and other variants. In Learning in Graphical Models. Edited by: Jordan MI. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1998.
Afify M: Extended baum-welch reestimation of Gaussian mixture models based on reverse jensen inequality. Proceedings of the 9th European Conference on Speech Communication and Technology, 2005 1113-1116.
McLachlan GJ, Peel D: Finite Mixture Models. John Wiley & Sons, New York, NY, USA; 2000.
Sanjay-Gopal S, Hebert TJ: Bayesian pixel classification using spatially variant finite mixtures and the generalized EM algorithm. IEEE Transactions on Image Processing 1998, 7(7):1014-1028. 10.1109/83.701161
Redner RA, Walker HF: Mixture densities, maximum likelihood and the EM algorithm. SIAM Review 1984, 26(2):195-239. 10.1137/1026034
Xu L, Jordan MI: On convergence properties of the EM algorithm for Gaussian mixtures. Neural Computation 1996, 8(1):129-151. 10.1162/neco.1996.8.1.129
Younis K, Karim M, Hardie R, Loomis J, Rogers S, DeSimio M: Cluster merging based on weighted Mahalanobis distance with application in digital mammography. Proceedings of the IEEE National Aerospace and Electronics Conference (NAECON '98), July 1998 525-530.
Packwood RA, Steliaros MK, Martin GR: Variable size block matching motion compensation for object-based video coding. Proceedings of the 6th IEE International Conference on Image Processing & Its Applications, July 1997, Dublin, Ireland 56-60.
Barjatya A: Block matching algorithms for motion estimation. IEEE Transactions Evolution Computation 2004, 8(3):225-239. 10.1109/TEVC.2004.826069
Acknowledgments
The authors would like to thank Mohamed Zyoute, Fatima Boudlal, Fadoua Ataa-Allah Nizar Bennani, and Hatim Chergui for their help.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Boudlal, A., Nsiri, B. & Aboutajdine, D. Modeling of Video Sequences by Gaussian Mixture: Application in Motion Estimation by Block Matching Method. EURASIP J. Adv. Signal Process. 2010, 210937 (2010). https://doi.org/10.1155/2010/210937
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/210937



 , the components of medium weights
, the components of medium weights  , and the components of weak weights
, and the components of weak weights  .
.
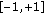 in the reference image are stored in the matrices
in the reference image are stored in the matrices 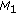 ,
,  , and
, and 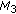 .
.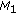 ,
, 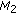 , and
, and  corresponds to the most similar block in reference image.
corresponds to the most similar block in reference image. .
. .
.



