- Research Article
- Open access
- Published:
Progressive Exponential Clustering-Based Steganography
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 212517 (2010)
Abstract
Cluster indexing-based steganography is an important branch of data-hiding techniques. Such schemes normally achieve good balance between high embedding capacity and low embedding distortion. However, most cluster indexing-based steganographic schemes utilise less efficient clustering algorithms for embedding data, which causes redundancy and leaves room for increasing the embedding capacity further. In this paper, a new clustering algorithm, called progressive exponential clustering (PEC), is applied to increase the embedding capacity by avoiding redundancy. Meanwhile, a cluster expansion algorithm is also developed in order to further increase the capacity without sacrificing imperceptibility.
1. Introduction
Many steganographic schemes have been developed for hiding data in vector-quantisation (VQ) compressed colour images (also called palette images) [1–14]. Although there are variations among them, a common feature of these methods is that they partition the codebook into a number of groups or clusters and then embed the secret message by replacing the codeword indices of the compressed image with those of the same group/cluster selected according to the corresponding secret data bits. For example with a cluster of 8 ( ) codewords, each codeword can embed 3 bits of the secret message. If the binary secret data bits is
) codewords, each codeword can embed 3 bits of the secret message. If the binary secret data bits is  , (or
, (or  ), the second (or sixth) codeword is used to replace the original codeword. The receiving end of the stego-image needs to have the same clustering of the same codebook. The secret message is extracted by concatenating the position/index (in binary form) of the received codewords in their groups/clusters. Therefore, we can see that the greater the cluster, the greater the embedding capacity of each codeword of the cluster [1, 4, 12]. The size of a cluster is determined by the distance between each codeword and the cluster's centroid. The greater the distance is allowed, the larger the cluster is. However, the greater a cluster is, the greater the variance among the codewords in the cluster becomes, meaning the average embedding distortion is greater because the possibility that a codeword gets replaced with a more distant codeword is higher [4, 12]. So striking a good balance between embedding capacity and embedding distortion is important, but unfortunately not trivial. The feasibility resides in the optimality of the codebook clustering algorithm [4, 12]. Because of the indexing characteristic of this type of schemes, we describe them as cluster indexing-based steganography in this paper. In Du and Hsu's work [2], the clustering algorithm treats the secret message as a clustering parameter. The value of the secret message and the size of groups from each clustering step are combined as the threshold of the clustering algorithm. As a result, when embedding different secret messages, the codebook must be reclustered. Furthermore, the performance of the method is dependent on the secret message, making the performance evaluation of the algorithm difficult. Another drawback of some schemes of this category (e.g., [1]) is that the size of each cluster is not a power of 2, making some colours in the same cluster redundant, thus reducing overall embedding capacity. For example, if the size
), the second (or sixth) codeword is used to replace the original codeword. The receiving end of the stego-image needs to have the same clustering of the same codebook. The secret message is extracted by concatenating the position/index (in binary form) of the received codewords in their groups/clusters. Therefore, we can see that the greater the cluster, the greater the embedding capacity of each codeword of the cluster [1, 4, 12]. The size of a cluster is determined by the distance between each codeword and the cluster's centroid. The greater the distance is allowed, the larger the cluster is. However, the greater a cluster is, the greater the variance among the codewords in the cluster becomes, meaning the average embedding distortion is greater because the possibility that a codeword gets replaced with a more distant codeword is higher [4, 12]. So striking a good balance between embedding capacity and embedding distortion is important, but unfortunately not trivial. The feasibility resides in the optimality of the codebook clustering algorithm [4, 12]. Because of the indexing characteristic of this type of schemes, we describe them as cluster indexing-based steganography in this paper. In Du and Hsu's work [2], the clustering algorithm treats the secret message as a clustering parameter. The value of the secret message and the size of groups from each clustering step are combined as the threshold of the clustering algorithm. As a result, when embedding different secret messages, the codebook must be reclustered. Furthermore, the performance of the method is dependent on the secret message, making the performance evaluation of the algorithm difficult. Another drawback of some schemes of this category (e.g., [1]) is that the size of each cluster is not a power of 2, making some colours in the same cluster redundant, thus reducing overall embedding capacity. For example, if the size  of a cluster
of a cluster  is not a power of 2, then
is not a power of 2, then  colours are redundant and not contributing to the improvement of embedding capacity.
colours are redundant and not contributing to the improvement of embedding capacity.
A less studied steganographic technique is the application of the aforementioned cluster indexing idea to hiding data in true colour images [15, 16] due to the fact that the size of the palette (codebook or colour table) is  , which is
, which is  times greater then that of VQ-compressed images and complicates the clustering of colours. In [16], instead of using the entire colour space with
times greater then that of VQ-compressed images and complicates the clustering of colours. In [16], instead of using the entire colour space with  colours as the codebook, a colour table containing only the colours present in the original image is first created. A
colours as the codebook, a colour table containing only the colours present in the original image is first created. A  -means clustering algorithm is then applied to cluster the colours in the colour table into
-means clustering algorithm is then applied to cluster the colours in the colour table into  clusters/groups. Thirdly, the entire colour space with
clusters/groups. Thirdly, the entire colour space with  colours is partitioned into
colours is partitioned into  cubes, with each cube centred at one centroid of the
cubes, with each cube centred at one centroid of the  clusters formed in the first step. Subsequently, each cube is reduced to a 3-dimensional sphere containing
clusters formed in the first step. Subsequently, each cube is reduced to a 3-dimensional sphere containing  colours, where
colours, where  is a prespecified parameter which determines the capacity and distortion of the scheme. Finally, to embed data bits with a value equal to
is a prespecified parameter which determines the capacity and distortion of the scheme. Finally, to embed data bits with a value equal to  into a pixel, the algorithm identifies the cluster which contains the colour of the pixel and then replaces the colour with the
into a pixel, the algorithm identifies the cluster which contains the colour of the pixel and then replaces the colour with the  th colour in the sphere centred at the centroid of the identified clusters. To extract the secret data from the received image, an
th colour in the sphere centred at the centroid of the identified clusters. To extract the secret data from the received image, an  -element colour palette (i.e., the centroids of the same
-element colour palette (i.e., the centroids of the same  colour clusters) has to be transmitted to the recipient so that the same colour clusters can be reestablished. From each pixel, the index of the pixel's colour in its cluster is taken as the secret data bits carried by the pixel. By concatenating those colour indices, the complete secret message can be formed if the stego-image is not manipulated. Although high embedding capacity of this scheme has been reported, high distortion due to the low density of the colour clusters makes this scheme unacceptable. Based on [16], Brisbane et al. proposed another scheme [15], aiming at trading embedding capacity for embedding distortion. Although the objective of reducing embedding distortion is achieved, the same requirement of communicating the extrapalette to the receiving side stands as the main limitation on the feasibility of the scheme. For example, if
colour clusters) has to be transmitted to the recipient so that the same colour clusters can be reestablished. From each pixel, the index of the pixel's colour in its cluster is taken as the secret data bits carried by the pixel. By concatenating those colour indices, the complete secret message can be formed if the stego-image is not manipulated. Although high embedding capacity of this scheme has been reported, high distortion due to the low density of the colour clusters makes this scheme unacceptable. Based on [16], Brisbane et al. proposed another scheme [15], aiming at trading embedding capacity for embedding distortion. Although the objective of reducing embedding distortion is achieved, the same requirement of communicating the extrapalette to the receiving side stands as the main limitation on the feasibility of the scheme. For example, if  , then approximately 3,000 bytes of data have to be transmitted to the recipient. This extracommunication not only requires extraresource, but more seriously, presents a security gap for potential attack. Moreover, a common limitation of the aforementioned methods is that they are not immune to histogram analysis as we will discuss in Section 4.1.
, then approximately 3,000 bytes of data have to be transmitted to the recipient. This extracommunication not only requires extraresource, but more seriously, presents a security gap for potential attack. Moreover, a common limitation of the aforementioned methods is that they are not immune to histogram analysis as we will discuss in Section 4.1.
In this work, we propose a Progressive Exponential Clustering-(PEC-) based steganographic scheme, aiming at striking a good balance between high embedding capacity and low embedding distortion. Meanwhile, the proposed scheme does not have to transmit the palette from the embedding side to the recipient, hence strengthening security. Moreover, the proposed scheme is immune to histogram analysis [1, 15, 16].
2. Progressive Exponential Clustering- (PEC-)Based Steganography
In this section, we propose a Progressive Exponential Clustering- (PEC-) based steganographic scheme for hiding secret data in true colour images. Figure 1 illustrates the main idea of the proposed scheme. The first step of this scheme is to create a colour table  , which covers all colours present in the original image
, which covers all colours present in the original image  . In the second step, the colour table is partitioned into a number of groups using the Progressive Exponential Clustering (PEC) algorithm (to be described in Section 2.2). The result of this grouping is a set of clusters
. In the second step, the colour table is partitioned into a number of groups using the Progressive Exponential Clustering (PEC) algorithm (to be described in Section 2.2). The result of this grouping is a set of clusters  of various sizes, each containing
of various sizes, each containing  colours, where
colours, where  is a positive integer variable depending on the size of the cluster. In Step 3, each cluster is expanded by adding a number of virtual colours, which are not present in the original image and near the centroid of the cluster, in order to form an expanded cluster with
is a positive integer variable depending on the size of the cluster. In Step 3, each cluster is expanded by adding a number of virtual colours, which are not present in the original image and near the centroid of the cluster, in order to form an expanded cluster with  colour (
colour ( ). The cluster expansion operation results in an expanded colour table
). The cluster expansion operation results in an expanded colour table  . Throughout the rest of the paper, we will use the terms physical colours to represent the colours present in the original image
. Throughout the rest of the paper, we will use the terms physical colours to represent the colours present in the original image  and virtual colours to represent the added colours that are absent in the original image. The purpose of expanding the clusters is to increase the embedding capacity, and the reason of selecting the virtual colours near the centroids is to minimise the embedding distortion. Step 4 modifies the original image slightly by assigning each virtual colour to only one pixel whose physical colour is present in the same cluster as the virtual colour. The result of Step 4 is a modified image
and virtual colours to represent the added colours that are absent in the original image. The purpose of expanding the clusters is to increase the embedding capacity, and the reason of selecting the virtual colours near the centroids is to minimise the embedding distortion. Step 4 modifies the original image slightly by assigning each virtual colour to only one pixel whose physical colour is present in the same cluster as the virtual colour. The result of Step 4 is a modified image  containing all of the physical and virtual colours. The reason of doing so is to ensure that after hiding the secret data, all the physical and virtual colours will be present in the stego-image such that the recipient of the stego-image can re-establish the same colour table and cluster configuration in the data extraction process. Step 5 partitions
containing all of the physical and virtual colours. The reason of doing so is to ensure that after hiding the secret data, all the physical and virtual colours will be present in the stego-image such that the recipient of the stego-image can re-establish the same colour table and cluster configuration in the data extraction process. Step 5 partitions  using the same PEC algorithm to create a new cluster configuration
using the same PEC algorithm to create a new cluster configuration  . Because the colour table is modified by inserting virtual colours, the reclustering is necessary to ensure that the same cluster configurations are used in the embedding and extraction phase. The final step (Step 6) is to hide the secret data stream into the modified image
. Because the colour table is modified by inserting virtual colours, the reclustering is necessary to ensure that the same cluster configurations are used in the embedding and extraction phase. The final step (Step 6) is to hide the secret data stream into the modified image  based on the final clustering configuration
based on the final clustering configuration  . To embed secret data bits with a value equal to
. To embed secret data bits with a value equal to  into a pixel based on the final clustering, the cluster which contains the colour of the pixel is identified, and the colour of that pixel is replaced with the
into a pixel based on the final clustering, the cluster which contains the colour of the pixel is identified, and the colour of that pixel is replaced with the  th colour of the identified cluster. The secret data hiding process is repeated on the ensuing pixels until the entire secret data stream is embedded. The details of each main step are presented in the following subsections.
th colour of the identified cluster. The secret data hiding process is repeated on the ensuing pixels until the entire secret data stream is embedded. The details of each main step are presented in the following subsections.
2.1. Colour Table Generation
The colour table generation in Step 1 of Figure 1 is the operation of collecting, without repetition, all the colours present in the original image  in the raster scan order to create a colour table
in the raster scan order to create a colour table  . Usually images with large homogeneous areas or low-frequency components lead to a smaller colour table than those images mainly consisting of high-frequency components.
. Usually images with large homogeneous areas or low-frequency components lead to a smaller colour table than those images mainly consisting of high-frequency components.
2.2. Progressive Exponential Clustering (PEC)
In the preliminary clustering phase (step (2) of Figure 1), the colour table  is taken as the input to the proposed PEC algorithm, as presented in Algorithm 1, and the PEC algorithm randomises the orders of the colours in
is taken as the input to the proposed PEC algorithm, as presented in Algorithm 1, and the PEC algorithm randomises the orders of the colours in  under the control of a secret key
under the control of a secret key  and partitions
and partitions  into a number of clusters, each with a size equal to a power (h) of 2. The main idea of this iterative PEC algorithm is that, initially, in Iteration 0, each individual colour in the colour table
into a number of clusters, each with a size equal to a power (h) of 2. The main idea of this iterative PEC algorithm is that, initially, in Iteration 0, each individual colour in the colour table  is treated as a singleton cluster, and then a pairing operation matches each cluster to one of the clusters within a Euclidean distance of
is treated as a singleton cluster, and then a pairing operation matches each cluster to one of the clusters within a Euclidean distance of  to form a new double-sized cluster. The process repeats until no more matches can be made. The centroid/average of each cluster pair is calculated, and then, with the leftover clusters excluded, the entire new set of the paired clusters is subjected to the same pairing operation under the constraint of the same threshold
to form a new double-sized cluster. The process repeats until no more matches can be made. The centroid/average of each cluster pair is calculated, and then, with the leftover clusters excluded, the entire new set of the paired clusters is subjected to the same pairing operation under the constraint of the same threshold  in the next iteration. The pairing/clustering operation iterates progressively until no match is made throughout an entire iteration. The final clustering is achieved by concatenating the leftover clusters of all iterations. The reason we want the size of each cluster to be equal to a power of 2 is to eliminate redundancy so as to increase the overall embedding capacity.
in the next iteration. The pairing/clustering operation iterates progressively until no match is made throughout an entire iteration. The final clustering is achieved by concatenating the leftover clusters of all iterations. The reason we want the size of each cluster to be equal to a power of 2 is to eliminate redundancy so as to increase the overall embedding capacity.
Algorithm 1: Progressive exponential clustering (PEC) algorithm.
Input: colour table  , Euclidean distance
, Euclidean distance  , secret key
, secret key 
Output: cluster configuration 
PEC algorithm
-
(1)
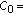 The set of colours in
The set of colours in 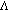 with their orders randomised according to secret key
with their orders randomised according to secret key 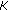 (each individual colour is seen as a cluster);
(each individual colour is seen as a cluster); -
(2)
 ;
; -
(3)
clustering_completed:= FALSE;
-
(4)
While clustering_completed:= FALSE;
-
(4.1)
Calculate the centroid
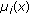 of each cluster
of each cluster 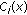 in
in  ;
; -
(4.2)
 ;
; -
(4.3)
For every
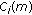 in
in 
-
(4.3.1)
For
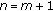 to
to 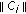
If
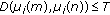
-
(4.3.1.1)
 ;
; -
(4.3.1.2)
 (Note "\" is the operation of Set Difference)
(Note "\" is the operation of Set Difference) -
(4.3.1.3)
Go to step 4.3;
Else
-
Go to step (4.3.1)
-
(4.3.1.1)
-
(4.3.1)
-
(4.4)
If
 (At the final iteration,
(At the final iteration,  is either 0 or 1 depending on Step
is either 0 or 1 depending on Step  )
)clustering_completed:= TRUE;
Else
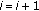 ;
;
-
(4.1)
-
(5)
Final cluster configuration
 ;
;
The most accurate way of pairing up colours/clusters is to conduct an exhaustive search and pair up the closest ones. However, we observed that the size of the colour table of  -pixel images normally varies from 100,000 to 700,000. Exhaustive search in such an enormous colour table is by no means computationally feasible. So we employ a suboptimal, yet more efficient search method, called incremental clustering based on the idea proposed by Jain et al. [17]. The idea is that patterns are sorted in a random order, each treated as singleton clusters, and then incrementally merged to form larger clusters. When growing a cluster, the algorithm searches for the first pattern or cluster outside the growing cluster, with a distance to the growing cluster's centroid shorter than a threshold, to merge. According to [17], the time complexity of a
-pixel images normally varies from 100,000 to 700,000. Exhaustive search in such an enormous colour table is by no means computationally feasible. So we employ a suboptimal, yet more efficient search method, called incremental clustering based on the idea proposed by Jain et al. [17]. The idea is that patterns are sorted in a random order, each treated as singleton clusters, and then incrementally merged to form larger clusters. When growing a cluster, the algorithm searches for the first pattern or cluster outside the growing cluster, with a distance to the growing cluster's centroid shorter than a threshold, to merge. According to [17], the time complexity of a  -means clustering algorithm is
-means clustering algorithm is  , where
, where  is the number of the colours to be clustered,
is the number of the colours to be clustered,  is the number of the clusters in the final cluster configuration, and
is the number of the clusters in the final cluster configuration, and  is the number of iterations taken by the algorithm before convergence. In comparison, the time complexity of the incremental clustering algorithm is only
is the number of iterations taken by the algorithm before convergence. In comparison, the time complexity of the incremental clustering algorithm is only  .
.
Let  be the colour table,
be the colour table,  the set of clusters in the
the set of clusters in the  th iteration of the clustering process,
th iteration of the clustering process,  the
the  cluster in
cluster in  the centroids of
the centroids of  the Euclidean distance between the centroids
the Euclidean distance between the centroids  and
and  of clusters
of clusters  and
and  a Euclidean distance threshold, and
a Euclidean distance threshold, and  the final clustering configuration of the colour table
the final clustering configuration of the colour table  . The proposed PEC algorithm is described in Algorithm 1.
. The proposed PEC algorithm is described in Algorithm 1.
Figure 2 illustrates an example of the working of the PEC algorithm. Each circle represents a colour in the colour table  to be clustered. At the beginning of Iteration 0 in Figure 2
to be clustered. At the beginning of Iteration 0 in Figure 2 , every individual colour is considered as a singleton cluster, and all of the circles/colours are sorted, with their indices determined by a secret key
, every individual colour is considered as a singleton cluster, and all of the circles/colours are sorted, with their indices determined by a secret key  . At the end of Iteration 0 as demonstrated in Figure 2
. At the end of Iteration 0 as demonstrated in Figure 2 , each circle/colour is either paired up with another with a distance shorter than
, each circle/colour is either paired up with another with a distance shorter than  to form a new cluster
to form a new cluster  of
of  or left in
or left in  . At the beginning of Iteration 1, as demonstrated in Figure 2
. At the beginning of Iteration 1, as demonstrated in Figure 2 , the centroids (represented as dots) of the successfully paired clusters in
, the centroids (represented as dots) of the successfully paired clusters in  are calculated. Based on the centroids of the successfully paired groups, the clustering continues in Iteration 1 (see Figure 2(d)). After Iteration 1, there is only one cluster left, which satisfies
are calculated. Based on the centroids of the successfully paired groups, the clustering continues in Iteration 1 (see Figure 2(d)). After Iteration 1, there is only one cluster left, which satisfies  in step (4.4) of Algorithm 1. Therefore, the PEC algorithm stops.
in step (4.4) of Algorithm 1. Therefore, the PEC algorithm stops.
In order to demonstrate the idea of the PEC algorithm in a simple manner, let us use a scalar number to represent a colour of  in the following example. For example, given
in the following example. For example, given  after randomisation under the control of a secret key
after randomisation under the control of a secret key  , and the threshold
, and the threshold  , the clustering process is as follows.
, the clustering process is as follows.
After Iteration 0,

After Iteration 1,

Since  , according to step (4.4) and (5) of Algorithm 1, the final clustering is
, according to step (4.4) and (5) of Algorithm 1, the final clustering is

 is a clustering configuration consisting of clusters of various sizes, and the size of a cluster
is a clustering configuration consisting of clusters of various sizes, and the size of a cluster  is
is  . Therefore, the embedding capacity for a pixel, whose colour belongs to
. Therefore, the embedding capacity for a pixel, whose colour belongs to  , is
, is  bits. Meanwhile, every colour in cluster
bits. Meanwhile, every colour in cluster  may be used for substitution during the secret data hiding process, hence there is no redundancy in
may be used for substitution during the secret data hiding process, hence there is no redundancy in  . In addition, although
. In addition, although  contains only one colour and is not embeddable, such a cluster can be expanded to a larger cluster by the expansion algorithm as introduced in Section 2.3, and thus
contains only one colour and is not embeddable, such a cluster can be expanded to a larger cluster by the expansion algorithm as introduced in Section 2.3, and thus  is included in
is included in  .
.
In step (4.3) of Algorithm 1, for one pixel to be paired, the algorithm selects the first colour in the colour table smaller than the distance threshold  rather than the closest colour. This selection policy has two advantages. Firstly, it avoids exhaustive search and greatly reduces the computation load [17]. Secondly, this selection policy increases the security of the PEC-based steganographic scheme because it is sensitive to the orders of the colours in the colour table. For example, in Iteration 0 of the above demonstration, 17 is closer to 15. However, 15 is paired up with 11 since 11 appears before 17 in the colour table, and the distance between 11 and 15 is
rather than the closest colour. This selection policy has two advantages. Firstly, it avoids exhaustive search and greatly reduces the computation load [17]. Secondly, this selection policy increases the security of the PEC-based steganographic scheme because it is sensitive to the orders of the colours in the colour table. For example, in Iteration 0 of the above demonstration, 17 is closer to 15. However, 15 is paired up with 11 since 11 appears before 17 in the colour table, and the distance between 11 and 15 is  . By randomising the orders of the colours of the colour table in Step 1 of the PEC algorithm according to secret key
. By randomising the orders of the colours of the colour table in Step 1 of the PEC algorithm according to secret key  , we can ensure the security of the proposed scheme. Without this secret key, even if a potential attacker managed to establish the same colour table, he/she is still unable to obtain the same clustering configuration
, we can ensure the security of the proposed scheme. Without this secret key, even if a potential attacker managed to establish the same colour table, he/she is still unable to obtain the same clustering configuration  . Without the same clustering configuration
. Without the same clustering configuration  , the attacker is unable to extract the correct secret data.
, the attacker is unable to extract the correct secret data.
2.3. Cluster Expansion
If the colour of a pixel belongs to a cluster with  colours, then this pixel can carry
colours, then this pixel can carry  bits of secret message. Therefore, by expanding clusters exponentially, higher embedding capacity can be achieved. For example, a cluster with 4 (
bits of secret message. Therefore, by expanding clusters exponentially, higher embedding capacity can be achieved. For example, a cluster with 4 ( ) colours has the embedding capacity of 2 bits. If 4 more different colours are inserted into this cluster, the embedding capacity of the colours in this cluster increases to 3 bits (
) colours has the embedding capacity of 2 bits. If 4 more different colours are inserted into this cluster, the embedding capacity of the colours in this cluster increases to 3 bits ( ). However, despite the increased capacity, the cluster expansion may also lead to higher embedding distortion if not done in an adaptive manner with regard to the details of the content in the image. Therefore the following two factors need to be taken into account when expanding clusters.
). However, despite the increased capacity, the cluster expansion may also lead to higher embedding distortion if not done in an adaptive manner with regard to the details of the content in the image. Therefore the following two factors need to be taken into account when expanding clusters.
-
(i)
We observed that, for most images without larger homogeneous areas, higher embedding capacity can be achieved without incurring further distortion in terms of both human perception and PSNRs if the added virtual colours are within one standard deviation of the cluster centroid. However, if there are larger homogeneous areas in the image, although the PSNR remains near constant, visual distortion may become more noticeable when too many virtual colours are added to the homogeneous areas. Therefore, the number of the virtual colours should be restricted in the expansion process.
-
(ii)
Another factor worth noting is that overexpansion cannot guarantee the presence of every virtual colour in the stego-image. As a result, the recipient of the stego-image cannot obtain the same colour table as used at the embedding side; consequently he/she is unable to make the correct extraction. Therefore, measures for tackling this situation are necessary.
Let  be the expanded counterpart of
be the expanded counterpart of  the size of
the size of  (i.e.,
(i.e.,  ), and
), and  the number of pixels whose colours belong to cluster
the number of pixels whose colours belong to cluster  . One necessary (but not sufficient) condition for all the colours in cluster
. One necessary (but not sufficient) condition for all the colours in cluster  to appear in the stego-image is
to appear in the stego-image is  . Without loss of generality, we assume that the secret data is uniformly distributed, that is, the probability of the occurrence of every
. Without loss of generality, we assume that the secret data is uniformly distributed, that is, the probability of the occurrence of every  -bit secret data segment in the entire secret data stream is
-bit secret data segment in the entire secret data stream is  . For example, in a uniformly distributed secret data sequence, the probability of the occurrence of every 2-bit secret data segment ("00", "01", "11" and "10") is
. For example, in a uniformly distributed secret data sequence, the probability of the occurrence of every 2-bit secret data segment ("00", "01", "11" and "10") is  . According to the data hiding algorithm (described in Section 2.4), the colour, with its index equal to the secret data bits will be substituted in order to carry the secret data bits, will be substituted in order to carry the secret data bits. Therefore, the probability for one colour to be substituted is
. According to the data hiding algorithm (described in Section 2.4), the colour, with its index equal to the secret data bits will be substituted in order to carry the secret data bits, will be substituted in order to carry the secret data bits. Therefore, the probability for one colour to be substituted is  . Consequently, the probability of one colour not being substituted is
. Consequently, the probability of one colour not being substituted is  . Performing data embedding on
. Performing data embedding on  pixels whose colours are in the same cluster of size
pixels whose colours are in the same cluster of size  , the possibility
, the possibility  of one colour in this cluster not being substituted is
of one colour in this cluster not being substituted is

Therefore, the expansion should not result in a value of  greater than a given upper bound
greater than a given upper bound  (i.e.,
(i.e.,  ). That is to say that the following inequality must be satisfied:
). That is to say that the following inequality must be satisfied:

Additionally, the radius of the expanded cluster should also be smaller than the Euclidian distance threshold 

where the right-hand side of Inequality (6) is the volume of a 3-deminsional sphere with a radius equal to  . We also require that the size of the expanded cluster still equals a power of 2, in order to avoid redundancy. Therefore, taking the aforementioned factors into consideration, the size of the expanded cluster,
. We also require that the size of the expanded cluster still equals a power of 2, in order to avoid redundancy. Therefore, taking the aforementioned factors into consideration, the size of the expanded cluster,  , should satisfy
, should satisfy

where  is the floor function. The cluster expansion algorithm is presented in Algorithm 2. After applying the cluster expansion to all clusters in the original colour table
is the floor function. The cluster expansion algorithm is presented in Algorithm 2. After applying the cluster expansion to all clusters in the original colour table  , the result is an expanded colour table
, the result is an expanded colour table  .
.
Algorithm 2: Cluster expansion algorithm.
Input: cluster  , probability upper bound
, probability upper bound  and Euclidean distance threshold
and Euclidean distance threshold 
Output: expanded cluster 
Cluster expansion algorithm
-
(1)
Compute
 (the number of pixels with their colours belonging to
(the number of pixels with their colours belonging to  );
); -
(2)
Compute the centroid
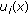 of cluster
of cluster 
-
(3)
Compute
 of Inequality (5);
of Inequality (5); -
(4)
Compute
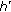 according to (7);
according to (7); -
(5)
Let
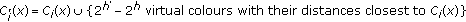 . Note
. Note
that by "virtual colours" we mean the colours that are not present in  and
and
 .
.
To ensure the appearance of every virtual colour in the stego-image and subsequently allow the recipient to reconstruct the same colour table  , some pixels have to be chosen to have their original (physical) colours replaced with the virtual colours before data hiding takes place (step (4) of Figure 1). To assign a virtual colour, we identify the first pixel in the image with a physical colour in the same cluster as the virtual colour. Assigning each virtual colour to only one pixel keeps the distortion low. Note that this "expansion" distortion is insignificant when compared to the actual embedding distortion, as discussed in Section 3 and demonstrated in Table 4 and Figures 7 and 8.
, some pixels have to be chosen to have their original (physical) colours replaced with the virtual colours before data hiding takes place (step (4) of Figure 1). To assign a virtual colour, we identify the first pixel in the image with a physical colour in the same cluster as the virtual colour. Assigning each virtual colour to only one pixel keeps the distortion low. Note that this "expansion" distortion is insignificant when compared to the actual embedding distortion, as discussed in Section 3 and demonstrated in Table 4 and Figures 7 and 8.
Because the virtual colours are not added after the preliminary PEC clustering, there is no guarantee that the cluster configuration can be reconstructed. Therefore after cluster expansion and performing step (4) of Figure 1, a second round of PEC clustering (step (5) of Figure 1) is applied to partition the expanded colour table  so as to create a new cluster configuration
so as to create a new cluster configuration  before data hiding.
before data hiding.
2.4. Data Hiding and Extraction
The data hiding process is straightforward and is presented in Algorithm 3. At the receiving side, the recipient has to construct the same colour table  according to the received image
according to the received image  , and then apply the same PEC algorithm on
, and then apply the same PEC algorithm on  in order to obtain the same clustering configuration
in order to obtain the same clustering configuration  . With the same
. With the same  and
and  the secret data can be extracted correctly. The extraction algorithm performs as follows. If the colour of a pixel is the only member of its cluster
the secret data can be extracted correctly. The extraction algorithm performs as follows. If the colour of a pixel is the only member of its cluster  , then this pixel carries no information; otherwise, the index of the colour in the cluster represents the secret data bits. After visiting all pixels, by concatenating those extracted bits, the complete secret data stream can be revealed. The data extraction algorithm is presented in Algorithm 4.
, then this pixel carries no information; otherwise, the index of the colour in the cluster represents the secret data bits. After visiting all pixels, by concatenating those extracted bits, the complete secret data stream can be revealed. The data extraction algorithm is presented in Algorithm 4.
Algorithm 3: Data hiding algorithm.
Input: modified image  , cluster configuration
, cluster configuration  , secret key
, secret key  , secret data
, secret data 
Output: embedded image 
Embedding algorithm
-
(1)
Convert
 into binary form;
into binary form; -
(2)
While the end of the input image
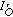 is not raeached
is not raeachedIf the colour of the current pixel
 is the only member of its cluster
is the only member of its cluster  (i.e., this pixel is non-embeddable)
(i.e., this pixel is non-embeddable)-
(2.1)
Go to Step 2;
Else
-
(2.2)
Take
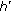 (
( )?bits from
)?bits from  , denoted as
, denoted as 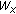 ;
; -
(2.3)
Replace the current colour with the
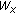 th colour in
th colour in  ;
;
-
(2.1)
Algorithm 4: Data extraction algorithm.
Input: received image  , secret key
, secret key  , threshold
, threshold 
Output: extracted secret data 
Extraction algorithm
-
(1)
Create the colour table
 based on
based on 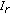 ; (Note no cluster expansion is needed.)
; (Note no cluster expansion is needed.) -
(2)
Apply the PEC algorithm on
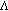 to get the cluster configuration
to get the cluster configuration 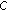 using the same threshold
using the same threshold 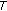 and the shared secret key
and the shared secret key 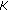 ;
; -
(3)
While the end of
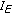 is not reached
is not reachedIf the colour of the current pixel
 is the only member of its cluster
is the only member of its cluster 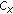 (i.e.,
(i.e.,  is non-embeddable)
is non-embeddable)-
(3.1)
go to step
 ;
;Else
-
(3.2)
Convert the index
 of the colour in
of the colour in 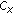 into binary form;
into binary form; -
(3.3)
Append
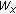 to the binary stream of the secret data
to the binary stream of the secret data 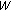 extracted so far;
extracted so far;
-
(3.1)
3. Experimental Results
In Figures 3 to 6, we show 4 original images and their corresponding stego-images with different values of Euclidean distance threshold  . In these figures, we can see that when
. In these figures, we can see that when  , the distortion is imperceptible by human eyes. However, as
, the distortion is imperceptible by human eyes. However, as  increases further, the distortion becomes more noticeable. The following experiments conform to this result (see Table 4). Although the greater the
increases further, the distortion becomes more noticeable. The following experiments conform to this result (see Table 4). Although the greater the  is, the higher the embedding capacity becomes because there is bigger room for cluster expansion, the distortion also increases. On the other hand, the smaller
is, the higher the embedding capacity becomes because there is bigger room for cluster expansion, the distortion also increases. On the other hand, the smaller  is, the lower the distortion becomes. However, the embedding capacity decreases because the room for cluster expansion becomes more limited. Therefore, in our experiments, we set
is, the lower the distortion becomes. However, the embedding capacity decreases because the room for cluster expansion becomes more limited. Therefore, in our experiments, we set  to 3 and 4. We also set the upper bound
to 3 and 4. We also set the upper bound  of Inequality (5) to 0.001.
of Inequality (5) to 0.001.
The size of the host image is an important factor of the embedding capacity because a large image normally contains more colours than a smaller one, which results in larger clusters with higher embedding capacity. Meanwhile, since the homogeneous background areas in an image only contain a limited number of colours, images with large homogeneous areas tend to have a smaller colour table, but greater rooms for cluster expansion. We use two  -pixel images as examples, one with a large homogenous area (as shown in Figure 7(a)), thus a smaller colour table, while the other without a homogeneous background (as shown in Figure 8(a)), thus a larger colour table. Whether an image has a large homogeneous area can be determined by the size of the colour table. A large colour table means that every colour only appears a few times, indicating that there is no large homogenous area in the image, and vice verse. Given the images of the same size, the ratio between the total number of pixel and the size of the colour table can give a good indication as to whether there are large homogeneous areas in the images or not. For example, for the "Hill" image, the ratio between the total number of pixel, and the size of the colour table is 7.1 : 1 while the ratio for "Mandrill" is 1.6 : 1. Each colour has appeared about 7 times on average in the "Hill" image, while each colour only has appeared 1.6 times on average in the "Mandrill" image. Therefore we can conclude that there are larger homogeneous areas in "Hill" than those in "Mandrill." Table 1 lists the statistics of the cluster expansion with the distance threshold
-pixel images as examples, one with a large homogenous area (as shown in Figure 7(a)), thus a smaller colour table, while the other without a homogeneous background (as shown in Figure 8(a)), thus a larger colour table. Whether an image has a large homogeneous area can be determined by the size of the colour table. A large colour table means that every colour only appears a few times, indicating that there is no large homogenous area in the image, and vice verse. Given the images of the same size, the ratio between the total number of pixel and the size of the colour table can give a good indication as to whether there are large homogeneous areas in the images or not. For example, for the "Hill" image, the ratio between the total number of pixel, and the size of the colour table is 7.1 : 1 while the ratio for "Mandrill" is 1.6 : 1. Each colour has appeared about 7 times on average in the "Hill" image, while each colour only has appeared 1.6 times on average in the "Mandrill" image. Therefore we can conclude that there are larger homogeneous areas in "Hill" than those in "Mandrill." Table 1 lists the statistics of the cluster expansion with the distance threshold  equal to 3 and 4. We only choose the distance threshold 3 and 4 for experiments because when the threshold is higher than 4, the distortion is too high (PSNR is lower than 35 db) and when the threshold is lower than 3, the room for expansion is too small (the threshold equal to 2 hardly allows any expansion in the cluster expansion phase). We can see that image "Hill" in Figure 7(a), with a relatively larger homogeneous background than image "Mandrill" in Figure 8(a), has a more significant expansion rate. Because one virtual colour is assigned to only one pixel in the image, the distortion arising from the expansion operation is well above 60 dB (see "Distortion due to expansion" of Table 1). Figures 7(b) and 8(b) are the slightly modified version of Figures 7(a) and 8(a) with virtual colours added when distance threshold
equal to 3 and 4. We only choose the distance threshold 3 and 4 for experiments because when the threshold is higher than 4, the distortion is too high (PSNR is lower than 35 db) and when the threshold is lower than 3, the room for expansion is too small (the threshold equal to 2 hardly allows any expansion in the cluster expansion phase). We can see that image "Hill" in Figure 7(a), with a relatively larger homogeneous background than image "Mandrill" in Figure 8(a), has a more significant expansion rate. Because one virtual colour is assigned to only one pixel in the image, the distortion arising from the expansion operation is well above 60 dB (see "Distortion due to expansion" of Table 1). Figures 7(b) and 8(b) are the slightly modified version of Figures 7(a) and 8(a) with virtual colours added when distance threshold  , respectively. Table 2 demonstrates the changes to the size of the largest cluster of image "Hill" and "Mandrill" after cluster expansion. For image "Hill," the size of the largest cluster doubles (from 64 up to 128) after the expansion when the threshold is either 3 or 4. So those pixels with their colour belonging to this cluster can carry 7 (
, respectively. Table 2 demonstrates the changes to the size of the largest cluster of image "Hill" and "Mandrill" after cluster expansion. For image "Hill," the size of the largest cluster doubles (from 64 up to 128) after the expansion when the threshold is either 3 or 4. So those pixels with their colour belonging to this cluster can carry 7 ( ) bits of secret data, rather than just 6 (
) bits of secret data, rather than just 6 ( ) bits. Note that there are other clusters of various sizes underwent expansion. For the image of "Mandrill" with a lower expansion rate as shown in Table 2, the largest cluster has not been expanded due to the constraints (mentioned in Section 2.3) imposed on the expansion algorithm.
) bits. Note that there are other clusters of various sizes underwent expansion. For the image of "Mandrill" with a lower expansion rate as shown in Table 2, the largest cluster has not been expanded due to the constraints (mentioned in Section 2.3) imposed on the expansion algorithm.
 . Note that "Distortion due to expansion" is the distortion incurred after one virtual colour is assigned to one pixel in the original image.
. Note that "Distortion due to expansion" is the distortion incurred after one virtual colour is assigned to one pixel in the original image.Tables 3 and 4 show that the proposed scheme is capable of improving the embedding capacity in terms of bit per pixel (bpp) without inflicting distortion on the stego-images. For image "Hill," we can see the significant capacity difference between the unexpanded and the expanded cases as shown in Table 3 while embedding distortion remains near constant as shown in Table 4. Note that Table 4 even shows slight reduction in distortion (i.e., the increase of PSNR from 38.22 dB to 38.82 dB) after cluster expansion on "Hill" with  . Although the general perception is that high embedding capacity is usually gained at the expenses of high distortion, such a distortion reduction is still possible due to the fact that the virtual colours are only added around the centroids of the clusters under the constraints mentioned in Section 2.3. The least upper bound of embedding distortion is the mean Euclidean distance of each group (determined by the triangle inequality). Adding virtual colours around the centroid of the clusters can reduce the mean Euclidean distance of each group and therefore reduce embedding distortion. However, in Table 3, in the image of "Mandrill" wherein the high-frequency signal prevails, rooms for cluster expansion are relatively limited (see Table 1, expansion rate), and performance improvement gained through cluster expansion is therefore insignificant. Figures 7(c) and 8(c) are the stego-images of Figures 7(a) and 8(a) with virtual colours added when distance threshold
. Although the general perception is that high embedding capacity is usually gained at the expenses of high distortion, such a distortion reduction is still possible due to the fact that the virtual colours are only added around the centroids of the clusters under the constraints mentioned in Section 2.3. The least upper bound of embedding distortion is the mean Euclidean distance of each group (determined by the triangle inequality). Adding virtual colours around the centroid of the clusters can reduce the mean Euclidean distance of each group and therefore reduce embedding distortion. However, in Table 3, in the image of "Mandrill" wherein the high-frequency signal prevails, rooms for cluster expansion are relatively limited (see Table 1, expansion rate), and performance improvement gained through cluster expansion is therefore insignificant. Figures 7(c) and 8(c) are the stego-images of Figures 7(a) and 8(a) with virtual colours added when distance threshold  , respectively.
, respectively.
As discussed above, adding the virtual colours to expand the cluster size can boost the performance of PEC. A more critical way of demonstrating the PEC algorithm's superiority to  -means algorithm is to perform PEC without adding virtual colours (i.e., a handicapped version of PEC). We compared the CW method reported in [1] and PEC by applying them to Lena image of
-means algorithm is to perform PEC without adding virtual colours (i.e., a handicapped version of PEC). We compared the CW method reported in [1] and PEC by applying them to Lena image of  -pixels and 256 gray levels as shown in Figure 9. CW is a VQ-based method; to conduct comparisons on the same basis, we generate a codebook containing 512 codewords, each represented as
-pixels and 256 gray levels as shown in Figure 9. CW is a VQ-based method; to conduct comparisons on the same basis, we generate a codebook containing 512 codewords, each represented as  -pixel image block. The reader is referred to [4] for details about how the codebook is generated. Compared to the previous case with colour images as target images, the colour table is now replaced with the codebook of 512 codewords, and each image is divided into blocks of
-pixel image block. The reader is referred to [4] for details about how the codebook is generated. Compared to the previous case with colour images as target images, the colour table is now replaced with the codebook of 512 codewords, and each image is divided into blocks of  -pixels and replaced with the most similar codeword. Algorithm one is then used to cluster the codebook, but we do not apply Algorithm 2 to expand the clustered codebook. Algorithms 2 and 3 are applied to embedding and extracting secret data. Since the embedding capacity and embedding distortion cannot be evaluated alone without taking each other into account, a reasonable way of evaluating them would be to fix one of the two factors and see how the algorithm performs in terms of the other factor. Figures 10(a) and 10(b) are the results of experiments with the threshold
-pixels and replaced with the most similar codeword. Algorithm one is then used to cluster the codebook, but we do not apply Algorithm 2 to expand the clustered codebook. Algorithms 2 and 3 are applied to embedding and extracting secret data. Since the embedding capacity and embedding distortion cannot be evaluated alone without taking each other into account, a reasonable way of evaluating them would be to fix one of the two factors and see how the algorithm performs in terms of the other factor. Figures 10(a) and 10(b) are the results of experiments with the threshold  , which is the Euclidean distance between vectors, equal to 20 and 60, respectively. We can see that at any embedding capacity, the embedding distortion of the proposed PEC algorithm is always lower (higher PSNRs). For example, in Figure 10(b), when the embedding capacity (the horizontal axis) is 8000 bits, the distortions inflicted on the image by the CW and the proposed PEC algorithms are 29.81 dB and 31.82 dB, respectively. We can also see from Figure 10 that at certain value of embedding distortion along the vertical axis, the embedding capacity of the PEC algorithm is always greater than that of the CW algorithm. The reader is reminded that the CW algorithm is greedier in merging codewords. Therefore, with the same threshold, the CW algorithm should have a higher maximal capacity. That is why the two cutoff points where the maximal embedding capacities are reached are different. But this does not mean that the CW algorithm has better performance in terms of embedding capacity because the performance should be measured in terms of both embedding capacity and distortion. As we will discuss below, the PEC algorithm can still reach the same embedding capacity with a higher threshold
, which is the Euclidean distance between vectors, equal to 20 and 60, respectively. We can see that at any embedding capacity, the embedding distortion of the proposed PEC algorithm is always lower (higher PSNRs). For example, in Figure 10(b), when the embedding capacity (the horizontal axis) is 8000 bits, the distortions inflicted on the image by the CW and the proposed PEC algorithms are 29.81 dB and 31.82 dB, respectively. We can also see from Figure 10 that at certain value of embedding distortion along the vertical axis, the embedding capacity of the PEC algorithm is always greater than that of the CW algorithm. The reader is reminded that the CW algorithm is greedier in merging codewords. Therefore, with the same threshold, the CW algorithm should have a higher maximal capacity. That is why the two cutoff points where the maximal embedding capacities are reached are different. But this does not mean that the CW algorithm has better performance in terms of embedding capacity because the performance should be measured in terms of both embedding capacity and distortion. As we will discuss below, the PEC algorithm can still reach the same embedding capacity with a higher threshold  while keeping the embedding distortion lower than that of the CW algorithm using a lower threshold
while keeping the embedding distortion lower than that of the CW algorithm using a lower threshold  .
.
Distortion comparison between the PEC and CW algorithm when applied to Figure 9 with the threshold  equal to (a) 20 and (b) 60.
equal to (a) 20 and (b) 60.
Another way to look at the performance is to compare the maximal embedding capacity across a wide range of threshold values under the constraint that the embedding distortion should not go below a specific lower bound. Figures 11(a) and 11(b) show the curves of embedding capacity under the constraints that the embedding distortion should not go below the lower bound of 35 db and 30 db, respectively. At the beginning, the PSNR is lower than the lower bound due to the low capacity and hence the curves keep rising as the threshold increases, until the peaks of the curves are reached. The capacity starts to drop after the peaks are reached because as the threshold  increases, the sizes of the clusters become greater. As a result, embedding the same amount of data incurs higher distortion. That means that the lower bound of distortion will be reached when less data is embedded with greater
increases, the sizes of the clusters become greater. As a result, embedding the same amount of data incurs higher distortion. That means that the lower bound of distortion will be reached when less data is embedded with greater  . In Figure 11(a), the maximal capacity of the PEC algorithm is 7457 bits (appearing at threshold
. In Figure 11(a), the maximal capacity of the PEC algorithm is 7457 bits (appearing at threshold  ), while that of the CW algorithm equals 6810 bits (appearing at threshold
), while that of the CW algorithm equals 6810 bits (appearing at threshold  ). In Figure 11(b), the maximal capacity of the PEC algorithm is 11070 bits (appearing at threshold
). In Figure 11(b), the maximal capacity of the PEC algorithm is 11070 bits (appearing at threshold  ), while that of the CW algorithm equals 8979 bits (appearing at threshold
), while that of the CW algorithm equals 8979 bits (appearing at threshold  ). We can see that in both cases the performance of the PEC algorithm in terms of maximal embedding capacity is 9.5% and 23.3%, respectively, superior to that of the CW algorithm.
). We can see that in both cases the performance of the PEC algorithm in terms of maximal embedding capacity is 9.5% and 23.3%, respectively, superior to that of the CW algorithm.
Embedding capacity comparison between the PEC and CW algorithm when applied to Figure 9 with the threshold PSNR set to (a) 35 dB and (b) 30 dB.
4. Analyses of PEC
4.1. Histogram Analysis and  -Secure
-Secure
The histogram of an image can effectively reveal the distribution of the colours or intensities, and thus any irregular distribution caused by the steganographic method can be easily detected [18]. In [15, 16], the 3-dimensional RGB colour space is separated into spheres by the  -means clustering algorithm, and colours generated around the centre of the sphere are used for substitution in order to carry secret messages while the colours outside the sphere are not used in the stego-images. Moreover, within each sphere, the colours distribute sparsely and uniformly. As a result, a large number of gaps would appear between colours with high occurrences in the histograms of the stego-images. Such a phenomenon usually do not appear in natural images, therefore its appearance would attract the steganalyst's attention. This is why histogram and histogram characteristic functions have been extensively used in measuring the security of stegonagraphic schemes [18–20]. By analysing the histogram of the stego-image, the attacker can easily detect the spheres in the form of aggregated clusters separated by large gaps in the histogram. These gaps allow the attacker to reconstruct the sphere/cluster configuration and even infer the hidden message. Compared to [15, 16], the proposed PEC algorithm does not separate the 3-deminsional RGB colour for generating colours. Instead, all the physical colours are preserved while some virtual colours are added to expand the clusters in order to increase embedding capacity without inflicting high distortion. Hence, the attacker cannot detect separated clusters in the histogram.
-means clustering algorithm, and colours generated around the centre of the sphere are used for substitution in order to carry secret messages while the colours outside the sphere are not used in the stego-images. Moreover, within each sphere, the colours distribute sparsely and uniformly. As a result, a large number of gaps would appear between colours with high occurrences in the histograms of the stego-images. Such a phenomenon usually do not appear in natural images, therefore its appearance would attract the steganalyst's attention. This is why histogram and histogram characteristic functions have been extensively used in measuring the security of stegonagraphic schemes [18–20]. By analysing the histogram of the stego-image, the attacker can easily detect the spheres in the form of aggregated clusters separated by large gaps in the histogram. These gaps allow the attacker to reconstruct the sphere/cluster configuration and even infer the hidden message. Compared to [15, 16], the proposed PEC algorithm does not separate the 3-deminsional RGB colour for generating colours. Instead, all the physical colours are preserved while some virtual colours are added to expand the clusters in order to increase embedding capacity without inflicting high distortion. Hence, the attacker cannot detect separated clusters in the histogram.
Katzenbeisser and Petitcolas [21] propose the statistical concept of  -secure as a more strict security requirement based on the histogram analysis.
-secure as a more strict security requirement based on the histogram analysis.  -secure requires that, for steganography scheme to be deemed as secure, the Kullback-Leibler divergence (
-secure requires that, for steganography scheme to be deemed as secure, the Kullback-Leibler divergence ( ) between the PDF (probability distribution function) of the original signal and the stego-signal must be less than a given threshold
) between the PDF (probability distribution function) of the original signal and the stego-signal must be less than a given threshold  . The Kullback-Leibler divergence (
. The Kullback-Leibler divergence ( ) can be described as follows:
) can be described as follows:

where  and
and  are the PDF of the original image and the stego-images. In the proposed PEC algorithm, the
are the PDF of the original image and the stego-images. In the proposed PEC algorithm, the  between the images are about 0.001 to 0.02 (except the embedding result of the Airplane image, which is a particular example that the image contains over 80% homogenous area, allowing the PEC algorithm to expand the clusters with a greater expansion rate) depending on the content of the images. Table 5 demonstrates the KL divergence of the images. We can see that
between the images are about 0.001 to 0.02 (except the embedding result of the Airplane image, which is a particular example that the image contains over 80% homogenous area, allowing the PEC algorithm to expand the clusters with a greater expansion rate) depending on the content of the images. Table 5 demonstrates the KL divergence of the images. We can see that  is always lower than 0.01 when
is always lower than 0.01 when  .
.
 ) of the images
) of the images4.2. Characteristics of the PEC
There are three main advantageous aspects to the idea of the proposed PEC-based steganographic scheme.
-
(i)
The pairwise matching operation ensures that the sizes of all clusters are always equal to a power of 2 (i.e., exponential). This exponential structure makes use of every colour in a cluster for hiding data and thus removes redundancy in the data hiding process.
-
(ii)
The cluster expansion algorithm allows the embedding capacity to be increased without sacrificing imperceptibility. At first glance, distortion should increase proportionally as the embedding capacity gets higher through the addition of the virtual colours. However the cluster expansion algorithm can actually decrease the embedding distortion in terms of PSNR by shortening the average distance between the colours and the centroid of the cluster. According to the cluster expansion algorithm, clusters are expanded not by extending their boundaries outwards, but by increasing the population density around the centroids while leaving the boundary intact, thus reducing colour variation of each cluster.
-
(iii)
The PEC-based steganography strengthens security. Ensuring the presences of all physical and virtual colours in the stego-image, the recipient can re-establish the same cluster configuration using the shared secret key
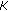 and distance threshold
and distance threshold  . Sharing the large colour palette and the centroids of the clusters (as required in [15, 16]) is no longer necessary. The reason the security of the PEC-based steganographic scheme is strengthened is twofold.
. Sharing the large colour palette and the centroids of the clusters (as required in [15, 16]) is no longer necessary. The reason the security of the PEC-based steganographic scheme is strengthened is twofold.-
(a)
Because there is no need to transmit extrainformation, the chance of compromising the security of the scheme is reduced.
-
(b)
Because of the fragility of the PEC-based steganographic scheme, modifications on the stego-image will inevitably change the colours of the pixels and thus lead to a different colour table. It is noted that the PEC algorithm is very sensitive to the initial colour table. With a different colour table, the PEC algorithm will produce a greatly different clustering configuration and wrong ordering of the colours within each cluster, which will prevent the hidden data being extracted by the attacker.
-
(a)
5. Conclusions
After studying some clustering-based steganographic schemes for colour images, we observed that the performance of a scheme depends on the efficiency of the clustering algorithm. An efficient clustering algorithm should take the two conflicting factors of high embedding capacity and low embedding distortion into account simultaneously. In this paper, we have proposed a novel steganographic scheme using the Progressive Exponential Clustering (PEC) algorithm. This algorithm overcomes the limitation of the traditional clustering-based steganographic schemes by seeking a balance between high embedding capacity and low embedding distortion. Meanwhile, this steganographic scheme employs a cluster expansion method, which further increases the capacity without sacrificing imperceptibility. Our experiments have proved that adding virtual colours in an adaptive manner to the colour table of images with significant low-frequency components can significantly increase the embedding capacity without inflicting distortion on the stego-images.
References
Chang C-C, Wu W-C: Hiding secret data adaptively in vector quantisation index tables. IEE Proceedings: Vision, Image and Signal Processing 2006, 153(5):589-597. 10.1049/ip-vis:20050153
Du W-C, Hsu W-J: Adaptive data hiding based on VQ compressed images. IEE Proceedings: Vision, Image and Signal Processing 2003, 150(4):233-238. 10.1049/ip-vis:20030525
Fridrich J, Du R: Secure steganographic methods for palette images. Proceedings of the 3rd Information Hiding Workshop, 2000, Lecture Notes in Computer Science 1768: 47-60.
Li Y, Li C-T: Steganographic scheme for VQ compressed images using progressive exponential clustering. Proceedings of the IEEE International Conference on Video and Signal Based Surveillance (AVSS '06), 2006, Sydney, Australia
Lin C-C, Chen S-C, Hsueh N-L: Adaptive embedding techniques for VQ-compressed images. Information Sciences 2009, 179(1-2):140-149. 10.1016/j.ins.2008.09.001
Niimi M, Noda H, Kawaguchi E, Eason RO: High capacity and secure digital steganography to palette-based images. Proceedings of the International Conference on Image Processing (ICIP '02), September 2002, Rochester, NY, USA 917-920.
Niimi M, Noda H, Kawaguchi E, Eason RO: Luminance quasi-preserving color quantization for digital steganography to palette-based images. Proceedings of the International Conference on Pattern Recognition, August 2002 251-254.
Raja KB, Siddaraju S, Venugopal KR, Patnaik LM: Secure steganography using colour palette decomposition. Proceedings of the International Conference on Signal Processing, Communications and Networking (ICSCN '07), February 2007 74-80.
Tai W-L, Chang C-C: Data hiding based on VQ compressed images using hamming codes and declustering. International Journal of Innovative Computing, Information and Control 2009, 5(7):2043-2052.
Wang X, Yao Z, Li C-T: A palette-based image steganographic method using colour quantisation. Proceedings of the International Conference on Image Processing (ICIP '05), September 2005, Genova, Italy 2: 1090-1093.
Wu M-Y, Ho Y-K, Lee J-H: An iterative method of palette-based image steganography. Pattern Recognition Letters 2004, 25(3):301-309. 10.1016/j.patrec.2003.10.013
Wu M-N, Juang P-A, Li Y-C: An efficient VQ-based data hiding scheme using voronoi clustering. Proceedings of the 9th International Conference on Hybrid Intelligent Systems (HIS '09), August 2009, Shenyang, China 73-77.
Zhang X, Wang S: Analysis of parity assignment steganography in palette images. Proceedings of the Knowledge-Based Intelligent Information and Engineering Systems, 2005, Lecture Notes in Computer Science 3683: 1025-1031.
Zhang X, Wang S, Zhou Z: Multibit assignment steganography in palette images. IEEE Signal Processing Letters 2008, 15: 553-556.
Brisbane G, Safavi-Naini R, Ogunbona P: High-capacity steganography using a shared colour palette. IEE Proceedings: Vision, Image, and Signal Processing 2005, 152(6):787-792. 10.1049/ip-vis:20045047
Seppannen T, Makela K, Keskinarkaus A: Hiding information in color images using small color palettes. Proceedings of the 3rd International Workshop on Information Security, 2000, Wollongong, Australia 69-81.
Jain AK, Murty MN, Flynn PJ: Data clustering: a review. ACM Computing Surveys 1999, 31(3):316-323.
Fredrich J, Goljan M: Practical steganalysis of digital images: state of the art. Security and Watermarking of Multimedia Contents IV, January 2002, San Jose, Calif, USA, Proceedings of SPIE 4675: 1-13.
Pevný T, Fridrich J: Multiclass detector of current steganographic methods for JPEG format. IEEE Transactions on Information Forensics and Security 2008, 3(4):635-650.
Xuan G, Shi YQ, Gao J, Zou D, Yang C, Zhang Z, Chai P, Chen C, Chen W: Steganalysis based on multiple features formed by statistical moments of wavelet characteristic functions. In Proceedings of the 7th Information Hiding Workshop, June 2005, Barcelona, Spain, Lecture Notes in Computer Science. Volume 3727. Springer; 262-277.
Katzenbeisser S, Petitcolas FAP (Eds): Information Hiding Techniques for Steganography and Digital Watermarking. Artech House Books, Norwood, Mass, USA; 1999.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, CT., Li, Y. Progressive Exponential Clustering-Based Steganography. EURASIP J. Adv. Signal Process. 2010, 212517 (2010). https://doi.org/10.1155/2010/212517
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/212517

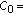 The set of colours in
The set of colours in 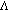 with their orders randomised according to secret key
with their orders randomised according to secret key 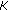 (each individual colour is seen as a cluster);
(each individual colour is seen as a cluster); ;
;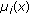 of each cluster
of each cluster 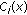 in
in  ;
; ;
;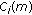 in
in 
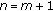 to
to 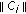
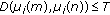
 ;
; (Note "\" is the operation of Set Difference)
(Note "\" is the operation of Set Difference) (At the final iteration,
(At the final iteration,  is either 0 or 1 depending on Step
is either 0 or 1 depending on Step  )
)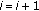 ;
; ;
;
 (the number of pixels with their colours belonging to
(the number of pixels with their colours belonging to  );
);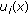 of cluster
of cluster 
 of Inequality (5);
of Inequality (5);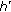 according to (7);
according to (7);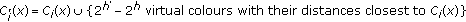 . Note
. Note into binary form;
into binary form;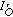 is not raeached
is not raeached is the only member of its cluster
is the only member of its cluster  (i.e., this pixel is non-embeddable)
(i.e., this pixel is non-embeddable)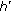 (
( )?bits from
)?bits from  , denoted as
, denoted as 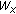 ;
;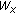 th colour in
th colour in  ;
; based on
based on 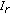 ; (Note no cluster expansion is needed.)
; (Note no cluster expansion is needed.)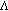 to get the cluster configuration
to get the cluster configuration 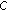 using the same threshold
using the same threshold 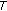 and the shared secret key
and the shared secret key 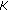 ;
;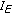 is not reached
is not reached is the only member of its cluster
is the only member of its cluster 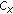 (i.e.,
(i.e.,  is non-embeddable)
is non-embeddable) ;
; of the colour in
of the colour in 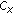 into binary form;
into binary form;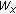 to the binary stream of the secret data
to the binary stream of the secret data 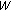 extracted so far;
extracted so far;








 -Secure
-Secure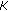 and distance threshold
and distance threshold  . Sharing the large colour palette and the centroids of the clusters (as required in [
. Sharing the large colour palette and the centroids of the clusters (as required in [