- Research Article
- Open access
- Published:
A Method for Counting Moving People in Video Surveillance Videos
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 231240 (2010)
Abstract
People counting is an important problem in video surveillance applications. This problem has been faced either by trying to detect people in the scene and then counting them or by establishing a mapping between some scene feature and the number of people (avoiding the complex detection problem). This paper presents a novel method, following this second approach, that is based on the use of SURF features and of an  -SVR regressor provide an estimate of this count. The algorithm takes specifically into account problems due to partial occlusions and to perspective. In the experimental evaluation, the proposed method has been compared with the algorithm by Albiol et al., winner of the PETS 2009 contest on people counting, using the same PETS 2009 database. The provided results confirm that the proposed method yields an improved accuracy, while retaining the robustness of Albiol's algorithm.
-SVR regressor provide an estimate of this count. The algorithm takes specifically into account problems due to partial occlusions and to perspective. In the experimental evaluation, the proposed method has been compared with the algorithm by Albiol et al., winner of the PETS 2009 contest on people counting, using the same PETS 2009 database. The provided results confirm that the proposed method yields an improved accuracy, while retaining the robustness of Albiol's algorithm.
1. Introduction
The estimation of the number of people present in an area can be an extremely useful information both for security/safety reasons (for instance, an anomalous change in the number of persons could be the cause or the effect of a dangerous event) and for economic purposes (for instance, optimizing the schedule of a public transportation system on the basis of the number of passengers). Hence, several works in the fields of video analysis and intelligent video surveillance have addressed this task.
The problem of people counting has been faced using two different approaches. In the direct approach (also called detection based), people in the scene are first individually detected, using some form of segmentation and object detection, and then counted. In the indirect approach (also called map based or measurement based), instead, counting is performed using the measurement of some feature that does not require the separate detection of each person in the scene. The indirect approach is considered to be more robust, since the correct segmentation of people in the scene is by itself a complex problem that cannot be solved reliably, especially in crowded conditions.
Recent examples of the direct approach are [1–3]. In [1], the shape of a standing person is modeled as a rectangle of fixed width and height (normalized on the basis of perspective mapping). The system first detects foreground regions using background subtractions and then tries to match people models with the observed edges of foreground regions, using a global optimization technique based on the Expectation-Maximization algorithm. While the method is able to deal with partially occluded persons, the assumption that the foreground region contour contains enough edges that can be ascribed to each person limits the applicability of the method to cases where the density of the crowd is low. In [2], the tracking of feature points is performed first, and then the points are grouped into objects according to their motion characteristics. Namely, feature points are extracted using methods from the literature and are tracked using a combination of optical flow and searching in a 2D window around the previous feature position. Then, the feature points are clustered using a Bayesian framework, under the assumption that pairs of points belonging to a same person have a small variance in their mutual distance (quasi-rigid motion). While the method seems to perform well, even with high crowd densities, when the motion is mainly parallel to the image plane, it has problems with motion directed towards the camera or away from it. Also, the method can have problems in low density conditions, where the motion of arms and legs is clearly visible, because of its rigid motion assumption. In [3], a 3D model of the human body is used. Each person is represented as a set of ellipsoids corresponding to the head, the body and the legs. The model is matched to the detected foreground regions using a Markov Chain Monte Carlo (MCMC) approach, that performs a global optimization of the a posteriori probability across multiple frames (in order to exploit temporal coherence). While the method provides good performance with low to medium crowd densities, it could have problems in very crowded scenes. Furthermore, it is very computationally intensive, being impractical for real-time applications.
For the indirect approach, recent methods have proposed, among the others, the use of measurements such as the amount of moving pixels [4], blob size [5], fractal dimension [6], or other texture features [7].
A recent method following the indirect approach has been proposed by Albiol et al. in [8]. This method has been submitted to the PETS 2009 contest on people counting, and has obtained the best performance among the contest participants. In Albiol's paper, the authors propose the use of corner points as features. Namely, corner points are found using a variant of the popular Harris corner detector [9]. Then, background corner points are separated from foreground corner points using an estimate of the motion vector based on block matching between adjacent frames: points whose motion speed is under a threshold are not considered for further analysis. Finally, the number of people is estimated from the number of moving corner points assuming a direct proportionality relation, with a constant factor determined using a frame of the video sequence. Actually, the count so obtained is smoothed by averaging along a few adjacent frames to remove fluctuations due to noise.
Although the assumptions underlying Albiol's paper may appear rather simplistic, the method has proven to be quite more robust than more sophisticated competitors. However, the accuracy it can attain is limited by the fact that it does not take into account problems like the instability of the Harris corner detector, the presence of occlusions, or the need of a perspective correction.
In this paper we propose a method that, while retaining the overall simplicity and the robustness of Albiol's approach, tries to provide a more accurate estimation of the count by considering also these factors.
2. Rationale of the Proposed Method
The approach we propose in this paper is conceptually similar to the one proposed by Albiol et al. [8] but introduces several changes to overcome some limitations of that method.
The first problem that is addressed is the stability of detected corner points. The points found by the Harris corner detector are strongly dependent on the perceived scale of the considered object: the same object, even in the same pose, will have different detected corners if its image is acquired from different distances. This can cause problems in the following conditions:
-
(i)
the observed scene contains groups of people whose distance from the camera is very different: in this case it is not possible to use a simple proportionality to estimate the number of people, since the average number of corner points per person is different between close people and far people,
-
(ii)
the observed scene contains people walking on a direction that has a significant component orthogonal to the image plane, that is, they are coming closer to the camera or getting farther from it: in this case the number of corner points for these people is changing even if the number of people remains constant.
To mitigate this problem we have chosen to adopt the SURF algorithm proposed by Bay et al. in [10]. SURF is inspired by the SIFT scale-invariant descriptor [11], but replaces the Gaussian-based filters of SIFT with filters that use the Haar wavelets, which are significantly faster to compute. The interest points found by SURF are much more independent of scale (and hence of distance from camera) than the ones provided by Harris detector. They are also independent of rotation, which is important for the stability of the points located on the arms and on the legs of the people in the scene.
A second limitation in Albiol's method is that it does not take into account the density of the detected interest points in the estimation of the number of people. To understand why this can be a problem, it has to be considered that the amount of occlusions in the image of a group of people depends on how close the people are to each other. If people are distant from each other, occlusion is unlikely and all the interest points of a person shape are detected; on the other hand, if people are very close to each other, it is likely that most of the body of each person is occluded by others, and so only a subset of the corresponding interest points are detected. Hence, the average number of points per person can vary significantly with the people density.
We use the interest point density as a way to estimate the people density. However, a naive use of this measure would present a problem: because of perspective distortion, the same people density would correspond to a different point density at different distances from the camera. So a correction of the perspective distortion is needed.
To perform this task, we have first to partition the detected points into groups corresponding to different groups of people. This can be treated as a clustering problem, but the shape of the clusters, their number and their densities are not known a priori, and so commonly used clustering algorithms such as k-means and DBSCAN cannot be applied. So we have adopted a graph-based clustering algorithm presented in [12]. The point density of each cluster can be estimated by dividing the number of points in the clusters by the area of the bounding box of the cluster; this approximation works well in practice, but if more precision was needed, it could be achieved by computing the convex hull of the cluster and dividing the number of points by its area.
Once the detected points are divided into clusters, the distance of each cluster from the camera is derived from the position of the bottom points of the cluster applying an Inverse Perspective Mapping (IPM). The IPM is based on the assumption that the bottom points of the cluster lie on the ground plane. So it is possible, using an inverse perspective matrix, to map the image coordinates of the points to real-world, 3D coordinates in the scene. The inverse perspective matrix can be derived by calibration, using the images of several persons located at different distances from the camera and assuming that they have an average height. Once the actual distance from the camera is known, the average density of the points within the cluster is normalized to the value it would have if the cluster was moved to a predetermined distance from the camera.
The third limitation that is addressed by our method is that the relation between the number of detected points and the number of people can have a form that is more complex than a simple direct proportionality, especially if we take into account the point density. So we have chosen to learn this relation by using a trainable function estimator. More precisely, we have used a variation of the Support Vector Machine known as  -Support Vector Regressor (
-Support Vector Regressor ( -SVR for short) as our function estimator. The
-SVR for short) as our function estimator. The  -SVR receives as its inputs the number of points of a cluster and the (normalized) density, and is trained (using a set of training frames) to output the estimated number of people in the cluster. The
-SVR receives as its inputs the number of points of a cluster and the (normalized) density, and is trained (using a set of training frames) to output the estimated number of people in the cluster. The  -SVR is able to learn a nonlinear relation and shows a good generalization ability, being based on the structural risk minimization principle.
-SVR is able to learn a nonlinear relation and shows a good generalization ability, being based on the structural risk minimization principle.
As with Albiol's method, the output count is passed through a low-pass filter to smooth out oscillations due to image noise.
3. System Architecture
The overall system architecture of the proposed algorithm for people counting is shown in Figure 1.
As delineated in the previous section, the system operates according to the three phases reported below:
-
(1)
detection of the interest points associated to people,
-
(2)
clustering of the interest points,
-
(3)
features extraction and regression.
In the following we provide some details about each of the considered phases.
3.1. Detection of the Interest Points Associated to People
In order to detect interest points associated to people we make two basic assumptions: persons within the scene are not static and there are no other moving elements in the scene. Thus, if we compute the interest points of the image and the associated motion information, the above assumptions guarantee that only the interest points with a non-null motion vector must be associated to people.
Note that the first assumption holds very often: in fact, although a person might appear static, some motion, even very small, is usually associated to her/him. The second assumption stands in most real world applications where it is required to count people in the scene; of course in the rare cases in which the second assumption is not verified (waving trees, moving vehicles, etc.), the proposed method cannot be adopted.
As proposed in [8], the interest points associated to people are extracted in two steps. First, we determine all the interest points within the frame under analysis. Then, we prune the points not associated to persons by taking into account their motion information.
Interest points are determined by using the SURF algorithm [10] and not the Harris corner detector as in the paper by Albiol et al. [8]. As widely described in the previous Section, the motivation behind this choice is that the interest points extracted using SURF are scale-invariant, thus they are much more stable than the points found by the Harris corner detector.
In order to remove the static interest points (that are not associated to people), for each point detected by the SURF algorithm we estimate the motion vector with respect to the previous frame by using a block-matching technique. Then we distinguish between static and moving interest points on the basis of the following rule:

where  is the interest point at the
is the interest point at the  coordinates,
coordinates,  is the magnitude of the motion vector calculated in
is the magnitude of the motion vector calculated in  with respect to the previous frame, and
with respect to the previous frame, and  is a bias value (in our experiments we set
is a bias value (in our experiments we set  ).
).
Unfortunately motion vectors are only relatively reliable. Occlusions, sudden changes in illumination, artifacts introduced by the compression of the video stream, may cause errors in the estimations of motion vectors. Although we are not interested to the exact value of the motion vectors, but only to distinguish between null and non-null vectors, the low reliability of their estimation has to be taken into proper account. In Figure 2 it is shown an example of the points detected using the SURF algorithm and the corresponding motion vectors. The moving interest points are depicted in green, while the static ones are in red. It should be noted that a not negligible percentage (in our experiments about 10%) of the interest points were erroneously classified as moving points. The presence of these spurious points may cause an overestimation of the number of the persons in the scene. However, these outliers are usually randomly spread throughout the frame. This spatial distribution makes their removal easier if carried out in the second stage of the system, where we try to cluster the interest points. It is also worth noting that the occurrence of the other type of error, that is, a moving point classified as static, is minimal; thus, this sort of error does not affect significantly the overall performance of the system and no specific procedure has been devised to tackle it.
3.2. Clustering of the Interest Points
In order to compensate for changes in the number of points due to perspective and to partial occlusions, the algorithm needs to partition the detected points into clusters corresponding to separated groups of persons, so as to be able to compute for each group its distance from the camera and its density.
The faced clustering problem is characterized by the fact that we do not have any a priori knowledge about the number and the shape of the clusters to be found. This depends on the fact that people can appear in different positions in the scene and can be aggregated in many different ways. In this situation more commonly used clustering methods (such as k-means) could not have been applied because they require the user to provide either the number of desired clusters or a threshold on cluster diameter or on intercluster distance. As observed in [13], the clustering algorithms based on graph theory are well suited to face clustering problems where no assumptions can be made about the clusters. In particular, we adopted the technique presented in [12], since (differently from other algorithms in the graph-based clustering family) it requires no parameters to be tuned or adapted to the particular application.
This algorithm represents the set of points as a graph in which each point corresponds to a node and each edge is labeled with the distance between its endpoints. The minimum spanning tree (MST) of the graph is computed; this tree will contain some edges that are between nodes in the same cluster (intracluster edges) and other edges between nodes of different clusters (intercluster edges). Assuming that the clusters are well separated, it can be expected that the intracluster edges are shorter than the intercluster edges. So the algorithm uses a thresholding to divide the edges in two sets (the ones below the threshold, say it  , and the ones above the threshold
, and the ones above the threshold  ). The edges in the second set are deleted, and the remaining connected components are the clusters output by the algorithm.
). The edges in the second set are deleted, and the remaining connected components are the clusters output by the algorithm.
The use of a fixed value for the threshold  would be problematic, since the threshold would need to be adjusted depending on the resolution, the distance from the camera and so on. Instead, we have used a threshold proportional to the average edge length, computed as
would be problematic, since the threshold would need to be adjusted depending on the resolution, the distance from the camera and so on. Instead, we have used a threshold proportional to the average edge length, computed as

where  is the proportionality factor,
is the proportionality factor,  is the number of edges of the spanning tree, while
is the number of edges of the spanning tree, while  is the weight of the
is the weight of the  th edge of the tree. We have experimentally found that the choice
th edge of the tree. We have experimentally found that the choice  works adequately for all the considered scenes.
works adequately for all the considered scenes.
In the ideal case, all the intracluster edges are preserved, while the intercluster edges are removed, leaving a set of connected trees corresponding to the desired clusters of interest points. However, it commonly happens that some edges are misclassified producing two types of clustering errors.
(1) Inter-Cluster Edges Classified as Intra-Cluster
This type of misclassification does not allow to split some clusters, which will result aggregated. However, this situation does not represent a problem when the joined clusters refer to groups of people which are at the same distance from the camera. This typically happens when the clusters are horizontally aggregated (see the example in Figure 3(a)). In fact, in this case the perspective distortion does not change significantly among the joined clusters and the error introduced can be considered negligible. Conversely, when the erroneously combined clusters refer to groups of people at different distances from the camera (typically when clusters are joined vertically), this causes errors in the estimation of the number of people which are inside the groups whose distance from the camera is erroneously evaluated (see the box with ID = 2 in Figure 4(b) for an example of this problem). It is worth noting that even if the estimation for clusters formed by people at different distances may be inaccurate, it is still an improvement over the use of a global estimate based on all the detected points in the scene, as in Albiol et al.'s method. Furthermore, we have experimentally verified that the latter circumstance occurs rather infrequently, hence its impact on the overall performance is limited.
Clusters of point detected by the second stage of the system. Each cluster is enclosed by a bounding box. The images also contain examples of clustering errors. (a) In cluster 1 (green interest points) two groups of people have been erroneously aggregated. (b) A group of people is erroneously split in two clusters, (yellow and cyan points, clusters 3 and 5).
Effect of perspective distortion on the number of detected interest points: note how the same woman in (a) is far from the camera (cluster 0, red dots) and only 9 interest points are detected, while in (b) she is closer to the camera (cluster 1, green dots) and 30 interest points are associated to her.
(2) Intra-Cluster Edges Classified as Inter-Cluster
This phenomenon causes a cluster to be split into several parts. Similar considerations can be done also for this type of error as regard the different incidence and impact on the overall performance depending on the way the splits occur (horizontal or vertical). An example of this type of error is shown in Figure 3(b).
Another important problem that is faced in this stage is represented by the removal of outliers, that is, those interest points which are output by the previous stage but are not associated to people. It is quite easy to distinguish between the correct moving points and the outliers, on the basis of some considerations about the local point density. In fact, while the points associated to people are concentrated in small areas in the input image (those occupied by the persons), erroneously detected moving points are randomly spread throughout the frame. Consequently, after clustering the outliers tend to form singleton or very small isolated clusters, which can be simply cut off by adopting a procedure that deletes those clusters with a number of points below a fixed threshold. At least in principle, this threshold may depend on the position and angle of the camera and on some peculiarities of the environment. However, in our experiments (which include different scenes and view points) we set it to eight and noticed that the value of this threshold can vary in a quite wide range without affecting significantly the overall performance of the system.
3.3. Feature Extraction and Regression
In this stage of the algorithm, a feature vector is computed from each cluster detected in the previous step, and is fed into a regressor. The output of the regressor is the estimated number of persons in the group represented by the cluster.
The basic idea of the method in [8] is that the average number of interest points associated to each person is a global property of scene. Thus, once the scene has been defined, it is possible to assume a simple direct proportionality relation between the number of points and the number of persons.
As noted by the same authors in [8], this model, albeit extremely simple, performs well in scenes where people are more or less at the same distance from the camera, and there are only limited overlaps between persons. When these assumptions are verified, deviations from the model are either due to the fact that some interest points are missed (e.g., because a part of body is very similar to the underlying background) or due to the limited reliability of motion vector estimation, that may cause some static points to be considered as moving.
However, as can be deducted from the good performance shown by Albiol's method on the PETS2009 dataset, those deviations from the model often compensate each other, and so the method gives a reasonable count, at least on the average.
Unfortunately, this model does not take into account the effects of the perspective, which causes that the farther the person is from the camera, the fewer are the detected interest points (see Figure 4 for an example of this problem). Hence, the number of points associated to a person and the distance of the person from the camera are somehow related, and the relation is nonlinear.
Moreover, the assumption of a proportionality relation between the number of persons and the number of points holds only when people are well separated from each other. On the other hand, when people are close to each other some parts of their bodies are occluded and, consequently, some interest points are not detected. Therefore, there is a relation (whose exact form is not easy to find analytically) also between the average number of points per person and the people density. Unfortunately, we do not know the people density of each cluster. However we can reasonably assume that when the density of people increase, the detected points get closer to each other. So we can consider the density of the points as related to people density, and we can indirectly take into account people density by establishing a relation between the average number of points per person and the point density.
In conclusion, the relation between the number of interest points and the number of people appears more complex than a direct proportionality, as we have to take into account also the distance of the people from the camera and the point density. We can formulate this relation as

where
-
(i)
 is the estimated number of people;
is the estimated number of people; -
(ii)
 is the number of interest points within the cluster;
is the number of interest points within the cluster; -
(iii)
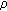 is the average density of the points in the cluster: the value is obtained as the ratio between the number of points into the cluster and the area of the bounding box. Note that the area of the bounding box is computed with respect to real world coordinates. This allows us to normalize the average density of the points to the value it would have if the cluster were moved to a predefined distance from the camera;
is the average density of the points in the cluster: the value is obtained as the ratio between the number of points into the cluster and the area of the bounding box. Note that the area of the bounding box is computed with respect to real world coordinates. This allows us to normalize the average density of the points to the value it would have if the cluster were moved to a predefined distance from the camera; -
(iv)
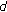 is the distance of the cluster from the camera: assuming that the bottom points of the bounding box lie on the ground plane, the calculation is done by applying an Inverse Perspective Mapping and is referred to the center of the bottom edge of the cluster's bounding box.
is the distance of the cluster from the camera: assuming that the bottom points of the bounding box lie on the ground plane, the calculation is done by applying an Inverse Perspective Mapping and is referred to the center of the bottom edge of the cluster's bounding box.
Since we do not know the analytical form of  , we have chosen to learn this function from a set of labeled examples by using an
, we have chosen to learn this function from a set of labeled examples by using an  -SVR regressor. Once trained, the
-SVR regressor. Once trained, the  -SVR acts as a function estimator; for each detected cluster it receives as its input the above features and outputs the estimated number of people within the cluster. So the total number of persons in the frame (or in a predetermined region of interest) is obtained by summing the number of people calculated for each cluster.
-SVR acts as a function estimator; for each detected cluster it receives as its input the above features and outputs the estimated number of people within the cluster. So the total number of persons in the frame (or in a predetermined region of interest) is obtained by summing the number of people calculated for each cluster.
Finally, in order to smooth out the oscillations in the number of the counted persons among consecutive frames, we employ a low-pass filter. Specifically, the final count of the persons within the scene is calculated as the average value of the people count on the last k frames of the video.
4. Experimental Results
The performance of the proposed method has been assessed using the PETS2009 dataset [14]. The dataset is organized in four sections, but we focused our attention primarily on the section named S1 that was used to benchmark algorithms for the "Person Count and Density Estimation" PETS2009 contest. The main characteristics of the subset of video sequences of the PETS 2009 dataset used for assessing the performance of the proposed method are summarized in the Table 1 in terms of their length, number of people in the scene (minimum, maximum and average number) and other elements as density of the crowd, illumination conditions, and so forth. The videos reported in Table 1 refer to two different views obtained by using two cameras that contemporaneously framed the same scene from different points (see Figure 5 for example frames of the two views). For our experimentations, we used four videos of the view 1, which are also the same videos that were used in the people counting contest held in PETS2009. The videos in the second set refer to the view 2 which is characterized by a wide field depth that makes the counting problem more difficult to solve.
For all the sequences we calculated the number of people in the whole frame.
In order to use the proposed system for people counting, we had first to train the  -SVR regressor. The minimum size of the training set needed to achieve an acceptable performance, as the statistical learning theory by Vapnik and Chervonenkis has demonstrated, depends on both the complexity of the problem and the complexity of the estimator to be trained. The method by Albiol et al. uses a very simple estimator, so that a single frame per sequence is sufficient for the training. Our estimator is more complex, so it needs more training frames. The training set was built by manually collecting some samples of people groups from a subset of the test frames. For each selected box we calculated the feature vector and the associated ground truth, that is, the true number of persons that are inside the box. Samples were carefully selected in order to guarantee that all the possible combinations in terms of number of persons in the group, points density and distance from the camera were adequately represented in the training set. It is worth pointing out that the required number of training frames has not to be very large to achieve a good performance level (in our tests we used about 30–40 training frames), by taking into account also the fact that a single frame usually contains several people clusters at different distances, so it may cover several cases of the function to be learned.
-SVR regressor. The minimum size of the training set needed to achieve an acceptable performance, as the statistical learning theory by Vapnik and Chervonenkis has demonstrated, depends on both the complexity of the problem and the complexity of the estimator to be trained. The method by Albiol et al. uses a very simple estimator, so that a single frame per sequence is sufficient for the training. Our estimator is more complex, so it needs more training frames. The training set was built by manually collecting some samples of people groups from a subset of the test frames. For each selected box we calculated the feature vector and the associated ground truth, that is, the true number of persons that are inside the box. Samples were carefully selected in order to guarantee that all the possible combinations in terms of number of persons in the group, points density and distance from the camera were adequately represented in the training set. It is worth pointing out that the required number of training frames has not to be very large to achieve a good performance level (in our tests we used about 30–40 training frames), by taking into account also the fact that a single frame usually contains several people clusters at different distances, so it may cover several cases of the function to be learned.
Testing has been carried out by comparing the actual number of people in the video sequences and the number of people calculated by the algorithm. The indices used to report the performance are the Mean Absolute Error (MAE) and the Mean Relative Error (MRE) defined as

where  is the number of frames of the test sequence and
is the number of frames of the test sequence and  and
and  are the guessed and the true number of persons in the
are the guessed and the true number of persons in the  -th frame, respectively.
-th frame, respectively.
The MAE index is the same performance index used also to compare the performance of the algorithms that participated to the PETS2009 contest. This index is very useful to exactly quantify the error in the estimation of the number of person which are in the focus of the camera, but it does not relate this error to number of people; in fact, the same absolute error can be considered negligible if the number of persons in the scene is high while it becomes significant if the number of person is of the same order of magnitude. For this reason, we introduced also the MRE index which takes into account the estimation error related to the true people number.
The performance of the proposed method on the adopted dataset is reported together with that of Albiol's method, for which we have provided our own implementation. The motivation behind the choice of comparing our technique with respect to Albiol's method is twofold. First, it constitutes the base from which we started for the definition of our method; thus, the comparison allows us to quantify the improvement provided by the proposed modifications. Secondly, Albiol's method has already been compared to other algorithms based either on the direct or the indirect approach, in the PETS 2009 contest on people counting, and has consistently outperformed them. Since our test dataset contains also the video sequences used for the PETS 2009 contest on people counting, we can reasonably expect that, at least on that kind of scene, also our method should show an improvement over those other algorithms.
It is worth noting that also Albiol's method requires a training procedure for determining the optimal value of the interest points per person ratio. This value was determined by minimizing the MAE on the same set of frames already used for training our method.
From the results reported in Table 2 it is evident that the proposed method always outperforms Albiol's technique with respect to both MAE and MRE performance indices.
In order to have a deeper insight into the behavior of the considered algorithms, Figure 6 shows the estimated number of people with respect to time for both our algorithm and Albiol's over two video sequences.
The different behavior of the considered algorithms can be explained by considering that Albiol's method hypothesizes a linear relation between the number of detected interest points and the number of persons without taking into account the perspective effects and the people density. As a result this method provides better results when it is tested on videos characterized by conditions that are similar to those present in the training videos. Conversely, the proposed method is more robust with respect to the above problems.
In particular, the Figure 6(a) refers to the view 1 of the video sequence S1.L1.13-59: this video is characterized by a group of persons that gradually enters and crosses the scene. In this view all the persons move in a direction that is orthogonal to the optical axis of the camera, so that their distance from the camera does not change significantly during their permanence in the scene. Consequently the main contribution to the performance improvement provided by our method can be ascribed to the fact that it takes into account the problem of the occlusions of the persons by means of points density. In fact, from the figure it is possible to note that the higher is the number of people, the higher is the estimation error of the method of Albiol.
In Figure 6(b), that refers to the view 2 of the sequence S1.L1.13-57, the persons move in a direction that is almost parallel to the optical axis of the camera; thus in this case the correction of the perspective effects plays a fundamental role in the performance improvements obtained by the proposed method. In fact, in this case the method of Albiol et al. tends to overestimate or underestimate the number of persons when they are close to or far from the camera while it provides a good estimate only when the persons are at an average distance from the camera (this is evident by considering Albiol and the ground truth curves in the figure). On the contrary the proposed method is able to keep the estimation error low along almost all the sequence. The exception is represented by the last part of the sequence where the method tends to underestimate the number of the person: however, this can be explained by considering that in this part of the video the persons are very far from the camera and most of their interest points are considered static.
In Table 3 we have reported the performance changes only due to the replacement of Harris corner detector with SURF. As it could be expected, SURF gives a consistent performance improvement on the videos corresponding to view 2, where the persons appear at different distances from the camera; in this case the SURF approach provides points that are less sensitive to the scale at which a person is perceived. On the other hand, for view 1 (where all the persons are at about the same distance from the camera) Harris detector gives the best results, since its greater simplicity makes it slightly more robust to image noise; however, the flexibility of the trainable  -SVR regressor is able to compensate for this weakness of the SURF detector.
-SVR regressor is able to compensate for this weakness of the SURF detector.
5. Conclusions
In this paper, we have proposed a novel method for counting moving people in a video surveillance scene. The method has been compared, both theoretically and experimentally, with the algorithm by Albiol et al. that was the winner of the PETS 2009 contest on people counting, highlighting the effectiveness of its enhancements. The experimentation on the PETS 2009 database has confirmed that the proposed method is in several cases more accurate than Albiol's but retains a comparable robustness that is considered the greatest strength of the latter. As a future work, a more extensive experimentation will be performed, adding other algorithms to the comparison and enlarging the video database to provide a better characterization of the advantages of the new algorithm.
References
Rittscher J, Tu PH, Krahnstoever N: Simultaneous estimation of segmentation and shape. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '05), June 2005 486-493.
Brostow GJ, Cipolla R: Unsupervised bayesian detection of independent motion in crowds. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '06), June 2006 594-601.
Zhao T, Nevatia R, Wu B: Segmentation and tracking of multiple humans in crowded environments. IEEE Transactions on Pattern Analysis and Machine Intelligence 2008, 30(7):1198-1211.
Cho S-Y, Chow TWS, Leung C-T: A neural-based crowd estimation by hybrid global learning algorithm. IEEE Transactions on Systems, Man, and Cybernetics, Part B 1999, 29(4):535-541. 10.1109/3477.775269
Kong D, Gray D, Tao H: A viewpoint invariant approach for crowd counting. Proceedings of the 18th International Conference on Pattern Recognition (ICPR '06), August 2006 1187-1190.
Marana AN, Costa LDAF, Lotufo RA, Velastin SA: Estimating crowd density with Minkowski fractal dimension. Proceedings of the 1999 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '99), March 1999 3521-3524.
Rahmalan H, Nixon MS, Carter JN: On crowd density estimation for surveillance. Proceedings of the The Institution of Engineering and Technology Conference on Crime and Security, 2006
Albiol A, Silla MJ, Albiol A, Mossi JM: Video analysis using corner motion statistics. Proceedings of the IEEE International Workshop on Performance Evaluation of Tracking and Surveillance, 2009 31-38.
Harris C, Stephens M: A combined corner and edge detector. Proceedings of the Proceedings of the 4th Alvey Vision Conference, 1988 147-151.
Bay H, Ess A, Tuytelaars T, Van Gool L: Surf: speeded-up robust features (SURF). Computer Vision and Image Understanding 2008, 110(3):346-359. 10.1016/j.cviu.2007.09.014
Lowe DG: Distinctive image features from scale-invariant keypoints. International Journal of Computer Vision 2004, 60(2):91-110.
Foggia P, Percannella G, Sansone C, Vento M: A graph-based algorithm for cluster detection. International Journal of Pattern Recognition and Artificial Intelligence 2008, 22(5):843-860. 10.1142/S0218001408006557
Theodoridis S, Koutroumbas K: Pattern Recognition. 3rd edition. Academic Press, New York, NY, USA; 2006.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Conte, D., Foggia, P., Percannella, G. et al. A Method for Counting Moving People in Video Surveillance Videos. EURASIP J. Adv. Signal Process. 2010, 231240 (2010). https://doi.org/10.1155/2010/231240
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/231240




 is the estimated number of people;
is the estimated number of people; is the number of interest points within the cluster;
is the number of interest points within the cluster;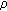 is the average density of the points in the cluster: the value is obtained as the ratio between the number of points into the cluster and the area of the bounding box. Note that the area of the bounding box is computed with respect to real world coordinates. This allows us to normalize the average density of the points to the value it would have if the cluster were moved to a predefined distance from the camera;
is the average density of the points in the cluster: the value is obtained as the ratio between the number of points into the cluster and the area of the bounding box. Note that the area of the bounding box is computed with respect to real world coordinates. This allows us to normalize the average density of the points to the value it would have if the cluster were moved to a predefined distance from the camera;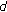 is the distance of the cluster from the camera: assuming that the bottom points of the bounding box lie on the ground plane, the calculation is done by applying an Inverse Perspective Mapping and is referred to the center of the bottom edge of the cluster's bounding box.
is the distance of the cluster from the camera: assuming that the bottom points of the bounding box lie on the ground plane, the calculation is done by applying an Inverse Perspective Mapping and is referred to the center of the bottom edge of the cluster's bounding box.

 -axis it is reported the frame number.
-axis it is reported the frame number.