- Research Article
- Open access
- Published:
Synchronization between EMG at Different Uterine Locations Investigated Using Time-Frequency Ridge Reconstruction: Comparison of Pregnancy and Labor Contractions
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 242493 (2010)
Abstract
The extraction of the frequency components of a signal can be useful for the characterization of the underlying system. One method for isolating a frequency component of a signal is by the extraction and reconstruction of the local maxima or ridge of its time-frequency representation. We compare here the performances of two well-known ridge reconstruction methods, namely the Carmona and Marseille methods, on synthetic signals as well as real electrohysterogram (EHG). We show that Carmona's method presents lower reconstruction errors. We then used the separately reconstructed frequency components of the EHG independently for labor prediction using a synchronization measure. We show that the proposed synchronization parameters present similar prediction rate to classical parameters obtained directly from the time-frequency representation but also seem to provide information complementary to the classical parameters and may thus improve the accuracy in labor prediction when they are used jointly.
1. Introduction
Preterm labor is an important public health problem in Europe and other developed countries as it represents nearly 7% of all births. It is the main cause of morbidity and mortality of newborns. One of most promising biophysical markers of preterm labor threat is the electrical activity of the uterus, the uterine electromyogram [1]. The uterine electromyogram recorded externally in women, the electrohysterogram (EHG), has been proven to be representative of uterine contraction. The analysis of such a signal may allow the prediction of preterm labor as soon as the 28th week of gestation (WG) [2, 3]. However, the physiological phenomena underlying preterm labor remain poorly understood. It is well known that uterine contractility depends on the excitability of uterine myocytes, but also on the propagation of the electrical activity to the whole uterus [4]. These two aspects of uterine contraction mechanisms, excitability and propagation, both influence the spectral content of EHG. The methods proposed in the literature for preterm labor prediction most often use only the analysis of the high frequency content of the EHG which is thought to be primarily related to excitability [1, 5, 6]. These methods are however not currently used in routine practice due to a high variance of the results obtained and an insufficient prediction rate. Taking into account both the excitability and propagation information may help to increase the prediction capability of the EHG for preterm labor threat identification.
Recent work by us and others has concentrated on providing good measures of the increase in the propagation of the activity in the uterus associated to the advance of pregnancy [7–9]. The propagation capability of the uterus cannot be measured as a classical propagation speed, as it is usually done for skeletal muscles, but must be estimated through synchronization measures. The synchronization of different parts of the uterus at term is thought to be related to the presence of gap junction making possible direct communications between adjacent myocytes. The number of gap junction is known to increase as labor approaches and is a necessary step for obtaining an uterus that is working as a whole, in order to produce forceful contractions during delivery [10, 11].
EHG is mainly composed of two frequency components traditionally referred to as FWL (Fast Wave Low) and FWH (Fast Wave High) [4]. These frequency components may be related, respectively, to the propagation and to the excitability of the uterus. This hypothesis has however not yet been conclusively verified or rejected. A possible way of addressing this question, as well as an avenue in to using propagation phenomenon in the prediction of preterm labor, may very well be to extract FWL using ridge reconstruction methods and to characterize it separately.
The GVF-Snake method has been recently identified as an appropriate method for EHG ridge extraction [12]. This technique has been successfully used for the characterization of human EHG recorded during labor directly in the time-frequency domain [13]. Although we consider the GVF-Snake extraction method to be very good for EHG applications, the most appropriate method for reconstructing the EHG signal from time-frequency ridges has however not yet been identified. In this paper we investigate the performances of two methods, the Marseille and Carmona's methods, in this context. Identifying a good method to do this opens a door for characterizing the frequency components of the EHG separately in order to define new parameters for pregnancy monitoring. In this paper we use a synchronization measure, the  nonlinear correlation coefficient, to illustrate this point.
nonlinear correlation coefficient, to illustrate this point.
The problem addressed in this paper is thus twofold: to find an excellent ridge reconstruction method to separate the frequency components of the EHG and to find a good measure of the changes in propagation properties in the uterus, as pregnancy contractions evolve into effective labor contractions.
2. Ridge Extraction Methods
The extraction of the frequency components of signals is often a necessary step in order to characterize a system. Several methods could be used in order to perform the component separation in the temporal domain. If the frequency components are linearly separable in the frequency domain, that is, components with no overlapping spectra, simple linear filter could be used. This approach is commonly used for the extraction of the different frequency band of the electroencephalogram (EEG) for example. If the frequency components are not linearly separable, more complex methods have to be used. Among the most popular methods are the empirical mode decomposition (EMD), the fractional Fourier transform and the reconstruction of time-frequency ridges. In our application, the fractional Fourier transform is not suitable since the time-frequency signature of the EHG are highly variable from one burst to another. To apply this method on our signals would thus require defining separate fractional frequencies for each contraction. When applied to the EHG, the EMD method gives many more components (intrinsic mode function, IMF) than FWL and FWH. Moreover the number of components varies from one contraction to another one (preliminary results, unpublished work). Using this method in our application requires a complex IMF selection/fusion algorithm. We therefore chose to focus our paper on the time-frequency ridge extraction/reconstruction approach as the most suitable and promising method at our disposal.
A time-frequency ridge,  , represents continuous local energy maxima in the time-frequency domain. It has been shown that ridges are representative of amplitude and frequency modulated signals [14]. Several algorithms for ridge extraction have been proposed in the literature. The main methods are based on simulating annealing [14], snake [12, 14] or direct search approaches [15]. Particularly for the extraction of the frequency components of the EHG, snake and direct search methods have been used [12, 16, 17]. A comparison of these methods in monkey EHG was done in [12]. The proposed GVF-Snake method has proved to be the most efficient for the analysis of EHG frequency components. It has also been successfully used for the characterization of human contractions recorded during labor [13]. This method is similar to the "Snake Ridge" proposed by Carmona and Hwang [14] but uses GVF formulation for external forces, as proposed by Xu and Prince [18]. GVF-Snake method presents a high attraction range, and is thus less sensitive to inaccurate initialization. From a general point of view, this method can be used successfully on various time-frequency representations even those presenting cross-terms like Wigner-Ville representation [19]. In this paper we used this method for the analysis of synthetic signals as well as real EHG.
, represents continuous local energy maxima in the time-frequency domain. It has been shown that ridges are representative of amplitude and frequency modulated signals [14]. Several algorithms for ridge extraction have been proposed in the literature. The main methods are based on simulating annealing [14], snake [12, 14] or direct search approaches [15]. Particularly for the extraction of the frequency components of the EHG, snake and direct search methods have been used [12, 16, 17]. A comparison of these methods in monkey EHG was done in [12]. The proposed GVF-Snake method has proved to be the most efficient for the analysis of EHG frequency components. It has also been successfully used for the characterization of human contractions recorded during labor [13]. This method is similar to the "Snake Ridge" proposed by Carmona and Hwang [14] but uses GVF formulation for external forces, as proposed by Xu and Prince [18]. GVF-Snake method presents a high attraction range, and is thus less sensitive to inaccurate initialization. From a general point of view, this method can be used successfully on various time-frequency representations even those presenting cross-terms like Wigner-Ville representation [19]. In this paper we used this method for the analysis of synthetic signals as well as real EHG.
3. Ridge Reconstruction Methods
Informative parameters on a particular frequency component can be obtained directly in the time-frequency domain. One may however be interested in reconstructing the component in the temporal domain for various reasons. The ridge reconstruction method is dependent on the time-frequency representation (TFR) from which the ridges are extracted. To our knowledge, there have only been proposed reconstruction methods for the Gabor [14] and continuous wavelet [14, 20] TFR.
Continuous wavelet transform (CWT) has been shown to properly represent the frequency content of externally measured human EHG [2, 17]. This time-scale representation has been used for predicting preterm delivery in pregnant women. The continuous wavelet coefficients  of the signal
of the signal  are obtained using the wavelet
are obtained using the wavelet  by the following formula:
by the following formula:

where  and
and  represent the scale and temporal translation parameter, respectively.
represent the scale and temporal translation parameter, respectively.
In this paper, CWT is treated as a TFR since we have chosen scale coefficients  in a way to obtain linear frequency evolution. The square modulus of the CWT is called the scalogram. A complex Morlet wavelet was used for the estimation of the CWT and associated scalogram. We used two reconstruction methods for reconstruction of the ridges extracted from CWT. The first method is referred to as "Marseille method" and the second one as "Carmona's method" [14, 20].
in a way to obtain linear frequency evolution. The square modulus of the CWT is called the scalogram. A complex Morlet wavelet was used for the estimation of the CWT and associated scalogram. We used two reconstruction methods for reconstruction of the ridges extracted from CWT. The first method is referred to as "Marseille method" and the second one as "Carmona's method" [14, 20].
3.1. Marseille Method
This method, proposed by a group in Marseille [20], is the simplest one. Considering a ridge  , the reconstructed analytic signal
, the reconstructed analytic signal  is obtained by:
is obtained by:

where  is the Fourier transform of the wavelet
is the Fourier transform of the wavelet  .
.
3.2. Carmona's Method
This method was proposed by Carmona and Hwang [14]. In this method, it is assumed that the ridge,  , can be parameterized as a continuous function:
, can be parameterized as a continuous function:  ;
;  . Considering the continuous smooth function
. Considering the continuous smooth function  and associated skeleton values
and associated skeleton values  , the reconstructed signal is the function
, the reconstructed signal is the function  which minimizes the cost function
which minimizes the cost function  :
:

with the constraint:

The first term of (3) reinforces the localization of  in the vicinity of
in the vicinity of  while minimizing the global energy of
while minimizing the global energy of  . The second term imposes a slow temporal variation of the amplitude of the reconstructed signal. To explain briefly how this reconstruction method works, one can indicate that the solution of (3) is found by using the Lagrange multipliers with a slight initial modification of the second term, since it is not quadratic in
. The second term imposes a slow temporal variation of the amplitude of the reconstructed signal. To explain briefly how this reconstruction method works, one can indicate that the solution of (3) is found by using the Lagrange multipliers with a slight initial modification of the second term, since it is not quadratic in  . The parameter
. The parameter  has however to be optimized to improve the results of the reconstructed signal. It balances the contribution of the two terms in the global penalty function. The implementation details for (3) can be found in [14].
has however to be optimized to improve the results of the reconstructed signal. It balances the contribution of the two terms in the global penalty function. The implementation details for (3) can be found in [14].
4. Material and Methods
4.1. Signal Description
4.1.1. Synthetic Signals
In order to compare the performances of the Marseille and Carmona's method, we used synthetic signals. No external EHG model is currently available to compare both methods on signals with characteristics close to the real ones. FWH is known to present a fairly strong frequency modulation when compared to FWL. The aspect of this modulation varies strongly from one recording to another as well as between contractions within recordings. It seems to be mainly influenced by the hormonal environment during the recordings, in addition to the variability between individuals. Since the capability of the GVF-snake method to extract the signal time-frequency ridges has already been demonstrated, we fixed the frequency modulation law of the synthetic signals but studied the effect of added noise. We decided to generate signals with a sinusoidal modulation law ranging from 0.02 Hz, at the beginning and the end of the signal, to 0.15 Hz in its middle. We then added zero mean Gaussian white noise. We tested our algorithms by using signal to noise ratio (SNR) of 15, 10, 5 and 1 dB. For each SNR value, we generated 50 synthetic signals.
4.1.2. Real EHG
The measurements were performed by using a 16-channels multipurpose physiological signal recorder (Embla A10). We used reusable Ag/AgCl electrodes. The measurements were performed at the Landspitali University hospital in Iceland, using a protocol approved by the relevant ethical committee (VSN 02-0006-V2).
After obtaining informed consent, the skin was carefully prepared using an abrasive paste and alcoholic solution. After that, the sixteen electrodes were placed on the abdominal wall according to a square matrix ( , inter electrode distance: 2.1 cm). The third electrode column was always put on the uterine median axis and the 10-11th electrode pair on the middle of the uterus (fundus to symphysis). Reference electrodes were placed on each hip of the woman. In order to increase the EHG signal to noise ratio, we considered vertical bipolar signals instead of monopolar ones. The signal sampling rate was 200 Hz. The contractions were then resampled at 20 Hz for more efficient computing. In this initial study, we only considered 5 bipolar channels forming a cross. The central channel was chosen to be the one formed by the 10 and 11th electrodes and thus situated in the classical position for EHG monitoring. The four other channels were the ones above, below, on the right and on the left of the central channel. This gives 5 bursts for a given contraction.
, inter electrode distance: 2.1 cm). The third electrode column was always put on the uterine median axis and the 10-11th electrode pair on the middle of the uterus (fundus to symphysis). Reference electrodes were placed on each hip of the woman. In order to increase the EHG signal to noise ratio, we considered vertical bipolar signals instead of monopolar ones. The signal sampling rate was 200 Hz. The contractions were then resampled at 20 Hz for more efficient computing. In this initial study, we only considered 5 bipolar channels forming a cross. The central channel was chosen to be the one formed by the 10 and 11th electrodes and thus situated in the classical position for EHG monitoring. The four other channels were the ones above, below, on the right and on the left of the central channel. This gives 5 bursts for a given contraction.
We used seven and five recordings on women in pregnancy and labor, respectively. The mean and standard deviations in gestational ages for each group were  and
and  weeks. We randomly selected 15 contractions in each group.
weeks. We randomly selected 15 contractions in each group.
4.2. Evaluation of Reconstruction Performances
In order to evaluate the performances of the two reconstruction methods, we used the normalized percent mean square error (NPMSE) between the reconstructed signals  and the original ones
and the original ones  . This error measure is defined as:
. This error measure is defined as:

For synthetic signal we used only one ridge. For the Carmona's method, we evaluated the effect of the parameter  on the reconstruction error. We tested the set of values
on the reconstruction error. We tested the set of values  . When
. When  , it means that the second term of (3) is not used and is thus not computed.
, it means that the second term of (3) is not used and is thus not computed.
In a previous preliminary study [13], two ridges, supposed to be FWL and FWH, were isolated for the analysis of labor contractions. During the analysis of the reconstruction errors obtained with pregnancy contractions, we observed that two ridges are not always sufficient. A third ridge, called here  for complementary ridge, was searched for when the reconstruction error obtained with FWL and FWH only was above 20% for a given uterine burst. The observation of ridges other than FWL and FWH has been already described in the literature [17].
for complementary ridge, was searched for when the reconstruction error obtained with FWL and FWH only was above 20% for a given uterine burst. The observation of ridges other than FWL and FWH has been already described in the literature [17].
4.3. Labor Prediction
For each contraction, several parameters have been extracted from each ridge. These parameters were compared between each gestational situation, that is, pregnancy and labor.
We used well known parameters already used for the prediction of preterm labor. These parameters for each ridge are:
-
(i)
the minimal and maximal frequencies (Min. F., Max. F.),
-
(ii)
the Mean Frequency (MF),
-
(iii)
the frequency of the maximal energy
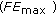 .
.
These parameters were directly computed in the time-frequency domain without ridge reconstruction. In addition, synchronization parameters were computed on the different reconstructed signals obtained for each burst of every selected contraction.
The synchronization between two reconstructed signals where evaluated by using the nonlinear correlation coefficient  . This measure was chosen since it is very simple and it has been proven that almost no linear correlation exists between the temporal bursts in EHG recorded in different positions [21].
. This measure was chosen since it is very simple and it has been proven that almost no linear correlation exists between the temporal bursts in EHG recorded in different positions [21].  is a non parametric nonlinear measure of the relationship between two time series
is a non parametric nonlinear measure of the relationship between two time series  and
and  [22]. In practice, the nonlinear relation between the two time series is approximated by piecewise linear curves. The correlation coefficient
[22]. In practice, the nonlinear relation between the two time series is approximated by piecewise linear curves. The correlation coefficient  is defined as:
is defined as:

where  is the linear piecewise approximation of the nonlinear regression curve. This measure could give information about the directionality of the coupling between the two signals, since
is the linear piecewise approximation of the nonlinear regression curve. This measure could give information about the directionality of the coupling between the two signals, since  might be different of
might be different of  . We chose to use the larger value of the two. We chose to use 15 linear curves in this work. This number was determined empirically.
. We chose to use the larger value of the two. We chose to use 15 linear curves in this work. This number was determined empirically.
To characterize one contraction, we averaged the different ridge parameters values obtained on the 5 available bursts. The comparison of the two groups was done by using non parametric Wilcoxon rank sum test (minimal level of significance of 5%). In order to evaluate the labor prediction capability of one parameter, we used receiver operating characteristic (ROC) curves. ROC curves were compared by mean of the classic Area Under the Curve (AUC) and accuracy (ACC). The AUC was estimated by the trapezoidal integration method. We also used the Matthew's Correlation Coefficient (MCC).
5. Results
5.1. Ridge Reconstruction Method Performances
5.1.1. Synthetic Signals
An example of the deformation process of an initial ridge badly initialized is presented Figure 1. We can see that the ridge quickly converges to the higher energetic positions of the time-frequency plan, despite the relatively low SNR. For each signal realization, the whole process, that is, ridge extraction and reconstruction, was computed. Figure 2 presents the comparison of the reconstruction errors obtained with the Marseille and Carmona's method with  . Carmona's method gave significantly lower reconstruction errors than the Marseille method whatever the SNR. However it has to be noted that the Carmona's method seems less robust. The study of the effect of the second term of (3) used in Carmona's method is presented Table 1. Errors obtained for different
. Carmona's method gave significantly lower reconstruction errors than the Marseille method whatever the SNR. However it has to be noted that the Carmona's method seems less robust. The study of the effect of the second term of (3) used in Carmona's method is presented Table 1. Errors obtained for different  values, for a given SNR, evidenced no significant differences. The computation time of this second term
values, for a given SNR, evidenced no significant differences. The computation time of this second term  increases however drastically the time of the whole reconstruction process (Table 1). Taking into account these results, we chose to use only Carmona's method for real EHG since it seems to give the lowest reconstruction error when compared to the Marseille method. As the value of
increases however drastically the time of the whole reconstruction process (Table 1). Taking into account these results, we chose to use only Carmona's method for real EHG since it seems to give the lowest reconstruction error when compared to the Marseille method. As the value of  did not have any significant influence on the error, we chose to used
did not have any significant influence on the error, we chose to used  .
.
 for different kernel factors
for different kernel factors  and different signal to noise ratios (SNR, dB).
and different signal to noise ratios (SNR, dB).  and
and  represent the computation time without and with the calculation of the second term of (3), respectively.
represent the computation time without and with the calculation of the second term of (3), respectively.5.1.2. Real EHG
Figures 3 and 4 present one example of electrical bursts recorded during pregnancy and labor, respectively. For each signal, the associated scalogram and extracted ridges is also presented on these figures. For the pregnancy burst presented Figure 3, the computation of a complementary ridge ( ) was necessary. This complementary ridge is of lower energy than the ones supposed to be FWL and FWH. It is situated in the higher frequencies of the EHG spectrum. For the labor burst, no complementary ridge was necessary since the reconstruction error obtained with only FWL and FWH was below the 20% threshold, as explained before. This fact was almost observed for all contractions in each respective group. The scalograms of pregnancy bursts were usually more complex than the ones obtained for labor bursts. Figure 5 presents an example of the reconstructed components obtained for a pregnancy burst. We can clearly see that FWL and FWH are the most energetic components. The signal reconstructed by using the sum of FWL and FWH is quite close to the original burst, even if several discrepancies are noticeable. These discrepancies are almost entirely corrected by the addition of the complementary component
) was necessary. This complementary ridge is of lower energy than the ones supposed to be FWL and FWH. It is situated in the higher frequencies of the EHG spectrum. For the labor burst, no complementary ridge was necessary since the reconstruction error obtained with only FWL and FWH was below the 20% threshold, as explained before. This fact was almost observed for all contractions in each respective group. The scalograms of pregnancy bursts were usually more complex than the ones obtained for labor bursts. Figure 5 presents an example of the reconstructed components obtained for a pregnancy burst. We can clearly see that FWL and FWH are the most energetic components. The signal reconstructed by using the sum of FWL and FWH is quite close to the original burst, even if several discrepancies are noticeable. These discrepancies are almost entirely corrected by the addition of the complementary component  . The
. The  seems to only represent details of the original bursts. A summary of the reconstruction errors obtained for each group of contraction is presented Table 2. The reconstruction error obtained with only FWL and FWH is higher for pregnancy contractions than for labor ones. Grouping all contractions gave a reconstruction error of ~19%. The addition of the complementary ridge in both groups diminished the reconstruction error, especially for the pregnancy contractions. The error obtained on average in all contractions is then 16%.
seems to only represent details of the original bursts. A summary of the reconstruction errors obtained for each group of contraction is presented Table 2. The reconstruction error obtained with only FWL and FWH is higher for pregnancy contractions than for labor ones. Grouping all contractions gave a reconstruction error of ~19%. The addition of the complementary ridge in both groups diminished the reconstruction error, especially for the pregnancy contractions. The error obtained on average in all contractions is then 16%.
 (complementary ridge) for pregnancy, labor or all contractions.
(complementary ridge) for pregnancy, labor or all contractions.The ratio of the energy of one component to the energy of the original signal ( CT) is presented Table 3. We can notice that the relative energy of FWL (
CT) is presented Table 3. We can notice that the relative energy of FWL ( ratio FWL) does not vary between pregnancy and labor. No significant difference was found for FWH (
ratio FWL) does not vary between pregnancy and labor. No significant difference was found for FWH ( ratio FWH) despite higher relative energy in labor. The evolution of the relative energy of the complementary component (
ratio FWH) despite higher relative energy in labor. The evolution of the relative energy of the complementary component ( ratio
ratio  ) is significant at
) is significant at  %. It accounts for ~9% of the total energy in pregnancy when compared to ~5% in labor. It has however to be noticed that the number of bursts when a complementary ridge is necessary is lower during labor than during pregnancy. The remaining energy, not accounted for by the two, or three, reconstructed ridges is supposed to be due to the noise present in the signals.
%. It accounts for ~9% of the total energy in pregnancy when compared to ~5% in labor. It has however to be noticed that the number of bursts when a complementary ridge is necessary is lower during labor than during pregnancy. The remaining energy, not accounted for by the two, or three, reconstructed ridges is supposed to be due to the noise present in the signals.
 parameters between pregnancy and labor contractions (
parameters between pregnancy and labor contractions ( and
and  indicate a significant difference of 5% and 1%, respectively, between pregnancy and labor parameters).
indicate a significant difference of 5% and 1%, respectively, between pregnancy and labor parameters).5.2. Labor Prediction
The comparison of classical parameters already used for preterm labor prediction, obtained on each component, between each situation is presented Table 4. We do not notice any significant difference between pregnancy and labor for the parameters obtained with the complementary ridge  . Several parameters obtained from FWL and FWH are however significantly different between pregnancy and labor. These are the frequency of maximal energy
. Several parameters obtained from FWL and FWH are however significantly different between pregnancy and labor. These are the frequency of maximal energy  and mean frequency (MF) of each ridge. The minimal frequency of FWH
and mean frequency (MF) of each ridge. The minimal frequency of FWH  is also significantly different between pregnancy and labor. It might be related to the shift toward the high frequencies of this component, already described in the literature [23].
is also significantly different between pregnancy and labor. It might be related to the shift toward the high frequencies of this component, already described in the literature [23].
 and
and  indicate a significant difference of 5% and 1%, respectively between pregnancy and labor parameters). Min.
indicate a significant difference of 5% and 1%, respectively between pregnancy and labor parameters). Min.  ., Max.
., Max.  ., MF and
., MF and  stand for Minimal Frequency, Maximal Frequency, Mean Frequency and Frequency of the Maximal Energy, respectively. These parameters were computed directly in the time-frequency domain.
stand for Minimal Frequency, Maximal Frequency, Mean Frequency and Frequency of the Maximal Energy, respectively. These parameters were computed directly in the time-frequency domain.The comparison of synchronization measures  is presented Table 5. Since a complementary ridge was not extracted for every burst, we did not compute synchronization measures for this component. We chose instead to compute the measure of the sum of FWH and
is presented Table 5. Since a complementary ridge was not extracted for every burst, we did not compute synchronization measures for this component. We chose instead to compute the measure of the sum of FWH and  , defined as a new composite signal component. Considering FWL and FWH components, only FWL gives a significant difference,
, defined as a new composite signal component. Considering FWL and FWH components, only FWL gives a significant difference,  %, between pregnancy and labor. The synchronization measure obtained on FWL
%, between pregnancy and labor. The synchronization measure obtained on FWL  increases as it is supposed to, if this component is indeed related to a better propagation. When measured either on the raw signal
increases as it is supposed to, if this component is indeed related to a better propagation. When measured either on the raw signal  or on the reconstructed ones
or on the reconstructed ones  and
and  , significant differences are found but only for a significant level of 5%. The use of the reconstructed signals however increases the dynamic range of the parameter
, significant differences are found but only for a significant level of 5%. The use of the reconstructed signals however increases the dynamic range of the parameter  , even if it does not increase the discrimination power of this parameter computed on these signals.
, even if it does not increase the discrimination power of this parameter computed on these signals.
 ) between pregnancy and labor contractions (
) between pregnancy and labor contractions ( and
and  indicate a significant difference of 5 and 1%, respectively between pregnancy and labor parameters).
indicate a significant difference of 5 and 1%, respectively between pregnancy and labor parameters).ROC curves computed for several parameters are presented Figure 6. It can be seen that the curve obtained for  computed on FWH is close to the diagonal and it is therefore not a good parameter for labor prediction (not significant AUC). This confirms the nonsignificant difference obtained with the statistical analysis. The shape of the other significant curves differs for different parameters. It might indicate that the distribution of one parameter according to each class is different to the others. Table 6 summarizes the different characteristics of the obtained ROC curves. The best parameter is surprisingly the mean frequency of FWL. This parameter has never been used in the literature for predicting preterm labor. The worst parameter is the nonlinear correlation computed on FWH, as already stated. The other parameters have almost the same discrimination power when measured with MCC and ACC parameters. The specificity and sensitivity values are however different from one parameter to another.
computed on FWH is close to the diagonal and it is therefore not a good parameter for labor prediction (not significant AUC). This confirms the nonsignificant difference obtained with the statistical analysis. The shape of the other significant curves differs for different parameters. It might indicate that the distribution of one parameter according to each class is different to the others. Table 6 summarizes the different characteristics of the obtained ROC curves. The best parameter is surprisingly the mean frequency of FWL. This parameter has never been used in the literature for predicting preterm labor. The worst parameter is the nonlinear correlation computed on FWH, as already stated. The other parameters have almost the same discrimination power when measured with MCC and ACC parameters. The specificity and sensitivity values are however different from one parameter to another.
 ) and synchronization (
) and synchronization ( ) parameters. AUC, ACC and MCC stand for Area Under the Curve, ACCuracy and Mathews Correlation Coefficient, respectively.
) parameters. AUC, ACC and MCC stand for Area Under the Curve, ACCuracy and Mathews Correlation Coefficient, respectively.6. Discussion
We compared the performances of two ridge reconstruction methods extracted from the continuous wavelet transform of a signal using the GVF-snake method: the Marseille and Carmona's methods. On synthetic signals presenting high frequency modulation, we have shown that Carmona's method gives the lower reconstruction error, whatever the initial signal to noise ratio. Carmona's method however is less robust than the Marseille method. One goal of this study was the optimal choice of the parameter of this method, namely  , which controls the weight of second term of the cost function used in the reconstruction. We have shown that, this second term does not improve the reconstruction. Moreover its computation increases computation time by a factor of more than 50. This second term was necessary for obtaining good performances with non continuous ridges as obtained with the "snake ridge" method originally proposed by Carmona and Hwang [14] but we believe that when using continuous ridges it is unnecessary. The use of non continuous ridges might have advantages in several applications, for example, compression purposes, but is not of interest for EHG signals. The interpolation of several time-frequency points along the ridge,
, which controls the weight of second term of the cost function used in the reconstruction. We have shown that, this second term does not improve the reconstruction. Moreover its computation increases computation time by a factor of more than 50. This second term was necessary for obtaining good performances with non continuous ridges as obtained with the "snake ridge" method originally proposed by Carmona and Hwang [14] but we believe that when using continuous ridges it is unnecessary. The use of non continuous ridges might have advantages in several applications, for example, compression purposes, but is not of interest for EHG signals. The interpolation of several time-frequency points along the ridge,  , by a continuous function,
, by a continuous function,  , imposes additional constraints on the possible reconstructed signal
, imposes additional constraints on the possible reconstructed signal  . These constraints are controlled by the value of
. These constraints are controlled by the value of  . The continuous estimation of the ridge
. The continuous estimation of the ridge  by the GVF-snake method reduces the need to impose these constraints. They may however play a role in the performances of the method in the presence of low SNR. Our results show that for the SNR range used in this study, the improvements obtained by applying these constraints are not significant.
by the GVF-snake method reduces the need to impose these constraints. They may however play a role in the performances of the method in the presence of low SNR. Our results show that for the SNR range used in this study, the improvements obtained by applying these constraints are not significant.
The small reconstruction errors obtained with Carmona's method seems to indicate that the two ridges, supposed to be FWL and FWH, are enough to account for almost 80% of the total energy of EHG bursts. The method seems generally to be well suited for the characterization of contraction for pregnancy monitoring. Sometimes, especially for bursts recorded during pregnancy, a third ridge was necessary in order to reduce the reconstruction error below 20%. The physiological interpretation or origin of this complementary ridge is not yet clear and remains an open question. In regards to the results obtained, no significant differences in the energy ratio of FWL and FWH were observed between the signals obtained in pregnancy and labor. This may indicate that this third component is simply due to a lower signal to noise ratio for signals recorded during pregnancy.
As in [2, 14], we use the extracted/reconstructed ridges of EHG bursts for the prediction of human labor. We used both classical and new parameters. Several studies, have used parameters like mean frequency or frequency of maximal energy for the prediction of preterm labor with some success [2, 3, 5, 6, 17]. Our results also show that these parameters present significant changes between pregnancy and labor as attested by statistical tests as well as by ROC curves analysis.
The parameters were all obtained on the scalogram of the EHG bursts. This time-frequency representation is well known to be blurred by construction and also for its extreme redundancy. The use of more recent time-frequency estimators presenting better concentration around the signal frequency components may further increase the quality of the extraction of the time-frequency parameters. These methods include but are not limited to the methods discussed in [23–27]. A comparison of these new estimators and the scalogram, for the application to the EHG, is outside the scope of this paper but may be an interesting topic for a study in itself.
The main contribution of our study resides in the use of synchronization parameters for the prediction of labor. The uterus is supposed to synchronize as labor approaches, in order to produce forceful contractions that are able to efficiently push the baby into the world. In this paper, we used the nonlinear correlation coefficient as a synchronization measure. The highest synchronization changes are observed for the FWL component. This tends to confirm the hypothesis concerning the link of this frequency component with the propagation of the contractions in the uterus. The synchronization measures obtained with FWH, often supposed to be linked with the excitability of the uterus, does not significantly change between pregnancy and labor. High synchronization values were however observed. A possible bias in the synchronization analysis might explain these high values [8]. Considering parameters evolving significantly from pregnancy to labor, we have shown that they do not all have the same prediction capability. Important differences in specificity and sensitivity may indicate that a combination of these parameters may increase the overall labor prediction performances. Using several parameters at the same time can however not be done with ROC curves. More recent and sophisticated methods like Neural Networks or Support Vector Machine methods are required to fully exploit the potential of the complementary information provided by our approach. Work on this is planned in our group by using multi parametric decision tool in order to combine several parameters at the same time for further increasing the performances of the labor prediction.
An interesting perspective study is the evaluation of different synchronization measures for labor prediction purposes, as we have only used the nonlinear correlation coefficient in this work. The different measures proposed in the literature are sensitive to a particular nature of the coupling between two signals [22], for example, amplitude, phase. The detailed nature of the coupling between EHG bursts on two sites on the abdomen has not yet been identified. The use of the directionality information available with  may also be important for better prediction of labor and later on, of preterm labor.
may also be important for better prediction of labor and later on, of preterm labor.
7. Conclusion
In this paper we compared the performances of two ridge reconstruction methods namely Carmona's and Marseille methods. We showed on synthetic signals as well as on real uterine electromyograms or electrohysterograms (EHG), that Carmona's method allows us to obtained significant lower reconstruction errors than the Marseille method. The possibility of reconstructing the EHG frequency components independently allowed us to propose new parameters for labor prediction based on the synchronization of the uterus. For a first time, we used the nonlinear correlation coefficient to measure the coupling that might exist between two EHG bursts. The results seem to indicate that the classical time-frequency parameters and the new synchronization ones are complementary and may thus increase the prediction of labor.
References
Marque CK, Terrien J, Rihana S, Germain G: Preterm labour detection by use of a biophysical marker: the uterine electrical activity. BMC Pregnancy and Childbirth 2007., 7(1, supplement):
Leman H, Marque C, Gondry J: Use of the electrohysterogram signal for characterization of contractions during pregnancy. IEEE Transactions on Biomedical Engineering 1999, 46(10):1222-1229. 10.1109/10.790499
Maner WL, Garfield RE, Maul H, Olson G, Saade G: Predicting term and preterm delivery with transabdominal uterine electromyography. Obstetrics and Gynecology 2003, 101(6):1254-1260. 10.1016/S0029-7844(03)00341-7
Devedeux D, Marque C, Mansour S, Germain G, Duchene J: Uterine electromyography: a critical review. American Journal of Obstetrics and Gynecology 1993, 169(6):1636-1653.
Buhimschi C, Boyle MB, Garfield RE: Electrical activity of the human uterus during pregnancy as recorded from the abdominal surface. Obstetrics and Gynecology 1997, 90(1):102-111. 10.1016/S0029-7844(97)83837-9
Maner WL, Garfield RE: Identification of human term and preterm labor using artificial neural networks on uterine electromyography data. Annals of Biomedical Engineering 2007, 35(3):465-473. 10.1007/s10439-006-9248-8
Euliano TY, Marossero D, Nguyen MT, Euliano NR, Principe J, Edwards RK: Spatiotemporal electrohysterography patterns in normal and arrested labor. American Journal of Obstetrics and Gynecology 2009, 200(1): 54.e1-54.e7. 10.1016/j.ajog.2008.09.008
Terrien J, Marque C, Germain G, Karlsson B: Sources of bias in synchronization measures and how to minimize their effects on the estimation of synchronicity: application to the uterine electromyogram. In Recent Advances in Biomedical Engineering. Edited by: Naik GR. In-Tech, Vienne, Autriche; 2009:73-99.
Terrien J, Hassan M, Germain G, Marque C, Karlsson B: Nonlinearity testing in the case of non Gaussian surrogates, applied to improving analysis of synchronicity in uterine contraction. Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society: Engineering the Future of Biomedicine (EMBC '09), 2009 3477-3480.
Balducci J, Risek B, Gilula NB, Hand A, Egan JFX, Vintzileos AM: Gap junction formation in human myometrium: a key to preterm labor? American Journal of Obstetrics and Gynecology 1993, 168(5):1609-1615.
Garfield RE, Hayashi RH: Appearance of gap junctions in the myometrium of women during labor. American Journal of Obstetrics and Gynecology 1981, 140(3):254-260.
Terrien J, Marque C, Germain G: Ridge extraction from the time-frequency representation (TFR) of signals based on an image processing approach: application to the analysis of uterine electromyogram AR TFR. IEEE Transactions on Biomedical Engineering 2008, 55(5):1496-1503.
Terrien J, Marque C, Karlsson B: Spectral characterization of human EHG frequency components based on the extraction and reconstruction of the ridges in the scalogram. Proceedings of the 29th Annual International Conference of the IEEE-EMBS, Engineering in Medicine and Biology Society (EMBC '07), August 2007, Lyon, France 1872-1875.
Carmona RA, Hwang WL: Characterization of signals by the ridges of their wavelet transforms. IEEE Transactions on Signal Processing 1997, 45(10):2586-2590. 10.1109/78.640725
Michel O, Flandrin P, Hero AO III: Automatic extraction of time-frequency skeletons with minimal spanning trees. Proceedings IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '00), 2000, Istambul, Turkey 1: 89-92.
Duchêne J, Devedeux D, Mansour S, Marque C: Analyzing uterine EMG: tracking instantaneous burst frequency. IEEE Engineering in Medicine and Biology Magazine 1995, 14(2):125-132. 10.1109/51.376749
Leman H, Marque C: Ridge extraction from the scalogram of the uterine electromyogram. Proceedings of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis (TFTS '98), October 1998, Pittsburgh, Pa, USA 245-248.
Xu C, Prince JL: Generalized gradient vector flow external forces for active contours. Signal Processing 1998, 71(2):131-139. 10.1016/S0165-1684(98)00140-6
Terrien J, Marque C, Germain G: Utilisation des contours actifs ou "snake" pour l'extraction des arêtes de représentations temps-fréquences: application à l'analyse des contractions utérines. In 20ème Colloque GRETSI sur le traitement du signal et des images, 2005, Belgique, France. Louvain-la-Neuve;
Tchamitchian P, Torrésani B: Ridge and skeleton extraction from wavelet transform. In Wavelets and Their Applications. Edited by: Ruskai MB. Jones & Bartlett, Boston, Mass, USA; 1991.
Mansour S, Devedeux D, Germain G, Marque C, Duchêne J: Uterine EMG spectral analysis and relationship to mechanical activity in pregnant monkeys. Medical and Biological Engineering and Computing 1996, 34(2):115-121. 10.1007/BF02520015
Pereda E, Quiroga RQ, Bhattacharya J: Nonlinear multivariate analysis of neurophysiological signals. Progress in Neurobiology 2005, 77(1-2):1-37. 10.1016/j.pneurobio.2005.10.003
Shafi I, Ahmad J, Shah SI, Kashif FM: Computing deblurred time-frequency distributions using artificial neural networks. Circuits, Systems, and Signal Processing 2008, 27(3):277-294. 10.1007/s00034-008-9027-x
Orović I, Stanković S: A class of highly concentrated time-frequency distributions based on the ambiguity domain representation and complex-lag moment. EURASIP Journal on Advances in Signal Processing 2009, 2009:-9.
Shafi I, Ahmad J, Shah SI, Kashif FM: Evolutionary time-frequency distributions using Bayesian regularised neural network model. IET Signal Processing 2007, 1(2):97-106. 10.1049/iet-spr:20060311
Jachan M, Matz G, Hlawatsch F: Time-frequency ARMA models and parameter estimators for underspread nonstationary random processes. IEEE Transactions on Signal Processing 2007, 55(9):4366-4381.
Shafi I, Ahmad J, Shah SI, Kashif FM: Techniques to obtain good resolution and concentrated time-frequency distributions: a review. EURASIP Journal on Advances in Signal Processing 2009, 2009:-43.
Acknowledgments
This paper was supported by the Icelandic center of research, RANNIS. The authors want to thank Ásgeir Alexanderson for recording the human EHG as well as all subjects who agreed to participate in this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Terrien, J., Steingrimsdottir, T., Marque, C. et al. Synchronization between EMG at Different Uterine Locations Investigated Using Time-Frequency Ridge Reconstruction: Comparison of Pregnancy and Labor Contractions. EURASIP J. Adv. Signal Process. 2010, 242493 (2010). https://doi.org/10.1155/2010/242493
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/242493
 .
.
 , where x represents the number of iterations.
, where x represents the number of iterations.  represents the initial snake and
represents the initial snake and  the final extracted ridge.
the final extracted ridge.



