- Research Article
- Open access
- Published:
Improving Density Estimation by Incorporating Spatial Information
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 265631 (2010)
Abstract
Given discrete event data, we wish to produce a probability density that can model the relative probability of events occurring in a spatial region. Common methods of density estimation, such as Kernel Density Estimation, do not incorporate geographical information. Using these methods could result in nonnegligible portions of the support of the density in unrealistic geographic locations. For example, crime density estimation models that do not take geographic information into account may predict events in unlikely places such as oceans, mountains, and so forth. We propose a set of Maximum Penalized Likelihood Estimation methods based on Total Variation and  Sobolev norm regularizers in conjunction with a priori high resolution spatial data to obtain more geographically accurate density estimates. We apply this method to a residential burglary data set of the San Fernando Valley using geographic features obtained from satellite images of the region and housing density information.
Sobolev norm regularizers in conjunction with a priori high resolution spatial data to obtain more geographically accurate density estimates. We apply this method to a residential burglary data set of the San Fernando Valley using geographic features obtained from satellite images of the region and housing density information.
1. Introduction
High resolution and hyperspectral satellite images, city and county boundary maps, census data, and other types of geographical data provide much information about a given region. It is desirable to integrate this knowledge into models defining geographically dependent data. Given spatial event data, we will be constructing a probability density that estimates the probability that an event will occur in a region. Often, it is unreasonable for events to occur in certain regions, and we would like our model to reflect this restriction. For example, residential burglaries and other types of crimes are unlikely to occur in oceans, mountains, and other regions. Such areas can be determined using aerial images or other external spatial data, and we denote these improbable locations as the invalid region. Ideally, the support of our density should be contained in the valid region.
Geographic profiling, a related topic, is a technique used to create a probability density from a set of crimes by a single individual to predict where the individual is likely to live or work [1]. Some law enforcement agencies currently use software that makes predictions in unrealistic geographic locations. Methods that incorporate geographic information have recently been proposed and are an active area of research [2, 3].
A common method for creating a probability density is to use Kernel Density Estimation [4, 5], which approximates the true density by a sum of kernel functions. A popular choice for the kernel is the Gaussian distribution which is smooth, spatially symmetric and has noncompact support. Other probability density estimation methods include the taut string, logspline, and the Total Variation Maximum Penalized Likelihood Estimation models [6–10]. However, none of these methods utilize information from external spatial data. Consequently, the density estimate typically has some nonzero probability of events occurring in the invalid region. Figure 1 demonstrates these problems with the current methods and how the methods we will propose in this paper resolve them. Located in the middle of the image are two disks where events cannot occur, depicted in Figure 1(a). We selected randomly from the region outside the disks using a predefined probabilistic density, that is, provided in Figure 1(b). The 4,000 events chosen are shown in Figure 1(c). With a variance of  , we see in Figure 1(d) that the Kernel Density Estimation predicts that events may occur in our invalid region.
, we see in Figure 1(d) that the Kernel Density Estimation predicts that events may occur in our invalid region.
This is a motivating example that demonstrates the problem with existing methods and how our methods will improve density estimates. (a) and (b) give the valid region to be considered and the true density for the example. Figure (c) gives the 4000 events sampled from the true density. (d) and (e) show two of the current methods used. (f), (g), and (h) show how our methods will produce better estimates. The color scale represents the relative probability of an event occurring in a given pixel. The images are 80 pixels by 80 pixels. (a) Valid region, (b) True density, (c) 4,000 events, (d) Kernel density estimate, (e) TV MPLE, (f) Our modified TV MPLE method, (g) Our weighted H1 MPLE method (h) Our weighted TV MPLE method.
In this paper we propose a novel set of models that restrict the support of the density estimate to the valid region and ensure realistic behavior. The models use Maximum Penalized Likelihood Estimation [11, 12], which is a variational approach. The density estimate is calculated as the minimizer of some predefined energy functional. The novelty of our approach is in the way we define the energy functional with explicit dependence on the valid region such that the density estimate obeys our assumptions of its support. The results from our methods for this simple example are illustrated in Figures 1(f), 1(g), and 1(h).
The paper is structured in the following way. In Section 2 Maximum Penalized Likelihood Methods are introduced. In Sections 3 and 4 we present our set of models which we name the Modified Total Variation MPLE model and the Weighted Sobolev MPLE model, respectively. In Section 5 we discuss the implementation and numerical schemes that we use to solve for the solutions of the models. We provide examples for validation of the models and an example with actual residential burglary data in Section 6. In this Section, we also compare our results to the Kernel Density Estimation model and other Total Variation MPLE methods. Finally, we discuss our conclusions and future work in Section 7.
Sobolev MPLE model, respectively. In Section 5 we discuss the implementation and numerical schemes that we use to solve for the solutions of the models. We provide examples for validation of the models and an example with actual residential burglary data in Section 6. In this Section, we also compare our results to the Kernel Density Estimation model and other Total Variation MPLE methods. Finally, we discuss our conclusions and future work in Section 7.
2. Maximum Penalized Likelihood Estimation
Assuming that  is the desired probability density for
is the desired probability density for  and the known location of events occur at
and the known location of events occur at  , then Maximum Penalized Likelihood Estimation (MPLE) models are given by
, then Maximum Penalized Likelihood Estimation (MPLE) models are given by

Here,  is a penalty functional, which is generally designed to produce a smooth density map. The parameter
is a penalty functional, which is generally designed to produce a smooth density map. The parameter  determines how strongly weighted the maximum likelihood term is, compared to the penalty functional:
determines how strongly weighted the maximum likelihood term is, compared to the penalty functional:
A range of penalty functionals has been proposed, including  [11, 12] and
[11, 12] and 
 [4, 11]. More recently, variants of the Total Variation (TV) functional [13],
[4, 11]. More recently, variants of the Total Variation (TV) functional [13],  , have been proposed for MPLE [8–10]. These methods do not explicitly incorporate the information that can be obtained from the external spatial data, although some note the need to allow for various domains. Even though the TV functional will maintain sharp gradients, the boundaries of the constant regions do not necessarily agree with the boundaries within the image. This method also performs poorly when the data is too sparse, as the density is smoothed to have equal probability almost everywhere. Figure 1(e) demonstrates this, in addition to how this method predicts events in the invalid region with nonnegligible estimates.
, have been proposed for MPLE [8–10]. These methods do not explicitly incorporate the information that can be obtained from the external spatial data, although some note the need to allow for various domains. Even though the TV functional will maintain sharp gradients, the boundaries of the constant regions do not necessarily agree with the boundaries within the image. This method also performs poorly when the data is too sparse, as the density is smoothed to have equal probability almost everywhere. Figure 1(e) demonstrates this, in addition to how this method predicts events in the invalid region with nonnegligible estimates.
The methods we propose use a penalty functional that depends on the valid region determined from the geographical images or other external spatial data. Figure 1 demonstrates how these models will improve on the current methods.
3. The Modified Total Variation MPLE Model
The first model we propose is an extension of the Maximum Penalized Likelihood Estimation method given by Mohler et al. [10]

Once we have determined a valid region, we wish to align the level curves of the density function  with the boundary of the valid region. The Total Variation functional is well known to allow discontinuities in its minimizing solution [13]. By aligning the level curves of the density function with the boundary, we encourage a discontinuity to occur there to keep the density from smoothing into the invalid region.
with the boundary of the valid region. The Total Variation functional is well known to allow discontinuities in its minimizing solution [13]. By aligning the level curves of the density function with the boundary, we encourage a discontinuity to occur there to keep the density from smoothing into the invalid region.
Since  gives the unit normal vectors to the level curves of
gives the unit normal vectors to the level curves of  , we would like
, we would like

where  is the characteristic function of the valid region
is the characteristic function of the valid region  . The region
. The region  is obtained from external spatial data, such as aerial images. To avoid division by zero, we use
is obtained from external spatial data, such as aerial images. To avoid division by zero, we use  , where
, where  . To align the density function and the boundary one would want to minimize
. To align the density function and the boundary one would want to minimize  . Integrating this and applying integration by parts, we obtain the term
. Integrating this and applying integration by parts, we obtain the term  . We propose the following Modified Total Variation penalty functional, where we adopt the more general form of the above functional:
. We propose the following Modified Total Variation penalty functional, where we adopt the more general form of the above functional:

The parameter  allows us to vary the strength of the alignment term. Two pan-sharpening methods,
allows us to vary the strength of the alignment term. Two pan-sharpening methods,  and Variational Wavelet Pan-sharpening [14, 15], both include a similar term in their energy functional to align the level curves of the optimal image with the level curves of the high resolution pan-chromatic image.
and Variational Wavelet Pan-sharpening [14, 15], both include a similar term in their energy functional to align the level curves of the optimal image with the level curves of the high resolution pan-chromatic image.
4. The Weighted 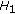 Sobolev MPLE Model
Sobolev MPLE Model
A Maximum Penalized Likelihood Estimation method with penalty functional  , the
, the  Sobolev norm, gives results equivalent to those obtained using Kernel Density Estimation [11]. We enforce the
Sobolev norm, gives results equivalent to those obtained using Kernel Density Estimation [11]. We enforce the  regularizer term away from the boundary of the invalid region. This results in the model
regularizer term away from the boundary of the invalid region. This results in the model

This new term is essentially the smoothness term from the Mumford-Shah model [16]. We approximate the  term by introducing the Ambrosio-Tortorelli approximating function
term by introducing the Ambrosio-Tortorelli approximating function  [17], where
[17], where  in the sense of distributions. More precisely, we use a continuous function which has the property
in the sense of distributions. More precisely, we use a continuous function which has the property

Thus, the minimization problem becomes

The weighting away from the edges is used to control the diffusion into the invalid region. This method of weighting away from the edges can also be used with the Total Variation functional in our first model, and we will refer to this as our Weighted TV MPLE model.
5. Implementation
5.1. The Constraints
In the implementation for the Modified Total Variation MPLE method and Weighted  MPLE method, we must enforce the constraints
MPLE method, we must enforce the constraints  and
and  to ensure that
to ensure that  is a probability density estimate. The
is a probability density estimate. The  constraint will be satisfied in our numerical solution by solving quadratic equations that have at least one nonnegative root.
constraint will be satisfied in our numerical solution by solving quadratic equations that have at least one nonnegative root.
We enforce the second constraint by first adding it to the energy functional as an  penalty term. For the
penalty term. For the  method, this change results in the new minimization problem
method, this change results in the new minimization problem

where we have denoted  as the solution of the
as the solution of the  model. The constraint is then enforced by applying Bregman iteration [18]. Using this method, we formulate our problem as
model. The constraint is then enforced by applying Bregman iteration [18]. Using this method, we formulate our problem as

where  is introduced as the Bregman variable of the sum to unity constraint. We solve this problem using alternating minimization, updating the
is introduced as the Bregman variable of the sum to unity constraint. We solve this problem using alternating minimization, updating the  and the
and the  iterates as
iterates as

with  Similarly for the modified TV method, we solve the alternating minimization problem
Similarly for the modified TV method, we solve the alternating minimization problem

with 
5.2. Weighted 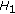 MPLE Implementation
MPLE Implementation
For the Weighted  MPLE model, the Euler-Lagrange equation for the
MPLE model, the Euler-Lagrange equation for the  minimization is given by
minimization is given by

We solve this using a Gauss-Seidel method with central differences for the  and
and  . Once we have discretized the partial differential equation, solving this equation simplifies solving the quadratic
. Once we have discretized the partial differential equation, solving this equation simplifies solving the quadratic

for the positive root, where

and where  is the given number of sampled events that occurred at the location
is the given number of sampled events that occurred at the location  . We chose our parameters
. We chose our parameters  and
and  so that the Gauss-Seidel solver will converge. In particular, we have
so that the Gauss-Seidel solver will converge. In particular, we have  and
and  , where the image is
, where the image is  .
.
5.3. Modified TV MPLE Implementation
There are many approaches for handling the minimization of the Total Variation penalty functional. A fast and simple method for doing this is to use the Split Bregman technique (see [10, 19] for an in depth discussion, see also [20]). In this approach, we substitute the variable  for
for  in the TV norm and then enforce the equality
in the TV norm and then enforce the equality  using Bregman iteration. To apply Bregman iteration, we introduce the variable
using Bregman iteration. To apply Bregman iteration, we introduce the variable  as the Bregman vector of the
as the Bregman vector of the  constraint. This results in a minimization problem in which we minimize both
constraint. This results in a minimization problem in which we minimize both  and
and  .
.
Beginning the iteration with  , the minimization is written as
, the minimization is written as

Alternating the minimization of  and
and  , we obtain our final formulation for the TV model as
, we obtain our final formulation for the TV model as

The shrink function is given by

Solving for  and
and  we use forward difference discretizations, namely
we use forward difference discretizations, namely

The Euler-Lagrange equations for the variable  is
is

Discretizing this simplifies solving for the positive root of

where

We solved for  with a Gauss-Seidel solver. Heuristically, we found that using the relationships
with a Gauss-Seidel solver. Heuristically, we found that using the relationships  and
and  were sufficient for the solver to converge and provide good results. We also set
were sufficient for the solver to converge and provide good results. We also set  to have values between
to have values between  and
and  . The parameter
. The parameter  is the last remaining free paramter. This parameter can be chosen using V-cross validation or other techniques, such as the sparsity
is the last remaining free paramter. This parameter can be chosen using V-cross validation or other techniques, such as the sparsity  information criterion [8].
information criterion [8].
6. Results
In this Section, we demonstrate the strengths of our models by providing several examples. We first show how our methods compare to existing methods for a dense data set. We then show that our methods perform well for sparse data sets. Next, we explore an example with an aerial image and randomly selected events to show how these methods could be applied to geographic event data. Finally, we calculate probability density estimates for residential burglaries using our models.
6.1. Model Validation Example
To validate the use of our methods, we took a predefined probability map with sharp gradients that is shown in Figure 2(a). The chosen valid region and the 8,000 selected events are displayed in Figures 2(b) and 2(c), respectively. We performed density estimates with the Gaussian Kernel Density Estimate and the Total Variation MPLE method. The variance used for the Kernel Density Estimation is  . The results are provided in Figures 2(d) and 2(e). The density estimates obtained from our Modified TV MPLE method and Weighted
. The results are provided in Figures 2(d) and 2(e). The density estimates obtained from our Modified TV MPLE method and Weighted  MPLE method are shown in Figures 2(f) and 2(g), respectively. We also included our Weighted TV MPLE in Figure 2(h).
MPLE method are shown in Figures 2(f) and 2(g), respectively. We also included our Weighted TV MPLE in Figure 2(h).
This is a model-validating example with dense data set of 8000 events. The piecewise-constant true density is given in (a), and the valid region is provided in (b). The sampled events are shown in (c). (d) and (e) show the two current density estimation methods, Kernel Density Estimation and TV MPLE. (f), (g), and (h) show the density estimates from our methods. The color scale represents the relative probability of an event occurring in a given pixel. The images are 80 pixels by 80 pixels. (a) True density, (b) Valid region, (c) 8,000 events, (d) Kernel density estimation, (e) TV MPLE method, (f) Our modified TV MPLE method, (g) Our weighted H1 MPLE methodOur weighted TV MPLE method
Our methods maintain the boundary of the invalid region and appear close to the true solution. In addition, they keep the sharp gradient in the density estimate. The  errors for these methods are located in Table 1.
errors for these methods are located in Table 1.
 error comparison of the five methods shown in Figure 2. Our proposed methods performed better than both the Kernel Density Estimation method and the TV MPLE method.
error comparison of the five methods shown in Figure 2. Our proposed methods performed better than both the Kernel Density Estimation method and the TV MPLE method.6.2. Sparse Data Example
Crimes and other types of events may be quite sparse in a given geographical region. Consequently, it becomes difficult to determine the probability that an event will occur in the area. It is challenging for density estimation methods that do not incorporate the spatial information to distinguish between invalid regions and areas that have not had any crimes but are still likely to have events. Using the same predefined probability density from Section 1 in Figure 1(b), we demonstrate how our methods maintain these invalid regions for sparse data. The 40 events selected are shown in Figure 3(b). The density estimates for current methods and our methods are given in Figure 3. We used a variance  for the Gaussian Kernel Density Estimate.
for the Gaussian Kernel Density Estimate.
This is a sparse example with 40 events. The true density is given in (a), and it is the same density from the example in the introduction. The sampled events are shown in (b). (c) and (d) show the two current density estimation methods, Kernel Density Estimation and TV MPLE. (e), (f), and (g) show the density estimates from our methods. The color scale represents the relative probability of an event occurring in a given pixel. The images are 80 pixels by 80 pixels. (a) True density, (b) 40 Events, (c) Kernel density estimation, (d) TV MPLE method, (e) Our modified TV MPLE method, (f) Our weighted H1 MPLE method, (g) Our weighted TV MPLE method.
For this sparse problem, our Weighted  MPLE and Modified TV MPLE methods maintain the boundary of the invalid region and appear close to the true solution. Table 2 contains the
MPLE and Modified TV MPLE methods maintain the boundary of the invalid region and appear close to the true solution. Table 2 contains the  errors for both this example of 40 events and the example of 4,000 events from the introduction. Notice that our Modified TV and Weighted
errors for both this example of 40 events and the example of 4,000 events from the introduction. Notice that our Modified TV and Weighted  MPLE methods performed the best for both examples. The Weighted
MPLE methods performed the best for both examples. The Weighted  MPLE was exceptionally better for the sparse data set. The Weighted TV MPLE method does not perform as well for sparse data sets and fails to keep the boundary of the valid region. Since the rest of the examples contains sparse data sets, we will omit the Weighted TV MPLE method from the remaining sections.
MPLE was exceptionally better for the sparse data set. The Weighted TV MPLE method does not perform as well for sparse data sets and fails to keep the boundary of the valid region. Since the rest of the examples contains sparse data sets, we will omit the Weighted TV MPLE method from the remaining sections.
 error comparison of the five methods for both the introductory example shown in Figure 1 and the sparse example shown in Figure 3. Our proposed methods performed better than both the Kernel Density Estimation method and the TV MPLE method.
error comparison of the five methods for both the introductory example shown in Figure 1 and the sparse example shown in Figure 3. Our proposed methods performed better than both the Kernel Density Estimation method and the TV MPLE method.6.3. Orange County Coastline Example
To test the models with external spatial data, we obtained from Google Earth a region of the Orange County coastline with clear invalid regions (see Figure 4(a)). For the purposes of this example, it was determined to be impossible for events to occur in the ocean, rivers, or large parks located in the middle of the region. One may use various segmentation methods for selecting the valid region. For this example, we only have data from the true color aerial image, not multispectral data. To obtain the valid and invalid regions, we removed the "texture" (i.e., fine detailed features) using a Total Variation-based denoising algorithm [13]. The resulting image, shown in Figure 4(b), still contains detailed regions obtained from large features, such as large buildings. We wish to remove these and maintain prominent regional boundaries. Therefore, we smooth away from regions of large discontinuities. This is shown in Figure 4(c). Since oceans, rivers, parks, and other such areas have generally lower intensity values than other regions, we threshold to find the boundary between the valid and invalid regions. The final valid region is displayed in Figure 5(a).
This shows how we obtained our valid region for the Orange County Coastline example. Figure (a) is the initial aerial image of the region to be considered. The region of interest is about 15.2 km by 10 km. Figure (b) is the denoised version of the initial image. We took this denoised image and smoothed away from regions of large discontinuities to obtain figure (c)., (a) Google earth image of orange county coastline, (b)Orange county coastline denoised image, (c)Orange county coastline smoothed image
After thresholding the intensity values of Figure 4(c), we obtain the valid region for the Orange County Coastline. This valid region is shown in (a). We then constructed a probability density shown in figure (b). The color scale represents the relative probability of an event occurring per square kilometer. (a) Orange county coastline valid region, (b) OC coastline density map.
From the valid region, we constructed a toy density map to represent the probability density for the example and to generate data. It is depicted in Figure 5(b). Regions with colors farther to the right on the color scale are more likely to have events. Sampling from this constructed density, we took distinct data sets of 200, 2,000, and 20,000 selected events given in Figure 6. For each set of events, we included three probability density estimations for comparison. We first give the Gaussian Kernel Density Estimate followed by our Modified Total Variation MPLE model and our Weighted  MPLE model. We provide all images together to allow for visual comparisons of the methods.
MPLE model. We provide all images together to allow for visual comparisons of the methods.
From the probability density in Figure 5, we sampled 200, 2,000, and 20,000 events. These events are given in (a), (b), and (c), respectively. (a) OC coastline 200 events, (b) OC coastline 2,000 events, (c) OC coastline 20,000 events
Summing up Gaussian distributions gives a smooth density estimate. Figure 7 contains the density estimates obtained using the Kernel Density Estimation model. The standard deviations  of the Gaussians are given with each image. In all of these images, a nonzero density is estimated in the invalid region.
of the Gaussians are given with each image. In all of these images, a nonzero density is estimated in the invalid region.
These images are the Gaussian Kernel Density estimates for 200, 2,000, and 20,000 sampled events of the Orange County Coastline example. The color scale for these images is located in Figure 5. (a) OC coastline kernel density estimate 200 samples with σ = 35, (b) OC coastline kernel density estimate 2,000 samples with σ = 18, (c) OC coastline kernel density estimate 20,000 samples with σ = 6.25.
Taking the same set of events as the Kernel density estimation, the images in Figure 8 were obtained using our first model, the Modified Total Variation MPLE method with the boundary edge aligning term. The parameter for  must be sufficiently large in the TV method in order to prevent the diffusion of the density into the invalid region. In doing so, the boundary of the valid region may attain density values too large in comparison to the rest of the image when the size of the image is very large. To remedy this, we may take the resulting image from the algorithm and set the boundary of the valid region to zero and rescale the image to have a sum of one. The invalid region in this case sometimes has a very small nonzero estimate. For visualization purposes we have set this to zero. However, we note that the method has the strength that density does not diffuse through small Sections of the invalid region back into the valid region on the opposite side. Events on one side of an object, such as a lake or river, should not necessarily predict events on the other side.
must be sufficiently large in the TV method in order to prevent the diffusion of the density into the invalid region. In doing so, the boundary of the valid region may attain density values too large in comparison to the rest of the image when the size of the image is very large. To remedy this, we may take the resulting image from the algorithm and set the boundary of the valid region to zero and rescale the image to have a sum of one. The invalid region in this case sometimes has a very small nonzero estimate. For visualization purposes we have set this to zero. However, we note that the method has the strength that density does not diffuse through small Sections of the invalid region back into the valid region on the opposite side. Events on one side of an object, such as a lake or river, should not necessarily predict events on the other side.
These images are the Modified TV MPLE estimates for 200, 2,000, and 20,000 sampled events of the Orange County Coastline example. The color scale for these images is located in Figure 5. (a) OC coastline modified TV MPLE 200 samples, (b) OC coastline modified TV MPLE 2,000 samples, (c) OC coastline modified TV MPLE 20,000 samples
The next set of images in Figure 9 estimate the density using the same sets of event data but with our Weighted  MPLE model. Notice the difference for the invalid regions with our models and the Kernel Density Estimation model. This method does very well for the sparse data sets of 200 and 2,000 events.
MPLE model. Notice the difference for the invalid regions with our models and the Kernel Density Estimation model. This method does very well for the sparse data sets of 200 and 2,000 events.
These images are the Weighted H1 MPLE estimates for 200, 2,000, and 20,000 sampled events of the Orange County Coastline example. The color scale for these images are located in Figure 5. (a) OC coastline weighted H1 MPL estimate 200 samples, (b)OC coastline weighted H1 MPL estimate 2,000 samples, (c) OC coastline weighted H1 MPL estimate 20,000 samples
6.3.1. Model Comparisons
The density estimates obtained from using our methods have a clear improvement in maintaining the boundary of the valid region. To determine how our models did in comparison to one another and to the Kernel Density Estimate, we calculated the  errors located in Table 3. Our models consistently outperform the Kernel Density Estimation model. The Weighted
errors located in Table 3. Our models consistently outperform the Kernel Density Estimation model. The Weighted  MPLE method performs the best for the 2,000 and 20,000 events and visually appears closer to the true solution for the 200 events than the other methods. Qualitatively, we have noticed that with sparse data, the TV penalty functional gives results which are near constant. Thus, it gives a good
MPLE method performs the best for the 2,000 and 20,000 events and visually appears closer to the true solution for the 200 events than the other methods. Qualitatively, we have noticed that with sparse data, the TV penalty functional gives results which are near constant. Thus, it gives a good  error for the Orange County Coastline example, which has piecewise-constant true density, but gives a worse result for the sparse data example of Figure 3, where the true density has a nonzero gradient. Even though the Modified TV MPLE method has a lower
error for the Orange County Coastline example, which has piecewise-constant true density, but gives a worse result for the sparse data example of Figure 3, where the true density has a nonzero gradient. Even though the Modified TV MPLE method has a lower  error in the Orange County Coastline example, the density estimation fails to give a good indication of regions of high and low likelihood.
error in the Orange County Coastline example, the density estimation fails to give a good indication of regions of high and low likelihood.
 error comparison of the three methods for the Orange County Coastline example shown in Figures 7, 8, and 9. Our proposed methods performed better than the Kernel density estimation method.
error comparison of the three methods for the Orange County Coastline example shown in Figures 7, 8, and 9. Our proposed methods performed better than the Kernel density estimation method.6.4. Residential Burglary Example
The following example uses actual residential burglary information from the San Fernando Valley in Los Angeles. Figure 10 is the area of interest and the locations of 4,487 burglaries that occurred in the region during 2004 and 2005. The aerial image was obtained using Google earth. We assume that residential burglaries cannot occur in large parks, lakes, mountainous areas without houses, airports, and industrial areas. Using census or other types of data, housing density information for a given region can be calculated. Figure 10(c) is the housing density for our region of interest. The housing density provides us with the exact locations of where residential burglaries may occur. However, our methods prohibit the density estimates from spreading through the boundaries of the valid region. If we were to use this image directly as the valid region, then crimes on one side of a street will not have an effect on the opposite side of the road. Therefore, we fill in small holes and streets in the housing density image and use the image located in Figure 10(d) as our valid region.
These figures are for the San Fernando Valley residential burglary data. In (a), we have the aerial image of the region we are considering, which is about 16 km by 18 km. Figure (b) shows the residential burglaries of the region. Figure (c) gives the housing density for the San Fernando Valley. We show the valid region we obtained from the housing density in figure (d). (a) Google earth image of San Fernando Valley region, (b) San Fernando Valley residential burglary residential burglaries, (c) San Fernando Valley residential burglary housing density, (d) San Fernando Valley residential burglary valid region
Using our Weighted  MPLE and Modified TV MPLE models, the Gaussian Kernel Density Estimate with variance
MPLE and Modified TV MPLE models, the Gaussian Kernel Density Estimate with variance  , and the TV MPLE method, we obtained the density estimations shown in Figure 11.
, and the TV MPLE method, we obtained the density estimations shown in Figure 11.
These images are the density estimates for the San Fernando Valley residential burglary data. (a) and (b) show the results of the current methods Kernel Density Estimation and TV MPLE, respectively. The results from our Modified TV MPLE method and our Weighted H1 MPLE method are shown in figures (c) and (d), respectively. The color scale represents the number of residential burglaries per year per square kilometer., (a) San Fernando Valley residential burglary kernel density estimation, (b) San Fernando Valley residential burglary TV MPLE density estimation, (c) San Fernando Valley residential burglary modified TV MPLE density estimation, (d) San Fernando Valley residential burglary weighted H1 MPLE density estimation
7. Conclusions and Future Work
In this paper we have studied the problem of determining a more geographically accurate probability density estimate. We demonstrate the importance of this problem by showing how common density estimation techniques, such as Kernel Density Estimation, fail to restrict the support of the density in a set of realistic examples.
To handle this problem, we proposed a set of methods, based on Total Variation and  -regularized MPLE models, that demonstrates great improvements in accurately enforcing the support of the density estimate when the valid region has been provided a priori. Unlike the TV-regularized methods, our
-regularized MPLE models, that demonstrates great improvements in accurately enforcing the support of the density estimate when the valid region has been provided a priori. Unlike the TV-regularized methods, our  model has the advantage that it performs well for very sparse data sets.
model has the advantage that it performs well for very sparse data sets.
The effectiveness of the methods is shown in a set of examples in which burglary probability densities are approximated from a set of crime events. Regions in which burglaries are impossible, such as oceans, mountains, and parks, are determined using aerial images or other external spatial data. These regions are then used to define an invalid region in which the density should be zero. Therefore, our methods are used to build geographically accurate probability maps.
It is interesting to note that there appears to be a relationship in the ratio between the number of samples and the size of the grid. In fact, each model has shown very different behavior in this respect. The TV-based methods appear to be very sensitive to large changes in this ratio, whereas the  method seems to be robust to these same changes. We are uncertain about why this phenomenon exists, and this would make an interesting future research topic.
method seems to be robust to these same changes. We are uncertain about why this phenomenon exists, and this would make an interesting future research topic.
There are many directions in which we can build on the results of this paper. We would like to devise better methods for determining the valid region, possibly evolving the edge set of the valid region using  -convergence [17]. Since this technique can be used for many types of event data, including residential burglaries, we would also like to apply this method to Iraq Body Count Data. Finally, we would like to handle possible errors in the data, such as incorrect positioning of events that place them in the invalid region, by considering a probabilistic model of their position.
-convergence [17]. Since this technique can be used for many types of event data, including residential burglaries, we would also like to apply this method to Iraq Body Count Data. Finally, we would like to handle possible errors in the data, such as incorrect positioning of events that place them in the invalid region, by considering a probabilistic model of their position.
References
Kim Rossmo D: Geographic Profiling. CRC Press; 2000.
Mohler GO, Short MB: Geographic profiling from kinetic models of criminal behavior. in review
O'Leary M: The mathematics of geographic profiling. Journal of Investigative Psychology and Offender Profiling 2009, 6: 253-265. 10.1002/jip.111
Silverman BW: Kernel density estimation using the fast fourier transform. Applied Statistics, Royal Statistical Society 1982, 31: 93-97.
Silverman BW: Density Estimation for Statistics and Data Analysis. Chapman & Hall/CRC; 1986.
Davies PL, Kovac A: Densities, spectral densities and modality. Annals of Statistics 2004, 32(3):1093-1136. 10.1214/009053604000000364
Kooperberg C, Stone CJ: A study of logspline density estimation. Computational Statistics and Data Analysis 1991, 12(3):327-347. 10.1016/0167-9473(91)90115-I
Sardy S, Tseng P:Density estimation by total variation penalized likelihood driven by the sparsity
 information criterion. Scandinavian Journal of Statistics 2010, 37(2):321-337. 10.1111/j.1467-9469.2009.00672.x
information criterion. Scandinavian Journal of Statistics 2010, 37(2):321-337. 10.1111/j.1467-9469.2009.00672.xKoenker R, Mizera I: Density estimation by total variation regularization. In Advances in Statistical Modeling and Inference, Essays in Honor of Kjell A. Doksum. World Scientific; 2007:613-634.
Mohler GO, Bertozzi AL, Goldstein TA, Osher SJ: Fast TV regularization for 2D maximum penalized likelihood estimation. to appear in Journal of Computational and Graphical Statistics
Eggermont PPB, LaRiccia VN: Maximum Penalized Likelihood Estimation. Springer, Berlin, Germany; 2001.
Goodd IJ, Gaskins RA: Nonparametric roughness penalties for probability densities. Biometrika 1971, 58(2):255-277.
Rudin LI, Osher S, Fatemi E: Nonlinear total variation based noise removal algorithms. Physica D 1992, 60(1–4):259-268.
Moeller M, Wittman T, Bertozzi AL: Variational wavelet pan-sharpening. In CAM Report. UCLA; 2008.
Ballester C, Caselles V, Igual L, Verdera J, Rougé B:A variational model for
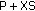 image fusion. International Journal of Computer Vision 2006, 69(1):43-58. 10.1007/s11263-006-6852-x
image fusion. International Journal of Computer Vision 2006, 69(1):43-58. 10.1007/s11263-006-6852-xMumford D, Shah J: Optimal approximations by piecewise smooth functions and associated variational problems. Communications on Pure and Applied Mathematics 1989, 42(5):577-685. 10.1002/cpa.3160420503
Ambrosio L, Tortorelli VM:Approximation of functional depending on jumps by elliptic functional via
 - convergence. Communications on Pure and Applied Mathematics 1990, 43(8):999-1036. 10.1002/cpa.3160430805
- convergence. Communications on Pure and Applied Mathematics 1990, 43(8):999-1036. 10.1002/cpa.3160430805Osher S, Burger M, Goldfarb D, Xu J, Yin W: An iterative regularization method for total variation-based image restoration. Multiscale Modeling and Simulation 2005, 4(2):460-489. 10.1137/040605412
Goldstein T, Osher S: Split bregman method for L1 regularized problems. SIAM Journal on Imaging Sciences 2009, 2: 323-343. 10.1137/080725891
Wang Y, Yang J, Yin W, Zhang Y: A new alternating minimization algorithm for total variation image reconstruction. SIAM Journal on Imaging Sciences 2008, 1(3):248-272. 10.1137/080724265
Acknowledgments
This work was supported by NSF Grant BCS-0527388, NSF Grant DMS-0914856, ARO MURI Grant 50363-MA-MUR, ARO MURI Grant W911NS-09-1-0559, ONR Grant N000140810363, ONR Grant N000141010221, and the Department of Defense. The authors would like to thank George Tita and the LAPD for the burglary data set. They would also like to thank Jeff Brantingham, Martin Short, and the IPAM RIPS program at UCLA for the housing density data, which was obtained using ArcGIS and the LA County tax assessor data. They obtained our aerial images from Google Earth.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Smith, L.M., Keegan, M.S., Wittman, T. et al. Improving Density Estimation by Incorporating Spatial Information. EURASIP J. Adv. Signal Process. 2010, 265631 (2010). https://doi.org/10.1155/2010/265631
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/265631

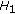 Sobolev MPLE Model
Sobolev MPLE Model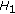 MPLE Implementation
MPLE Implementation









 information criterion. Scandinavian Journal of Statistics 2010, 37(2):321-337. 10.1111/j.1467-9469.2009.00672.x
information criterion. Scandinavian Journal of Statistics 2010, 37(2):321-337. 10.1111/j.1467-9469.2009.00672.x image fusion. International Journal of Computer Vision 2006, 69(1):43-58. 10.1007/s11263-006-6852-x
image fusion. International Journal of Computer Vision 2006, 69(1):43-58. 10.1007/s11263-006-6852-x - convergence. Communications on Pure and Applied Mathematics 1990, 43(8):999-1036. 10.1002/cpa.3160430805
- convergence. Communications on Pure and Applied Mathematics 1990, 43(8):999-1036. 10.1002/cpa.3160430805