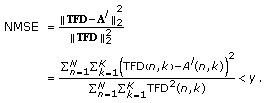- Research Article
- Open access
- Published:
Time-Frequency Data Reduction for Event Related Potentials: Combining Principal Component Analysis and Matching Pursuit
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 289571 (2010)
Abstract
Joint time-frequency representations offer a rich representation of event related potentials (ERPs) that cannot be obtained through individual time or frequency domain analysis. This representation, however, comes at the expense of increased data volume and the difficulty of interpreting the resulting representations. Therefore, methods that can reduce the large amount of time-frequency data to experimentally relevant components are essential. In this paper, we present a method that reduces the large volume of ERP time-frequency data into a few significant time-frequency parameters. The proposed method is based on applying the widely used matching pursuit (MP) approach, with a Gabor dictionary, to principal components extracted from the time-frequency domain. The proposed PCA-Gabor decomposition is compared with other time-frequency data reduction methods such as the time-frequency PCA approach alone and standard matching pursuit methods using a Gabor dictionary for both simulated and biological data. The results show that the proposed PCA-Gabor approach performs better than either the PCA alone or the standard MP data reduction methods, by using the smallest amount of ERP data variance to produce the strongest statistical separation between experimental conditions.
1. Introduction
Event-related potential (ERP) signals measured at the scalp are produced by partial synchronization of neuronal field potentials across the cortex [1]. This synchronization mediates the "top-down" and "bottom-up" communication both within and between brain areas and has particular importance during the anticipation of and attention to stimuli or events. Event related potentials (ERPs) are obtained by averaging EEG signals recorded over multiple trials or epochs time-locked to the particular stimulus. ERP signal analysis has proven to be effective in assessing the brain's current functional state and reflect many pathological processes (e.g., [2–6]).
Typically, ERP analysis is performed in the time domain, where the amplitudes and latencies of prominent peaks in the averaged potentials are usually measured and correlated with information processing mechanisms. However, this conventional approach has two major shortcomings. First, it is well-known that ERPs are transient and nonstationary signals. Second, ERPs generally contain multiple overlapping processes operating across different time and frequency ranges. A primary approach to this problem has been to utilize time-frequency signal representations to detect transient activity and to disentangle overlapping processes. Several methods exist to fulfill this goal including wavelet and wavelet packet decomposition [7–11], sparse signal representations using overcomplete dictionaries (such as matching pursuit [12, 13] and basis pursuit [14]), Cohen's class of time-frequency distributions [15, 16], and the recently introduced high resolution time-frequency distributions [17–20].
Wavelet transforms have been successfully applied to the analysis of evoked potentials in a variety of studies [4, 7, 21]. They have been shown to be advantageous over the Fourier transform, since the time varying frequency information can be observed. However, wavelets have well-known limitations in terms of time-frequency resolution tradeoff, that is, at high frequencies, the temporal resolution is high whereas the frequency resolution is low and vice versa for low frequencies. Sparse representations such as matching pursuit and basis pursuit aim to find a "best" fit to the given signal in terms of the elements of a redundant family of functions, called the dictionary [12, 13]. The "best" fit to the given signal is quantified through both the mean square error between the representation and the actual signal and the sparseness of the representation, that is, the number of elements of the dictionary used in the representation should be minimal. This approach has the advantage of offering a fully quantitative description of the ERPs by parameterizing the time-frequency plane at the expense of being computationally expensive. Cohen's class of distributions provides advantages over the other time-frequency representations in that it accurately characterizes the physical time-frequency properties of a signal, for example, energy and marginals, and yields uniformly high resolution over the entire time-frequency plane [15, 22]. Recently, time-frequency distributions with improved resolution and concentration around the instantaneous frequency have been introduced such as the reassigned time-frequency representations, higher order polynomial distributions, and complex-lag distributions [17, 20, 23]. Although these methods improve the resolution of the representations, they come at the expense of increased computational complexity and in some cases losing some of the desirable properties such as the marginals. Moreover, these distributions have been shown to be the most effective for polynomial phase signals whereas ERPs have been shown to be well represented by damped sinusoids [24], thus the improvement provided by these more complex distributions would be minimal. For these reasons, in this paper we will focus on the Cohen's class of distributions, in particular the Reduced Interference Distributions.
The high resolution provided by Cohen's class of time-frequency distributions come at the expense of increased data. The application of these distributions to large sets of ERP data has tended to rely on a time-frequency region of interest (TF-ROI; region of interest on the TF surface) to define activity for evaluation. Therefore, there is a growing need for data reduction and feature extraction methods for reducing the three dimensional time-frequency surfaces of ERPs to a few parameters. The problem of feature extraction and data reduction has been traditionally addressed using parametric and nonparametric methods. Parametric approaches include sparse representations using overcomplete dictionaries [12–14, 25–28], extraction of features from the time-frequency distributions such as the energy in different frequency bands, computation of higher order joint moments [29, 30], and entropy [31]. Non-parametric data reduction methods, on the other hand, include data-driven multivariate component analysis such as the application of matrix factorization methods to time-frequency distributions. These methods include the nonnegative matrix factorization (NMF) [32–34], singular value decomposition (SVD) [35], independent component analysis (ICA) [1, 36], and principal component analysis (PCA) [37–40] to extract time-frequency features for classification purposes or for reducing the time-frequency surfaces to a few meaningful components. The application of the matrix factorization approaches have been mostly limited to decomposing a single time-frequency matrix into significant time and frequency components to reduce the dimensionality and extract features for consequent classification [34, 39]. However, in ERP analysis there is a need for multivariate processing, that is, it is important to extract components that describe a collection of signals, such as those collected over multiple channels or multiple subjects. The principal component analysis of time-frequency vectors representing multiple subjects described in [37, 41] addresses this issue by extracting time-frequency principal components over a collection of ERP waveforms. At this point, it is also important to motivate the use of PCA over other data factorization methods. PCA is a multivariate technique that seeks to uncover latent variables responsible for patterns of covariation in the data set and has been used widely for time domain ERP data description and reduction [42, 43]. It is commonly applied to the covariance of the data matrix and is thus similar to SVD in the extracted components. PCA does not make any strong assumptions about the data, unlike NMF which imposes nonnegativeness, with the only assumption being that the observations are linear functions of the extracted components which is a common assumption in ERP analysis. ICA has been proposed as a promising alternative to PCA for ERP data reduction [1, 36]. However, recent comparisons of PCA with ICA for ERP data analysis indicates that ICA suffers from the component "splitting" problem, that is, components that should not be separated are split into multiple components, and that it is more suitable for spatial decompositions rather than temporal ones [44, 45]. Further, ICA has been most commonly applied to time-domain ERP signal representations, and its use with time-frequency ERP representations has not been well-validated. For these reasons, in the current paper we use PCA as the first step in our data reduction algorithm.
In this paper, we address the data extraction and reduction problem in the time-frequency plane by combining parametric and nonparametric methods in a nonstationary setting. The ultimate goal is to find time-frequency components that are common to a large set of ERP data and that can summarize the relevant activity in terms of a few parameters. We introduce a new data reduction method based on applying matching pursuit decomposition to the time-frequency domain principal components to further reduce the information from the principal components and to fully quantify the time-frequency parameters of ERPs. Since the principal components extracted from ERP time-frequency surfaces are well-localized in time and frequency, we propose quantifying them in terms of well-known compact signals, Gabor logons (in this paper, "Gabor logons" and "logons" will be used interchangeably), on the time-frequency plane. Even though there are various choices for the basis functions that can be used to decompose a given signal, in this paper Gabor logons are chosen for representing time-frequency structure of ERP signals for two major reasons. First, it is known that these functions achieve the lower bound of the uncertainty principle (time-bandwidth product) and have been described as the "elementary signals" on the time-frequency plane [22, 46]. Second, the parameters of the Gabor logons are well-suited for identifying between transient versus oscillatory brain activity as well as separating between overlapping time-frequency events with varying duration or frequency oscillation. They have been widely used in time-frequency representation of ERP signals [47–49], in particular EEG phenomena including sleep spindles [13, 50] and epileptic seizures [51]. An algorithm similar to matching pursuit is developed in the time-frequency plane to determine the best set of logons that describe each ERP time-frequency principal component [12]. Fitting Gabor logons to the extracted principal components offers three potential benefits. First, decomposing the principal components (PCs) into a few logons would capture the major activity described by that principal component while at the same time serve as a tool of denoising, that is, removing the unwanted noise or activity that may exist in the principal component. Second, insofar as a single logon can characterize the primary activity in the experimental manipulations for each principal component, this would offer evidence that the principal components approach is efficient at extracting compact time-frequency representations. Finally, the extracted logons offer an important unit of analysis in their own right, in that they are maximally compact by definition. The proposed methods are compared to both parametric and nonparametric data reduction methods in the time-frequency plane, namely, the standard matching pursuit algorithm [12, 52] and PCA in terms of efficiency, computational complexity and the effectiveness in describing the experimental effects in the data. To evaluate these methods, we employ both biological [41] and simulated data [37], that have been previously evaluated using the PCA on the time-frequency plane approach.
The rest of this paper is organized as follows. Section 2 gives a brief review of time-frequency distributions and various matching pursuit approaches. Section 3 introduces the data reduction method proposed in this paper, combining principal component analysis with matching pursuit on the time-frequency plane. Section 4 details the data analyzed in this paper and presents the results of applying the proposed method to both simulated data and ERP signals. A comparison with different time-frequency data reduction methods is also given in this section. Finally, Section 5 concludes the paper and discusses the major contributions.
2. Background
2.1. Time-Frequency Distributions
A bilinear time-frequency distribution (TFD),  , from Cohen's class can be expressed as (all integrals are from
, from Cohen's class can be expressed as (all integrals are from  to
to  unless otherwise stated) [22]
unless otherwise stated) [22]

where  is the kernel function in the ambiguity domain (
is the kernel function in the ambiguity domain ( ),
),  is the signal, and
is the signal, and  and
and  are the time and the frequency variables, respectively. Some of the most desired properties of TFDs are the energy preservation, the marginals, and the reduced interference. For bilinear time-frequency distributions, cross-terms occur when the signal is multicomponent, that is, if
are the time and the frequency variables, respectively. Some of the most desired properties of TFDs are the energy preservation, the marginals, and the reduced interference. For bilinear time-frequency distributions, cross-terms occur when the signal is multicomponent, that is, if  then
then  , where
, where  and
and  refer to the autoterms and cross-terms, respectively. The cross-terms will introduce time-frequency structures that do not correspond to the time-frequency spectrum of the actual signal. For this reason, in this paper we will use reduced interference distributions (RIDs) that concentrate the energy across the autoterms, satisfy the energy preservation and the marginals [53].
refer to the autoterms and cross-terms, respectively. The cross-terms will introduce time-frequency structures that do not correspond to the time-frequency spectrum of the actual signal. For this reason, in this paper we will use reduced interference distributions (RIDs) that concentrate the energy across the autoterms, satisfy the energy preservation and the marginals [53].
2.2. Matching Pursuit
The matching pursuit algorithm, originally proposed by Mallat, aims at obtaining the "best" linear representation of a signal in terms of functions,  (sometimes referred to as atoms), from an overcomplete dictionary,
(sometimes referred to as atoms), from an overcomplete dictionary,  , using an iterative search algorithm [12].
, using an iterative search algorithm [12].
-
(1)
Define the 0th order residual as
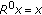 ,
, 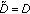 and set
and set 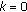 .
. -
(2)
For the
 th order residual,
th order residual, 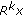 , select the best atom such that the inner product between the residual and the atom is maximized
, select the best atom such that the inner product between the residual and the atom is maximized  (2)
(2)
-
(3)
Compute the residue
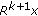 as
as 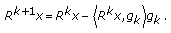 (3)
(3)
-
(4)
Set
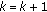 ,
, 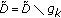 , and go back to step 2 until a predetermined stopping criterion is achieved. The stopping criterion can either be a preselected number of atoms to describe the signal or a percentage of energy of the original signal described by the selected atoms. After
, and go back to step 2 until a predetermined stopping criterion is achieved. The stopping criterion can either be a preselected number of atoms to describe the signal or a percentage of energy of the original signal described by the selected atoms. After 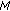 iterations, the following linear representation is obtained:
iterations, the following linear representation is obtained:  (4)
(4)
This procedure converges to  in the limit, that is,
in the limit, that is,  , and preserves signal energy.
, and preserves signal energy.
2.3. Simultaneous Matching Pursuit
The principle of MP can easily be generalized to the simultaneous decomposition of multiple signals,  , into atoms from the same overcomplete dictionary,
, into atoms from the same overcomplete dictionary,  . This approach is sometimes referred to as the multichannel matching pursuit or the multivariate matching pursuit (MMP) algorithm in literature since it is usually applied to multiple signals collected over multiple channels or sensors [52, 54–56]. In this paper, we will refer to this method as the simultaneous matching pursuit (SMP) to avoid any confusions since the method will be applied to multiple ERPs from different subjects and not from multiple channels. This algorithm can be described as follows.
. This approach is sometimes referred to as the multichannel matching pursuit or the multivariate matching pursuit (MMP) algorithm in literature since it is usually applied to multiple signals collected over multiple channels or sensors [52, 54–56]. In this paper, we will refer to this method as the simultaneous matching pursuit (SMP) to avoid any confusions since the method will be applied to multiple ERPs from different subjects and not from multiple channels. This algorithm can be described as follows.
-
(1)
Define for each signal
 the 0th order residual as
the 0th order residual as 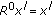 and set
and set 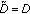 ,
,  .
. -
(2)
For the
 th order residual,
th order residual,  , select the best atom such that the sum of the squared inner products between the atom and the residual from each signal is maximized
, select the best atom such that the sum of the squared inner products between the atom and the residual from each signal is maximized 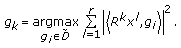 (5)
(5)
-
(3)
Compute the residue
 for each signal:
for each signal:  (6)
(6)
-
(4)
Set
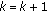 ,
, 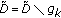 , and go back to step 2 until a predetermined stopping criterion is achieved. The stopping criterion can either be a preselected number of atoms to describe the collection of signals or an average percentage of energy of the original signals described by the selected atoms. After
, and go back to step 2 until a predetermined stopping criterion is achieved. The stopping criterion can either be a preselected number of atoms to describe the collection of signals or an average percentage of energy of the original signals described by the selected atoms. After 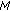 iterations, the following linear representation is obtained for each signal:
iterations, the following linear representation is obtained for each signal: 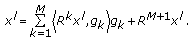 (7)
(7)
3. PCA-Gabor Method
Ideally, a time-frequency domain ERP data reduction method will faithfully reproduce established time and frequency-based findings (i.e., peaks in the time domain such as P300 or summaries of frequency activity such as alpha), and also allow a more complex view of these phenomena using the joint time-frequency information available in the TFDs. The decomposition method used in this paper is based on two stages of consecutive data reduction. The first stage is a direct extension of PCA into the joint time-frequency domain and the second stage is the parametrization of the time-frequency principal components using a matching pursuit type algorithm.
3.1. PCA on the Time-Frequency Plane
The first stage of the algorithm extends principal component analysis to the time-frequency plane as follows.
-
(1)
Compute the time-frequency distribution of each ERP waveform from multiple subjects,
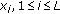 :
:  (8)
(8)where
 is the discrete-time kernel in the time and time-lag domain and
is the discrete-time kernel in the time and time-lag domain and  is the
is the  th ERP waveform. In this paper, the binomial kernel, given by
th ERP waveform. In this paper, the binomial kernel, given by (9)
(9)is used as the time-frequency kernel.
-
(2)
Given
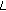 ERP waveforms, rearrange the time-frequency surfaces into vectors and form the matrix
ERP waveforms, rearrange the time-frequency surfaces into vectors and form the matrix 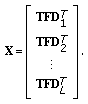 (10)
(10)
-
(3)
Compute the covariance matrix,
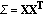 .
. -
(4)
Decompose the covariance matrix using principal component analysis
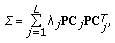 (11)
(11)where
 is the eigenvalue of each principal component
is the eigenvalue of each principal component 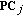 . The principal components determine the span of the time-frequency space.
. The principal components determine the span of the time-frequency space. -
(5)
Rotate the principal components using varimax rotation [57]. Varimax rotation is an orthogonal transform that rotates the principal components such that the variance of the factors is maximized. This rotation improves the interpretability of the principal components.
-
(6)
Rearrange each principal component into a time-frequency surface to obtain the ERP components in the time-frequency domain.
After the principal components on the time-frequency plane are extracted, they are ordered based on their eigenvalues and the most significant ones are used in the following parametrization stage. The number of principal components to keep is determined based on a normalized energy threshold.
3.2. Matching Pursuit on the Time-Frequency Plane
In this section, we introduce a matching pursuit type algorithm in the time-frequency domain to further parameterize the ERP time-frequency surfaces. The goal is to be able to describe the principal components using a compact set of time-frequency parameters using Gabor logons as the dictionary elements. The proposed algorithm is similar to the original matching pursuit [12] and the discrete Gabor decomposition [58], except that it is directly implemented in the time-frequency domain rather than in the time domain. This implementation is preferred over the standard MP for two reasons. First, the principal components are already in the time-frequency domain, and inverting them back to the time domain would increase the computational complexity. Second, this offers a way of directly modeling the time-frequency energy distribution.
An overcomplete dictionary of Gabor logons on the time-frequency plane is constructed by computing the time-frequency distribution of discrete time atoms  where
where  is the scale parameter,
is the scale parameter,  and
and  are the discrete time and frequency shift parameters, respectively, and
are the discrete time and frequency shift parameters, respectively, and  is the total number of frequency samples. The elements of the dictionary,
is the total number of frequency samples. The elements of the dictionary,  , are the binomial TFDs of these atoms,
, are the binomial TFDs of these atoms,  . The number of elements in the dictionary are determined by the range of
. The number of elements in the dictionary are determined by the range of  ,
,  and
and  . In this paper,
. In this paper,  , where
, where  is the total number of time samples,
is the total number of time samples,  , where
, where  is the total number of frequency samples, and
is the total number of frequency samples, and  .
.
The proposed greedy search algorithm is an extension of the orthogonal matching pursuit (OMP) described in [59] to the time-frequency domain. The orthogonal matching pursuit adds a least-squares minimization to each step of MP to obtain the best approximation over the atoms that have already been chosen. This revision significantly improves the convergence speed of the algorithm. For a given time-frequency matrix,  , the search for logons that best describe the surface can be summarized as follows.
, the search for logons that best describe the surface can be summarized as follows.
-
(1)
Initialize the residue as
 and set
and set 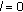 and
and  .
. -
(2)
At the
 th iteration, find the Gabor logon over the whole overcomplete dictionary, that is, over all
th iteration, find the Gabor logon over the whole overcomplete dictionary, that is, over all  , that has the largest inner product with the residue time-frequency surface,
, that has the largest inner product with the residue time-frequency surface, 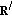
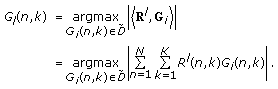 (12)
(12)
-
(3)
Compute the approximation at the
 th step,
th step, 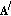 , as
, as 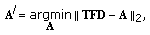 (13)
(13)
where  . This problem is solved using a least squares optimization approach.
. This problem is solved using a least squares optimization approach.
-
(4)
Subtract the approximation,
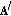 , from the residue to compute the new residue time-frequency distribution at the
, from the residue to compute the new residue time-frequency distribution at the 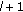 th iteration
th iteration 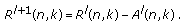 (14)
(14)
-
(5)
Increment
 by 1, set
by 1, set  .
. -
(6)
Go back to step 2 until a predetermined number of atoms is selected or the normalized mean squared error (NMSE) between the
 and the approximation at the lth iteration is below a predetermined threshold, that is,
and the approximation at the lth iteration is below a predetermined threshold, that is, 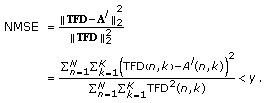 (15)
(15)
NMSE is a measure of how close the approximation from the dictionary is to the original time-frequency distribution. Since the mean square error is normalized by the energy of the original TFD, it is always between 0 and 1.
4. Simulated and Biological Data Analysis
4.1. Description of Biological Data
The biological data used in this paper has been previously presented utilizing PCA on the time-frequency plane approach, and thus we will only detail the relevant parameters here. The reader is directed to the previously published paper for greater detail [41]. The sample consisted of twins in the Minnesota Twin Family Study (MTFS), a longitudinal and epidemiological investigation of the origins and development of substance use disorders and related psychopathology. All male and female twin participants for whom ERP data were available from the study's psychophysiological assessment served as subjects for this investigation. This sample combined subjects from the two age cohorts of the MTFS. Subjects in one cohort were 17 years old at intake whereas subjects in the other were approximately 11 years old at intake. Data for this younger cohort came from a follow-up assessment conducted when subjects were approximately 17 years old. The sample thus comprised 2,068 17-year-old adolescents in all (mean age = 17.7; SD = 0.5; range = 16.7 to 20.0).
A visual oddball task was used. Each of the 240 stimuli comprising this task was presented on a computer screen for 98 ms, with the intertrial interval (ITI) varying randomly between 1 and 2 s. A small dot, upon which subjects were instructed to fixate, appeared in the center of the screen during the ITI. On twothirds of the trials, participants saw a plain oval to which they were instructed not to respond. On the remaining third of the trials, participants saw a superior view of a stylized head, depicting the nose and one ear. These stylized heads served as "target" stimuli. Participants were instructed to press one of two response buttons attached to each arm of their chair to indicate whether the ear was on the left side of the head or the right. Half of these target trials consisted of heads with the nose pointed up, such that the left ear would be on the left side of the head as it appeared to the subject (easy discrimination). Half consisted of heads rotated 180 degrees so that the nose pointed down, such that the left ear would appear on the right side of the screen and the right ear would appear on the left side of the ear (hard discrimination).
For each trial, 2 s of EEG, including a 500 ms prestimulus baseline, were collected at a sampling rate of 256 Hz. EEG data were recorded from three parietal scalp locations, one on the midline (Pz) and one over each hemisphere (P3 and P4). Consistent with the previous report, only data from the Pz electrode is reported here. Similarly, although ERPs to standard (frequent) stimuli were collected, they were not analyzed for the current paper; target condition responses serve as the basis for all decompositions and analyses presented. Therefore, the analysis in this paper focuses on data reduction for ERPs collected across multiple subjects from a single channel. However, the methods developed can easily be extended to single subject and/or multiple channel data.
Principal component decompositions were employed to evaluate the proposed approach. For the purposes of this study, decompositions for condition-averaged data were conducted on narrow time and frequency ranges, to focus on lower frequency delta and theta activity. Condition-averaged ERPs were constructed separately for easy and hard discrimination conditions. These included frequencies ranging from 0 to 5.75 Hz and time ranging from stimulus onset to 1000 ms poststimulus. The range was narrowed to focus on the time-frequency range containing the majority of variance: theta, delta, and low frequency activity.
4.2. Description of Simulated Data
Two simulated datasets were employed in the current paper. As with the biological data, these datasets were employed previously with PCA approach alone [37]. Briefly, the two sets included are 3-logons and 3-logons with noise. All simulated sets were 100 Hz sampled signals of 1000 ms, with the first and last 100 ms discarded after the TFD is computed to remove edge effects. The first simulated dataset contains 3 logons with clearly separated time and frequency centers: 30 Hz/100 ms, 20 Hz/400 ms, and 10 Hz/700 ms. For 3-logons with noise, noise was added at the 4 dB signal to noise level. In all simulations, each signal entered was assigned to a different simulated topographical region, to simulate the activity from different brain areas. To accomplish this, the signals were divided into 63 simulated channels creating a  grid within which differential weightings could be applied. Each signal entered, that is, each logon, was weighted by a
grid within which differential weightings could be applied. Each signal entered, that is, each logon, was weighted by a  grid differentially located within the overall
grid differentially located within the overall  grid. The differential loadings were implemented to simulate a signal with more focal activity that decays in topographic space. The simulated datasets each contained 7560 total waveforms, comprised of 120 trials by 63 electrodes.
grid. The differential loadings were implemented to simulate a signal with more focal activity that decays in topographic space. The simulated datasets each contained 7560 total waveforms, comprised of 120 trials by 63 electrodes.
4.3. Results
In this section, we will present the results of applying the PCA-Gabor method on both simulated data and ERP signals described above. In the PCA-Gabor analysis, we will focus on extracting the "best" logon fit to the principal component surface. Extracting the "best" logon offers a way of parameterizing the PCs using the time, frequency and scale parameters of the logon as well as serving as a denoising tool since the "best" logon will focus on representing the actual signal energy as opposed to background noise. Through this analysis, we will show the effectiveness of the PCA-Gabor method both as a modeling/data reduction tool and a denoising tool. The proposed method also offers an alternative to previous ERP studies that use matching pursuit to decompose each signal individually [13]. This analysis has the disadvantage of being computationally expensive and extracting a large number of logons to represent a collection of signals. Since a comparison between matching pursuit at the individual signal level and the PCA-Gabor method would not be helpful due the number of logons extracted being much larger for the MP, we compare the PCA-Gabor method to the simultaneous matching pursuit with Gabor dictionary (SMP-Gabor) and to previous results obtained by the PCA method on the time-frequency plane [37].
4.3.1. Analysis of Simulated Data
The different methods were first evaluated for simulated data made up of Gabor logons. For this analysis, decompositions from two simulated datasets containing 3-logons with and without additive white noise were used. The PCA approach involved selecting the three time-frequency PCs with the highest eigenvalues. The PCA-Gabor approach extracted the "best" Gabor logon for each of the three PCs yielding three logons. Finally, the SMP-Gabor method extracted the best three logons that explained the whole data set. For the 3-logons without noise all of the methods explained more than  variance of the data set with the PCA performing the best (Table 1). The logons extracted from PCA-Gabor and SMP-Gabor were identical (see Figure 1) explaining exactly the same amount of data variance indicating that under ideal conditions PCA-Gabor performs as well as the standard SMP-Gabor.
variance of the data set with the PCA performing the best (Table 1). The logons extracted from PCA-Gabor and SMP-Gabor were identical (see Figure 1) explaining exactly the same amount of data variance indicating that under ideal conditions PCA-Gabor performs as well as the standard SMP-Gabor.
For 3-logons in 4 dB noise, similarly, three components were extracted by each of the algorithms, that is, three PCs with PCA, three logons fitted to the PCs with PCA-Gabor, and three logons fitted to the whole dataset with SMP-Gabor. The extracted components were evaluated in terms of the amount of signal variance they captured by projecting the components onto the original 3-logon dataset. From Table 1, it can be seen that PCA-Gabor captures the most amount of signal variance with PCA coming in second. The logons extracted from the SMP-Gabor method can only explain  of the total signal variance since the algorithm focuses on extracting components that capture the most amount of common variance in the data (whereas PCA is covariance-based), which in this case corresponds to noise. Figure 1 illustrates how the logons extracted by SMP-Gabor become wider in time and less correlated with the actual logons for the noisy data. This figure also shows that PCA-Gabor acts as a denoising mechanism reducing the noise in the PCs and thus representing more of the signal.
of the total signal variance since the algorithm focuses on extracting components that capture the most amount of common variance in the data (whereas PCA is covariance-based), which in this case corresponds to noise. Figure 1 illustrates how the logons extracted by SMP-Gabor become wider in time and less correlated with the actual logons for the noisy data. This figure also shows that PCA-Gabor acts as a denoising mechanism reducing the noise in the PCs and thus representing more of the signal.
4.3.2. Analysis of Biological Data
For the biological data, first we will compare the variance characterized using the different approaches. We extract 11 PCs using PCA, the 11 logons extracted from these PCs using PCA-Gabor, and 11 logons that best explain the energy of the whole dataset using the SMP-Gabor method. Once the different components are extracted, they are projected onto each of the 8328 condition-averaged ERP waveforms. For the three methods compared in this paper, PCA, PCA-Gabor and SMP-Gabor, PCA explained most of the data variance with 91%. For SMP-Gabor, the variance explained was 81% whereas for PCA-Gabor it was 70%.
While the PCA explains the most overall variance in the data, and PCA-Gabor the least, additional analysis is needed to evaluate the methods in terms of experimentally relevant variance. To accomplish this, the three methods were compared for statistical separation using three common variables: sex, reaction time, and task difficulty. Because the activity extracted from the three methods covers much of the same time-frequency range, it is expected that the three methods should provide similar statistical effects. Statistical evaluation was conducted using a repeated-measures general linear model (GLM) including sex, reaction time, and task difficulty. A separate GLM was conducted for the sets of 11 components from each method. The design was Sex (male/female) by RT (reaction time; continuous) by task Difficulty (easy/hard; the within-subjects repeated measure). These main effects were highly significant for all three methods, confirming that similar experimentally relevant activity was extracted. Partial eta-squared ( ) values for the three methods are summarized in Table 2. Here, for sex, RT, and difficulty, the nominal order of the amount of experimentally relevant variance in the statistical effects was the same, largest in the PCA-Gabor, next in the PCA, and the least in the SMP-Gabor.
) values for the three methods are summarized in Table 2. Here, for sex, RT, and difficulty, the nominal order of the amount of experimentally relevant variance in the statistical effects was the same, largest in the PCA-Gabor, next in the PCA, and the least in the SMP-Gabor.
 ) values from a repeated-measures general linear model (GLM) for the three methods for ERP analysis. Multivariate tests indicate statistical values across all components. Note: *
) values from a repeated-measures general linear model (GLM) for the three methods for ERP analysis. Multivariate tests indicate statistical values across all components. Note: * , **
, ** , and *
, and * .
.By comparing the data reduction methods in terms of both overall data variance as well as experimentally relevant variance, stronger inferences can be made about how well the methods perform. In particular, the PCA-Gabor method captured the largest amount of experimentally relevant variance, while using the least amount of overall data variance. This is analogous to the results of the simulated data with noise, where the PCA-Gabor method extracted the most signal power in terms of experimentally relevant variance, while excluding the largest amount of noise power in terms of experimentally irrelevant variance. Thus, in these terms, the PCA-Gabor method was the most optimal among the three methods.
Finally, it is important to compare the different approaches in terms of computational complexity. All of the algorithms are run on a PC with Pentium 4 processor at 2 GHz using MATLAB 7.0, and evaluated after generating the time-frequency surfaces. The PCA-Gabor method took 11.6 seconds including the time to find the principal components (3.2 seconds) and to search for the best logon fit for the resulting PCs (8.4 seconds). The simultaneous matching pursuit on the other hand took 1276 seconds. Thus, in terms of computational complexity, PCA approach was the fastest, followed closely by the PCA-Gabor method. Trailing by a large margin is the SMP-Gabor method, which was computationally expensive due to the core search algorithm required.
Table 3 summarizes the key properties of the three methods compared in this section in terms of their data dependence, time and frequency parametrization, computational efficiency for the ERP data set and whether the resulting decomposition is based on explaining the most variance or covariance in the data.
4.4. Discussions
Several overall trends in the results are important to detail. First, the PCA-Gabor characterized more experimental variance than the PCA, with less of the overall raw data variance. This suggests that the Gabor decomposition of the PCA represents the relevant information obtained in the PCA, supporting the view that the activity extracted by PCA largely contains activity that conforms to Gabor constraints. Second, because the PCA-Gabor explains nominally more experimentally relevant variance, and outperforms the SMP-Gabor, while using less of the raw data variance than either, it supports the contention that this approach produces a more optimal Gabor decomposition of the collection of signals than the standard matching pursuit. Finally, it is interesting to specifically consider the fact that the PCA-Gabor method explains the least amount of data variance compared to the other two methods. The components extracted by PCA explain most of the data variance since PCA is designed to maximize the variance explained and extracts components that are orthogonal to each other. The PCA-Gabor method, on the other hand, approximates the energy of each principal component with a single logon and thus, the total variance explained is lower than the original principal components. However, this method has the advantage of retaining the signal variance and getting rid of the noise variance, thus acting as an effective denoising method, while also parameterizing the time-frequency surfaces. The third method, SMP-Gabor, explains more of the data variance compared to PCA-Gabor but has less experimental condition sensitivity (e.g., statistical significance). This increased variance and reduced sensitivity can be explained by looking at the Gabor logons extracted from the biological data by PCA-Gabor and SMP-Gabor methods shown in Figure 1. Although the two methods extract some common logons, SMP-Gabor method emphasizes the low frequency activity. The first three logons extracted by this method are low frequency logons with a large time spread. The major reason for this is that the SMP-Gabor method operates entirely on the variance, and thus focuses the most on the high-amplitude (i.e., variance) low-frequency area of the surface. The PCA approaches, on the other hand, operate on covariance, which focuses more on activity that is functionally related (i.e., covaries). This point is also supported by the Gabor decomposition of the grand average of the 8328 waveforms given in Figure 3. Table 4 compares the parameters of the 11 logons extracted from the 11 PCs using the PCA-Gabor method, from the 8238 TFD surfaces using the SMP-Gabor method and from the grand average of the 8238 waveforms using standard MP-Gabor. This table indicates that there are some commonalities between the SMP-Gabor and MP-Gabor on the grand average surface since they extract similar logons describing the low frequency activity, for example, logons 1-3 are almost identical.
 , frequency center (Hz),
, frequency center (Hz),  , and scale parameter
, and scale parameter  ) of the 11 logons extracted by PCA-Gabor from the 11 PCs, SMP-Gabor from the 8238 TFD surfaces, and MP-Gabor from the grand average of the 8238 time-frequency surfaces.
) of the 11 logons extracted by PCA-Gabor from the 11 PCs, SMP-Gabor from the 8238 TFD surfaces, and MP-Gabor from the grand average of the 8238 time-frequency surfaces.5. Conclusions
In this paper, a time-frequency data reduction method combining a nonparametric data-driven approach, principal component analysis, with a parametric approach, matching pursuit with a Gabor dictionary, was presented. Using the proposed method, it was possible to characterize large amounts of ERP data with a small number of time-frequency parameters. This joint application of PCA with Gabor decomposition offered several advantages over individual PCA and Gabor decomposition. First, compared to PCA the proposed method improves the SNR of the extracted components, that is, performs denoising, while simultaneously parameterizing the time-frequency surfaces and offering a succinct representation of the data set. Second, the application of Gabor decomposition onto the principal components instead of the actual data helps to extract parameters that represent the covariation among observations rather than characterize the average energy across observations. This property of PCA-Gabor becomes especially important when there is considerable noise in the data since standard matching pursuit algorithms will focus on fitting parameters to capture the most amount of energy, which in this case may be noise components. This phenomenon exhibited itself in the analysis of the biological data as PCA-Gabor most effectively differentiated between the experimental conditions with the least amount of data variance, or in other words capturing the least amount of noise, compared to the other two methods. This was mainly because the extracted logons explained the main effects described by the principal components with higher signal-to-noise ratio (most experimentally relevant variance).
Future work will focus on the extensions of the proposed methods to different data factorization approaches such as the ICA. For ERP data collected over multiple channels, spatial ICA may be used as an alternative to PCA and the proposed data reduction method can be applied onto the independent components. Future work will also evaluate the Gabor parameters in relation to well-known cognitive ERP events such as P300, as well as ERP events with known specific neurological origins, such as anterior cingulate cortex activation as measured in the error-related negativity (ERN) paradigm.
References
Makeig S, Debener S, Onton J, Delorme A: Mining event-related brain dynamics. Trends in Cognitive Sciences 2004, 8(5):204-210. 10.1016/j.tics.2004.03.008
Shevrin H, Bond JA, Brakel LA, Hertel RK, Williams WJ: Conscious and Unconscious Processes: Psychodynamic, Cognitive and Neurophysiological Convergences. Guilford Press, New York, NY, USA; 1996.
Shevrin H, Williams WJ, Marshall RE, Hertel RK, Bond JA, Brakel LA: Event-related potential indicators of the dynamic unconscious. Consciousness and Cognition 1992, 1(3):340-366. 10.1016/1053-8100(92)90068-L
Başar E: EEG-Brain Dynamics. Elsevier, Amsterdam, The Netherlands; 1980.
Sclabassi RJ, Sun M, Krieger DN, Jasiukaitis P, Scher MS: Time-frequency domain problems in the neurosciences. In Time-Frequency Signal Analysis: Methods and Applications. Edited by: Boashash B. Longman, Harlow, UK; 1992:498-519.
Williams WJ, Zaveri HP, Sackellares JC: Time-frequency analysis of electrophysiology signals in epilepsy. IEEE Engineering in Medicine and Biology 1995, 14(2):133-143. 10.1109/51.376750
Demiralp T, Yordanova J, Kolev V, Ademoglu A, Devrim M, Samar VJ: Time-frequency analysis of single-sweep event-related potentials by means of fast wavelet transform. Brain and Language 1999, 66(1):129-145. 10.1006/brln.1998.2028
Raz J, Dickerson L, Turetsky B: A wavelet packet model of evoked potentials. Brain and Language 1999, 66(1):61-88. 10.1006/brln.1998.2025
Samar VJ, Raghuveer MR, Swartz KP, Rosenberg S, Chaiyaboonthanit T: Wavelet decomposition of event related potentials: toward the definition of biologically natural components. Proceedings of the 6th IEEE Conference on Statistical Signal and Array Processing, 1992 38-41.
Herrmann CS, Grigutsch M, Busch NA: EEG Oscillations and Wavelet Analysis. MIT Press, Cambridge, Mass, USA; 2005.
Cranstoun SD, Ombao HC, Von Sachs R, Guo W, Litt B: Time-frequency spectral estimation of multichannel EEG using the auto-SLEX method. IEEE Transactions on Biomedical Engineering 2002, 49(9):988-996. 10.1109/TBME.2002.802015
Mallat SG, Zhang Z: Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing 1993, 41(12):3397-3415. 10.1109/78.258082
Durka PJ, Blinowska KJ: A unified time-frequency parametrization of EEGs. IEEE Engineering in Medicine and Biology 2001, 20(5):47-53. 10.1109/51.956819
Chen SS, Donoho DL, Saunders MA: Atomic decomposition by basis pursuit. SIAM Journal of Scientific Computing 1999, 20(1):33-61.
Williams WJ: Reduced interference distributions: biological applications and interpretations. Proceedings of the IEEE 1996, 84(9):1264-1280. 10.1109/5.535245
Haykin S, Racine RJ, Yan XU, Chapman CA: Monitoring neuronal oscillations and signal transmission between cortical regions using time-frequency analysis of electroencephalographic activity. Proceedings of the IEEE 1996, 84(9):1295-1301. 10.1109/5.535247
Shafi I, Ahmad J, Shah SI, Kashif FM: Techniques to obtain good resolution and concentrated time-frequency distributions: a review. EURASIP Journal on Advances in Signal Processing 2009, 2009:-43.
Shafi I, Ahmad J, Shah SI, Kashif FM: Computing deblurred time-frequency distributions using artificial neural networks. Circuits, Systems, and Signal Processing 2008, 27(3):277-294. 10.1007/s00034-008-9027-x
Shafi I, Ahmad J, Shah SI, Kashif FM: Evolutionary time-frequency distributions using Bayesian regularised neural network model. IET Signal Processing 2007, 1(2):97-106. 10.1049/iet-spr:20060311
Orović I, Stanković S: A class of highly concentrated time-frequency distributions based on the ambiguity domain representation and complex-lag moment. EURASIP Journal on Advances in Signal Processing 2009, 2009:-9.
Demiralp T, Ademoglu A, Comerchero M, Polich J: Wavelet analysis of P3a and P3b. Brain Topography 2001, 13(4):251-267. 10.1023/A:1011102628306
Cohen L: Time-Frequency Analysis. Prentice Hall, Upper Saddle River, NJ, USA; 1995.
Jachan M, Matz G, Hlawatsch F: Time-frequency ARMA models and parameter estimators for underspread nonstationary random processes. IEEE Transactions on Signal Processing 2007, 55(9):4366-4381.
Demiralp T, Ademoglu A, Istefanopulos Y, Gülçür HÖ: Analysis of event-related potentials (ERP) by damped sinusoids. Biological Cybernetics 1998, 78(6):487-493. 10.1007/s004220050452
Tropp JA: Greed is good: algorithmic results for sparse approximation. IEEE Transactions on Information Theory 2004, 50(10):2231-2242. 10.1109/TIT.2004.834793
Gribonval R: Fast matching pursuit with a multiscale dictionary of Gaussian chirps. IEEE Transactions on Signal Processing 2001, 49(5):994-1001. 10.1109/78.917803
Donoho DL, Huo X: Uncertainty principles and ideal atomic decomposition. IEEE Transactions on Information Theory 2001, 47(7):2845-2862. 10.1109/18.959265
Gorodnitsky IF, Rao BD: Sparse signal reconstruction from limited data using FOCUSS: a re-weighted minimum norm algorithm. IEEE Transactions on Signal Processing 1997, 45(3):600-616. 10.1109/78.558475
Tacer B, Loughlin PJ: Non-stationary signal classification using the joint moments of time-frequency distributions. Pattern Recognition 1998, 31(11):1635-1641. 10.1016/S0031-3203(98)00031-4
Krishnan S, Rangayyan RM, Bell GD, Frank CB: Adaptive time-frequency analysis of knee joint vibroarthrographic signals for noninvasive screening of articular cartilage pathology. IEEE Transactions on Biomedical Engineering 2000, 47(6):773-783. 10.1109/10.844228
Baraniuk RG, Flandrin P, Janssen AJEM, Michel OJJ: Measuring time-frequency information content using the Rényi entropies. IEEE Transactions on Information Theory 2001, 47(4):1391-1409. 10.1109/18.923723
Lee H, Cichocki A, Choi S: Nonnegative matrix factorization for motor imagery EEG classification. Lecture Notes in Computer Science 2006, 4132: 250-259. 10.1007/11840930_26
Mørup M, Hansen LK, Arnfred SM: ERPWAVELAB: a toolbox for multi-channel analysis of time-frequency transformed event related potentials. Journal of Neuroscience Methods 2007, 161(2):361-368. 10.1016/j.jneumeth.2006.11.008
Ghoraani B, Krishnan S: A joint time-frequency and matrix decomposition feature extraction methodology for pathological voice classification. EURASIP Journal on Advances in Signal Processing 2009, 2009:-11.
Hassanpour H, Mesbah M, Boashash B: Time-frequency feature extraction of newborn EEC seizure using SVD-based techniques. EURASIP Journal on Applied Signal Processing 2004, 2004(16):2544-2554. 10.1155/S1110865704406167
Jung T-P, Makeig S, Westerfield M, Townsend J, Courchesne E, Sejnowski TJ: Analysis and visualization of single-trial event-related potentials. Human Brain Mapping 2001, 14(3):166-185. 10.1002/hbm.1050
Bernat EM, Williams WJ, Gehring WJ: Decomposing ERP time-frequency energy using PCA. Clinical Neurophysiology 2005, 116(6):1314-1334. 10.1016/j.clinph.2005.01.019
Mayhew SD, Dirckx SG, Niazy RK, Iannetti GD, Wise RG: EEG signatures of auditory activity correlate with simultaneously recorded fMRI responses in humans. NeuroImage 2010, 49(1):849-864. 10.1016/j.neuroimage.2009.06.080
Englehart K, Hudgins B, Parker PA, Stevenson M: Classification of the myoelectric signal using time-frequency based representations. Medical Engineering and Physics 1999, 21(6-7):431-438. 10.1016/S1350-4533(99)00066-1
Iordanidou V, Michalopoulos K, Sakkalis V, Zervakis M: Decomposition methods for detailed analysis of content in ERP recordings. In Artificial Neural Networks–ICANN, Lecture Notes in Computer Science. Volume 5769. Springer, Berlin, Germany; 2009:368-377.
Bernat EM, Malone SM, Williams WJ, Patrick CJ, Iacono WG: Decomposing delta, theta, and alpha time-frequency ERP activity from a visual oddball task using PCA. International Journal of Psychophysiology 2007, 64(1):62-74. 10.1016/j.ijpsycho.2006.07.015
Dien J, Spencer KM, Donchin E: Localization of the event-related potential novelty response as defined by principal components analysis. Cognitive Brain Research 2003, 17(3):637-650. 10.1016/S0926-6410(03)00188-5
Spencer KM, Dien J, Donchin E: Spatiotemporal analysis of the late ERP responses to deviant stimuli. Psychophysiology 2001, 38(2):343-358. 10.1111/1469-8986.3820343
Dien J, Khoe W, Mangun GR: Evaluation of PCA and ICA of simulated ERPs: promax vs. infomax rotations. Human Brain Mapping 2007, 28(8):742-763. 10.1002/hbm.20304
Dien J: Evaluating two-step PCA of ERP data with geomin, infomax, oblimin, promax, and varimax rotations. Psychophysiology 2010, 47(1):170-183. 10.1111/j.1469-8986.2009.00885.x
Gabor D: Theory of communication. Journal of IEE 1946, 93: 429-457.
Brown ML, Williams WJ, Hero AO III: Non-orthogonal Gabor representation of event-related potentials. Proceedings of the 15th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, October 1993 314-315.
Zhang Z-G, Yang J-L, Chan S-C, Luk KD-K, Hu Y: Time-frequency component analysis of somatosensory evoked potentials in rats. BioMedical Engineering Online 2009., 8(1, article 4):
Bénar CG, Papadopoulo T, Torrésani B, Clerc M: Consensus matching pursuit for multi-trial EEG signals. Journal of Neuroscience Methods 2009, 180(1):161-170. 10.1016/j.jneumeth.2009.03.005
Schönwald SV, Gerhardt GJL, de Santa-Helena EL, Chaves MALF: Characteristics of human EEG sleep spindles assessed by Gabor transform. Physica A: Statistical Mechanics and its Applications 2003, 327(1-2):180-184. 10.1016/S0378-4371(03)00473-4
Jouny CC, Franaszczuk PJ, Bergey GK: Characterization of epileptic seizure dynamics using Gabor atom density. Clinical Neurophysiology 2003, 114(3):426-437. 10.1016/S1388-2457(02)00344-9
Gribonval R: Piecewise linear source separation. Wavelets: Applications in Signal and Image Processing X, August 2003, San Diego, Calif, USA, Proceedings of SPIE 5207: 297-310.
Jeong J, Williams WJ: Kernel design for reduced interference distributions. IEEE Transactions on Signal Processing 1992, 40(2):402-412. 10.1109/78.124950
Tropp JA, Gilbert AC, Strauss MJ: Algorithms for simultaneous sparse approximation. Part I: greedy pursuit. Signal Processing 2006, 86(3):572-588. 10.1016/j.sigpro.2005.05.030
Krstulović S, Gribonval R: MPTK: matching pursuit made tractable. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), May 2006 3: 496-499.
Studer D, Hoffmann U, Koenig T: From EEG dependency multichannel matching pursuit to sparse topographic EEG decomposition. Journal of Neuroscience Methods 2006, 153(2):261-275. 10.1016/j.jneumeth.2005.11.006
Kaiser HF: The varimax criterion for analytic rotation in factor analysis. Psychometrika 1958, 23(3):187-200. 10.1007/BF02289233
Qian S, Chen D: Discrete Gabor transform. IEEE Transactions on Signal Processing 1993, 41(7):2429-2438. 10.1109/78.224251
Pati YC, Rezaiifar R, Krishnaprasad PS: Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition. Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, 1993 1: 40-44.
Acknowledgments
This work was in part supported by Grants from the National Science Foundation under CAREER CCF-0746971, National Institutes of Health NIDA13240, NIDA05147, NIDA024417, NIAA09367, and K08MH080239.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Aviyente, S., Bernat, E.M., Malone, S.M. et al. Time-Frequency Data Reduction for Event Related Potentials: Combining Principal Component Analysis and Matching Pursuit. EURASIP J. Adv. Signal Process. 2010, 289571 (2010). https://doi.org/10.1155/2010/289571
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/289571
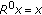 ,
, 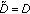 and set
and set 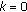 .
. th order residual,
th order residual, 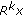 , select the best atom such that the inner product between the residual and the atom is maximized
, select the best atom such that the inner product between the residual and the atom is maximized 
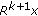 as
as 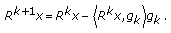
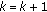 ,
, 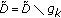 , and go back to step 2 until a predetermined stopping criterion is achieved. The stopping criterion can either be a preselected number of atoms to describe the signal or a percentage of energy of the original signal described by the selected atoms. After
, and go back to step 2 until a predetermined stopping criterion is achieved. The stopping criterion can either be a preselected number of atoms to describe the signal or a percentage of energy of the original signal described by the selected atoms. After 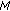 iterations, the following linear representation is obtained:
iterations, the following linear representation is obtained: 
 the 0th order residual as
the 0th order residual as 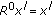 and set
and set 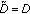 ,
,  .
. th order residual,
th order residual,  , select the best atom such that the sum of the squared inner products between the atom and the residual from each signal is maximized
, select the best atom such that the sum of the squared inner products between the atom and the residual from each signal is maximized 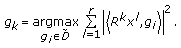
 for each signal:
for each signal: 
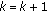 ,
, 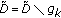 , and go back to step 2 until a predetermined stopping criterion is achieved. The stopping criterion can either be a preselected number of atoms to describe the collection of signals or an average percentage of energy of the original signals described by the selected atoms. After
, and go back to step 2 until a predetermined stopping criterion is achieved. The stopping criterion can either be a preselected number of atoms to describe the collection of signals or an average percentage of energy of the original signals described by the selected atoms. After 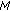 iterations, the following linear representation is obtained for each signal:
iterations, the following linear representation is obtained for each signal: 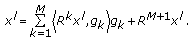
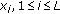 :
: 
 is the discrete-time kernel in the time and time-lag domain and
is the discrete-time kernel in the time and time-lag domain and  is the
is the  th ERP waveform. In this paper, the binomial kernel, given by
th ERP waveform. In this paper, the binomial kernel, given by
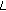 ERP waveforms, rearrange the time-frequency surfaces into vectors and form the matrix
ERP waveforms, rearrange the time-frequency surfaces into vectors and form the matrix 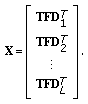
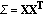 .
.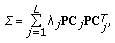
 is the eigenvalue of each principal component
is the eigenvalue of each principal component 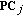 . The principal components determine the span of the time-frequency space.
. The principal components determine the span of the time-frequency space.  and set
and set 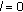 and
and  .
. th iteration, find the Gabor logon over the whole overcomplete dictionary, that is, over all
th iteration, find the Gabor logon over the whole overcomplete dictionary, that is, over all  , that has the largest inner product with the residue time-frequency surface,
, that has the largest inner product with the residue time-frequency surface, 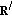
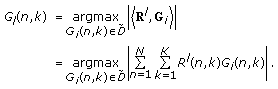
 th step,
th step, 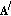 , as
, as 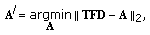
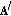 , from the residue to compute the new residue time-frequency distribution at the
, from the residue to compute the new residue time-frequency distribution at the 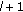 th iteration
th iteration 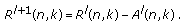
 by 1, set
by 1, set  .
. and the approximation at the lth iteration is below a predetermined threshold, that is,
and the approximation at the lth iteration is below a predetermined threshold, that is,