- Research Article
- Open access
- Published:
Underwater Broadband Source Localization Based on Modal Filtering and Features Extraction
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 304103 (2010)
Abstract
Passive source localization is a crucial issue in underwater acoustics. In this paper, we focus on shallow water environment (0 to 400 m) and broadband Ultra-Low Frequency acoustic sources (1 to 100 Hz). In this configuration and at a long range, the acoustic propagation can be described by normal mode theory. The propagating signal breaks up into a series of depth-dependent modes. These modes carry information about the source position. Mode excitation factors and mode phases analysis allow, respectively, localization in depth and distance. We propose two different approaches to achieve the localization: multidimensional approach (using a horizontal array of hydrophones) based on frequency-wavenumber transform ( method) and monodimensional approach (using a single hydrophone) based on adapted spectral representation (
method) and monodimensional approach (using a single hydrophone) based on adapted spectral representation ( method). For both approaches, we propose first complete tools for modal filtering, and then depth and distance estimators. We show that adding mode sign and source spectrum informations improves considerably the localization performance in depth. The reference acoustic field needed for depth localization is simulated with the new realistic propagation modelMoctesuma. The feasibility of both approaches,
method). For both approaches, we propose first complete tools for modal filtering, and then depth and distance estimators. We show that adding mode sign and source spectrum informations improves considerably the localization performance in depth. The reference acoustic field needed for depth localization is simulated with the new realistic propagation modelMoctesuma. The feasibility of both approaches,  and
and  , are validated on data simulated in shallow water for different configurations. The performance of localization, in depth and distance, is very satisfactory.
, are validated on data simulated in shallow water for different configurations. The performance of localization, in depth and distance, is very satisfactory.
1. Introduction
Passive source localization in shallow water has attracted much attention for many years in underwater acoustics. In this environment and for Ultra-Low Frequency waves ( to
to  Hz, denoted further ULF) classical beamforming techniques are inappropriate because they do not consider multipath propagation phenomena and ocean acoustic channel complexity. Indeed, ULF acoustic propagation in shallow water waveguides is classically based on normal mode theory [1]. ULF band is very attractive for detection, localization, and geoacoustical parameter estimation purposes, because propagating acoustic waves are almost not affected by absorption and thus can propagate at very long ranges. In this context, mainly two approaches are used: Matched-Field Processing (denoted MFP) [2, 3] and Matched-Mode Processing (denoted MMP) [4–6]. The comparative study of both approaches is given in [7]. Matched-Mode approach can be considered as MFP combined with modal decomposition. The main difference is that MFP operates in receiver space and MMP in mode space. Both methods require a reference acoustic field (replica field) to be compared, generally by correlation techniques (building and maximizing an objective function), with the real acoustic field recorded on receiver(s). Another alternative to perform source localization is to use time reversal [8] which can be seen as a broadband coherent MFP. Some experiments have been performed showing the feasibility of the method [9]. The main drawback of the method is that a numerical backpropagation has to be computed which needs a good knowledge of the environment. As MMP is less sensitive to environmental mismatches than MFP and Time Reversal methods, this technique is more interesting for practical applications, and thus is used in our approach to estimate the source depth. The access to modes not only allows estimation of mode excitation factors for depth localization, but also gives the possibility to analyze mode phase to extract information about the source distance. As a result, in this paper depth estimation is performed using MMP on the mode excitation factors and distance estimation is achieved by mode phase analysis.
Hz, denoted further ULF) classical beamforming techniques are inappropriate because they do not consider multipath propagation phenomena and ocean acoustic channel complexity. Indeed, ULF acoustic propagation in shallow water waveguides is classically based on normal mode theory [1]. ULF band is very attractive for detection, localization, and geoacoustical parameter estimation purposes, because propagating acoustic waves are almost not affected by absorption and thus can propagate at very long ranges. In this context, mainly two approaches are used: Matched-Field Processing (denoted MFP) [2, 3] and Matched-Mode Processing (denoted MMP) [4–6]. The comparative study of both approaches is given in [7]. Matched-Mode approach can be considered as MFP combined with modal decomposition. The main difference is that MFP operates in receiver space and MMP in mode space. Both methods require a reference acoustic field (replica field) to be compared, generally by correlation techniques (building and maximizing an objective function), with the real acoustic field recorded on receiver(s). Another alternative to perform source localization is to use time reversal [8] which can be seen as a broadband coherent MFP. Some experiments have been performed showing the feasibility of the method [9]. The main drawback of the method is that a numerical backpropagation has to be computed which needs a good knowledge of the environment. As MMP is less sensitive to environmental mismatches than MFP and Time Reversal methods, this technique is more interesting for practical applications, and thus is used in our approach to estimate the source depth. The access to modes not only allows estimation of mode excitation factors for depth localization, but also gives the possibility to analyze mode phase to extract information about the source distance. As a result, in this paper depth estimation is performed using MMP on the mode excitation factors and distance estimation is achieved by mode phase analysis.
Consequently, the main issue to perform underwater localization for ULF sources in shallow water is to develop signal processing methods to accomplish modal filtering. These methods should be based on physics of wave propagation in waveguides, to be adapted to signals propagating in shallow water environment. In this context, we propose two complementary techniques to localize broadband impulsive source in depth and distance. The first method based on frequency-wavenumber transform and denoted  is a multidimensional approach based on array processing. The second method based on adapted Fourier transform and denoted
is a multidimensional approach based on array processing. The second method based on adapted Fourier transform and denoted  is a monodimensional technique used on a single hydrophone.
is a monodimensional technique used on a single hydrophone.
Traditionally, matched-mode localization was applied on vertical line arrays (VLAs), and mode excitation factors were extracted by a spatial integration of pressure field. As proposed in [10, 11], we record the signal (represented in the space: radial distance  and time
and time  ) on a horizontal line array (HLA), as it is generally more practical in real applications (towing possibility, faster deployment, and stability). In this configuration, modes can be filtered in the frequency-wavenumber plane (
) on a horizontal line array (HLA), as it is generally more practical in real applications (towing possibility, faster deployment, and stability). In this configuration, modes can be filtered in the frequency-wavenumber plane ( ), which is a two-dimensional Fourier transform of radial distance-time section (signal
), which is a two-dimensional Fourier transform of radial distance-time section (signal  ).
).
For the mono-dimensional approach, modes cannot be filtered by conventional modal filtering techniques. As modes have nonstationary properties, the only way to filter modes is to integrate modal time-frequency characteristics [12] into modal filtering. The main idea is to deform a signal in such way that nonlinearities in the time-frequency plane become linear (according to the frequency domain). Consequently, the signal becomes stationary and classical filtering tools can be used to filter modes. Hereby, modal filtering in mono-dimensional configuration is done in an adapted frequency domain (Pekeris Fourier transform). The classical and adapted frequency domains are related by the unitary equivalence formalism [13].
After a brief presentation of modal propagation theory, we give a short description of the simulator Moctesuma-2006, which is used for simulation of acoustic replica fields and acoustic parameter computation. Then, we present details about the experimental configuration. Next, we describe mode filtering methods in the mono- and multidimensional cases to finally present estimators used for depth and distance localization. Finally, results of distance and depth localization for mono and multidimensional method are presented on simulated data.
2. Modal Propagation and Modes
Acoustic propagation of Ultra-Low Frequency waves in shallow water waveguide can be modeled by normal mode theory. Propagating signal at long range is composed of dispersive modes. These modes are analyzed for depth (matched-mode processing) and distance (mode phase processing) localization.
To demonstrate very succinctly the idea of localization using modes, we introduce the simplest model of oceanic waveguide—the perfect waveguide. Even if this model is a simplification of real complex waveguides, it reflects the most important waveguide phenomena: modal decomposition of the propagated signal.
The perfect waveguide model is made of a homogeneous layer of water between perfectly reflecting boundaries (a pressure release surface and a rigid sea bottom). The water layer is characterized by depth  , velocity
, velocity  and density
and density  . We consider an omnidirectional point source located at depth
. We consider an omnidirectional point source located at depth  and at distance
and at distance  radiating a signal
radiating a signal  . The acoustic pressure field
. The acoustic pressure field  received at a reception point of coordinates
received at a reception point of coordinates  , where
, where  and
and  are, respectively, horizontal distance and depth, can be expressed by
are, respectively, horizontal distance and depth, can be expressed by

where  is the time,
is the time,  is the frequency, and
is the frequency, and  satisfies the general Helmholtz equation.
satisfies the general Helmholtz equation.
Using variable separation (in depth and in range) and boundaries conditions [1], the pressure  at long range becomes a sum of modes
at long range becomes a sum of modes

with  a constant,
a constant,  the source spectrum,
the source spectrum,  the modal function of mode
the modal function of mode  , and
, and  the horizontal spatial frequency of mode
the horizontal spatial frequency of mode  . The spatial frequency
. The spatial frequency  is defined by
is defined by  and it corresponds to the classical wavenumber divided by
and it corresponds to the classical wavenumber divided by  In the following, for the sake of simplicity, we will call
In the following, for the sake of simplicity, we will call  the wavenumber with its horizontal and vertical components
the wavenumber with its horizontal and vertical components  and
and  (instead of spatial frequency). The mode wavenumber spectrum is discrete and each mode is associated with an unique wavenumber. The amplitude
(instead of spatial frequency). The mode wavenumber spectrum is discrete and each mode is associated with an unique wavenumber. The amplitude  is a function of the source depth
is a function of the source depth  :
:

with  .
.
This short theoretical introduction of normal mode theory made on the example of perfect waveguide exposes the principle used for source depth estimation; mode amplitudes depend on source depth  by the factor
by the factor  .
.
Then, let us demonstrate very shortly the principle of mode phase processing for distance estimation. Modes contain, besides depth information, also distance information about the source. This information is contained in mode phase. The phase of mode  at frequency
at frequency  is defined by
is defined by

where
-
(i)
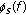 is the phase of the source at frequency
is the phase of the source at frequency 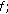
-
(ii)
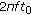 is a phase factor due to time delay
is a phase factor due to time delay 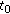 of the recorded signal;
of the recorded signal; -
(iii)
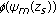 depends on the modal function sign at the source depth
depends on the modal function sign at the source depth 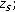 it is
it is  if
if 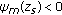 and
and  if
if 
-
(iv)
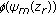 depends on the modal function sign at the receiver depth
depends on the modal function sign at the receiver depth 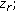
-
(v)
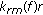 is a phase factor at frequency
is a phase factor at frequency 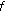 linked to the propagation distance
linked to the propagation distance  between source and receiver.
between source and receiver.
As one can notice, modal decomposition is a very useful theory for acoustic propagation in oceanic waveguide. Indeed, MMP uses this decomposition to perform localization [14].
In this section we demonstrated that by having access to modes, and more precisely to their excitation factors and phases, it is possible to localize source in depth and in distance.
Moctesuma-
To perform the depth estimation using MMP, we need an acoustic model to generate replica fields. Several classical underwater acoustic propagation models exist in the literature and are used according to the seabed depth, the source range, and the frequency band. Models are based on different theories: ray theory, parabolic equation modeling, normal mode models, and spectral integral models [1]. Among the different models we choose the numerical model Moctesuma-2006—a realistic underwater acoustic propagation simulator developed by Thales Underwater Systems [15]. For the sake of simplicity Moctesuma-2006 will be called further Moctesuma. This model, based on normal mode theory, simulates an underwater acoustic propagation for range-dependent environments. It is well adapted to transient broadband ULF signals for shallow and deep water environments. Moreover, we choose Moctesuma as it provides the acoustic parameters of the environment (wavenumbers) and the full acoustic field (time-series) [16].
The transmitted transient signal is first split into narrow subbands signals through a set of bandpass filters. Each subband is associated with a central frequency for which acoustic modes are fully computed. For each mode in each subband, propagation consists in delaying the original signal. The summation is performed in the time domain, so the signal causality is necessarily satisfied. Moctesuma considers different acoustic signal phenomena such as penetration, elasticity, multiple interactions inside multilayered sea bottoms and water. The time and space structure of waves is analyzed beyond simple wavefronts and Doppler effect (moving source and/or receiver).
A set of parameters is necessary to make a simulation with Moctesuma. The first parameter group concerns a description of the environment. As it is a range-dependent model, parameters are given for each environment sector. User has to provide following environmental parameters: sea state, temperature, sound speed profile, seabed type (or precise seabed structure). The second parameter group concerns the input signal and the experiment configuration (coordinates, depths, speeds and caps of the source and the antenna, antenna's length, and sensors' number).
In our analysis, we use Moctesuma to simulate the reference acoustic field (in the MMP) and to access the acoustic parameters of the environment such as horizontal wavenumbers, group velocities, and mode excitation factors signs.
3. Experimental Configuration
3.1. Environment
The analysis presented in this paper is done in a simulated shallow water environment located in the Mediterranean Sea during a summer period. The environment is range independent with a water depth of  m. The sound speed profile of the water column (Figure 1) is characterized by a strong negative gradient of approximately
m. The sound speed profile of the water column (Figure 1) is characterized by a strong negative gradient of approximately  m/s. The highest gradient is located in the first half of the water column. The seabed parameters are presented in Figure 2. Modal functions no.
m/s. The highest gradient is located in the first half of the water column. The seabed parameters are presented in Figure 2. Modal functions no.  to
to  of the studied environment are presented in Figure 3.
of the studied environment are presented in Figure 3.
3.2. Signal Sources and Reception Configurations
In this paper we consider two impulsive broadband sources in the ULF band: the first one ULF lasts several tens of milliseconds and has a flat spectrum; the second source ULF
lasts several tens of milliseconds and has a flat spectrum; the second source ULF lasts several hundreds of milliseconds and is made of four band signals ("
lasts several hundreds of milliseconds and is made of four band signals (" hills" spectrum). Both signals are presented in temporal and spectral domains in Figure 4.
hills" spectrum). Both signals are presented in temporal and spectral domains in Figure 4.
The source ULF is used to validate the methods in a simple case. For a more complex situation source ULF-2 is then used in Section 6.3.
is used to validate the methods in a simple case. For a more complex situation source ULF-2 is then used in Section 6.3.
Signals radiated by source are recorded on a horizontal line array (HLA) after acoustic propagation. The HLA is  m long and is composed of
m long and is composed of  omnidirectional equispaced hydrophones (separated by
omnidirectional equispaced hydrophones (separated by  m). The sampling frequency is
m). The sampling frequency is  Hz.
Hz.
The experimental configuration is given on Figure 5. Three different source depths  are studied:
are studied:  m,
m,  m, and
m, and  m. The horizontal distance between the source and the first sensor of HLA is equal to
m. The horizontal distance between the source and the first sensor of HLA is equal to  km. The HLA is located on the sea bottom (
km. The HLA is located on the sea bottom ( ). The HLA can be located at any depth, but this information has to be known. In our simulations the source and the HLA are motionless.
). The HLA can be located at any depth, but this information has to be known. In our simulations the source and the HLA are motionless.
3.3. Data
Moctesuma simulator provides a section of the pressure recorded on the HLA  denoted signal
denoted signal  for the sake of simplicity in the following. It is a sampling of the pressure field in radial distance
for the sake of simplicity in the following. It is a sampling of the pressure field in radial distance  and in time
and in time  . The size of the data is defined by
. The size of the data is defined by
-
(i)
number of hydrophones (traces)
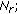
-
(ii)
duration and frequency sampling of the recording (number of samples
 ).
).
The "real data" is obtained by adding a white bi-dimensional (in time and in space) Gaussian noise to the simulated data. Several signal-to-noise ratios (SNRs) are considered.
4. Filtering Methods
In this paper, source localization in depth and distance is performed either by multi-dimensional or by mono-dimensional approach. The first one will be called  approach (as the method operates in the frequency-wavenumber domain
approach (as the method operates in the frequency-wavenumber domain  ) and the second one
) and the second one  approach (as the method is based on adapted Fourier transform). They both achieve modal filtering which is described in this section.
approach (as the method is based on adapted Fourier transform). They both achieve modal filtering which is described in this section.
For the first approach, in the frequency-wavenumber plane ( ) modes are separated and thus can be filtered. In the second approach, which is theoretically more difficult as we have a single hydrophone, modes are not easily separable and thus, cannot be filtered using classical signal representations such as Fourier transform or time-frequency representation. As proposed in [12, 17], we use an adapted frequency representation in which modes are separable and consequently can be filtered.
) modes are separated and thus can be filtered. In the second approach, which is theoretically more difficult as we have a single hydrophone, modes are not easily separable and thus, cannot be filtered using classical signal representations such as Fourier transform or time-frequency representation. As proposed in [12, 17], we use an adapted frequency representation in which modes are separable and consequently can be filtered.
4.1. Multi-Dimensional Approach
In the multi-dimensional case, the radial distance-time section  is represented in the frequency-wavenumber plane
is represented in the frequency-wavenumber plane  . The transformation, called
. The transformation, called  transform and denoted by
transform and denoted by  , is linked to
, is linked to  via a two-dimensional Fourier transform (in radial distance
via a two-dimensional Fourier transform (in radial distance  and in time
and in time  ). The
). The  transform of the signal
transform of the signal  is defined by
is defined by

To improve dynamics of modal representation and avoid spatial aliasing in the  plane, a
plane, a  velocity correction on the section
velocity correction on the section  is applied before calculating
is applied before calculating  transform [11] (classical preprocessing technique used in array processing). This operation consists in applying to every trace of the section a time shift, so that the direct wave (traveling with speed
transform [11] (classical preprocessing technique used in array processing). This operation consists in applying to every trace of the section a time shift, so that the direct wave (traveling with speed  , equal to
, equal to  in the perfect waveguide) arrives at every sensor at the same time (giving an apparent infinite velocity). Let us denote
in the perfect waveguide) arrives at every sensor at the same time (giving an apparent infinite velocity). Let us denote  the
the  representation of the section
representation of the section  . Then,
. Then,  representation of the section after velocity correction
representation of the section after velocity correction  is
is

The consequence of this processing is a shifting of every point in the  plane in such way that the spatial aliasing is canceled and the representation space of modes is much larger (greater dynamics, simpler filtering).
plane in such way that the spatial aliasing is canceled and the representation space of modes is much larger (greater dynamics, simpler filtering).
If we consider a white broadband source radiating a transient signal in a perfect waveguide, the  transform of the pressure signal (see (2)) received on the HLA, at long range, can be approximated by
transform of the pressure signal (see (2)) received on the HLA, at long range, can be approximated by

with  a frequency dependent constant related to the source spectrum.
a frequency dependent constant related to the source spectrum.
The theoretical modal signal energy is located on the mode dispersion curves  (the form of the mode dispersion curves is given in Figure 6). As one can notice, for each frequency the wavenumber spectrum is discrete. The
(the form of the mode dispersion curves is given in Figure 6). As one can notice, for each frequency the wavenumber spectrum is discrete. The  representations of two data sets are given in Figure 7. The first plot shows a simulation done with signal ULF-1 (flat spectrum) at depth
representations of two data sets are given in Figure 7. The first plot shows a simulation done with signal ULF-1 (flat spectrum) at depth  m. The energy is spread across all the frequency band. The second plot presents a simulation with signal ULF-2 ("
m. The energy is spread across all the frequency band. The second plot presents a simulation with signal ULF-2 (" hills" spectrum) at depth
hills" spectrum) at depth  m. The
m. The  representation reflects exactly the spectrum of the source signal (see Figure 4).
representation reflects exactly the spectrum of the source signal (see Figure 4).
Moctesuma's dispersion curves no. 1 to 10 in frequency-wavenumber domain afterVref velocity correction (in plot, the mode number increases from (b) to (a)). Wavenumbers in (a) correspond to all propagating modes (water and seabed), and these in (b) plot correspond only to modes propagating in the water column.
As the HLA is located at a known depth, values of the factors  are known. For HLA located on the sea bottom
are known. For HLA located on the sea bottom  and expression (7) can be rewritten as
and expression (7) can be rewritten as

The amplitude of the  transform for each curve (dispersive mode) depends only on the mode excitation factor modulus. We use these curves to estimate the excitation factor modulus of each mode. For a perfect waveguide model there is no frequency dependence for modal functions, which is the case in reality. Therefore, excitation factor of mode
transform for each curve (dispersive mode) depends only on the mode excitation factor modulus. We use these curves to estimate the excitation factor modulus of each mode. For a perfect waveguide model there is no frequency dependence for modal functions, which is the case in reality. Therefore, excitation factor of mode  is estimated as the mean value across the frequency domain. Moreover, mode excitation factors at the bottom interface are not exactly equal to
is estimated as the mean value across the frequency domain. Moreover, mode excitation factors at the bottom interface are not exactly equal to  and will slightly modify the estimation of the mode amplitude at the source depth. This phenomenon does not affect the result as the same methodology is applied for the replica data.
and will slightly modify the estimation of the mode amplitude at the source depth. This phenomenon does not affect the result as the same methodology is applied for the replica data.
Mask Construction
Once  representation of the signal is calculated, a mask filtering has to be applied to filter modes. The mask is a binary image (with the same size as the
representation of the signal is calculated, a mask filtering has to be applied to filter modes. The mask is a binary image (with the same size as the  transform) and is used to extract a mode by a simple multiplication in the
transform) and is used to extract a mode by a simple multiplication in the  domain. The mask built for each mode should "cover" the region occupied by this mode in the
domain. The mask built for each mode should "cover" the region occupied by this mode in the  plane.
plane.
An initial mask of mode  is created using its wavenumbers. These can be computed theoretically by a propagation model if the environmental parameters are known. In our case they are given by Moctesuma (see Figure 6). Then, the mask of mode
is created using its wavenumbers. These can be computed theoretically by a propagation model if the environmental parameters are known. In our case they are given by Moctesuma (see Figure 6). Then, the mask of mode  is dilated independently in both domains (frequency and wavenumber) with the dilation parameter
is dilated independently in both domains (frequency and wavenumber) with the dilation parameter  according to the following formula:
according to the following formula:

where  and
and  denote, respectively, dilation sizes in wavenumber (
denote, respectively, dilation sizes in wavenumber ( ) and frequency (
) and frequency ( ) domains, and
) domains, and  and
and  denote, respectively, the sampling period in wavenumber and frequency domains. The first parameter
denote, respectively, the sampling period in wavenumber and frequency domains. The first parameter  determines the distances between successive masks (depends on mode number
determines the distances between successive masks (depends on mode number  ) and the second parameter
) and the second parameter  defines the distance of the mask for mode
defines the distance of the mask for mode  to the frequency
to the frequency  Hz. This definition of dilation parameters makes the mask width in the frequency dimension adapted to the frequency (narrower masks at high frequencies for lower number modes and larger masks at lower frequencies for higher number modes). The dilation process is restricted by limitation that the masks for different modes must not overlap. These masks allow an efficient filtering even for higher modes which are usually more difficult to filter.
Hz. This definition of dilation parameters makes the mask width in the frequency dimension adapted to the frequency (narrower masks at high frequencies for lower number modes and larger masks at lower frequencies for higher number modes). The dilation process is restricted by limitation that the masks for different modes must not overlap. These masks allow an efficient filtering even for higher modes which are usually more difficult to filter.
The simulated environment has to be as close as possible to the real environment to achieve a good filtering of modes. Moreover, it is necessary to dilate the previous theoretical mask for two reasons:
-
(i)
the limited HLA length-mode energy spreads around dispersion curves in the
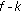 plane;
plane; -
(ii)
the mismatch between real and simulated environments [11].
A total set of masks for the studied environment is given in Figure 8. This set contains  masks which corresponds to the total number of propagating modes in this environment. An example of the mask adapted to mode no.
masks which corresponds to the total number of propagating modes in this environment. An example of the mask adapted to mode no.  is given in Figure 9. The mask of mode no.
is given in Figure 9. The mask of mode no.  is built starting from its dispersion curve (see Figure 6,
is built starting from its dispersion curve (see Figure 6,  trace counting from right to left) and then dilated according to (9).
trace counting from right to left) and then dilated according to (9).
Set of binary masks in the f-k domain built from dispersion curves given in Figure 6 by bi-dimensional dilatation process. The set is complete for the studied environment.
The energy spectrum of data in Figure 7(a) is shown in Figure 10. For each mode the energy is calculated as a mean of the  region where this mode is present (after mask filtering).
region where this mode is present (after mask filtering).
In Figure 11 we present the result of the mode filtering for modes nos.  ,
,  (mode with very low energy), and
(mode with very low energy), and  (the mode with the highest energy).
(the mode with the highest energy).
Modes nos. 1, 4 and 6 extracted from F-K representation given in Figure 7(a) by mask filtering.
4.2. Monodimensional Approach
In the mono-dimensional configuration, classical signal representations such as Fourier transform or short-time Fourier transform are not suited for description of a signal that can be decomposed in a sum of dispersive modes (nonstationary and nonlinear time-frequency patterns). Therefore, these techniques cannot correctly represent the signal having modal structures (see Figures 12(a) and 13(a)). This signal processing problem has attracted much interest for the last decades [13, 18, 19]. In this paper we based our monosensor approach on works [12, 17, 20]. The idea is to find a representation well adapted for modal signal structure to achieve modal filtering. The best way is to take into account the physics of oceanic waveguide propagation and build a representation adapted to the signal structure in the same way as Fourier transform is adapted to a monochromatic signal. Here, we discuss only an adapted frequency representation  . However, on the same rule an adapted time-frequency representation can be constructed and used [12, 17].
. However, on the same rule an adapted time-frequency representation can be constructed and used [12, 17].
Classical Fourier spectrum and adapted Fourier spectrum of a signal recorded on a single hydrophone (the same as in Figure 12).
The adapted processing tools are based on the combination between acoustic wave propagation (waveguide propagation law) and signal processing theory (unitary equivalence). Building of the adapted frequency representation is based primary on definition of the unitary operator of transformation adapted to guided waves. This unitary operator is linked to the dispersion law  , where
, where  is the instantaneous frequency and
is the instantaneous frequency and  is the time. For a perfect waveguide model and for each mode
is the time. For a perfect waveguide model and for each mode  the dispersion law is defined by
the dispersion law is defined by

where  is the sound speed in water,
is the sound speed in water,  is the waveguide depth,
is the waveguide depth,  is the time, and
is the time, and  is the distance. This relation defines temporal domain of group delay
is the distance. This relation defines temporal domain of group delay  where
where  is arrival time of the wavefront.
is arrival time of the wavefront.
Starting from the dispersive relation given in 10, the instantaneous frequency  is the derivative of the instantaneous phase
is the derivative of the instantaneous phase  :
:

with  the cut-off frequency of mode
the cut-off frequency of mode  defined by
defined by

 is called the general dispersive function and is defined as follows:
is called the general dispersive function and is defined as follows:

As a result, the pressure signal of the perfect waveguide model is defined by

with  the envelope evolution of mode
the envelope evolution of mode  The unitary operator of transformation should transform nonlinear mode structures in linear ones (in time-frequency domain), and thus allow the use of classical Fourier filtering techniques. In construction of such representation, the unitary equivalence formalism is used [13]. One of the unitary operators is a warping operator
The unitary operator of transformation should transform nonlinear mode structures in linear ones (in time-frequency domain), and thus allow the use of classical Fourier filtering techniques. In construction of such representation, the unitary equivalence formalism is used [13]. One of the unitary operators is a warping operator  (applied to a signal
(applied to a signal  ) defined as follows:
) defined as follows:

The function  has to be derivable and bi-univocal, and function
has to be derivable and bi-univocal, and function  has to exist. The operator
has to exist. The operator  is applied to the signal in order that
is applied to the signal in order that  becomes a sum of linear structures
becomes a sum of linear structures

To do so, we deduce from (16), the deformation function  defined on
defined on 

Finally, the unitary operator of transformation adapted to a perfect waveguide is

Note that this tool is reversible, so one can go back to the initial representation space (time or frequency).
In this short presentation of adapted transformation for the perfect waveguide we demonstrated the principal idea of this technique which consists in transformation of modes into linear structures. In our work we use a method adapted to Pekeris waveguide model, as it is a more complex model (closer to reality) taking into account the interaction with the sea bottom (described in details in [12]).
As the non-linear time-frequency signal structures become linear after this transformation, the signal becomes stationary (see Figures 12(b) and 13(b)). In this case, one can use classical frequency filtering tools to filter modes. The modal filtering is then done in the adapted frequency domain (Pekeris frequency) by a simple bandpass filtering defined by the user.
5. Estimators
In Section 4 we demonstrated how extracting modes from the recorded signal by multi and mono-dimensional approaches. In this section we discuss depth and distance estimators based on modal processing. For depth estimation, we use a matched-mode technique, and for distance estimation our approach is based on mode phase analysis. For both approaches,  and
and  , we use the same estimators for localization in depth and distance. The only difference is the representation space of modal filtering: frequency-wavenumber for
, we use the same estimators for localization in depth and distance. The only difference is the representation space of modal filtering: frequency-wavenumber for  method and adapted Fourier spectrum for
method and adapted Fourier spectrum for  method.
method.
5.1. Range Estimation
The range estimation is combined with the mode sign estimation; therefore we call the estimator sign-distance estimator. The estimator applied only on the real data is based on mode phase analysis and calculates a cost function  based on two mode phases (
based on two mode phases ( and
and  , where
, where  ) extracted from the data. Modes are not necessarily consecutive; however their numbers and associated wavenumbers (calculated by Moctesuma) have to be known.
) extracted from the data. Modes are not necessarily consecutive; however their numbers and associated wavenumbers (calculated by Moctesuma) have to be known.
The sign-distance estimator is originally based on a work published in [20]. We present this estimator very succinctly, more details can be found in [21]. The principle is based on the definition of mode phase given in (4). To suppress the unknown parameters in this equation, the initial estimator  uses the difference between two mode phases:
uses the difference between two mode phases:

with
-
(i)
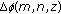 being difference between two mode phases at depth
being difference between two mode phases at depth  ; the values of this parameter are defined by (for details see Table 1):
; the values of this parameter are defined by (for details see Table 1):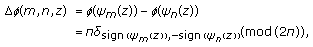 (20)
(20) -
(ii)
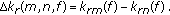

The estimation is done in sequential way; that is, superior mode signs (of order  ) are estimated using inferior mode signs (of order
) are estimated using inferior mode signs (of order  ). The starting point is the absolute mode sign of mode no.
). The starting point is the absolute mode sign of mode no.  which is always positive:
which is always positive:  For example to estimate the sign of mode
For example to estimate the sign of mode  one can use in theory modes
one can use in theory modes  As the frequency band shared by two modes (
As the frequency band shared by two modes ( and
and  ) has to be maximized for the estimation performance, we propose the following rule to choose inferior mode number (
) has to be maximized for the estimation performance, we propose the following rule to choose inferior mode number ( ) for estimation of superior sign mode number (
) for estimation of superior sign mode number ( ):
):

The sign of  is known as the depth
is known as the depth  of HLA is known (in our case it is
of HLA is known (in our case it is  ). To estimate mode signs for real data, for each frequency
). To estimate mode signs for real data, for each frequency  the quantity
the quantity  is measured, and then we calculate the cost function
is measured, and then we calculate the cost function  defined as
defined as

where  is the distance function defined as
is the distance function defined as

with  defined on a basic interval
defined on a basic interval  . The sign-distance estimator is found by the minimization of the cost function
. The sign-distance estimator is found by the minimization of the cost function  :
:

where  and
and

The sign-distance estimator is calculated for  possible values of
possible values of  :
:  and
and  . By minimizing
. By minimizing  , we find the searched value of
, we find the searched value of  (using (25), the relative sign between modes
(using (25), the relative sign between modes  and
and  is estimated) and also the distance. As we know the absolute sign
is estimated) and also the distance. As we know the absolute sign  of inferior mode
of inferior mode  (known or estimated in previous step of estimation) and the estimated value of the pass function
(known or estimated in previous step of estimation) and the estimated value of the pass function  betwen modes
betwen modes  and
and  , we can find the absolute sign of mode
, we can find the absolute sign of mode 

 . The rule of mode sign estimation is given in Table 2.
. The rule of mode sign estimation is given in Table 2.

 depends on the absolute sign of mode
depends on the absolute sign of mode 
 and the pass function
and the pass function  (where
(where  ).
).The mode sign estimation for  takes at least
takes at least  steps as the first mode sign is always positive and as the estimator works sequentially on mode couples.
steps as the first mode sign is always positive and as the estimator works sequentially on mode couples.
5.2. Depth Estimation
Source depth estimation is based on Matched-Mode Processing. The principle of MMP is to compare modes in terms of excitation factors extracted from the real data with those extracted from the replica fields. The modeled acoustic field (replica) is simulated with Moctesuma. The depth estimator is based on a correlation which measures a distance between mode excitation factors estimated from real and from simulated data (for a set of investigated depths). The depth for which this correlation reaches maximum (the best matching) is chosen as the estimated source depth.
The mode excitation factors are extracted by  or
or  approach on real and replica data in the same manner. They are positive as they are extracted from positive value spaces (
approach on real and replica data in the same manner. They are positive as they are extracted from positive value spaces ( transform or modulus of the adapted Fourier transform). Their signs are then obtained using the sign-distance estimator presented in the previous section. The mode signs are estimated only for real data. For the reference data, as the simulations are done for a set of determined source depths, mode signs are known. The combination of mode excitation factors with mode signs allows canceling secondary peaks in the correlation function. These peaks are due to "mirror solutions" of modal functions for some depths when considering only mode excitation factor modulus (see Figure 14). Therefore, adding mode sign information to mode excitation factor modulus improves significantly the performance of depth localization (shown on examples in Section 6).
transform or modulus of the adapted Fourier transform). Their signs are then obtained using the sign-distance estimator presented in the previous section. The mode signs are estimated only for real data. For the reference data, as the simulations are done for a set of determined source depths, mode signs are known. The combination of mode excitation factors with mode signs allows canceling secondary peaks in the correlation function. These peaks are due to "mirror solutions" of modal functions for some depths when considering only mode excitation factor modulus (see Figure 14). Therefore, adding mode sign information to mode excitation factor modulus improves significantly the performance of depth localization (shown on examples in Section 6).
The localization performance is strongly dependent of the matching accuracy between real and simulated acoustic fields. Study of the influence of environmental and system effects on the localization performance is presented in [11, 22]. The dilation used to build masks in the  plane makes the method more robust against these errors.
plane makes the method more robust against these errors.
To compare mode excitation factors extracted from real and simulated data, a normalization based on the closure relationship is applied:

where  is an excitation factor of mode
is an excitation factor of mode  . Then, the comparison between mode excitation factors extracted from the real data
. Then, the comparison between mode excitation factors extracted from the real data  and replica data
and replica data  is made using the contrast function
is made using the contrast function  :
:

where  is the number of analyzed modes
is the number of analyzed modes

The maximum of  indicates the estimated depth of the source.
indicates the estimated depth of the source.
In matched-mode localization, modes for which the function  defined by (27) is calculated are theoretically unrestricted. However, in case of ULF localization, only the first modes are used. The upper mode number limit is given by the environment and existence of cut-off frequencies as the methods presented in this paper are based on broadband signal processing. In our analysis the number of used modes is between
defined by (27) is calculated are theoretically unrestricted. However, in case of ULF localization, only the first modes are used. The upper mode number limit is given by the environment and existence of cut-off frequencies as the methods presented in this paper are based on broadband signal processing. In our analysis the number of used modes is between  and
and  .
.
Theoretical performances of depth localization for the studied environment and for all source depths are presented in Figure 14 (each vertical line corresponds to a contrast function  ). The figure presents two plots: for the method without mode signs (a) and for the method with mode signs (b). The result is obtained by the application of (27) to mode excitation factors directly taken from Moctesuma simulations. For the method without mode signs, one can notice the existence of "mirror solutions" which is a line of secondary peaks intersecting with the primary peaks line indicating the true source positions. That line does not exist for the method with mode signs, as the "mirror solutions" are cancelled by adding mode signs to mode excitation factor modulus. In such way, one can remove the localization ambiguity, which is problematic especially in low signal-to-noise conditions.
). The figure presents two plots: for the method without mode signs (a) and for the method with mode signs (b). The result is obtained by the application of (27) to mode excitation factors directly taken from Moctesuma simulations. For the method without mode signs, one can notice the existence of "mirror solutions" which is a line of secondary peaks intersecting with the primary peaks line indicating the true source positions. That line does not exist for the method with mode signs, as the "mirror solutions" are cancelled by adding mode signs to mode excitation factor modulus. In such way, one can remove the localization ambiguity, which is problematic especially in low signal-to-noise conditions.
5.3. Source Spectrum Estimation
To perform matched-mode localization, knowledge (at least partial) of quantities such as geoacoustical parameters of the environment and spectral characteristics of the source is crucial. This results from the fact that the simulated acoustic field should be simulated in geoacoustical conditions similar (as much as possible) to the real conditions existing in the location of interest. In general, environmental parameters can be estimated using inversion methods [23, 24]. Unluckily, in passive approach the knowledge of the source spectrum remains notwithstanding problematic. As the influence of the source spectrum is relevant (see (2) and (7)), we propose an estimator of source spectrum based on the analysis of the first mode (most horizontal), as this mode is always excited. The property of distinct attenuation of signal frequencies (growing non linearly with the frequency) is taken into account by the estimator in order to improve estimation quality. The proposed estimator can be formulated as follows:

where  is the estimated source spectrum,
is the estimated source spectrum,  is a spectral factor correcting the signal attenuation over frequency,
is a spectral factor correcting the signal attenuation over frequency,  is a number of hydrophones, and
is a number of hydrophones, and  is the spectrum of the first mode on hydrophone
is the spectrum of the first mode on hydrophone  estimated from the
estimated from the  plane. For better performance the correction factor
plane. For better performance the correction factor  can be measured in the field (by recording a known broadband signal at some distance). As we do not operate on real field data, to calculate
can be measured in the field (by recording a known broadband signal at some distance). As we do not operate on real field data, to calculate  we use theoretical values of spectral attenuation (for frequency range of interest).
we use theoretical values of spectral attenuation (for frequency range of interest).
6. Localization
We present some examples of source localization using methods described in Sections 4 and 5. First, examples of localization in distance and in depth are presented using a single hydrophone, and then using a horizontal hydrophone array (HLA). Moreover, we show the interest of mode signs and source spectrum estimations in case of depth localization by  and
and  approaches. Due to limited paper's length, we do not expose here the study of the robustness of the methods against noise. These considerations have been studied in [11, 25]. We give only some most important conclusions. The simulations on source depth estimation demonstrate that to obtain the primary peak-to-secondary peak ratio of
approaches. Due to limited paper's length, we do not expose here the study of the robustness of the methods against noise. These considerations have been studied in [11, 25]. We give only some most important conclusions. The simulations on source depth estimation demonstrate that to obtain the primary peak-to-secondary peak ratio of  dB the signal-to-noise ratio has to be superior to
dB the signal-to-noise ratio has to be superior to  dB for
dB for  method and
method and  dB for
dB for  method. The impact of noise on source range estimation seems to be more relevant. These considerations concern white (in time and in space) gaussian model of local (non propagating) noise.
method. The impact of noise on source range estimation seems to be more relevant. These considerations concern white (in time and in space) gaussian model of local (non propagating) noise.
6.1. One Hydrophone
The objective of this section is to show performance of  localization method using a single hydrophone. The methods are validated for the environment and configuration described in Section 3 for a signal-to-noise ratio of
localization method using a single hydrophone. The methods are validated for the environment and configuration described in Section 3 for a signal-to-noise ratio of  dB. The distance between source and hydrophone is equal to
dB. The distance between source and hydrophone is equal to  km. Source is deployed at
km. Source is deployed at  m of depth and the hydrophone is on the seabed.
m of depth and the hydrophone is on the seabed.
We first apply the deformation of the signal described in Section 4.2 for the Pekeris model. The parameters used to warp the modal signal are
-
(i)
water column depth:
 m;
m; -
(ii)
sound speed velocity in water:
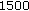 m/s;
m/s; -
(iii)
sound speed velocity in sediments:
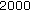 m/s;
m/s; -
(iv)
water density:
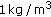 ;
; -
(v)
sediment density:
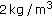 .
.
Within the parameters, the water column depth is a correct value, and other parameters are approximations of the real values to demonstrate robustness of the method.
Then, the  method allows a filtering of modes (classic bandpass filter applied on spectral representation given in Figure 13(b)), and these modes are analyzed for distance and depth estimation.
method allows a filtering of modes (classic bandpass filter applied on spectral representation given in Figure 13(b)), and these modes are analyzed for distance and depth estimation.
6.1.1. Distance
For the distance localization an access to mode phases is essential. First, a modal filtering by  is performed and then for each analyzed mode, its phase is calculated through a Fourier transform. Wavenumbers needed by the estimator defined in (19) are provided by Moctesuma.
is performed and then for each analyzed mode, its phase is calculated through a Fourier transform. Wavenumbers needed by the estimator defined in (19) are provided by Moctesuma.
In Figure 15 we show the cost function  corresponding to several distance estimations. As the distance estimator works on mode couples, we present five distance estimations for mode couples:
corresponding to several distance estimations. As the distance estimator works on mode couples, we present five distance estimations for mode couples:  ,
,  ,
,  ,
,  and
and  and research area
and research area  km with a step
km with a step  m. The estimated distances are given in Table 3 (the real distance is
m. The estimated distances are given in Table 3 (the real distance is  km). The first
km). The first  estimations are correct, and the last one is false, which is due to limited frequency band of mode
estimations are correct, and the last one is false, which is due to limited frequency band of mode  . Moreover, the sign-distance estimator provides mode signs. For this example, the mode signs were estimated on the same mode couples as distance. The estimation of mode signs no.
. Moreover, the sign-distance estimator provides mode signs. For this example, the mode signs were estimated on the same mode couples as distance. The estimation of mode signs no.  to
to  is correct and the absolute signs are
is correct and the absolute signs are  ,
,  ,
,  ,
,  ,
,  and
and  .
.
 approach.
approach.Cost functions C of sign-distance estimator in a single hydrophone scenario. The results are given for mode couples: (2,1), (3,1), (4,2), (5,3), and (6,4) and radial distance search zone r ∊ (8,13) km. The source is 10 km distant from the hydrophone. Solid and dashed lines are given for two possible values of  : 0 and π.
: 0 and π.
6.1.2. Depth
For depth localization an estimation of mode excitation factors is needed. First, a modal filtering is performed on real and simulated data by  approach, and then for each analyzed mode, its mode excitation factor modulus is calculated as a mean over frequency. Moreover, mode signs estimated above can be used in the contrast function
approach, and then for each analyzed mode, its mode excitation factor modulus is calculated as a mean over frequency. Moreover, mode signs estimated above can be used in the contrast function  .
.
In Figure 16 we show the result of depth localization. The performance is given for the methods "without mode signs" and "with mode signs." The difference in performance between two methods is relevant which results from the importance of taking into account mode signs when calculating the contrast function  . The method "with mode signs" eliminates the "mirror solutions" (decrease of the contrast function
. The method "with mode signs" eliminates the "mirror solutions" (decrease of the contrast function  from
from  dB to
dB to  dB for a secondary peak at
dB for a secondary peak at  m by adding mode signs). Figure 17 highlights also a problem that can appear when adding mode signs: if the mode sign estimation is false (here, sign of mode
m by adding mode signs). Figure 17 highlights also a problem that can appear when adding mode signs: if the mode sign estimation is false (here, sign of mode  is false), then the localization performance decreases significantly. However, as one can choose between
is false), then the localization performance decreases significantly. However, as one can choose between  options when estimating mode signs (the current mode sign
options when estimating mode signs (the current mode sign  is estimated using three inferior modes
is estimated using three inferior modes  ), the probability of this error should decrease (if the signal-to-noise ratio is sufficiently high).
), the probability of this error should decrease (if the signal-to-noise ratio is sufficiently high).
Contrast functions G for depth source localization by TFa approach with false mode sign estimation. The mode sign no. 3 is estimated with an error (estimated as negative, but should be positive). The configuration localization is the same as in Figure 16.
Due to the oscillating character of modal functions and because we consider only modal function modulus, there exist "mirror" depths which give secondary peaks in the contrast function  (Figure 14(a)). To explain this fact and the reason why they disappear when integrating mode signs in the depth estimation, let us present an example. Figure 18 shows
(Figure 14(a)). To explain this fact and the reason why they disappear when integrating mode signs in the depth estimation, let us present an example. Figure 18 shows  mode excitation factors extracted from simulated data at two different source depths:
mode excitation factors extracted from simulated data at two different source depths:  m and
m and  m. For these two depths the mode excitation factor moduli are almost the same (Figure 18(a)), and so the difference in the contrast function for these depths is not relevant. When the complete information about mode excitation factors (i.e., modulus and sign) is considered (Figure 18(b)), these depths become discriminated. This is due to especially modes no.
m. For these two depths the mode excitation factor moduli are almost the same (Figure 18(a)), and so the difference in the contrast function for these depths is not relevant. When the complete information about mode excitation factors (i.e., modulus and sign) is considered (Figure 18(b)), these depths become discriminated. This is due to especially modes no.  ,
,  , but also
, but also  .
.
In the mono-dimensional configuration in lower signal-to-noise ratio conditions the mode sign and distance estimations can be inaccurate. Also, the depth localization performance cannot be satisfied. Therefore, we propose the multi-dimensional configuration that is more robust and efficient due to a richer information about the source and the environment recorded on the HLA.
6.2. Horizontal Line Array
This section presents results of localization in distance and in depth using  approach. The objective is to show the performance of
approach. The objective is to show the performance of  localization method. The methods are validated in the environment and configuration described in Section 3 for a signal-to-noise ratio of
localization method. The methods are validated in the environment and configuration described in Section 3 for a signal-to-noise ratio of  dB. The distance between the source and the first hydrophone of HLA is
dB. The distance between the source and the first hydrophone of HLA is  km. The source depth is
km. The source depth is  m and the HLA is on the seabed.
m and the HLA is on the seabed.
According to the Shannon theorem and for the ULF band ( Hz) the maximal spatial sampling should be done every
Hz) the maximal spatial sampling should be done every  m. Thus, in theory we could consider every second HLA hydrophone without any information lost (as the whole HLA samples linearly the space every
m. Thus, in theory we could consider every second HLA hydrophone without any information lost (as the whole HLA samples linearly the space every  m). However, with a higher space sampling, better noise canceling algorithms can be implemented. What is more important, is a length of the HLA. When the length of HLA reduces, the localization performance decreases. This is provoked by a spreading of the signal in the
m). However, with a higher space sampling, better noise canceling algorithms can be implemented. What is more important, is a length of the HLA. When the length of HLA reduces, the localization performance decreases. This is provoked by a spreading of the signal in the  plane which results from a not sufficiently long radial distance sampling of the modal signal [16]. Different issues of the use of HLA are discussed in [10].
plane which results from a not sufficiently long radial distance sampling of the modal signal [16]. Different issues of the use of HLA are discussed in [10].
The first step of the method is a  velocity correction which is done with the minimum value of the sound speed profile in water
velocity correction which is done with the minimum value of the sound speed profile in water  m/s. Then, the
m/s. Then, the  transform is calculated and this representation is used for mode filtering. These modes are then analyzed for distance and depth estimations.
transform is calculated and this representation is used for mode filtering. These modes are then analyzed for distance and depth estimations.
6.2.1. Distance
After  filtering, the phase of each mode is calculated through a Fourier transform. The wavenumbers needed by the estimator defined in (19) are provided by
filtering, the phase of each mode is calculated through a Fourier transform. The wavenumbers needed by the estimator defined in (19) are provided by  simulator. This estimation is applied to each hydrophone of the HLA (
simulator. This estimation is applied to each hydrophone of the HLA ( estimations) [16].
estimations) [16].
We apply the estimator on five different mode couples:  ,
,  ,
,  ,
,  ,
,  and
and  , and research erea
, and research erea  km with step
km with step  m. The estimated distance values are given in Figure 19 and its mean values are given in Table 4. Moreover, the sign-distance estimator gives as a result mode sign. In multi-dimensional case, we dispose of
m. The estimated distance values are given in Figure 19 and its mean values are given in Table 4. Moreover, the sign-distance estimator gives as a result mode sign. In multi-dimensional case, we dispose of  estimations of mode signs for each mode couple option. For a mode number equal to
estimations of mode signs for each mode couple option. For a mode number equal to  , the sign-distance estimator is applied on following mode couples:
, the sign-distance estimator is applied on following mode couples:  (for mode
(for mode  ),
),  ,
,  (for mode
(for mode  ),
),  ,
,  ,
,  (for mode
(for mode  ),
),  ,
,  ,
,  (for mode
(for mode  ),
),  ,
,  ,
,  (for mode
(for mode  ),
),  ,
,  and
and  (for mode
(for mode  ) and the user has to select the couple he wants to use. This information is used here to maximize the probability of correct choice within available options for each estimation step. As the mode sign estimation is sequential it is primordial to not commit an error at the beginning to avoid its propagation. At each step (for each mode sign estimation) a series of
) and the user has to select the couple he wants to use. This information is used here to maximize the probability of correct choice within available options for each estimation step. As the mode sign estimation is sequential it is primordial to not commit an error at the beginning to avoid its propagation. At each step (for each mode sign estimation) a series of  parameters is calculated to help the user in taking the decision. For the first step these parameters are calculated once (for the couple
parameters is calculated to help the user in taking the decision. For the first step these parameters are calculated once (for the couple  ), for the second step we dispose of two set of parameters (for the couples
), for the second step we dispose of two set of parameters (for the couples  and
and  ), and for the following steps we have always three sets of parameters. These parameters are defined as follows.
), and for the following steps we have always three sets of parameters. These parameters are defined as follows.
Choice reliability:

where  is a number of sign changes (
is a number of sign changes ( ). This criteria should be maximal.
). This criteria should be maximal.
Estimation variability:

where  denotes a set of
denotes a set of  distance estimations and
distance estimations and  denotes a second derivative with respect to the hydrophone number. For the no-error estimation of distance the first derivative is equal to interhydrophone distance. Then, the second derivative is equal to zero as the first derivative is a constant function. This criterion allows to measure the variability of distance estimations across all hydrophones and should be minimal.
denotes a second derivative with respect to the hydrophone number. For the no-error estimation of distance the first derivative is equal to interhydrophone distance. Then, the second derivative is equal to zero as the first derivative is a constant function. This criterion allows to measure the variability of distance estimations across all hydrophones and should be minimal.
Error distance estimation:

where  denotes a distance estimation for
denotes a distance estimation for  hydrophone at actual step analysis (
hydrophone at actual step analysis ( ) and
) and  denotes the final estimation of distance from previous step (
denotes the final estimation of distance from previous step ( ). This criterion allows cancel secondary peak solutions for which the first two criteria gave good results and should be obviously minimal.
). This criterion allows cancel secondary peak solutions for which the first two criteria gave good results and should be obviously minimal.
 m.
m.For the example presented here, the mode signs were estimated on the same mode couples as distance. The estimation of signs of modes no.  to
to  is correct and the absolute signs are
is correct and the absolute signs are  ,
,  ,
,  ,
,  ,
,  ,
,  and
and  .
.
6.2.2. Depth
After modal filtering, the mode excitation factor modulus of each mode is calculated as a mean over the  region. Moreover, the sign-distance estimator can be used for mode signs estimation.
region. Moreover, the sign-distance estimator can be used for mode signs estimation.
In Figure 20 we show the result of depth localization. The performance is given for method "without mode signs" and "with mode signs." The difference between both methods is relevant which confirms the importance of taking into account mode signs when calculating the contrast function  . The method "with mode signs" eliminates the "mirror solutions" (decrease of the contrast function from
. The method "with mode signs" eliminates the "mirror solutions" (decrease of the contrast function from  dB to
dB to  dB for a secondary peak at
dB for a secondary peak at  m by adding mode signs).
m by adding mode signs).
6.3. Source Spectrum Issue
In Section 5.3 we described a simple method of estimation of the source spectrum. Now, we quantify the impact of this estimation on depth localization.
Let us consider an example of depth localization in the environment described in Section 3. The source ULF-2 is located at  m of depth. As we do not know the spectral properties of the localized source we consider two cases.
m of depth. As we do not know the spectral properties of the localized source we consider two cases.
-
(i)
We use a source with flat spectrum for simulation of the replica field (source ULF-1)-common approach when unknown source.
-
(ii)
We estimate a source spectrum by the method defined in (29) and use it to simulate the replica field.
In Figure 21, we present spectrum of the source ULF-2 estimated by the proposed method (compare with Figure 4(d)). The results of localization without and with source spectrum estimation are shown in Figure 22. We can note that estimating the source spectrum improves considerably the localization performance (of about  dB in the example).
dB in the example).
Result of the source spectrum estimation for source ULF-2 (to be compared with Figure 4(d)).
Contrast functions G for depth source localization by F-K approach combined with source spectrum estimation. The simulation is given for source ULF-2 located at 70 m of depth and 10 km distant from the HLA. (a) shows the gain given by taking into account the estimated spectrum of an unknown source for localization method without mode signs. (b) shows this gain in case of localization algorithm with integrated mode signs into the contrast function.
Nevertheless, our method is designed for broadband sources. Therefore, even if spectral characteristics of the source are perfectly known, but present narrowband or comb-type structures, the localization performance decreases. The performance decrease due to nonbroadband source is higher than the gain due to acquaintance of source spectral characteristics.
7. Conclusion
In this paper we propose passive source localization in shallow water based on modal filtering and features extraction. The depth and distance of an Ultra Low Frequency source are estimated in the mono-dimensional configuration (a single hydrophone) and in the multi-dimensional configuration (a horizontal line array). The localization techniques are, respectively, based on adapted Fourier transform and frequency-wavenumber transform. In both representations modes are separable and thus can be filtered. We discuss modal filtering tools, then the localization itself is performed.
For distance estimation, we base our localization method on the analysis of mode phases. The proposed distance estimator is naturally combined with mode sign estimator. For depth localization, we use matched-mode processing, a technique that widely demonstrated its performance in a shallow water environment. The principle is based on comparison (by a contrast function) of mode excitation factors extracted from real data with a set of mode excitation factors (for simulated source depths) extracted from replica data (modeled with Moctesuma). We demonstrate that adding the mode signs to the mode excitation factor modulus improves significantly the localization performance in depth. We also propose a method of estimation of the source spectrum, which is very important for depth localization using Matched-Mode Processing.
The localization results, in depth and distance, obtained on signals simulated with Moctesuma in realistic geophysical conditions are very satisfactory and demonstrate the performance of the proposed methods.
References
Jensen FB, Kuperman WA, Porter MB, Schmidt H: Computational Ocean Acoustics. AIP Press, New York, NY, USA; 1994.
Baggeroer AB, Kuperman WA, Mikhalevsky PN: An overview of matched field methods in ocean acoustics. IEEE Journal of Oceanic Engineering 1993, 18(4):401-424. 10.1109/48.262292
Fawcett JA, Yeremy ML, Chapman NR: Matched-field source localization in a range-dependent environment. The Journal of the Acoustical Society of America 1996, 99(1):272-282. 10.1121/1.414538
Wilson GR, Koch RA, Vidmar PJ: Matched-mode localization. The Journal of the Acoustical Society of America 1998, 104(1):156-162. 10.1121/1.423265
Shang EC, Clay CS, Wang YY: Passive harmonic source ranging in waveguides by using mode filter. The Journal of the Acoustical Society of America 1985, 78(1):172-175. 10.1121/1.392554
Collison NE, Dosso SE: Regularized matched-mode processing for source localization. The Journal of the Acoustical Society of America 2000, 107(6):3089-3100. 10.1121/1.429338
Bogart CW, Yang TC: Comparative performance of matched-mode and matched-field localization in a range-dependent environment. The Journal of the Acoustical Society of America 1992, 92(4):2051-2068. 10.1121/1.405257
Kuperman WA, Hodgkiss WS, Song HC: Phase conjugation in the ocean: experimental demonstration of an acoustic time-reversal mirror. The Journal of the Acoustical Society of America 1998, 103(1):25-40. 10.1121/1.423233
Prada C, de Rosny J, Clorennec D, et al.: Experimental detection and focusing in shallow water by decomposition of the time reversal operator. The Journal of the Acoustical Society of America 2007, 122(2):761-768. 10.1121/1.2749442
Bogart CW, Yang TC: Source localization with horizontal arrays in shallow water: spatial sampling and effective aperture. The Journal of the Acoustical Society of America 1994, 96(3):1677-1686. 10.1121/1.410247
Nicolas B, Mars JI, Lacoume J-L: Source depth estimation using a horizontal array by matched-mode processing in the frequency-wavenumber domain. EURASIP Journal on Applied Signal Processing 2006, 2006:-16.
Le Touzé G, Nicolas B, Mars J, Lacoume J-L: Matched representations and filters for guided waves. IEEE Signal Processing Letters. In press
Baraniuk RG, Jones DL: Unitary equivalence: new twist on signal processing. IEEE Transactions on Signal Processing 1995, 43(10):2269-2282. 10.1109/78.469861
Yang TC: A method of range and depth estimation by modal decomposition. The Journal of the Acoustical Society of America 1987, 82(5):1736-1745. 10.1121/1.395825
Cristol X, Passerieux J-M, Fattaccioli D: Modal representations of transient sound pulses in deep and shallow environments, with investigations about detailed space and time correlation of propagated waves. MAST, 2006
Lopatka M, Nicolas B, Le Touzé G, et al.: Robust underwater localization of ultra low frequency sources in operational context. Proceedings of the Uncertainty Analysis in Modelling (UAM '09), 2009, Nafplion, Greece
Le Touzé G, Nicolas B, Mars JI, Lacoume J-L: Time-frequency representations matched to guided waves. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), 2006 3: 440-443.
Papandreou-Suppappola A, Murray R, Iem B-G, Boudreaux-Bartels GF: Group delay shift covariant quadratic time-frequency representations. IEEE Transactions on Signal Processing 2001, 49(11):2549-2564. 10.1109/78.960403
McClure M, Carin L: Matching pursuits with a wave-based dictionary. IEEE Transactions on Signal Processing 1997, 45(12):2912-2927. 10.1109/78.650250
Le Touzé G: localisation de source par petits fonds en UBF (1−100Hz) à l'aide d'outils temps-frequence, Ph.D. dissertation. INP, Grenoble, France; 2007.
Nicolas B, Le Touzé G, Mars JI: Mode sign estimation to improve source depth estimation. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '08), 2008, Las Vegas, Nev, USA 2437-2440.
Jesus SM: Normal-mode matching localization in shallow water: environmental and system effects. The Journal of the Acoustical Society of America 1991, 90(4):2034-2041. 10.1121/1.401631
Wilson JH, Rajan SD, Null JM: Inversion techniques and the variability of sound propagation in shallow water. IEEE Journal of Oceanic Engineering 1996, 21(4):321. 10.1109/JOE.1996.544043
Nicolas B, Mars J, Lacoume JL: Geoacoustical parameters estimation with impulsive and boat-noise sources. IEEE Journal of Oceanic Engineering 2003, 28(3):494-501. 10.1109/JOE.2003.816687
Le Touzé G, Mars JI, Lacoume J-L: Matched time-frequency representations and warping operator for modal filtering. Proceedings of the European Signal Processing Conference (EUSIPCO '06), September 2006, Florence, Italy
Acknowledgment
This work was supported by Project REI 07.34.026 from the Mission pour la Recherche et l'Innovation Scientifique (MRIS) of the Delegation Generale pour l'Armement (DGA-French Departement of Defense).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lopatka, M., Le Touzé, G., Nicolas, B. et al. Underwater Broadband Source Localization Based on Modal Filtering and Features Extraction. EURASIP J. Adv. Signal Process. 2010, 304103 (2010). https://doi.org/10.1155/2010/304103
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/304103
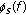 is the phase of the source at frequency
is the phase of the source at frequency 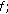
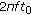 is a phase factor due to time delay
is a phase factor due to time delay 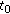 of the recorded signal;
of the recorded signal;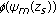 depends on the modal function sign at the source depth
depends on the modal function sign at the source depth 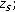 it is
it is  if
if 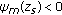 and
and  if
if 
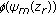 depends on the modal function sign at the receiver depth
depends on the modal function sign at the receiver depth 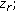
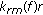 is a phase factor at frequency
is a phase factor at frequency  linked to the propagation distance
linked to the propagation distance  between source and receiver.
between source and receiver.




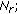
 ).
).

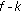 plane;
plane;





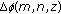 being difference between two mode phases at depth
being difference between two mode phases at depth  ; the values of this parameter are defined by (for details see Table
; the values of this parameter are defined by (for details see Table 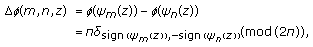
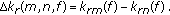

 m;
m;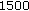 m/s;
m/s;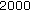 m/s;
m/s;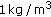 ;
;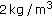 .
.






