- Research Article
- Open access
- Published:
Optimal Policy of Cross-Layer Design for Channel Access and Transmission Rate Adaptation in Cognitive Radio Networks
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 305145 (2010)
Abstract
In this paper, we investigate the cross-layer design of joint channel access and transmission rate adaptation in CR networks with multiple channels for both centralized and decentralized cases. Our target is to maximize the throughput of CR network under transmission power constraint by taking spectrum sensing errors into account. In centralized case, this problem is formulated as a special constrained Markov decision process (CMDP), which can be solved by standard linear programming (LP) method. As the complexity of finding the optimal policy by LP increases exponentially with the size of action space and state space, we further apply action set reduction and state aggregation to reduce the complexity without loss of optimality. Meanwhile, for the convenience of implementation, we also consider the pure policy design and analyze the corresponding characteristics. In decentralized case, where only local information is available and there is no coordination among the CR users, we prove the existence of the constrained Nash equilibrium and obtain the optimal decentralized policy. Finally, in the case that the traffic load parameters of the licensed users are unknown for the CR users, we propose two methods to estimate the parameters for two different cases. Numerical results validate the theoretic analysis.
1. Introduction
In recent years, the explosive growth of wireless devices and traffic incurs a dramatic increase of the requirement for radio spectrum resource. Unfortunately, as most of the spectrum resource suitable for wireless communications has been assigned, the available spectrum resources become scare. As today's spectrum is managed under a fixed assignment policy, which is highly inefficient in terms of spectrum utilization [1, 2], cognitive radios are adopted to sense their environments and promptly reconfigure their communication parameters based on their observations [3–5].
In CR networks, a new spectrum access method, namely dynamic spectrum access (DSA), is employed to improve spectrum utilization by allowing CR users to access the idle licensed spectrum bands without colliding with the active licensed users [6]. In multi-user environment, the DSA design should also consider the collision with other CR users. Meanwhile, CR users should take the power consumption into account. Furthermore, the time-varying fading nature of radio channel complicates adaptive access and transmission techniques. The solution to above problems asks for cross-layer design between physical layer and upper layers.
Recently, the issue of cross-layer design for dynamic spectrum access has attracted many researchers' efforts. Zhao et al. present a decentralized cognitive medium access control protocol under the framework of partially observable Markov decision process for ad hoc network [7]. This work is then extended by [8] to maximize the expected number of information bits delivered by an unlicensed user before its total energy is exhausted. Kim and chin [9] propose a MAC-layer sensing framework and energy-efficient dynamic sensing mode selection algorithm. The design of spectrum sensing and access strategies in the presence of spectrum sensing errors has been addressed in [10–13]. On the other hand, spectrum opportunity sharing among CR users is discussed in [14–17]. In [18, 19], the authors consider the power control in CDMA system under power constraint by formulating a stochastic game model to solve the problem. However, their assumptions of the transmission reward and the channel state in these works are not practical for fading channels. Besides, they do not consider multichannel case. In fact, to the best of our knowledge, there is little work focusing on the cross-layer design under the power constraint by taking the time-varying characteristics of the channel state and the collisions (both the collisions with primary user and the collisions with other CR users) into account. In this paper, we consider cross-layer design of multichannel access and transmission rate adaptation in CR network for both centralized and decentralized cases by taking the time-varying characteristics of channel state into account.
We consider the coexistence of a CR network with a licensed wideband wireless communications network. In centralized case, the cross-layer design problem can be modeled by constrained Markov decision process (CMDP) and solved by a dynamic programming method to achieve the optimal performance. In decentralized case, each CR user only knows its local information and should take actions to maximize the total performance of the whole CR network. We prove the existence of the constrained Nash equilibrium and calculate the optimal decentralized policy.
Another key difference between our approach and that of the above references is that complexity reduction is explicitly taken into account in our method. In both centralized and decentralized cases, the complexity of finding optimal policy increases exponentially with the size of action space and state space, which incurs the so-called curse of dimensionality. To overcome this problem, we perform action set reduction and state aggregation to reduce the complexity without loss of optimality. Under certain condition, we further prove that the multichannel access and transmission rate adaptation policy design can be solved separately in each channel without loss of optimality.
Furthermore, we observe that pure policy is preferred in practical environment due to the convenience of implementation and evaluation. Pure policies take action with deterministic rule. We name all the stationary polices as mixed polices and analyze the difference between pure polices and mixed polices in our proposed cross-layer design. This issue has attracted little attention in exiting researches.
In CR network, the change of white space or spectrum hole utilized for unlicensed communication depends on the spectrum occupancy of licensed users. But the CR users do not know the traffic load parameters of licensed users generally. In this case, we proposed two methods to estimate the traffic load parameters of licensed user.
The remaining part of the paper is organized as follows. In Section 2, the system model is described. The cross-layer design problem is formulated and discussed for both centralized and decentralized cases in Section 3. The complexity reduction of optimal policy design is considered in Section 4, in which we discuss the action set reduction and state aggregation and prove that the multichannel access and transmission rate adaptation policy design can be solved separately in each channel without loss of optimality under certain condition. Section 5 investigates the optimal pure policy design. In Section 6, the estimation methods for the unknown traffic load parameters of licensed user are provided. The numerical result is presented and discussed in Section 7. Finally, we conclude our work and point out the future work in Section 8.
2. System Model
In this paper, we consider the coexistence of a CR network with a licensed wideband wireless communications network. We refer to the wideband channel as licensed channel in this paper. The CR network consists of  CR users and a base station. The wideband channel of the wideband network is divided into
CR users and a base station. The wideband channel of the wideband network is divided into  narrowband channels (or subchannels, subcarriers) that are utilized by the
narrowband channels (or subchannels, subcarriers) that are utilized by the  CR users for opportunistic uplink packet transmission. Each narrowband channel can be used by only one CR user in each frame.
CR users for opportunistic uplink packet transmission. Each narrowband channel can be used by only one CR user in each frame.
The transmission model for every CR user is shown in Figure 1. At the data link layer, for the transmission capacity analysis, the infinite buffer of the transmitter is assumed to be continually backlogged with packets that must be transmitted to the base station and the channel selection is decided by every CR user. At the physical layer, the CR users operate over the selected parallel block fading channels and send data to the CR base station. These channels compose one (or a part of) licensed channel. To maximize the spectral efficiency, adaptive modulation (AM) [20] is utilized for each selected channel. In centralized case, the base station makes the whole decision. In decentralized case, the intelligent controller in each CR user performs cross-layer channel selection and rate selection in frame-by-frame manner. Furthermore, the intelligent controller should include some extra function blocks. First, the controller should calculate the immediate reward and cost for the optimal policy design. Second, in order to reduce complexity, the function block of action set reduction and state aggregation should be included in the intelligent controller. Finally, in the case that the traffic load parameters of licensed users are unknown, the controller should estimate them.
The frame structure is depicted in Figure 2. In Figure 2, the time-axis is divided into contiguous slots of equal duration, which correspond to frames with fixed-length of  . Channel sensing time is
. Channel sensing time is  . For notational convenience and without loss of generality, it is assumed that
. For notational convenience and without loss of generality, it is assumed that  is fairly small. For CR user
is fairly small. For CR user  , the probability of sensing false alarm and sensing miss detection are defined as
, the probability of sensing false alarm and sensing miss detection are defined as  and
and  , respectively. We assumed that the channel availabilities for the whole CR network are the same. Once the sensing result is idle, the CR user can transmit pilot to the base station to obtain the channel state information (CSI). It is assumed that the CSI could be fed back correctly without delay if the sensing result is correct, otherwise the collision could occur and the CSI cannot be fed back. Finally, if the CSI is fed back correctly, the CR users can take packets from the buffer, map them into symbols and select a transmission rate to send them to base station in both centralized and decentralized cases. At the end of each frame, the base station acknowledges every successful or unsuccessful transmission by error-free ACK or NAK, respectively.
, respectively. We assumed that the channel availabilities for the whole CR network are the same. Once the sensing result is idle, the CR user can transmit pilot to the base station to obtain the channel state information (CSI). It is assumed that the CSI could be fed back correctly without delay if the sensing result is correct, otherwise the collision could occur and the CSI cannot be fed back. Finally, if the CSI is fed back correctly, the CR users can take packets from the buffer, map them into symbols and select a transmission rate to send them to base station in both centralized and decentralized cases. At the end of each frame, the base station acknowledges every successful or unsuccessful transmission by error-free ACK or NAK, respectively.
For specific spectrum sensing method, such as energy detection,  and
and  can be calculated if the average signal-to-noise ratio (SNR) of the licensed user is known [12]. In this paper, we assume the spectrum sensing mechanisms are fixed for both centralized and decentralized cases.
can be calculated if the average signal-to-noise ratio (SNR) of the licensed user is known [12]. In this paper, we assume the spectrum sensing mechanisms are fixed for both centralized and decentralized cases.
In centralized case, the CR users cooperatively sense the licensed channel. The licensed channel is assumed busy only if the sensing result of every CR user is busy and the probability of false alarm is  . By suitable broadcasting mechanism, it is reasonable to assume that the sensing result is identical within the whole CR network. In this case, base station knows the CSI and the power constraint for each CR user and acts as a single controller to design the optimization policy for the whole network.
. By suitable broadcasting mechanism, it is reasonable to assume that the sensing result is identical within the whole CR network. In this case, base station knows the CSI and the power constraint for each CR user and acts as a single controller to design the optimization policy for the whole network.
In decentralized case, the CR users sense the licensed channel separately and only local CSI is available to each CR user and there is no coordination among the CR users. Therefore, the CR users should design cross-layer policy separately.
2.1. Licensed Channel Availability Model
In DSA system, time-varying channel availability should be considered according to the traffic load variation of licensed users, which is assumed to be independent and identically distributed (i.i.d.) alternative renewal process with ON (busy, 0) and OFF (idle, 1) periods [9]. The duration of an ON (OFF) period of channel  is described by an exponentially distributed stochastic variable with parameter
is described by an exponentially distributed stochastic variable with parameter  (
( ). If CR user sends the pilot and data symbols to the base station without incurring collision with licensed users during a frame, that is, the channel keeps idle during the frame, an opportunity is exploited as a stochastic variable and depends on recent sensing result. Before further discussion, we give the following definition at first.
). If CR user sends the pilot and data symbols to the base station without incurring collision with licensed users during a frame, that is, the channel keeps idle during the frame, an opportunity is exploited as a stochastic variable and depends on recent sensing result. Before further discussion, we give the following definition at first.
Definition 1.
Duration probability denotes the probability that at a specified time instant
denotes the probability that at a specified time instant  , the availability state for a specific licensed channel is
, the availability state for a specific licensed channel is  and this licensed channel will keep
and this licensed channel will keep  for an interval
for an interval  if the availability state starts with
if the availability state starts with  at
at  .
.
According to availability state  , the opportunity probability is
, the opportunity probability is  , and the collision probability is
, and the collision probability is  . The expression of
. The expression of  can be expressed as [21, 22]
can be expressed as [21, 22]

Then we can get  and
and  .
.
2.2. Evolution of Sensing Results
Let  denote the space of sensing results. To derive the state transition probabilities of
denote the space of sensing results. To derive the state transition probabilities of  , we define point probability as follows.
, we define point probability as follows.
Definition 2.
Point probability  denotes the probability that licensed channel availability is
denotes the probability that licensed channel availability is  at time
at time  if it starts with
if it starts with  at
at  .
.
According to Definitions 1 and 2, we can consider point probability as duration probability with interval of duration  . Meanwhile, it is obvious that the licensed channel availability at the beginning of a frame only depends on the licensed channel availability state obtained in the preceding frame. In addition, the probabilities of sensing false alarm and sensing miss detection are unchanged for each frame. Note that the miss detection of spectrum sensing can be found by pilot symbols. Therefore, the miss detection of spectrum sensing does not affect the change of sensing result and the sensing result of licensed channel can be molded as an ergodic finite state discrete time Markov chain with state space
. Meanwhile, it is obvious that the licensed channel availability at the beginning of a frame only depends on the licensed channel availability state obtained in the preceding frame. In addition, the probabilities of sensing false alarm and sensing miss detection are unchanged for each frame. Note that the miss detection of spectrum sensing can be found by pilot symbols. Therefore, the miss detection of spectrum sensing does not affect the change of sensing result and the sensing result of licensed channel can be molded as an ergodic finite state discrete time Markov chain with state space  . Furthermore, according to Definitions 1 and 2, the state transition probabilities of
. Furthermore, according to Definitions 1 and 2, the state transition probabilities of  can be given as:
can be given as:

where  =
=  in centralized case or
in centralized case or  in decentralized case.
in decentralized case.
2.3. Rate and Power Adaptation Model
We consider a block fading model to characterize the  parallel narrowband channels, that is, these channels keep constant during each frame. It is well known that block fading channel can be modeled as an ergodic first order finite state discrete time Markov channel (FSMC) [23]. Let
parallel narrowband channels, that is, these channels keep constant during each frame. It is well known that block fading channel can be modeled as an ergodic first order finite state discrete time Markov channel (FSMC) [23]. Let  be a sequence of pre-selected thresholds of received SNR and
be a sequence of pre-selected thresholds of received SNR and  denote the channel state space of
denote the channel state space of  th channel for CR user
th channel for CR user  . The probability distribution of state space
. The probability distribution of state space  can be given as
can be given as  ,
,  , where
, where  is the average SNR. Therefore, the state transition probabilities of the
is the average SNR. Therefore, the state transition probabilities of the  th channel are
th channel are

where  , and
, and  is maximal Doppler frequency of CR user
is maximal Doppler frequency of CR user  [23]. For CR users
[23]. For CR users  , the composite state space of
, the composite state space of  channels is denoted by
channels is denoted by  , and
, and  . Correspondingly, the composite channel state is defined as
. Correspondingly, the composite channel state is defined as  , where
, where  . If it is assumed that the state transition probabilities between each pair of channels are independent [24] and the transition probability of
. If it is assumed that the state transition probabilities between each pair of channels are independent [24] and the transition probability of  is given by
is given by  .
.
In the proposed system, adaptive transmission scheme based on M-ary quadrature amplitude modulation (M-QAM) is employed for each channel. Let  denote the transmission rate space of each channel, in which
denote the transmission rate space of each channel, in which  is corresponding to
is corresponding to  -QAM transmission. Specifically, 0 and 1 are corresponding to no transmission and BPSK transmission, respectively. For given transmission rate, power, and channel state, the bit error rate (BER) can be estimated. Assuming ideal coherent detection, BER bound for
-QAM transmission. Specifically, 0 and 1 are corresponding to no transmission and BPSK transmission, respectively. For given transmission rate, power, and channel state, the bit error rate (BER) can be estimated. Assuming ideal coherent detection, BER bound for  is given by [20],
is given by [20],

For  ,
,

where  is noise power. According to (5) and (6), the pessimistic minimum power
is noise power. According to (5) and (6), the pessimistic minimum power  can be calculated to achieve a specified BER bound for channel state k and transmission rate
can be calculated to achieve a specified BER bound for channel state k and transmission rate  .
.
3. Problem Formulation and Discussion
In this section, we consider the cross-layer policy design of the channel access and transmission rate adaptation where each CR user aims at maximizing expected long-term average reward under power constraint. We define the reward as the number of packets successfully transmitted to base station per frame. The policy design will be formulated and discussed in both centralized and decentralized cases.
3.1. Preliminary Definition
To model the stochastic characteristics of the CR networks considered in this paper, we first provide the definition of  , where
, where  is state space and
is state space and  ,
, ,
, ,
, are action space, state transition probability matrix, reward, and cost, respectively.
are action space, state transition probability matrix, reward, and cost, respectively.
We can define a composite CR network state space  instinctively, where the notation "
instinctively, where the notation " " denotes the Cartesian product. Let
" denotes the Cartesian product. Let  . Then,
. Then,  can be further expressed as
can be further expressed as  . The state transition probabilities of
. The state transition probabilities of  depend on transition probabilities of composite channel state and sensing result. We assume that sate transition only occurs at the beginning of each frame. Let
depend on transition probabilities of composite channel state and sensing result. We assume that sate transition only occurs at the beginning of each frame. Let  denote the whole CR network state at the beginning of a frame. The CR network evolves into a new state
denote the whole CR network state at the beginning of a frame. The CR network evolves into a new state  at the beginning of the next frame. In this paper, it is assumed that the transition probabilities of composite channel state and channel sensing result are independent of each other [8, 25]. We can express the transition probability as
at the beginning of the next frame. In this paper, it is assumed that the transition probabilities of composite channel state and channel sensing result are independent of each other [8, 25]. We can express the transition probability as

We define  to be the steady state probabilities of
to be the steady state probabilities of  . In the similar way, for each CR user, we can define the local state space
. In the similar way, for each CR user, we can define the local state space  and the steady state probability vector
and the steady state probability vector  .
.
The access action set is defined as  , where
, where  means that CR user
means that CR user  chooses channel
chooses channel  to access and
to access and  means the opposite. We also define the transmission rate space as
means the opposite. We also define the transmission rate space as  .
.
Therefore, for CR user  , we can define the local action space
, we can define the local action space  , which consists of all access decision and transmission rate decision. The action space of whole CR network can be expressed as
, which consists of all access decision and transmission rate decision. The action space of whole CR network can be expressed as  .
.
In  th decision period (
th decision period ( th frame), if the action of the whole CR network is
th frame), if the action of the whole CR network is  and the state is
and the state is  , the reward for the CR user
, the reward for the CR user  is given by
is given by

where  is the sensing result at the beginning of
is the sensing result at the beginning of  th frame, and
th frame, and  is the number of transmitted packets in a frame.
is the number of transmitted packets in a frame.  is a linear increasing function and is defined as
is a linear increasing function and is defined as  for simplification in this paper. If another CR user also accesses channel
for simplification in this paper. If another CR user also accesses channel  , the collision occurs and the reward on the channel
, the collision occurs and the reward on the channel  will be 0. We also assume that the packet loss due to transmission failure is only determined by the collision with licensed users when the BER is small enough.
will be 0. We also assume that the packet loss due to transmission failure is only determined by the collision with licensed users when the BER is small enough.  is the probability that the licensed channel is idle during
is the probability that the licensed channel is idle during  when sensing result of CR user
when sensing result of CR user  is
is  .
.
For CR user  , the cost is defined as power consumption and given by
, the cost is defined as power consumption and given by

where  is defined in (4) and (5). For CR user
is defined in (4) and (5). For CR user  , the expected long-term average power consumption should be upper bounded by the threshold
, the expected long-term average power consumption should be upper bounded by the threshold  , that is,
, that is,

3.2. Centralized Optimization
We firstly consider maximizing the total expected long-term average reward of the whole CR network in centralized case. This means we should find an optimal policy  as
as

where  is the set of centralized policies.
is the set of centralized policies.
This problem can be formulated as a special Constrained Markov Decision Process (CMDP). That is, the state transition probabilities of the CMDP proposed in this section are not affected by action. According to [26, Theorem  ], the standard LP approach for this problem can be formulated as
], the standard LP approach for this problem can be formulated as

where occupation measure  is a variable. By solving (11), we can get the optimal value
is a variable. By solving (11), we can get the optimal value  for each
for each  pair and the corresponding optimal policy
pair and the corresponding optimal policy  can be obtained by
can be obtained by

which stands for the probability that the action  is chosen when the network state is
is chosen when the network state is  .
.
3.3. Decentralized Case
In decentralized case, each CR user does not know any information except the probability of sensing false alarm  , steady state probabilities
, steady state probabilities  , and the power threshold
, and the power threshold  . We define
. We define  as the class of decentralized policies. As mentioned in the previous section, the CR users aim at maximizing the total reward of the whole CR network. It means that all CR users have the common maximizing object
as the class of decentralized policies. As mentioned in the previous section, the CR users aim at maximizing the total reward of the whole CR network. It means that all CR users have the common maximizing object

where  and
and  can be expressed as
can be expressed as  and
and  , respectively.
, respectively.
For a policy  , we define
, we define  as the subset of u by deleting the
as the subset of u by deleting the  th component. We further define
th component. We further define  as all CR users except user
as all CR users except user  use the element in
use the element in  whereas user
whereas user  uses the policy
uses the policy  .
.
Definition 3.
 is a constrained Nash equilibrium [27] if it satisfies the power constraints (9) for all users and
is a constrained Nash equilibrium [27] if it satisfies the power constraints (9) for all users and

for any  such that the power constraints are satisfied for the policy
such that the power constraints are satisfied for the policy  .
.
Theorem 1.
Any policy  maximizing (13) while satisfying the power constraints (9) is a constrained Nash equilibrium in this cooperative game.
maximizing (13) while satisfying the power constraints (9) is a constrained Nash equilibrium in this cooperative game.
Proof.
Assume policy u maximizing (13) satisfies the power constraints but is not a constrained Nash equilibrium. According to Definition 3, there must exist a CR user  and the policy
and the policy  , such that the power constraint of this CR user
, such that the power constraint of this CR user  holds and
holds and  . Furthermore, based on (8), the power constraints of all CR users can be satisfied by the policy
. Furthermore, based on (8), the power constraints of all CR users can be satisfied by the policy  . This result contradicts with the assumption that the policy u maximizes (13). Therefore, we conclude that
. This result contradicts with the assumption that the policy u maximizes (13). Therefore, we conclude that  is a constrained Nash equilibrium.
is a constrained Nash equilibrium.
Lemma 1.
All CR users can calculate the optimal policy  by solving the same optimization problem
by solving the same optimization problem

where  is necessarily a constrained Nash equilibrium and also a globally optimal policy in decentralized case.
is necessarily a constrained Nash equilibrium and also a globally optimal policy in decentralized case.
Proof.
Problem (15) can be formulated as

where  is the occupation measure of local state and local action of CR user
is the occupation measure of local state and local action of CR user  . Each CR user solves the same optimization problem (16) and the corresponding optimal policy
. Each CR user solves the same optimization problem (16) and the corresponding optimal policy  can be obtained similarly as (12). The solution
can be obtained similarly as (12). The solution  must be a constrained Nash equilibrium and a globally optimal policy in decentralized case.
must be a constrained Nash equilibrium and a globally optimal policy in decentralized case.
In the case that the CR network just has two CR users, the globally optimal policy can be simply calculated. By defining  and
and  , the problem (16) can be expressed as
, the problem (16) can be expressed as

4. Simplification of Policy Design
With  rates,
rates,  channel states,
channel states,  channels, and CR users
channels, and CR users  , the LP (11) has
, the LP (11) has  variables and the LP (17) has
variables and the LP (17) has  variables. The variables increase exponentially both in centralized and decentralized cases. Consequently, it is impossible to design the optimal policy in real-time in response to evolving parameters (
variables. The variables increase exponentially both in centralized and decentralized cases. Consequently, it is impossible to design the optimal policy in real-time in response to evolving parameters ( and
and  ). In this section, we simplify the LP (11) and (17) by reducing the variable number in two ways without loss of the optimality of the policy. One way is to transform the multichannel policy design to single channel policy design, while the other reduces action set and aggregates states. For the former method, we have the following theorem.
). In this section, we simplify the LP (11) and (17) by reducing the variable number in two ways without loss of the optimality of the policy. One way is to transform the multichannel policy design to single channel policy design, while the other reduces action set and aggregates states. For the former method, we have the following theorem.
Theorem 2.
Under the condition that the maximal Doppler frequency  is the same on every channel for the CR user
is the same on every channel for the CR user  , the policy design can be solved separately for each channel without loss of optimality.
, the policy design can be solved separately for each channel without loss of optimality.
Proof.
See Appendix .
In the case of single channel, the action set is  , where
, where  means that the CR user does not access this channel and
means that the CR user does not access this channel and  means that there is no data transmission. In fact, the access action
means that there is no data transmission. In fact, the access action  can be obtained in the transmission rate state
can be obtained in the transmission rate state  . Therefore, the action set can be further reduced and the reduced action set is defined as
. Therefore, the action set can be further reduced and the reduced action set is defined as  . On the other hand, any state
. On the other hand, any state  is aggregated into a macro-state
is aggregated into a macro-state  by state aggregation. Consequently, we have the following propositions.
by state aggregation. Consequently, we have the following propositions.
Proposition 1.
Based on Theorem 2, for the optimal policy design on each channel, the new action and state space of CR user  are respectively expressed as
are respectively expressed as  and
and  . The new action and state space of the whole CR network are respectively expressed as
. The new action and state space of the whole CR network are respectively expressed as  and
and  .
.
Proposition 2.
Based on Theorem 2 and Proposition 1, the action set reduction and state aggregation do not affect the optimality of the policy design. In addition, the optimal occupation measures  can be calculated according to the original occupation measures
can be calculated according to the original occupation measures  which correspond to the original optimal policy
which correspond to the original optimal policy  , that is,
, that is,

After the simplification of policy design, the variable number of centralized policy is reduced from  to
to  and the variable number of decentralized policy is reduced from
and the variable number of decentralized policy is reduced from  to
to  . Obviously, the complexity of the optimal policy design is largely reduced.
. Obviously, the complexity of the optimal policy design is largely reduced.
5. Pure Policy
It is noticed that the previous discussion on the optimal policy is based on the mixed policy. In fact, the controller prefers pure policy to mixed policy due to the convenience of implementation and evaluation. For pure policy, the action selection is not stochastic but only one action could be adopted for each state. The optimal pure policy exists for centralized case and the LP for the optimal pure policy can be formulated as

For decentralized case, we have the following theorems.
Theorem 3.
In decentralized case, the constrained Nash equilibrium exists under the condition of pure polices.
Proof.
Under the condition of pure policy, the state space and action space are finite and countable. Therefore, Theorem 1 still holds and the constrained Nash equilibrium exists under the condition of pure polices.
When  , we can get the optimal pure policy for decentralized case in similar way as (17).
, we can get the optimal pure policy for decentralized case in similar way as (17).
Theorem 4.
In decentralized case, Theorem 2 does not hold under the condition of pure polices.
Proof.
Note that under the condition of pure policy, the state space and action space are finite and countable. If the policy design is solved separately in every channel, the state space and action space actually are reduced and the optimality is not guaranteed.
6. Parameter Estimation
In CR network, the change of spectrum hole depends on the spectrum occupancy of licensed users. But the CR users do not know the traffic load parameters ( and
and  ) of licensed users generally. According to the analysis in the above sections, the design of optimal policy requires the knowledge about system state transition probabilities associated with the traffic load parameters. In this section, we estimate the traffic load parameters (
) of licensed users generally. According to the analysis in the above sections, the design of optimal policy requires the knowledge about system state transition probabilities associated with the traffic load parameters. In this section, we estimate the traffic load parameters ( and
and  ) of licensed users in the following two cases:
) of licensed users in the following two cases:
-
(1)
The value of parameter pair
 has the constant value
has the constant value  belongs to a fixed finite set
belongs to a fixed finite set 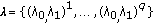 .
. -
(2)
There is no prior information about the value of parameter pair
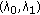 .
.
6.1. Fixed Finite Set
We construct the following adaptive control rule. At each frame  , the CR users make the maximum likelihood estimate
, the CR users make the maximum likelihood estimate  after the channel sensing phase
after the channel sensing phase

where  is the sensing result in frame
is the sensing result in frame  ,
,  (
( ,
, ;
; ,
, ) is the transition probability under the action
) is the transition probability under the action  , and the parameter value is
, and the parameter value is  .
.
Theorem 5.
The convergence of  is guaranteed by performing the maximum likelihood estimate of (20).
is guaranteed by performing the maximum likelihood estimate of (20).
Proof.
Mandi has given the convergence condition in [28] by stating that for each  if there exists
if there exists  so that
so that

then the convergence of  is guaranteed. Note that the transition probability of the sensing result is not affected by the action choice of CR users. It is obvious that (21) can be satisfied in this system and the convergence property is assured. Furthermore, the maximum likelihood estimation (20) can be simplified as
is guaranteed. Note that the transition probability of the sensing result is not affected by the action choice of CR users. It is obvious that (21) can be satisfied in this system and the convergence property is assured. Furthermore, the maximum likelihood estimation (20) can be simplified as

6.2. No Prior Information
We consider the first order moment estimation for the case of no prior information about the value of parameter pair  . The statistic transition probability matrix of sensing results can be defined as
. The statistic transition probability matrix of sensing results can be defined as

Based on sensing result, the statistic transition probability matrix can be updated frame by frame. In frame  , according to (2),
, according to (2),  can be estimated by the following equations
can be estimated by the following equations

7. Numerical Results
In this section, we present numerical results to evaluate the performances of the proposed policies in both centralized and decentralized cases. In the numerical computation, the number of CR users is set to be  . Traffic load parameters of licensed channel are given by
. Traffic load parameters of licensed channel are given by  ms and
ms and  ms. The length of frame
ms. The length of frame  ms and the spectrum sensing false alarm is set to be 0.1 for each CR user. Licensed channel is divided into
ms and the spectrum sensing false alarm is set to be 0.1 for each CR user. Licensed channel is divided into  narrow channels. To illustrate the influence of
narrow channels. To illustrate the influence of  on the performances of pure policies, we consider 3 different cases:
on the performances of pure policies, we consider 3 different cases:  ,
,  , and
, and  . Each channel has
. Each channel has  states, and
states, and  dB,
dB,  dB. Noise power
dB. Noise power  and target BER are set to be
and target BER are set to be  mW,
mW,  , respectively. Average SNR and maximal Doppler frequency of each channel are
, respectively. Average SNR and maximal Doppler frequency of each channel are  dB and
dB and  Hz, respectively. We adopt four modulation schemes which are BPSK, 4-QAM, 8-QAM, and 16-QAM. Then we have
Hz, respectively. We adopt four modulation schemes which are BPSK, 4-QAM, 8-QAM, and 16-QAM. Then we have  .
.
In Figure 3, throughput versus average power constraint for different policies in centralized case is presented. Due to the cooperative spectrum sensing, the sensing false alarm is 0.01 and the throughput is almost as same as the perfect spectrum sensing case (Note that the miss detection can be found by the pilot symbols). It can be seen that the mixed polices are not affected by the value of  and this result coincides with Theorem 2. We further notice that the throughput of pure policies is improved with the increase of
and this result coincides with Theorem 2. We further notice that the throughput of pure policies is improved with the increase of  . This coincides with Theorem 4. The reason which leads to this difference between mixed polices and pure polices is as follows. For pure polices, the number of occupation measure
. This coincides with Theorem 4. The reason which leads to this difference between mixed polices and pure polices is as follows. For pure polices, the number of occupation measure  in (19) is
in (19) is  and increases exponentially with
and increases exponentially with  . Then, the larger
. Then, the larger  is, the more feasible solutions to (19) are provided. On the other hand, the feasible solutions of mixed polices are infinite and uncountable. Moreover, we can find that all polices reach the throughput threshold as the power constraint increases. In this case, if one of the CR users gets the transmission chance, it always chooses the maximum transmission rate to transmit data.
is, the more feasible solutions to (19) are provided. On the other hand, the feasible solutions of mixed polices are infinite and uncountable. Moreover, we can find that all polices reach the throughput threshold as the power constraint increases. In this case, if one of the CR users gets the transmission chance, it always chooses the maximum transmission rate to transmit data.
In Figure 4, the throughputs of different polices in decentralized case are plotted with the different average power constraints. For sake of comparison, we also provide the result for perfect sensing. Generally, the throughputs of pure policies are improved with the increase of  . It is found that the optimal solutions of different
. It is found that the optimal solutions of different  are the same under certain power constraints. The reason is that in decentralized case, the number of feasible solutions is much less than that of the centralized case. Moreover, we can find that mixed policy and pure policy reach different throughput thresholds with the increase of power constraints. Note that in pure polices, if the channel state is
are the same under certain power constraints. The reason is that in decentralized case, the number of feasible solutions is much less than that of the centralized case. Moreover, we can find that mixed policy and pure policy reach different throughput thresholds with the increase of power constraints. Note that in pure polices, if the channel state is  (middle state) and the sensing result is idle, there are only two choices for each CR user which are transmission with probability one or keep silence with probability one. The latter choice is better than the first one and the threshold
(middle state) and the sensing result is idle, there are only two choices for each CR user which are transmission with probability one or keep silence with probability one. The latter choice is better than the first one and the threshold  is achieved in this case. This is why the threshold
is achieved in this case. This is why the threshold  is different with the threshold
is different with the threshold  .
.
Different with the centralized case, the sensing false alarm affects the performance obviously. Due to the sensing false alarm, the throughput threshold of pure polices  is less than the threshold
is less than the threshold  , which can only be reached by pure polices in perfect spectrum sensing case. For mixed polices, the throughput thresholds are the same. But in generally, the performance of imperfect sensing is less than that of the perfect sensing case.
, which can only be reached by pure polices in perfect spectrum sensing case. For mixed polices, the throughput thresholds are the same. But in generally, the performance of imperfect sensing is less than that of the perfect sensing case.
In Figure 5, the traffic load parameters pair ( and
and  ) of licensed users is estimated. In this case, we assume that the CR users have the prior knowledge that the constant value
) of licensed users is estimated. In this case, we assume that the CR users have the prior knowledge that the constant value  belongs to a fixed finite set
belongs to a fixed finite set  .
.  is set to be
is set to be  .
.
Figure 5 shows the change of the estimated parameters pair  with the increase of estimation frame number
with the increase of estimation frame number  . As expected, the convergence of
. As expected, the convergence of  is observed and coincides with Theorem 5.
is observed and coincides with Theorem 5.
In Figure 6, we estimate the traffic load parameters ( and
and  ) of licensed user in the case that no prior information is known about the value of parameter pair
) of licensed user in the case that no prior information is known about the value of parameter pair  . The constant value of
. The constant value of  is set to be (25 ms, 100 ms). It can be seen that, the estimated parameters
is set to be (25 ms, 100 ms). It can be seen that, the estimated parameters  approach to the constant value
approach to the constant value  with the increase of estimation frame number
with the increase of estimation frame number  . This observation coincides with the previous analysis.
. This observation coincides with the previous analysis.
8. Conclusions and Future Works
In this paper, we consider cross-layer design of joint channel access and transmission rate adaptation in CR networks in both centralized and decentralized cases. In centralized case, the cross-layer design can be solved by formulated as a special CMDP, and the optimal policy can be achieved. In decentralized case, we prove the existence of the constrained Nash equilibrium and characterize the structure of optimal decentralized policy. We point out that in both the centralized and decentralized cases, the complexity of finding optimal policy increases exponentially with the size of action space and state space, which incurs so-called curse of dimensionality. Therefore, we apply action set reduction and state aggregation to reduce the complexity without loss of optimality. We further prove that under certain condition, the multichannel access and transmission rate adaptation policy design can be solved separately with respect to every channel without loss of optimality. Furthermore, the pure polices are investigated and compared with the mixed polices. Finally, under the condition that the traffic load parameters of the licensed user are unknown for the CR users, we provide two different methods to estimate the parameters in two different cases.
In the future, we will extend our work to finite buffer with stochastic packet arrival and also concern the learning mechanism for the unknown CR environments.
References
Cabric D, O'Donnell ID, Chen MS-W, Brodersen RW: Spectrum sharing radios. IEEE Circuits and Systems Magazine 2006, 6(2):30-45. 10.1109/MCAS.2006.1648988
Devroye N, Mitran P, Tarokh V: Limits on communications in a cognitive radio channel. IEEE Communications Magazine 2006, 44(6):44-49.
Akyildiz IF, Lee W-Y, Vuran MC, Mohanty S: NeXt generation/dynamic spectrum access/cognitive radio wireless networks: a survey. Computer Networks 2006, 50(13):2127-2159. 10.1016/j.comnet.2006.05.001
Mitola J III, Maguire GQ Jr.: Cognitive radio: making software radios more personal. IEEE Personal Communications 1999, 6(4):13-18. 10.1109/98.788210
Haykin S: Cognitive radio: brain-empowered wireless communications. IEEE Journal on Selected Areas in Communications 2005, 23(2):201-220.
Zhao Q, Sadler BM: A survey of dynamic spectrum access. IEEE Signal Processing Magazine 2007, 24(3):79-89.
Zhao Q, Tong L, Swami A, Chen Y: Decentralized cognitive MAC for opportunistic spectrum access in ad hoc networks: a POMDP framework. IEEE Journal on Selected Areas in Communications 2007, 25(3):589-600.
Chen Y, Zhao Q, Swami A: Distributed spectrum sensing and access in cognitive radio networks with energy constraint. IEEE Transactions on Signal Processing 2009, 57(2):783-797.
Kim H, Shin KG: Efficient discovery of spectrum opportunities with MAC-layer sensing in cognitive radio networks. IEEE Transactions on Mobile Computing 2008, 7(5):533-545.
Chen Y, Zhao Q, Swami A: Joint design and separation principle for opportunistic spectrum access in the presence of sensing errors. IEEE Transactions on Information Theory 2008, 54(5):2053-2071.
Pei Y, Hoang AT, Liang Y-C: Sensing-throughput tradeoff in cognitive radio networks: how frequently should spectrum sensing be carried out? Proceedings of the 18th Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece 1-5.
Liang Y-C, Zeng Y, Peh ECY, Hoang AT: Sensing-throughput tradeoff for cognitive radio networks. IEEE Transactions on Wireless Communications 2008, 7(4):1326-1337.
Ghasemi A, Sousa ES: Optimization of spectrum sensing for opportunistic spectrum access in cognitive radio networks. Proceedings of the 4th Annual IEEE Consumer Communications and Networking Conference (CCNC '07), January 2007, Las Vegas, Nev, USA 1022-1026.
Liu H, Krishnamachari B, Zhao Q: Cooperation and learning in multiuser opportunistic spectrum access. Proceedings of the IEEE International Conference on Communications (ICC '08), May 2008, Beijing, China 487-492.
Liang Z, Liu W, Zhou P, Gao F: Randomized multi-user strategy for spectrum sharing in opportunistic spectrum access network. Proceedings of IEEE International Conference on Communications (ICC '08), May 2008, Beijing, China 477-481.
Liu K, Zhao Q, Chen Y: Distributed sensing and access in cognitive radio networks. Proceedings of the 10th IEEE International Symposium on Spread Spectrum Techniques and Applications (ISSSTA '08), August 2008, Bologna, Italy 23-27.
Liu H, Krishnamachari B: Randomized strategies for multi-user multi-channel opportunity sensing. Proceedings of IEEE Workshop on Cognitive Radio Networks (CCNC '08), January 2008
Altman E, Avratchenkov K, Bonneau N, Debbah M, El-Azouzi R, Menasché DS: Constrained stochastic games in wireless networks. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 315-320.
Altman E, Avrachenkov K, Miller G, Prabhu B: Discrete power control: cooperative and non-cooperative optimization. Proceedings of the 26th IEEE International Conference on Computer Communications (INFOCOM '07), May 2007, Anchorage, Alaska, USA 37-45.
Chung ST, Goldsmith AJ: Degrees of freedom in adaptive modulation: a unified view. IEEE Transactions on Communications 2001, 49(9):1561-1571. 10.1109/26.950343
Barlow RE, Hunter LC: Reliability analysis of a one-unit system. Operations Research 1961, 9(2):200-208. 10.1287/opre.9.2.200
Baxter LA: Availability measures for a two-state system. Journal of Applied Probability 1981, 18: 227-235. 10.2307/3213182
Wang HS, Moayeri N: Finite-state Markov channel—a useful model for radio communication channels. IEEE Transactions on Vehicular Technology 1995, 44(1):163-171. 10.1109/25.350282
Hossain MdJ, Djonin DV, Bhargava VK: Delay limited optimal and suboptimal power and bit loading algorithms for OFDM systems over correlated fading channels. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '05), November-December 2005, St. Louis, Mo, USA 5: 2787-2792.
Karmokar AK, Djonin DV, Bhargava VK: Optimal and suboptimal packet scheduling over time-varying flat fading channels. IEEE Transactions on Wireless Communications 2006, 5(2):446-457.
Altman E: Constrained Markov Decision Process: Stochastic Modeling. Chapman & Hall/CRC, London, UK; 1999.
Rosen JB: Existence and uniqueness of equilibrium points for concave N-person games. Econometrica 1965, 33(3):520-534. 10.2307/1911749
Mandi P: Estimation and control in Markov chains. Advances in Applied Probability 1974, 6: 40-60. 10.2307/1426206
Acknowledgments
The authors would like to thank Prof. Xuesong Tan for his valuable suggestions and help in preparing this paper and the two anonymous reviewers for their very helpful suggestions and comments. This work is supported in part by High-Tech Research and Development Program of China under Grant no. 2007AA01Z209, 2009AA011801, and 2009AA012002, National Fundamental Research Program of China under Grant A1420080150, and National Basic Research Program (973 Program) of China under Grant no. 2009CB320405, Nation Grand Special Science and Technology Project of China under Grant no. 2008ZX03005-001, National Natural Science Foundation of China under Grant no. 60702073, 60972029, and Special Project on Broadband Wireless Access sponsored by Huawei co., LTD.
Author information
Authors and Affiliations
Corresponding author
Appendices
A. Notations Table
Notations are listed in Table 1.
B. Proof of Theorem 1
Assume  is the optimal policy and the
is the optimal policy and the  is the solution of LP (11), the state
is the solution of LP (11), the state  and action
and action  can be expressed as
can be expressed as  and
and  , respectively. Here,
, respectively. Here,  and
and  are the corresponding state and action on channel
are the corresponding state and action on channel  . Based on
. Based on  , we can obtain the new occupation measure on channel
, we can obtain the new occupation measure on channel  as
as


Because the maximal Doppler frequency  of every channel is the same, each channel can be constructed as the same Markov chain and then the state transition matrix on each channel is the same. By defining
of every channel is the same, each channel can be constructed as the same Markov chain and then the state transition matrix on each channel is the same. By defining


we have


We define the new state space and action space:  ,
,  and formulate the new LP as
and formulate the new LP as


The occupation measure defined by (B.3) is also obtained in the feasible solution set of (B.4). Therefore, the policy design can be solved separately with respect to every channel without loss of optimality.
In the similar way, we can prove that Theorem 2 can also be applied to the decentralized case.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
He, H., Wang, J., Zhu, J. et al. Optimal Policy of Cross-Layer Design for Channel Access and Transmission Rate Adaptation in Cognitive Radio Networks. EURASIP J. Adv. Signal Process. 2010, 305145 (2010). https://doi.org/10.1155/2010/305145
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/305145


 .
. has the constant value
has the constant value  belongs to a fixed finite set
belongs to a fixed finite set 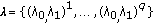 .
. .
.


