- Research Article
- Open access
- Published:
Superresolution versus Motion Compensation-Based Techniques for Radar Imaging Defense Applications
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 308379 (2010)
Abstract
Radar imaging of noncooperative targets is an interesting application of all-weather high-resolution coherent radars. However, these images are usually blurred when using the standard range-Doppler algorithm, if a long coherent processing interval (CPI) is used, and motion compensation techniques are hence necessary to improve imaging quality. If the CPI is reduced enough, target scatterers do not migrate of resolution cells and their corresponding Doppler frequencies are constant. Hence, for a short CPI, motion compensation is not longer necessary, but Doppler resolution gets degraded. In that case, superresolution algorithms may be applied. Here, we compare the superresolution-based focusing techniques with motion compensation-based methods. Our conclusion is that imaging quality after employing the superresolution approaches is not improved and, consequently, the use of motion compensation-based approaches to focus the radar images cannot be circumvented. Simulated and real data from high-resolution radars have been used to make the comparisons.
1. Introduction
Radar imaging based on a static high-resolution coherent radar is usually referred as Inverse Synthetic Aperture Radar (ISAR) imaging. ISAR may obtain range-Doppler images of noncooperative targets [1, 2], that is, targets whose motion is unknown. A large transmitted bandwidth guarantees a high slant-range resolution, whereas a large variation of the target aspect angle during the coherent processing interval (CPI) allows obtaining a fine cross-range resolution [3]. The slant-range and cross-range resolutions are, respectively, given by


where  is the light speed,
is the light speed,  is the transmitted bandwidth,
is the transmitted bandwidth,  is the transmitted wavelength, and
is the transmitted wavelength, and  is the variation of the target aspect angle during the CPI.
is the variation of the target aspect angle during the CPI.
In adverse meteorological conditions (such as fog or haze) and in defense and security applications, imaging sensors based on electro-optical wavelengths may have a reduced performance [4–6]. However, the ISAR technique, because of its all-weather feature, may still provide useful target images in those conditions. These images may subsequently be exploited by Automatic Target Recognition (ATR) algorithms [7–10].
In ISAR imaging, if the processing interval CPI is not too large, target scatterers do not migrate of resolution cells and their corresponding Doppler frequencies remain constant during the CPI. Hence, for this case, the standard range-Doppler algorithm (RDA) obtains focused ISAR images. However, these images are usually not adequate for subsequent ATR algorithms, because they have a degraded cross-range resolution, according to (2). Note that it is likely that the variation of the target aspect angle  is little for this short CPI.
is little for this short CPI.
On the contrary, if the CPI is large, the target scatterers migrate of resolution cells and the Doppler histories are complex functions. In this situation, RDA generates blurred ISAR images of decreased quality and motion compensation techniques are usually necessary to improve these ISAR products.
Moreover, the previous problem is exacerbated when the target is involved in complex motions, which is true for many practical cases. For example, maritime targets are usually involved in complex dynamics characterized by complicated yaw, pitch, and roll attitude motions [11].
Hence, in ISAR imaging of real noncooperative maneuvering targets, an important trade-off emerges; it is interesting to process a long CPI for achieving a fine cross-range resolution, but blurring effects arise for this long CPI because of the complex motion.
For a long CPI, the reason for scatterer migrations is quite obvious; the target scatterers have enough time to migrate of resolution cells. On the other hand, as far as the complex functions for the Doppler history are concerned, we can write the phase history of a target scatterer as [11]

where  is the central transmitted wavelength and
is the central transmitted wavelength and  is the range from the radar to the scatterer as a function of the slow-time
is the range from the radar to the scatterer as a function of the slow-time  .
.
If the target has a smooth constant rotational motion and the CPI is short, it can be shown [11] that a very accurate approximation of (3) is given by

where  is the range from the radar to the target rotation center,
is the range from the radar to the target rotation center,  is the cross-range position of the scatterer,
is the cross-range position of the scatterer,  is the slant-range position of the scatterer, and
is the slant-range position of the scatterer, and  is the effective rotation rate. If we suppose that
is the effective rotation rate. If we suppose that  does not change its position during the CPI, that is, translational motion compensation has previously been applied; the Doppler frequency associated to this scatterer is not a function of
does not change its position during the CPI, that is, translational motion compensation has previously been applied; the Doppler frequency associated to this scatterer is not a function of  :
:

Hence, according to (5), if the target motion is smooth, which is true for a reduced CPI, the Doppler frequency for each target scatterer is a constant and the standard RDA will generate a focused ISAR image. Take into account that the Doppler frequency is proportional to the cross-range position  of the scatterer.
of the scatterer.
On the other hand, according to (3), if the target is involved in complex motions and the CPI is large, the range from the radar to the scatterer  is a complex function and, consequently, the phase of the scatterer
is a complex function and, consequently, the phase of the scatterer  is also a complex function of the slow-time
is also a complex function of the slow-time  . This eventually implies that the scatterer Doppler frequency is not constant during the illumination interval CPI and, hence, if the standard RDA is applied, a severely blurred ISAR image is to be obtained. The problem rests in the fact that the processed CPI is too large and complex phase variations arise.
. This eventually implies that the scatterer Doppler frequency is not constant during the illumination interval CPI and, hence, if the standard RDA is applied, a severely blurred ISAR image is to be obtained. The problem rests in the fact that the processed CPI is too large and complex phase variations arise.
By trying to move away from motion compensation techniques, several authors have proposed to make use of superresolution techniques [12–17] to focus ISAR images. Because the blurring origin comes from a large CPI, the subjacent idea under the superresolution approach is based on reducing the observation interval CPI. As previously commented, for a reduced CPI, the target scatterers do not have enough time to experiment large variations of their Doppler frequencies or to migrate of resolution bins.
However, this CPI reduction certainly implies a loss of Doppler (cross-range) resolution. It is here where superresolution algorithms may theoretically improve the standard Fourier resolution. Hence, according to these approaches [12–17], focused ISAR images could be obtained without the necessity of processing long coherent intervals or of applying motion compensation algorithms.
In this paper, we compare the superresolution approaches with the results obtained after compensating the motion, by applying the methods to simulated and real data from complex targets. As far as the superresolution algorithms are concerned, we concentrate on the spectral estimation based on autoregressive (AR) coefficients [18], the multiple signal classification (MUSIC) estimator [19], and the Capon estimator [20].
Superresolution algorithms are based on parametric models of the signals and, consequently, they assume that the data satisfy some concrete hypotheses. In the ISAR scenario, we do not know to what extent the data match the models and, hence, the results are not as promising as expected. We have obtained images with many peaks whose positions do not necessarily correspond with the true locations of the scatterers. On the other hand, focusing indicators (such as entropy or contrast) may provide optimized values for the superresolution-based images because of their peaky nature. However, this is not indicative of an enhancement in the quality of the ISAR images, as discussed.
Our conclusion is that, when dealing with complex high-resolution radar data, the performance of the superresolution approach is not as good as expected and motion compensation methods should be applied if focused ISAR images are desired to be obtained.
Section 2 presents a brief introduction to RDA and motion compensation. In Section 3, the ISAR focusing technique based on superresolution algorithms is addressed. A brief description of the superresolution algorithms (AR, MUSIC, and Capon) is also given. Comparisons between superresolution and motion compensation-based techniques when using simulated data are presented in Section 4. Deep analyses of the obtained results in Section 4 let us derive important conclusions. After detailing the results achieved with live radar data in Section 5, some final conclusions conclude the paper in Section 6.
2. Range-Doppler Algorithm and Motion Compensation
The ISAR technique allows us to generate range-Doppler images of noncooperative targets. The standard image formation algorithm for ISAR is the range-Doppler algorithm (RDA) [11, 21], which may easily be described as follows.
-
(i)
Acquire a set of range profiles by using a coherent high-resolution radar and stack them to form the matrix
 , where
, where 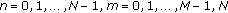 is the number of range bins, and
is the number of range bins, and 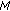 is the total number of acquired range profiles. Hence, the columns of
is the total number of acquired range profiles. Hence, the columns of 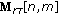 are the range profiles.
are the range profiles. -
(ii)
Apply a Fast Fourier Transform (FFT) to each range bin; that is, apply an FFT to each row of
 . The resulting matrix
. The resulting matrix 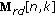 is the ISAR image generated by using RDA.
is the ISAR image generated by using RDA.
Figure 1 schematically shows the simple processing made by RDA.
Target motion may be divided into a translational component and a rotational component [21, 22]. With respect to the line-of-sight (LOS), the translational motion may further be decomposed into a radial (along-LOS) component and a tangential (across-LOS) component. The rotational motion is formed by the yaw, pitch, and roll attitude components.
In this context, the obtained ISAR image is a projection depending on target dynamics and orientation. Concretely, this ISAR projection plane is a plane formed by the LOS vector and a vector normal to the effective rotation vector  and contained in the plane perpendicular to LOS [22]. The effective rotation vector
and contained in the plane perpendicular to LOS [22]. The effective rotation vector  is the projection of the rotation vector
is the projection of the rotation vector  over the plane perpendicular to LOS.
over the plane perpendicular to LOS.
As an example, let us consider the scenario shown in Figure 2. A coherent high-resolution radar illuminates a pitching ship. The ship deck is aligned with LOS. In this case, the effective rotation vector  is just the pitch rotation vector
is just the pitch rotation vector  , as shown in Figure 2. The obtained ISAR image is a side view of the target.
, as shown in Figure 2. The obtained ISAR image is a side view of the target.
The rotational motion and the tangential translational motion may generate the desired Doppler gradient among scatterers situated in the same range bin. However, motion is also responsible for the possible appearance of blurring effects. Concretely, when the CPI is large and RDA is applied, the radial (along-LOS) component of the translational motion causes a large blurring in the ISAR images and the rest of motion may produce the so-called Migration Through Resolution Cells (MTRCs) [23].
Generally, before applying RDA, motion compensation techniques are necessary to improve the quality of the ISAR images. Thus, for translational motion compensation, two stages are often considered; range-bin alignment [1, 24–27] and phase adjustment [28–31]. On the other hand, for compensating the rotational motion, several methods may also be found in the literature [32–36].
In this paper, when dealing with motion compensation issues, we employ the extended envelope correlation method [26] for range-bin alignment, the entropy minimization approach [28] for phase adjustment, and the uniform-rate technique [36] for rotational motion compensation.
The focusing technique based on superresolution algorithms circumvents the use of motion compensation-based approaches, by reducing the CPI, as explained in the next section.
3. ISAR Focusing Technique Based on Superresolution Algorithms
The idea under applying superresolution algorithms for focusing ISAR images consists of processing the radar echoes for a reduced CPI in order to guarantee that scatterers do not have enough time to migrate of resolution cells or to experiment complex phase variations. More formally, by referring to Section 2, if we admit that  is a matrix whose columns are the range profiles, the ISAR focusing algorithm based on superresolution algorithms may be expressed as next indicated.
is a matrix whose columns are the range profiles, the ISAR focusing algorithm based on superresolution algorithms may be expressed as next indicated.
-
(i)
Consider a reduced number
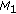 of range profiles of
of range profiles of 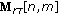 . This is equivalent to reducing the CPI. This simplified set may mathematically be expressed as
. This is equivalent to reducing the CPI. This simplified set may mathematically be expressed as 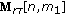 , where
, where 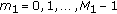 , with
, with 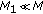 . The selection of
. The selection of 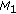 depends on the target dynamics.
depends on the target dynamics. -
(ii)
For the
 th range bin, estimate its high-resolution frequency content by applying a superresolution algorithm. That is, apply a superresolution technique to each row of
th range bin, estimate its high-resolution frequency content by applying a superresolution algorithm. That is, apply a superresolution technique to each row of 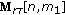 .
. -
(iii)
Repeat the previous step for all the range bins. Subsequently, construct the superresolution ISAR image
 , where
, where  indicates the number of Doppler bin.
indicates the number of Doppler bin.
The algorithm is schematically shown in the flowchart depicted in Figure 3, where the acronym SRA refers to superresolution algorithm.
Take into account that SRA may apply to the AR, MUSIC, or Capon spectral estimators, on which the paper concentrates. For completeness, in the next subsections, a brief description of these spectral estimators is provided.
3.1. Spectral Estimation Based on AR Coefficients
In this superresolution technique, it is assumed that the data are the output of an Infinite Impulse Response (IIR) filter, whose input is excited with a white noise of variance  [18]. If the signal is represented as
[18]. If the signal is represented as  , then it can be expressed as the filter output as
, then it can be expressed as the filter output as

where  are the filter coefficients,
are the filter coefficients,  is the filter order, and
is the filter order, and  is the white noise at the input.
is the white noise at the input.
The spectral estimator based on AR coefficients as a function of the frequency  for the signal
for the signal  may be written as [18]
may be written as [18]

where  indicates conjugate transpose,
indicates conjugate transpose,  is the sampling frequency, and
is the sampling frequency, and

Some methods to calculate the filter coefficients  and the variance of the white noise
and the variance of the white noise  have been proposed [18]. Note that these values are necessary to evaluate (7). In this paper, we have used the modified variance method, which minimizes the forward and backward prediction errors [18].
have been proposed [18]. Note that these values are necessary to evaluate (7). In this paper, we have used the modified variance method, which minimizes the forward and backward prediction errors [18].
3.2. Spectral Estimation Based on MUSIC
The MUSIC estimator is also a parametric approach which supposes that the signal is a combination of sinusoids contaminated with white noise [19]. The MUSIC spectral estimator as a function of the frequency  for the signal
for the signal  is [19]
is [19]

where  is the
is the  th eigenvector of the correlation matrix
th eigenvector of the correlation matrix  (of dimensions
(of dimensions  ) of the input signal
) of the input signal  . The eigenvectors
. The eigenvectors  are ordered according to their corresponding eigenvalues
are ordered according to their corresponding eigenvalues  , in such a way that the first
, in such a way that the first  eigenvectors generate the signal subspace and the rest generate the noise subspace. Moreover, the vector
eigenvectors generate the signal subspace and the rest generate the noise subspace. Moreover, the vector  in (9) can be written as
in (9) can be written as

For the determination of  , the extended criterion of Akaike may be employed [18]. If
, the extended criterion of Akaike may be employed [18]. If  , the function in (11) is calculated for each
, the function in (11) is calculated for each  :
:

The estimated number of sinusoids N s is the value of q which minimizes expression (11).
3.3. Capon Spectral Estimation
Finally, the Capon spectral estimator for the signal  , can be written in a similar way to MUSIC as [20]
, can be written in a similar way to MUSIC as [20]

where  is the vector provided by (10) and
is the vector provided by (10) and  is the correlation matrix (of dimensions
is the correlation matrix (of dimensions  ) of the input signal
) of the input signal  .
.
4. Comparison Results for Simulated Data
In this section, simulated data have been used to make the pertinent comparisons between the technique based on superresolution methods and the motion compensation-based approaches. These data have extensively been used in the literature to compare different ISAR focusing methods [37]. The data belong to a simulated MIG-25 aircraft, which is composed of 120 scatterers. The target is uniformly rotating, whereas a high-resolution radar illuminates it. The radar parameters are detailed in Table 1.
Figure 4 shows the ISAR image obtained after applying the standard RDA for the entire CPI. Clearly, this ISAR image is blurred. Certainly, because of the long processed illumination interval, the target scatterers have migrated of resolution cells.
If the processed illumination interval CPI is reduced, the obtained ISAR image (by using RDA) does not suffer from cell migrations, as shown in Figure 5 for a reduced CPI of 0.137 s (i.e., by considering only 32 bursts). However, as expected, the Doppler resolution has been decreased and the image quality is poor.
Figures 6–8 show the ISAR images obtained with the method based on superresolution algorithms, when the reduced CPI of 0.137 s is considered. Figure 6 presents the result when the spectral estimator based on AR coefficients is used, whereas Figures 7 and 8 refer to the result when using the MUSIC and Capon estimators, respectively. For the AR coefficients, a filter order of  has been considered. For the results provided by the MUSIC and Capon spectral estimators, a matrix dimension of
has been considered. For the results provided by the MUSIC and Capon spectral estimators, a matrix dimension of  has been considered for the correlation matrix.
has been considered for the correlation matrix.
Finally, Figure 9 presents the ISAR image obtained after compensating the motion for the entire CPI. For this purpose, the techniques in [26, 28, 36] have been applied. Note that the target scatterers are clearly distinguishable in this result. The ISAR image in Figure 9 is highly focused.
As commented in the introduction, the entropy and the contrast are focusing indicators extensively used in the literature [28, 30]. Their expressions may, respectively, be written as


where  is the ISAR image,
is the ISAR image,  calculates the sample mean,
calculates the sample mean,  is the number of range bin,
is the number of range bin,  is the number of Doppler bin, and
is the number of Doppler bin, and  is given by
is given by

In the literature, it is assumed that the greater the contrast and the lower the entropy are, the more focused the ISAR images are [28, 30]. This is usually valid to make comparisons among different autofocusing methods. However, as shown next, the entropy and the contrast are not proper focusing indicators to measure the image quality of the ISAR images obtained by using a superresolution-based technique.
The contrast and the entropy for the ISAR images depicted in Figures 4–9 are detailed in Table 2.
By carefully analyzing the results provided in this section, we may draw the next conclusions.
-
(i)
The ISAR images obtained by applying the technique based on superresolution algorithms usually present spurious scatterers; that is, they have peaks whose positions do not correspond with locations of real scatterers. We attribute this behavior to the fact that the inherent parametric model assumed by the superresolution techniques may not adequately adjust to the ISAR data. Note that the ISAR data are complex; as an example, take into account that interference among scatterers is always present in complex targets.
-
(ii)
Hence, the qualitative appearance of the ISAR images obtained with the superresolution-based approach is not satisfactory. Their quality may be greater than the RDA-based images (Figures 4 and 5), but it is clear that the superresolution-based approach does not outperform the motion compensation-based results (Figure 9), where the scatterers are clearly visible and localizable. Possible subsequent ATR algorithms may have problems with the spurious peaks appearing in the superresolution-based ISAR images.
-
(iii)
By comparing the results provided by the AR, MUSIC, and Capon spectral estimators, the most promising output is the one given by the Capon estimator, since the target contour is more detailed. On the other hand, it is clear that, for complex radar data, the Akaike criterion misestimates the number of sinusoids existent in each range bin.
-
(iv)
From a direct reading of Table 2, one may conclude that the images obtained with the superresolution-based technique are highly focused, because they have high contrast and low entropy values. However, according to the previous conclusions, we know that the superresolution approaches do not outperform the motion compensation-based techniques. The explanation for the high contrast and low entropy values must be found in the very abrupt peaks generated by the parametric approaches [18]. We admit that these focusing indicators are really useful for other ISAR contexts [28, 30], but we also conclude that they are useless for assessing the performance of ISAR focusing superresolution-based approaches.
5. Comparison Results for Real Data
In this paper, we also present the results of applying the commented algorithms to real data in order to verify that the previously drawn conclusions are still valid for live scenarios. The data belong to a sailboat, which was illuminated by a millimeter-wave high-resolution radar [38]. The radar parameters are detailed in Table 3.
Figure 10 shows the ISAR image obtained after using RDA for the entire CPI. Because of the large CPI, the ISAR image is blurred. Figure 11 presents the ISAR image (by using RDA) for a reduced CPI of 0.064 s. This image has a poor Doppler resolution, as expected.
Figures 12–14 show the ISAR images obtained after applying the superresolution technique based on the AR, MUSIC, and Capon estimators, respectively. For the AR coefficients, a filter order of  has been considered. On the other hand, for the MUSIC and Capon spectral estimators, a matrix dimension of
has been considered. On the other hand, for the MUSIC and Capon spectral estimators, a matrix dimension of  has been considered for the correlation matrix.
has been considered for the correlation matrix.
Finally, Figure 15 shows the ISAR image obtained after compensating the motion for the entire CPI. This image is highly detailed and may be useful for subsequent recognition/identification algorithms. A photo of the sailboat is also included in Figure 15 for reference.
The contrast and the entropy for the real ISAR images in Figures 10–15 are detailed in Table 4. Again, high contrast and low entropy values are obtained for the superresolution-based ISAR images.
The results obtained with real data are analogous to the ones achieved with simulated data. Consequently, the conclusions drawn at the end of Section 4 are also applicable to the real data detailed in this section.
6. Conclusions
The ISAR technique is a radar imaging method which may be very interesting in defense and security applications. In fact, ISAR can provide images of noncooperative targets in adverse meteorological conditions and in degraded scenarios.
Generally, it is interesting to process long illumination intervals to guarantee a high Doppler resolution. In this case, it is almost mandatory to apply motion compensation techniques, if focused ISAR images are desired. Otherwise, the radar images are highly blurred and are useless for recognition/identification purposes.
On the other hand, if the processed CPI is reduced, the target scatterers do not migrate of resolution cells and their associated Doppler frequencies may be considered to be constant. In this case, the ISAR images have a poor Doppler resolution, which may theoretically be improved by using superresolution algorithms.
In this paper, we have concentrated on the comparison between the superresolution-based approaches and the motion compensation-based methods with respect to their capabilities of focusing ISAR images. Both simulated and real data from complex targets have been used.
Our main conclusion is that motion compensation cannot be circumvented, that is, it is always necessary to compensate the motion, if focused high-resolution ISAR images are desired. The ISAR images obtained after applying superresolution approaches usually present spurious peaks, whose positions do not correspond to locations of real scatterers. These images could not be properly exploited by subsequent ATR algorithms.
The paper also provides the values of the entropy and the contrast for all the presented ISAR images. The superresolution-based images have high contrast and low entropy values, but this is not indicative of an increase in image quality.
References
Chen C-C, Andrews HC: Target motion induced radar imaging. IEEE Transactions on Aerospace and Electronic Systems 1980, 16(1):2-14.
Ausherman DA, Kozma A, Walker JL, Jones HM, Poggio EC: Developments in radar imaging. IEEE Transactions on Aerospace and Electronic Systems 1984, 20(4):363-400.
Carrara WG, Goodman RS, Majewski RM: Spotlight Synthetic Aperture Radar. Signal Processing Algorithms. Artech House, Boston, Mass, USA; 1995.
Hovanessian SA: Introduction to Sensor Systems. Artech House, Boston, Mass, USA; 1988.
Jelalian AV: Laser Radar Systems. Artech House, Boston, Mass, USA; 1992.
Osche GR, Young DS: Imaging laser radar in the near and far infrared. Proceedings of the IEEE 1996, 84(2):103-125. 10.1109/5.482225
Kim K-T, Seo D-K, Kim H-T: Efficient classification of ISAR images. IEEE Transactions on Antennas and Propagation 2005, 53(5):1611-1621.
Kumar BKS, Prabhakar B, Suryanarayana K, Thilagavathi V, Rajagopal R: Target identification using harmonic wavelet based ISAR imaging. EURASIP Journal on Applied Signal Processing 2006, 2006:-13.
Radoi E, Quinquis A, Totir F: Supervised self-organizing classification of superresolution ISAR images: an anechoic chamber experiment. EURASIP Journal on Applied Signal Processing 2006, 2006:-14.
Musman S, Kerr D, Bachmann C: Automatic recognition of ISAR ship images. IEEE Transactions on Aerospace and Electronic Systems 1996, 32(4):1392-1404. 10.1109/7.543860
Wehner DR: High Resolution Radar. 2nd edition. Artech House, Boston, Mass, USA; 1995.
Nuthalapati RM: High resolution reconstruction of ISAR images. IEEE Transactions on Aerospace and Electronic Systems 1992, 28(2):462-472. 10.1109/7.144572
Odendaal JW, Barnard E, Pistorius CWI: Two-dimensional superresolution radar imaging using the MUSIC algorithm. IEEE Transactions on Antennas and Propagation 1994, 42(10):1386-1391. 10.1109/8.320744
Wu R, Liu Z-S, Li J: Time-varying complex spectral analysis via recursive APES. IEE Proceedings on Radar, Sonar and Navigation 1998, 145(6):354-360. 10.1049/ip-rsn:19982435
Kim K-T, Kim S-W, Kim H-T: Two-dimensional ISAR imaging using full polarisation and superresolution processing techniques. IEE Proceedings on Radar, Sonar and Navigation 1998, 145(4):240-246. 10.1049/ip-rsn:19982033
Liu Z-S, Wu R, Li J: Complex ISAR imaging of maneuvering targets via the Capon estimator. IEEE Transactions on Signal Processing 1999, 47(5):1262-1271. 10.1109/78.757214
Quinquis A, Radoi E, Totir F-C: Some radar imagery results using superresolution techniques. IEEE Transactions on Antennas and Propagation 2004, 52(5):1230-1244. 10.1109/TAP.2004.827541
Marple SL Jr.: Digital Spectral Analysis with Applications. Prentice Hall, Englewood Cliffs, NJ, USA; 1987.
Schmidt RO: Multiple emitter location and signal parameter estimation. IEEE Transactions on Antennas and Propagation 1986, 34(3):276-280. 10.1109/TAP.1986.1143830
Capon J: High-resolution frequency-wavenumber spectrum analysis. Proceedings of the IEEE 1969, 57(8):1408-1418.
Chen VC: Time-Frequency Transforms for Radar Imaging and Signal Analysis. Artech House, Boston, Mass, USA; 2002.
Chen VC, Miceli WJ: Simulation of ISAR imaging of moving targets. IEE Proceedings on Radar, Sonar and Navigation 2001, 148(3):160-166. 10.1049/ip-rsn:20010384
Walker JL: Range-Doppler imaging of rotating objects. IEEE Transactions on Aerospace and Electronic Systems 1980, 16(1):23-52.
Delisle GY, Wu H: Moving target imaging and trajectory computation using ISAR. IEEE Transactions on Aerospace and Electronic Systems 1994, 30(3):887-899. 10.1109/7.303757
Wang J, Kasilingam D: Global range alignment for ISAR. IEEE Transactions on Aerospace and Electronic Systems 2003, 39(1):351-357. 10.1109/TAES.2003.1188917
Muñoz-Ferreras JM, Pérez-Martínez F: Extended envelope correlation for range bin alignment in ISAR. Proceedings of the IET International Conference on Radar Systems (RADAR '07), October 2007, Edinburg, UK 65-68.
Zhu D, Wang L, Yu Y, Tao Q, Zhu Z: Robust ISAR range alignment via minimizing the entropy of the average range profile. IEEE Geoscience and Remote Sensing Letters 2009, 6(2):204-208.
Xi LI, Liu G, Ni J: Autofocusing of ISAR images based on entropy minimization. IEEE Transactions on Aerospace and Electronic Systems 1999, 35(4):1240-1252. 10.1109/7.805442
Steinberg BD: Microwave imaging of aircraft. Proceedings of the IEEE 1988, 76(12):1578-1592. 10.1109/5.16351
Martorella M, Berizzi F, Haywood B: Contrast maximisation based technique for 2-D ISAR autofocusing. IEE Proceedings on Radar, Sonar and Navigation 2005, 152(4):253-262. 10.1049/ip-rsn:20045123
Wahl DE, Eichel PH, Ghiglia DC, Jakowatz CV Jr.: Phase gradient autofocus—a robust tool for high resolution SAR phase correction. IEEE Transactions on Aerospace and Electronic Systems 1994, 30(3):827-835. 10.1109/7.303752
Lipps R, Kerr D: Polar reformatting for ISAR imaging. Proceedings of the IEEE National Radar Conference, May 1998, Dallas, Tex, USA 275-280.
Werness SAS, Carrara WG, Joyce LS, Franczak DB: Moving target imaging algorithm for SAR data. IEEE Transactions on Aerospace and Electronic Systems 1990, 26(1):57-67. 10.1109/7.53413
Aprile A, Mauri A, Pastina D: Real time rotational motion compensation algorithm for focusing spot-SAR/ISAR images in case of variable rotation-rate. Proceedings of the 1st European Radar Conference (EURAD '04), October 2004, Amsterdam, The Netherlands 141-144.
Xing M, Wu R, Bao Z: High resolution ISAR imaging of high speed moving targets. IEE Proceedings on Radar, Sonar and Navigation 2005, 152(2):58-67. 10.1049/ip-rsn:20045084
Muñoz-Ferreras JM, Pérez-Martínez F: Uniform rotational motion compensation for inverse synthetic aperture radar with non-cooperative targets. IET Radar, Sonar and Navigation 2008, 2(1):25-34. 10.1049/iet-rsn:20060170
Chen VC1999, http://airborne.nrl.navy.mil/~vchen/tftsa.html
Blanco-del-Campo A, Asensio-López A, Dorta-Naranjo BP, et al.: Millimeter-wave radar demonstrator for high resolution imaging. Proceedings of the 1st European Radar Conference (EURAD '04), October 2004, Amsterdam, The Netherlands 65-68.
Acknowledgments
This work was financially supported by the Spanish National Board of Scientific and Technology Research under Project TEC2008-02148/TEC. The authors thank Dr. A. Blanco-del-Campo, Dr. A. Asensio-López, and Dr. B. P. Dorta-Naranjo for providing the live data of the sailboat.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Muñoz-Ferreras, J.M., Pérez-Martínez, F. Superresolution versus Motion Compensation-Based Techniques for Radar Imaging Defense Applications. EURASIP J. Adv. Signal Process. 2010, 308379 (2010). https://doi.org/10.1155/2010/308379
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/308379
 , where
, where 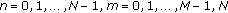 is the number of range bins, and
is the number of range bins, and 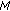 is the total number of acquired range profiles. Hence, the columns of
is the total number of acquired range profiles. Hence, the columns of 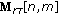 are the range profiles.
are the range profiles. . The resulting matrix
. The resulting matrix 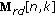 is the ISAR image generated by using RDA.
is the ISAR image generated by using RDA.

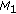 of range profiles of
of range profiles of 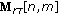 . This is equivalent to reducing the CPI. This simplified set may mathematically be expressed as
. This is equivalent to reducing the CPI. This simplified set may mathematically be expressed as 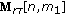 , where
, where 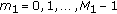 , with
, with 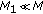 . The selection of
. The selection of 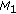 depends on the target dynamics.
depends on the target dynamics. th range bin, estimate its high-resolution frequency content by applying a superresolution algorithm. That is, apply a superresolution technique to each row of
th range bin, estimate its high-resolution frequency content by applying a superresolution algorithm. That is, apply a superresolution technique to each row of 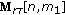 .
. , where
, where  indicates the number of Doppler bin.
indicates the number of Doppler bin.











