- Research Article
- Open access
- Published:
A New Bigram-PLSA Language Model for Speech Recognition
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 308437 (2010)
Abstract
A novel method for combining bigram model and Probabilistic Latent Semantic Analysis (PLSA) is introduced for language modeling. The motivation behind this idea is the relaxation of the "bag of words" assumption fundamentally present in latent topic models including the PLSA model. An EM-based parameter estimation technique for the proposed model is presented in this paper. Previous attempts to incorporate word order in the PLSA model are surveyed and compared with our new proposed model both in theory and by experimental evaluation. Perplexity measure is employed to compare the effectiveness of recently introduced models with the new proposed model. Furthermore, experiments are designed and carried out on continuous speech recognition (CSR) tasks using word error rate (WER) as the evaluation criterion. The superiority of the new bigram-PLSA model over Nie et al.'s bigram-PLSA and simple PLSA models is demonstrated in the results of our experiments. Experiments on BLLIP WSJ corpus show about 12% reduction in perplexity and 2.8% WER improvement compared to Nie et al.'s bigram-PLSA model.
1. Introduction
Language models are important in various applications especially in speech recognition. Statistical language models are obtained using different approaches depending on the resources and tasks requirements. Extracting  -gram statistics is a prevalent approach for statistical language modeling.
-gram statistics is a prevalent approach for statistical language modeling.  -gram takes the order of words into account and calculates the probability of the word occurring after
-gram takes the order of words into account and calculates the probability of the word occurring after  other known words.
other known words.
Many attempts have been made to incorporate semantic knowledge in language modeling. Latent topic modeling approaches such as Latent Semantic Analysis (LSA) [1, 2], Probabilistic Latent Semantic Analysis (PLSA) [3], and Latent Dirichlet Allocation (LDA) [4] are the most recent techniques. Latent semantic information is extracted by these models through decomposing word-document cooccurrence matrix. These topic models have been successful in reducing the perplexity and improving the accuracy rate of speech recognition systems [2, 5, 6]. The main deficiency of the topic models is that they do not take the order of words into consideration due to the assumption of "bag of words" intrinsically.
The useful semantic modeling of the topic models and the potential of considering words history in the  -gram language model motivate researchers to combine the capabilities of both approaches. Bellegarda [2] proposed the combination of the
-gram language model motivate researchers to combine the capabilities of both approaches. Bellegarda [2] proposed the combination of the  -gram and the LSA models and Federico [7] utilized the PLSA framework to adapt the
-gram and the LSA models and Federico [7] utilized the PLSA framework to adapt the  -gram language model. Both [2, 7] used rescaling approach for the combination. Griffiths et al. [8] presented an extension of the topic model that is sensitive to word order and automatically learns the syntactic factors as well as the semantic ones. In [9, 10] the collocation of words was incorporated in the LDA model. Girolami and Kaban [11] relaxed the "bag of words" assumption in the LDA model by applying the Markov chain assumption on symbol sequences. Wallach [12] proposed a combination of bigram and LDA models (the bigram topic model) and achieved a significant performance improvement on perplexity by exploring latent semantics following different context words. This research was a basis for Nie et al.'s work [13] that proposed the combination of bigram and PLSA models. The performance improvements achieved in [12, 13] motivated us to propose a general framework for combining bigram and PLSA models. As discussed in Section 3.6, our model is different from Nie et al.'s work and can be considered as a generalization to that model. One cannot derive the re-estimation formulae via the standard EM procedure based on Nie et al.'s model. In this paper, we propose an EM procedure for re-estimating the parameters of our model.
-gram language model. Both [2, 7] used rescaling approach for the combination. Griffiths et al. [8] presented an extension of the topic model that is sensitive to word order and automatically learns the syntactic factors as well as the semantic ones. In [9, 10] the collocation of words was incorporated in the LDA model. Girolami and Kaban [11] relaxed the "bag of words" assumption in the LDA model by applying the Markov chain assumption on symbol sequences. Wallach [12] proposed a combination of bigram and LDA models (the bigram topic model) and achieved a significant performance improvement on perplexity by exploring latent semantics following different context words. This research was a basis for Nie et al.'s work [13] that proposed the combination of bigram and PLSA models. The performance improvements achieved in [12, 13] motivated us to propose a general framework for combining bigram and PLSA models. As discussed in Section 3.6, our model is different from Nie et al.'s work and can be considered as a generalization to that model. One cannot derive the re-estimation formulae via the standard EM procedure based on Nie et al.'s model. In this paper, we propose an EM procedure for re-estimating the parameters of our model.
The remainder of the paper is organized as follows. In Section 2, the PLSA model is briefly reviewed. In Section 3, the combination of bigram and PLSA models is introduced and its parameter estimation procedure is described. In Section 4, experimental results are presented and finally in Section 5 the conclusions are made.
2. Review of the PLSA Model
Suppose that we have a set of words  that composes a set of documents
that composes a set of documents  . In the PLSA model, the occurrence probability of word w
i
given document d
j
is defined as below [3].
. In the PLSA model, the occurrence probability of word w
i
given document d
j
is defined as below [3].

where  is a latent class variable (or a topic) belonging to a set of class variables (topics)
is a latent class variable (or a topic) belonging to a set of class variables (topics)  . Equation (1) is a weighted mixture of word distributions called aspect model [14]. The aspect model is a latent variable model for co-occurrence data that associates an unobserved class variable
. Equation (1) is a weighted mixture of word distributions called aspect model [14]. The aspect model is a latent variable model for co-occurrence data that associates an unobserved class variable  to each observation (i.e., words and documents). The aspect model introduces a conditional independence assumption, that is, d
j
and w
i
are independent conditioned on the state of the associated latent variable [15]. In (1),
to each observation (i.e., words and documents). The aspect model introduces a conditional independence assumption, that is, d
j
and w
i
are independent conditioned on the state of the associated latent variable [15]. In (1),  ,
,  ,
,  are the word distributions and
are the word distributions and  ,
,  ,
,  are the weights of distributions.
are the weights of distributions.
In another view, the PLSA model is a decomposition of word-document co-occurrence matrix  . The
. The  matrix is decomposed into
matrix is decomposed into  and
and  matrices in order to minimize the cross entropy (KL divergence) between the
matrices in order to minimize the cross entropy (KL divergence) between the  matrix and empirical distribution.
matrix and empirical distribution.
The PLSA parameters  and
and  are re-estimated via the EM procedure. The EM procedure includes two alternate steps: (i) an expectation (E) step where posterior probabilities are computed for the latent variables based on the current estimates of the parameters, (ii) a maximization (M) step where PLSA parameters are updated based on the posterior probabilities computed in the E-step [15].
are re-estimated via the EM procedure. The EM procedure includes two alternate steps: (i) an expectation (E) step where posterior probabilities are computed for the latent variables based on the current estimates of the parameters, (ii) a maximization (M) step where PLSA parameters are updated based on the posterior probabilities computed in the E-step [15].
3. Combining Bigram and PLSA Models
Before describing the proposed model, the previous research on combining bigram and PLSA model by Nie et al. [13] is reviewed. This method is a special case (with certain independence assumptions) of our proposed method.
3.1. Nie et al.'s Bigram-PLSA Model
Nie et al. presented a combination of bigram and PLSA models [13]. Instead of  in (1), their bigram-PLSA model employs
in (1), their bigram-PLSA model employs  resulting in
resulting in

The EM procedure for training the combined model contains the following two steps.
E-step:

M-step:


where  is the number of times that the word pair
is the number of times that the word pair  occurs in the document d
k
, and
occurs in the document d
k
, and  is the number of words in the document d
k
.
is the number of words in the document d
k
.
3.2. Proposed Bigram-PLSA Model
We intend to combine the bigram and the PLSA models to take advantage of the strengths of both models for increasing the predictability of words in documents. In order to combine bigram and PLSA models, we incorporate the context word  in the PLSA parameters. In other words, we associate the generation of words and documents to the context word in addition to the latent topics.
in the PLSA parameters. In other words, we associate the generation of words and documents to the context word in addition to the latent topics.
The generative process of bigram-PLSA model can be defined by the following scheme:
-
(1)
Generate a context word
 as the word history with probability
as the word history with probability  .
. -
(2)
Select a document d k with probability
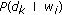 .
. -
(3)
Pick a latent variable z l with probability
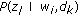 .
. -
(4)
Generate a word w j with probability
 .
.
Translating the generative process into a joint probability model results in

According to (6), the occurrence probability of the word w
j
given the document d
k
and the word history  is defined as
is defined as

Equation (7) is an extended version of the aspect model that considers the word history in the word-document modeling and can be considered as a combination of bigram and PLSA models. In (7), the distributions  and
and  are the model parameters that should be estimated from training data. This model is similar to the original PLSA model except that the context words (word history)
are the model parameters that should be estimated from training data. This model is similar to the original PLSA model except that the context words (word history)  is incorporated in the model parameters.
is incorporated in the model parameters.
Like the original aspect model, the extended aspect model assumes conditional independence between word w
j
and document d
k
, that is, w
j
and d
k
are independent conditioned on the latent parameter z
l
and the context word  :
:

The justification behind the assumed conditional independence in the proposed model is the same reasoning that the PLSA model is using to make an analytical model, that is, simplification of the model formulation and reasonable reduction of the computational cost.
As in the original PLSA model, the equivalent parameterization of the joint probability in (6) can be written as

3.3. Parameter Estimation Using the EM Algorithm
Like original PLSA model, we re-estimate the parameters of bigram-PLSA model using the EM procedure. In the EM procedure, for E-step, we simply apply Bayes' rule to obtain the posterior probability of the latent variable z
l
given the observed data d
k
,  , and w
j
.
, and w
j
.
E-step:

We can rewrite (10) as

In the M-step, the parameters are updated by maximizing the log-likelihood of the complete data (words and documents) with respect to the probabilistic model. The likelihood of the complete data with respect to the probabilistic model is computed as

where  is the occurrence probability of the word pair
is the occurrence probability of the word pair  in the document
in the document  and
and  is the frequency of word pair
is the frequency of word pair  in the document
in the document  .
.
Let  be the set of model parameters. For estimating
be the set of model parameters. For estimating  , we use MLE to maximize the log-likelihood of the complete data:
, we use MLE to maximize the log-likelihood of the complete data:

Considering (7), we expand the above equation to

In (14), the left factor before the plus sign is omitted because it is independent of  . In order to maximize the log-likelihood, (14) should be differentiated. Differentiating (14) with respect to the parameters does not lead to well-formed formulae, so we try to find a lower bound for (14) using Jensen's inequality
. In order to maximize the log-likelihood, (14) should be differentiated. Differentiating (14) with respect to the parameters does not lead to well-formed formulae, so we try to find a lower bound for (14) using Jensen's inequality

The obtained lower bound should be maximized, that is, maximizing the right hand side of (15) instead of its left hand side. For maximizing the lower bound and re-estimating the parameters, we have a constrained optimization problem because all parameters indicate probability distributions. Therefore, the parameters should satisfy the constraints

In order to consider the above constraints, the right hand side of (15) has to be augmented by the appropriate Lagrange multipliers

where  and
and  are the Lagrange multipliers related to constraints specified in (16).
are the Lagrange multipliers related to constraints specified in (16).
Differentiating the above equation partially with respect to the different parameters leads to(18)

Solving (18) and applying the constraints (16), the M-step re-estimation formulae, (19), are obtained:

The E-step and M-step are repeated until convergence criterion is met.
3.4. Implementation and Complexity Analysis
For implementing the EM algorithm, in the E-step, we need to calculate  for all i, j, k, and l. It requires four nested loops. Thus the time complexity of the E-step is
for all i, j, k, and l. It requires four nested loops. Thus the time complexity of the E-step is  , where M, N, and K are the number of words, the number of documents, and the number of latent topics respectively. The memory requirements in the E-step include a four-dimensional matrix for saving
, where M, N, and K are the number of words, the number of documents, and the number of latent topics respectively. The memory requirements in the E-step include a four-dimensional matrix for saving  and a three-dimensional matrix for saving the normalization parameter (denominator of (11)). For reducing the memory requirements, note that it is not necessary to calculate and save
and a three-dimensional matrix for saving the normalization parameter (denominator of (11)). For reducing the memory requirements, note that it is not necessary to calculate and save  at the E-step; rather, it can be calculated in the M-step by multiplying the previous
at the E-step; rather, it can be calculated in the M-step by multiplying the previous  and
and  and dividing the result by the normalization parameter. Therefore, we save only the normalization parameter at the E-step. According to (7), the normalization parameter is equal to
and dividing the result by the normalization parameter. Therefore, we save only the normalization parameter at the E-step. According to (7), the normalization parameter is equal to  , thus the related matrix contains
, thus the related matrix contains  elements, which is a large number for typical values of M and N.
elements, which is a large number for typical values of M and N.
In the M-step, we need to calculate the model parameters  and
and  specified in (19). These calculations require four nested loops, but note that we can decrease the number of loops to three nested loops by considering only the word pairs that are present in the training documents instead of all word pairs. Thus the time complexity in the M-step is O(KNB) where B is the average number of the word pairs in the training documents.
specified in (19). These calculations require four nested loops, but note that we can decrease the number of loops to three nested loops by considering only the word pairs that are present in the training documents instead of all word pairs. Thus the time complexity in the M-step is O(KNB) where B is the average number of the word pairs in the training documents.
The memory requirements in the M-step include two three-dimensional matrices for saving  and
and  and two two-dimensional matrices for saving the denominators of (19). Saving these large matrices results in high memory requirements in the training process.
and two two-dimensional matrices for saving the denominators of (19). Saving these large matrices results in high memory requirements in the training process.  is another matrix that can be implemented by a sparse matrix containing the indices of the word pairs presented in each training document and the counts of the word pairs.
is another matrix that can be implemented by a sparse matrix containing the indices of the word pairs presented in each training document and the counts of the word pairs.
3.5. Extension to  -gram
-gram
We can extend the bigram-PLSA model to  -gram-PLSA model by considering the
-gram-PLSA model by considering the  context words
context words  instead of only one context word w
i
as the word history. The generative process of the
instead of only one context word w
i
as the word history. The generative process of the  -gram-PLSA model is similar to the bigram-PLSA model except that in step 1, instead of generating one context word,
-gram-PLSA model is similar to the bigram-PLSA model except that in step 1, instead of generating one context word,  context words should be generated. Therefore, the combined model can be expressed by
context words should be generated. Therefore, the combined model can be expressed by

where  is a sequence of
is a sequence of  words. We can follow the same EM procedure for parameter estimation in the
words. We can follow the same EM procedure for parameter estimation in the  -gram-PLSA model where w
i
is replaced by
-gram-PLSA model where w
i
is replaced by  in all formulae. In the re-estimation formulae, we have
in all formulae. In the re-estimation formulae, we have  that is the number of occurrences of the word sequence
that is the number of occurrences of the word sequence  in the document d
k
.
in the document d
k
.
Combining PLSA model and  -gram model for
-gram model for  leads to high complexity in time and memory of the training process. As discussed in Section 3.4, the time complexity of the EM algorithm is
leads to high complexity in time and memory of the training process. As discussed in Section 3.4, the time complexity of the EM algorithm is  for
for  . Consequently, the time complexity for higher order
. Consequently, the time complexity for higher order  -grams is
-grams is  that grows exponentially as n increases. In addition, the memory requirement for
that grows exponentially as n increases. In addition, the memory requirement for  -gram-PLSA combination is very high. For example, for saving the normalization parameters, we need a (
-gram-PLSA combination is very high. For example, for saving the normalization parameters, we need a ( )-dimensional matrix which contains
)-dimensional matrix which contains  elements. Therefore, the memory requirement also grows exponentially as n increases.
elements. Therefore, the memory requirement also grows exponentially as n increases.
3.6. Comparison with Nie et al.'s Bigram-PLSA Model
As discussed in Section 3.1, Nie et al. have presented a combination of bigram and PLSA models in 2007 [13]. This work does not have a strong mathematical foundation and one cannot derive the re-estimation formulae via the standard EM procedure based on that. Nie et al.'s work is based on an assumption of independence between the latent topics z l and the context words w i . According to this assumption, we can rewrite (7) as

According to (21), the difference between our model and Nie et al.'s model is in the definition of the topic probability. In Nie et al.'s model the topic probability is conditioned on the documents, but in our model, the topic probability is further conditioned on the bigram history. In Nie et al.'s model, the assumption of independence between the latent topics and the context words leads to assigning the latent topics to each context word evenly, that is, the same numbers of latent variables are assigned to decompose the word-document matrices of all context words despite their different complexities. Thus, they propose a refining procedure that unevenly assigns the latent topics to the context words according to an estimation of their latent semantic complexities.
In our proposed bigram-PLSA model, we relax the assumption of independence between the latent topics and the context words and achieve a general form of the aspect model that considers the word history in the word-document modeling. Our model automatically assigns the latent topics to the context words unevenly because for each context h
i
, there is a distribution  that assigns the appropriate number of latent topics to that context. Consequently,
that assigns the appropriate number of latent topics to that context. Consequently,  remains zero for those z
l
inappropriate to the context word w
i
.
remains zero for those z
l
inappropriate to the context word w
i
.
The number of free parameters in our proposed model is  , whereM, N, and K are the number of words, the number of documents, and the number latent topics, respectively. On the other hand, the number of free parameters in Nie et al.'s model is
, whereM, N, and K are the number of words, the number of documents, and the number latent topics, respectively. On the other hand, the number of free parameters in Nie et al.'s model is  that is less than the number of free parameters in our model. Consequently, the training time of Nie et al.'s model is less than the training time of our model.
that is less than the number of free parameters in our model. Consequently, the training time of Nie et al.'s model is less than the training time of our model.
4. Experimental Results
The bigram-PLSA model was evaluated using two different criteria: perplexity and word error rate of a CSR system. We selected 500 documents containing about 248600 words from BLLIP WSJ corpus and used them to train our proposed bigram-PLSA model. We replaced all stop words of the training documents with a unique symbol (#STOP) and considered all infrequent words (the words occurring only once) as unknown words and replaced them with UNK symbol. After these replacements, the vocabulary contained about 3800 words. We could not include more documents in the training process because the computational cost and memory requirement grow rapidly as the size of the training set increases (as discussed in Section 3.4). For training the bigram-PLSA model, first we set the number of the latent topics between 10 and 50 and initialized the model randomly, then we executed the EM algorithm until it converged. We evaluated the bigram-PLSA model on 50 documents, with 22300 words in total, not overlapped with the training data. This evaluation process was run ten times for different random initial models and the results were averaged.
The perplexity of evaluation data  was calculated as follows:
was calculated as follows:

where  was obtained from the value of
was obtained from the value of  in the bigram-PLSA model. Since document d was not present in the training data, we had to follow the folding-in procedure mentioned in [5] to calculate
in the bigram-PLSA model. Since document d was not present in the training data, we had to follow the folding-in procedure mentioned in [5] to calculate  . Within this procedure, the parameters
. Within this procedure, the parameters  were assumed constant and the EM algorithm was employed to calculate only
were assumed constant and the EM algorithm was employed to calculate only  parameters for
parameters for  and for those w
i
present in the document d. After convergence of the EM procedure,
and for those w
i
present in the document d. After convergence of the EM procedure,  was found. Obtained matrix
was found. Obtained matrix  contained many zero probabilities, thus we smoothed it using Witten-Bell smoothing method [16]. Note that the folding-in procedure gives the PLSA and the bigram-PLSA models an unfair advantage by allowing them to adapt the model parameters to the test data. Nevertheless, we applied it to avoid overfitting.
contained many zero probabilities, thus we smoothed it using Witten-Bell smoothing method [16]. Note that the folding-in procedure gives the PLSA and the bigram-PLSA models an unfair advantage by allowing them to adapt the model parameters to the test data. Nevertheless, we applied it to avoid overfitting.
To have a valid comparison, the PLSA and Nie et al.'s bigram-PLSA models were trained by the same data employed to train our proposed bigram-PLSA model. The folding-in procedure and Witten-Bell smoothing were also applied on the PLSA and Nie et al.'s bigram-PLSA models. Figure 1 shows the perplexities of the proposed and Nie et al.'s bigram-PLSA models for different numbers of latent topics averaged over ten times of running the experiment. In this figure, the error bars show the standard errors of the average perplexities. As seen in Figure 1, the perplexity of our proposed bigram-PLSA model is lower than the perplexity of Nie et al.'s bigram-PLSA model. The best perplexity was obtained when the number of latent topics was set to 40 in both models. Therefore, in the rest of experiments the numbers of latent topics were set accordingly.
In addition, we performed the paired t-test on the perplexity results of both methods with the significance level of 0.01. As stated, each experiment was carried out ten times. The null hypothesis is whether the average perplexities of two methods are the same. Table 1 shows the  -value obtained from the paired t-test for our experiments performed with different numbers of latent topics. The right column of Table 1 shows the
-value obtained from the paired t-test for our experiments performed with different numbers of latent topics. The right column of Table 1 shows the  -value where the alternative hypothesis is whether the average perplexity of our method is less than the average perplexity of Nie et al.'s method. All
-value where the alternative hypothesis is whether the average perplexity of our method is less than the average perplexity of Nie et al.'s method. All  -values obtained are smaller than the specified significance level. Therefore, the perplexity improvements are statistically significant.
-values obtained are smaller than the specified significance level. Therefore, the perplexity improvements are statistically significant.
 -values obtained from the pairedt-test on perplexity results of Nie et al.'s and proposed method for different numbers of latent topics (
-values obtained from the pairedt-test on perplexity results of Nie et al.'s and proposed method for different numbers of latent topics ( ).
).Table 2 shows the comparison between the average perplexities of the bigram-PLSA model and other language models. The standard errors of the average perplexities, the number of model parameters and the approximate time of each EM iteration are reported in this table. Note that the number of model parameters for the bigram and trigram language models are equal to the number of word pairs and word triplets observed in the training data, respectively. The numbers shown in Table 2 are the maximum possible number of the word pairs and triplets. In this table, the perplexities of the bigram and trigram language models, the PLSA model, and linear interpolations of the PLSA model and the bigram model are also shown. The bigram and trigram language models were trained by the training data discussed above and the Katz backoff smoothing method [17] was applied on them. Stop words and infrequent words of training data were replaced by #STOP and UNK symbols. The number of latent topics was set to 40 in the bigram-PLSA models and 50 in the PLSA model because for the PLSA model the best perplexity was obtained when the number of latent topics was set to 50. In case of linear interpolation,  in (22) was calculated as follows:
in (22) was calculated as follows:

We set  in our experiments. This value for
in our experiments. This value for  was obtained by optimizing it on the held-out data.
was obtained by optimizing it on the held-out data.
As Table 2 shows, the proposed bigram-PLSA model reduces the perplexity more than other language models; however, the number of parameters and the training time of the proposed model is more than the other models. The proposed bigram-PLSA model was incorporated in the Sphinx 4.0 [18] CSR system and thus evaluated. The SI84 part of Wall Street Journal corpus was used for training the acoustic models and the November 1992 ARPA CSR test set was used for testing. The vocabulary contained 5000 words including 3800 words used for the bigram-PLSA model, about 200 stop words and about 1000 extra words. We used a back-off trigram language model trained by the whole BLLIP WSJ corpus in the decoding process and employed the PLSA and the bigram-PLSA models for the N-best rescoring. Since the vocabulary of the bigram-PLSA model contains only 3800 content words, the stop words and the extra words existing in the N-best list were replaced by #STOP and UNK symbols, respectively. The number of candidates for N-best rescoring was set to 30 and the number of latent topics was set to 50 in the PLSA model and 40 in the bigram-PLSA models. Table 3 shows the word error rates (WERs) of the CSR system using the PLSA and the bigram-PLSA models averaged over ten runs of the experiments. In the second column of Table 3, the trigram language model was used in the decoding process while in the third column, no language model was used in the decoding process and only the PLSA-based language models were used for the N-best rescoring. The standard errors of average WERs are also given in this table.
As Table 3 shows, the PLSA and the bigram-PLSA models improve the word error rate. In addition, the word error rate obtained from the bigram-PLSA model is meaningfully lower than that of the PLSA model. Our proposed bigram-PLSA model shows slight improvement compared to Nie et al.'s bigram-PLSA model. The third column better demonstrates the effect of the bigram-PLSA model in reducing the word error rate. The average decoding time is given in the last column of Table 3. It is observed that WER is improved for the cost of increasing the decoding time, but the increase in the decoding time compared to the Nie et al.'s model is insignificant.
In addition, we performed paired t-test on WER results of the Nie et al.'s and the proposed methods. The significance level was set to be 0.01. Table 4 shows the  -values obtained from the paired t-test. As this table shows, the WER improvements are statistically significant.
-values obtained from the paired t-test. As this table shows, the WER improvements are statistically significant.
 -values obtained from the pairedt-test on WER results of Nie et al.'s and proposed method.
-values obtained from the pairedt-test on WER results of Nie et al.'s and proposed method.5. Conclusions and Future Work
In this paper, a general framework for combining bigram and PLSA models was proposed. The combined model was obtained from incorporating the word history in the PLSA parameters. Furthermore, the EM procedure for estimating the parameters of the combined model was described. Finally, the proposed model was compared to the previous work done on combining the bigram and the PLSA models by Nie et al. Our proposed model is different from Nie et al.'s model in the definition of the topic probability. In Nie et al.'s model the topic probability is conditioned on the documents, but in our model, the topic probability is further conditioned on the bigram history. The proposed model automatically assigns latent topics to each context word unevenly in contrast to the even assignment of them by Nie et al.'s initial bigram-PLSA model. We arranged experiments to evaluate our combined model based on the perplexity and the word error rate criteria. Experiments showed that our proposed bigram-PLSA model outperformed the PLSA model according to the both criteria. The proposed model also showed slight superiority over Nie et al.'s bigram-PLSA model in improving perplexity and WER. As our future research work, we intend to suggest a similar framework to combine  -gram and LDA models. We also plan to use automatic smoothing in our parameter estimation process without requiring it to be done as an extra step as it is the state-of-the-art in Bayesian machine learning methods.
-gram and LDA models. We also plan to use automatic smoothing in our parameter estimation process without requiring it to be done as an extra step as it is the state-of-the-art in Bayesian machine learning methods.
References
Deerwester S, Dumais S, Furnas G, Landauer T, Harshman R: Indexing by latent semantic analysis. Journal of the American Society of Information Science 1990, 41: 391-407. 10.1002/(SICI)1097-4571(199009)41:6<391::AID-ASI1>3.0.CO;2-9
Bellegarda JR: Exploiting latent semantic information in statistical language modeling. Proceedings of the IEEE 2000, 88(8):1279-1296. 10.1109/5.880084
Hofmann T: Probabilistic latent semantic indexing. Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, 1999, Berkeley, Calif, USA 50-57.
Blei DM, Ng AY, Jordan MI: Latent Dirichlet allocation. Journal of Machine Learning Research 2003, 3(4-5):993-1022.
Gildea D, Hofmann T: Topic-based language models using EM. Proceedings of the 6th European Conference on Speech Communication and Technology (EUROSPEECH '99), 1999, Budapest, Hungary 235-238.
Mrva D, Woodland PC: Unsupervised language model adaptation for mandarin broadcast conversation transcription. Proceedings of International Conference on Spoken Language Processing, 2006, Pittsburgh, Pa, USA 1549-1552.
Federico M: Language model adaptation through topic decomposition and MDI estimation. Proceedings of International Conference on Acoustics, Speech and Signal Processing, 2002, Orlando, Fla, USA 773-776.
Griffiths T, Steyvers M, Blei D, Tenenbaum J: Integrating topics and syntax. Advances in Neural Information Processing Systems 17, December 2004, Vancouver, Canada 87-94.
Griffiths TL, Steyvers M, Tenenbaum JB: Topics in semantic representation. Psychological Review 2007, 114(2):211-244.
Wang X, McCallum A: A note on topical n-grams. University of Massachusetts, Amherst, Mass, USA; December 2005.
Girolami M, Kaban A: Simplicial mixtures of Markov chains: distributed modeling of dynamic user profiles. In Advances in Neural Information Processing Systems 16, December 2003, Vancouver, Canada. MIT Press; 9-16.
Wallach HM: Topic modeling: beyond bag-of-words. Proceedings of the 23rd International Conference on Machine Learning (ICML '06), June 2006, Pittsburgh, Pa, USA 977-984.
Nie J, Li R, Luo D, Wu X: Refine bigram PLSA model by assigning latent topics unevenly. Proceedings of the IEEE Workshop on Automatic Speech Recognition and Understanding, 2007, Kyoto, Japan 141-146.
Hofmann T, Puzicha J, Jordan MI: Learning from dyadic data. Advances in Neural Information Processing Systems 11, November-December 1998, Denver, Colo, USA 466-472.
Hofmann T: Unsupervised learning by probabilistic latent semantic analysis. Machine Learning 2001, 42(1-2):177-196.
Witten IH, Bell TC: The zero-frequency problem: estimating the probabilities of novel events in adaptive text compression. IEEE Transactions on Information Theory 1991, 37(4):1085-1094. 10.1109/18.87000
Katz SM: Estimation of probabilities from sparse data for the language model component of speech recognizer. IEEE Transactions on Acoustics, Speech, and Signal Processing 1987, 35(3):400-401. 10.1109/TASSP.1987.1165125
Walker W, Lamere P, Kwok P, et al.: Sphinx-4: a flexible open source framework for speech recognition. SUN Microsystems; November 2004.
Acknowledgment
This paper was in part supported by a grant from Iran Telecommunication Research Center (ITRC).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bahrani, M., Sameti, H. A New Bigram-PLSA Language Model for Speech Recognition. EURASIP J. Adv. Signal Process. 2010, 308437 (2010). https://doi.org/10.1155/2010/308437
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/308437
 as the word history with probability
as the word history with probability  .
.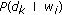 .
.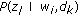 .
. .
. -gram
-gram