- Research Article
- Open access
- Published:
A Locally Adaptable Iterative RX Detector
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 341908 (2010)
Abstract
We present an unsupervised anomaly detection method for hyperspectral imagery (HSI) based on data characteristics inherit in HSI. A locally adaptive technique of iteratively refining the well-known RX detector (LAIRX) is developed. The technique is motivated by the need for better first- and second-order statistic estimation via avoidance of anomaly presence. Overall, experiments show favorable Receiver Operating Characteristic (ROC) curves when compared to a global anomaly detector based upon the Support Vector Data Description (SVDD) algorithm, the conventional RX detector, and decomposed versions of the LAIRX detector. Furthermore, the utilization of parallel and distributed processing allows fast processing time making LAIRX applicable in an operational setting.
1. Introduction
In many experiments, the RX detector is modified in a preprocessing fashion [1–10] in order to minimize the false alarm rate while attaining a reasonable true positive rate. In most cases the modifications that are proposed can be generally described as dimensionality reduction variants coupled with RX [5, 10], window adjustments for covariance estimates [2–4], and the RX detector coupled with an entropy and a nonparametric approach [1, 6]. In cases where a new anomaly detection methodology is proposed, the RX detector is often used as a performance benchmark [9, 11–14].
The literature on anomaly detection in HSI is quite extensive [1–5, 7–12, 14–18] with major contributions appearing rapidly after Reed and Yu [19, 20]. In anomaly detection, the goal has always been to distinguish background from potential targets in an automatic fashion while jointly minimizing false alarms and maximizing true positives.
The RX detector is prone to high false alarms because the local Gaussian assumption is largely inaccurate [11]. The purpose of this paper is to propose a refinement of the RX detector by taking into account the anomaly dominance upon first and second order statistic estimation. That is, we wish to force stability upon the subsequences, locally defined with respect to a window size, in order to reduce the bias and error when estimating the mean and covariance, respectively. The subsequences are refined by removing anomalies, in an iterative fashion, from consideration in local statistics estimation. Even so, the refined subsequence that is used to estimate a mean vector,  , and the covariance matrix,
, and the covariance matrix,  , is likely to still be nonGaussian; but, as is demonstrated subsequently, it often provides a better false alarm rate than the conventional RX because its estimates are not as contaminated by anomalies.
, is likely to still be nonGaussian; but, as is demonstrated subsequently, it often provides a better false alarm rate than the conventional RX because its estimates are not as contaminated by anomalies.
To illustrate the potential of this idea, consider the following "abbreviated" image created from a desert image (see Figure 1). The image is "abbreviated" in that the targets have been moved closer together than in the original image by simply eliminating columns of image pixels. This creates a situation with a very nonhomogeneous background. This small image is 63  49 pixels. A 25
49 pixels. A 25  25 window will be used in all subsequent processing. In Figure 1(a) the truth mask shows the known objects of interest. Figure 1(b) shows the RX scores for the HSI image, Figure 1(c) shows the RX scores for the 1st 10 principal components (instead of using the entire HSI data-cube), Figure 1(d) shows the output of LAIRX for 2 iterations (called LAIRX (2) in subsequent discussion), using PCA for the input. In Figures 1(b), 1(c), and 1(d) RX scores are displayed such that anomalies are expected to "fire" as bright and the background should "fire" as dark. Figure 1(b) shows that many background pixels may be declared as anomalies (depending on the threshold) for RX. Figure 1(c) shows the benefit of using principal components as input to RX. Figure 1(d) shows a large reduction in lighter pixels in the background using one iterative refinement of the covariance calculation used in RX.
25 window will be used in all subsequent processing. In Figure 1(a) the truth mask shows the known objects of interest. Figure 1(b) shows the RX scores for the HSI image, Figure 1(c) shows the RX scores for the 1st 10 principal components (instead of using the entire HSI data-cube), Figure 1(d) shows the output of LAIRX for 2 iterations (called LAIRX (2) in subsequent discussion), using PCA for the input. In Figures 1(b), 1(c), and 1(d) RX scores are displayed such that anomalies are expected to "fire" as bright and the background should "fire" as dark. Figure 1(b) shows that many background pixels may be declared as anomalies (depending on the threshold) for RX. Figure 1(c) shows the benefit of using principal components as input to RX. Figure 1(d) shows a large reduction in lighter pixels in the background using one iterative refinement of the covariance calculation used in RX.
2. Methods
The data used in our experiment are from the ARES desert and forest radiance collections. In our analysis we only consider two classes, background and certain man-made targets. The goal of our analysis is to distinguish the latter from many sources of background variation, such as brush, roads, forest, large rock formations and other natural anomalies.
2.1. Locally Adaptive Iterative RX Detector (LAIRX)
Reed and Yu derived an anomaly detector using a Generalized Likelihood Ratio Test (GLRT), which was later dubbed the RX detector [19, 20]. The detector GLRT is simplified by assuming that background pixel vectors are iid normal with estimated mean,  , and covariance matrix,
, and covariance matrix,  , that is,
, that is,

In short, an incoming pixel vector,  , is the center of a neighborhood of size
, is the center of a neighborhood of size  which is checked for irregularity via the distance formulated above. That is, the pixel vector is checked to see if it lies outside the hyper ellipse whose location and shape are determined via
which is checked for irregularity via the distance formulated above. That is, the pixel vector is checked to see if it lies outside the hyper ellipse whose location and shape are determined via and
and  , respectively. An anomalous vector is declared given that
, respectively. An anomalous vector is declared given that  , where
, where  is the
is the  th quantile of a
th quantile of a  distribution with p degrees of freedom. For more information see [18].
distribution with p degrees of freedom. For more information see [18].
The idea, following the philosophy of the RX method, is to place a window about each pixel in an image and use local image statistics to determine whether or not the point is anomalous. It is evident that such a method can suffer from at least 3 potential complications. First, the window pixel vectors are almost never statistically independent. Second, such vectors are not typically identically distributed. Further, outliers (the things we are looking for) can seriously compromise the integrity of the local statistics, particularly the estimated covariance matrix. The first and second complications are the subject of current research. In this paper, we examine the third complication. A look at outlier effects and some remedies is given in [18]. The basic approach given in this paper is laid out in [21]. Here, we propose to deal with the outlier effects in an iterative fashion. As we process the basic RX algorithm across the image, we maintain a catalog of anomalous pixels, this is the 1st iteration. Indeed, if we simply quit after processing the image once, we would have simply run the RX method. A second iteration is applied, only this time we withhold the anomalous pixels from consideration in calculating the local statistics. So long as we find new anomalies the iterations continue; otherwise, the algorithm terminates. Hence, in LAIRX we allow the RX detector to be iteratively refined with respect to the estimation of  and
and  while keeping track of detected anomalies. LAIRX has the following steps:
while keeping track of detected anomalies. LAIRX has the following steps:
Step 1.
Reduce the dimensionality to a set of  principal components via a global estimate of
principal components via a global estimate of  .
.
Step 2.
Apply the RX detector to the data matrix using a pixel process window. If this is not the 1st iteration, withhold anomalous pixels identified in the previous iteration from the local estimation of  and
and  .
.
Step 3.
Identify those RX scores that exceed  . These are referred to as anomalies. This step ends an iteration.
. These are referred to as anomalies. This step ends an iteration.
Step 4.
If the set of pixels identified as anomalies in Step 3 are identical to the set of pixels identified as anomalies in the previous iteration then go to Step 5, otherwise; return to Step 2.
Step 5.
Map detected anomalies to the image space.
Once LAIRX has terminated we are assume that the respective window sequences' anomaly indicator has converged almost surely to some target given the  cut-off. The subsequences associated with the target may or may not be Gaussian but the refined
cut-off. The subsequences associated with the target may or may not be Gaussian but the refined  and
and  estimates should result in a higher true positive rate coupled with a relatively low false alarm rate when compared to the conventional RX detector because the sequence is forced to be more iid and, hence, estimation bias is reduced. The global SVDD algorithm was chosen as a competing algorithm because of its recent promise as an efficient and powerful anomaly detector.
estimates should result in a higher true positive rate coupled with a relatively low false alarm rate when compared to the conventional RX detector because the sequence is forced to be more iid and, hence, estimation bias is reduced. The global SVDD algorithm was chosen as a competing algorithm because of its recent promise as an efficient and powerful anomaly detector.
In what follows, the LAIRX detector is compared to the SVDD algorithm, the conventional RX detector and a decomposed version of the LAIRX detector. This later comparison was made in an effort to more fully understand the performance of the LAIRX detector. Each anomaly detector was applied to four images; see Figure 2, containing multiple vehicles, varying land formations, sage brush and a road. These images vary in the difficulty they present to the algorithms as reflected in the SNR plots of Figure 3.
2.2. Parallel Implementation of LAIRX
The RX detector is naturally a computationally inefficient task since matrix inversions are required,
matrix inversions are required,  in our analysis. This computational burden was an inspiration for the application of SVDD in HSI anomaly detection [22]. However, most implementations of the RX detector are not optimized. We decided to optimize the RX algorithm via parallel and distributed processing on a dual quad-core machine. The implementation is very simple given the Matlab Parallel Computing Toolbox but is described nonetheless.
in our analysis. This computational burden was an inspiration for the application of SVDD in HSI anomaly detection [22]. However, most implementations of the RX detector are not optimized. We decided to optimize the RX algorithm via parallel and distributed processing on a dual quad-core machine. The implementation is very simple given the Matlab Parallel Computing Toolbox but is described nonetheless.
2.2.1. Basic Setup
The hyperspectral image is formulated as a data matrix where columns are wavelengths and rows are pixels, respectively. A window is moved row-wise across the data matrix at a single row increment where each center pixel serves as input to the RX detector. The data held locally in each window is used to estimate  and
and  . The components of
. The components of  and
and  are based on a set of p principal components from the wavelength bands, where
are based on a set of p principal components from the wavelength bands, where  in our analysis. The number of principal components is dependent on the data collection environment and should be determined via exploratory data analysis. From our analysis, we found that the desert radiance images required only two principal components while the forest radiance images required about ten.
in our analysis. The number of principal components is dependent on the data collection environment and should be determined via exploratory data analysis. From our analysis, we found that the desert radiance images required only two principal components while the forest radiance images required about ten.
2.2.2. Parallelization Scheme
( ) Generate all possible window indices where each column indexes a window of data. The row midpoint of these data matrices are the center pixels for that particular window. This step makes RX and LAIRX an "embarrassingly parallel" problem.
) Generate all possible window indices where each column indexes a window of data. The row midpoint of these data matrices are the center pixels for that particular window. This step makes RX and LAIRX an "embarrassingly parallel" problem.
( ) The data partitions are batched in batches of size
) The data partitions are batched in batches of size  where
where  is the number of available processor cores,
is the number of available processor cores,  in our setup.
in our setup.
( ) Each batched data partitions are processed using the RX detector simultaneously.
) Each batched data partitions are processed using the RX detector simultaneously.
( ) Results are pooled and used for subsequent analysis.
) Results are pooled and used for subsequent analysis.
2.3. Global SVDD Anomaly Detector
The Support Vector Data Description (SVDD) algorithm was originally proposed by Tax and Duin as a means for exploring one class distributions [23, 24]. The SVDD anomaly detector applied to HSI was proposed by Banerjee et al. [22]. In general, the goal of the SVDD algorithm is to find the hypersphere with minimum volume about a set of random vectors. In our case these random vectors are the background pixels with each dimension corresponding to a different spectral band, that is, for a set of pixels,  , we seek the minimum enclosing hypersphere,
, we seek the minimum enclosing hypersphere,  , that contains T. This is a constrained optimization problem stated as.
, that contains T. This is a constrained optimization problem stated as.

The center  and radius
and radius  are found by optimizing the following Lagrangian:
are found by optimizing the following Lagrangian:

The next step is to apply the kernel trick with a kernel function Φ( ), which is usually taken to be Gaussian [11, 22–24]. Once L is optimized with respect to
), which is usually taken to be Gaussian [11, 22–24]. Once L is optimized with respect to  and after incorporating the kernel function,
and after incorporating the kernel function,  , we get the following SVDD statistic [11]
, we get the following SVDD statistic [11]

where

The radial basis function (RBF) parameter σ2 controls how well the SVDD generalizes to unseen data. The choice of this parameter is driven by the data and must be chosen empirically. In our analysis,  is a pixel vector and
is a pixel vector and  is a support vector obtained via SVDD given background spectra.
is a support vector obtained via SVDD given background spectra.
For HSI anomaly detection, Banerjee et al. propose a fast global SVDD detector [11]. The algorithm that they propose is fast because it uses a small subset of the data to build the SVDD model. The algorithm is as follows:
-
(1)
Randomly select a set of
 background pixels from the training set.
background pixels from the training set. -
(2)
Estimate an optimal value for s2 using a cross-validation or minimax method given the set of background spectra.
-
(3)
Estimate the SVDD parameters
 to model the region of support for the background given a random subset of the background spectra and s2.
to model the region of support for the background given a random subset of the background spectra and s2. -
(4)
For each pixel in the data matrix perform the decision test:
-
(i)
if
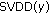 is less than the detection threshold t, the pixel is part of the background.
is less than the detection threshold t, the pixel is part of the background. -
(ii)
else, declare the pixel as an anomaly.
-
(i)
As you can see in Figure 4, there is a performance effect as σ2 is varied. The only free parameter in the RBF is σ2. We wish to find the optimal σ2 that is able to fully describe the nontarget/background spectra.
A common method is to estimate σ2 while minimizing the false positive rate (Pfa) via an argument based on leave-one-out cross validation [11, 22–25], which gives the following upper bound on Pfa:

N is the number of samples selected to train the SVDD model and #SV are the number of support vectors required to describe the data. Based upon the above inequality, Banerjee et al. [22] propose an approximate minimax estimate for σ2 as

where  is the number of replicates. Based upon the above result, the algorithm to obtain the global estimate for σ2 is the following.
is the number of replicates. Based upon the above result, the algorithm to obtain the global estimate for σ2 is the following.
-
(1)
Generate M equal sets of training data by randomly selecting pixels from the background.
-
(2)
For each set of training data, the SVDD decision boundary is determined using different values for s2.
-
(3)
For each value of
 , the average fraction of support vectors,
, the average fraction of support vectors, , is computed over all of the training sets.
, is computed over all of the training sets. -
(4)
The s2 that produces the smallest average fraction of support vectors is the minimax estimate.
We discovered that the average fraction of support vectors is at a minimum when  . Therefore, our minimax estimate is 905 because this is the smallest s2 that allows us to effectively describe our data. If
. Therefore, our minimax estimate is 905 because this is the smallest s2 that allows us to effectively describe our data. If  then our detection results may be poor because the resulting SVDD model is overly general. Note that when using the minimax approach, 60% of the training data is 300 pixel vectors while there are 149 features. The balance between sample size and number of variables is causing the minimax estimation to converge at a minimum that allows a fairly high Pfa while maintaining an effective characterization of the background spectra. This demonstrates that the bandwidth parameter selection is robust to small sample sizes relative to the number of dimensions or spectral bands.
then our detection results may be poor because the resulting SVDD model is overly general. Note that when using the minimax approach, 60% of the training data is 300 pixel vectors while there are 149 features. The balance between sample size and number of variables is causing the minimax estimation to converge at a minimum that allows a fairly high Pfa while maintaining an effective characterization of the background spectra. This demonstrates that the bandwidth parameter selection is robust to small sample sizes relative to the number of dimensions or spectral bands.
Figure 5 is SVDD pixel map with an accompanying 2D principal component scatter plots. These will contrasted in subsequent analysis.
2.4. Experiment Description
In our analysis we included all wavelength bands that were not contaminated by atmospheric absorption, which resulted in 149 bands. The global SVDD approach is supervised in the sense that it requires as input a known set of background spectra while LAIRX and RX are unsupervised. For SVDD, the sample size used when sampling from the background spectra was  . This size was chosen based upon computing limitations while accommodating the high dimensional feature space. For LAIRX, the maximum number of iterations and principal components was 50 and 10, respectively. Based on our exploratory data analysis 10 principal components was sufficient. A window size of 25
. This size was chosen based upon computing limitations while accommodating the high dimensional feature space. For LAIRX, the maximum number of iterations and principal components was 50 and 10, respectively. Based on our exploratory data analysis 10 principal components was sufficient. A window size of 25  25 was employed.
25 was employed.
Each anomaly detector was applied to four images; see Figure 2, containing multiple vehicles, varying land formations, sage brush and a road. ARES1D is desert radiance while the other three are forest radiance. Three of the images area contains less than 1% target pixels while one image has about 3.4% target pixels.
The goal of our analysis was to compare a promising anomaly detector (global SVDD), a benchmark detector (RX) and our proposal (LAIRX). The RX algorithm is run in two different modes. RX-FULL is run on the full 149 bands of the image cube; whereas, RX-PCA is run on the 10 retained principal components. Finally, in an effort to examine the iteration sensitivity of LAIRX we created a version denoted LAIRX(2) that only performs one iterative refinement (in other words, 2 RX-type iterations). In order to make inferences about these competing algorithms we investigate the runtime, percentage of target pixels, area under the ROC curve restrained to false positive cases falling below 0.20, and the true positive rate at a fixed false positive rate of 0.05. In what follows (Table 1), AUC denotes the "area under the (ROC) curve (false positive rates from 0–.2)" and TPR is the "true positive rate" at a fixed a false positive rate of 0.05.
At the onset, we believed that performance gains would be substantial given that we force our multidimensional data sequences within each window to be more iid even though these data sequences are likely to not be locally Gaussian. Even if the multivariate populations are not Gaussian, by iteratively refining the anomaly detection we are introducing robustness to our final  score map, upon which a threshold is applied to determine the final classification. A drawback to LAIRX is that you need to know a good rejection rate for the iterative refinement which is largely data dependent as you can see in Figure 6. This problem is a topic of future research.
score map, upon which a threshold is applied to determine the final classification. A drawback to LAIRX is that you need to know a good rejection rate for the iterative refinement which is largely data dependent as you can see in Figure 6. This problem is a topic of future research.
3. Results
In what follows, ROC curves are presented for each image in Figure 7 and summary statistics are offered in Table 1.
For ARES1D, the background and target pixels are linearly separable given the first and second principal components (see Figure 5(a)). Additionally, the SNR is showing a clear separation with lower SNR values present for the target pixels, which is encouraging (see Figure 5(b)). We would expect with these observations that the RX-type classifiers should do very well and that the nonlinear classifier, SVDD, should also perform reasonably well. When viewing the ROC curve for ARES1D, you can see that PCA is beneficial for the RX derivative methods. The SVDD algorithm is performing well but as you can see in the SVDD statistic map there are many locally clustered areas which display the same in value as the target pixels.
The image ARES1F poses difficulties for all the algorithms tested. ARES1F which has a very noisy SNR statistic map, as you can see in Figure 3(b). This image in particular, highlights the benefits of LAIRX's iterative approach.
The image scene is similar for both ARES2F and ARES3F (Figure 2). As you can see in Figure 3, the SNR map is showing a reasonable segmentation for both of these images and the distributions are somewhat separable. Table 1 and Figure 7 show that performance is good across the board with LAIRX being superior. It is interesting to point out that the nonlinear technique is performing poorly in contrast to the other algorithms. Additionally, the data associated with these images is separable in a lower dimensional subspace, as you can see in Figure 3, which indicates that the RX type approach should perform well. Also, note that for ARES2F and ARES3F the SVDD statistic maps depicted in Figure 5 is showing that large natural anomalies have a similar value as the targets, which leads to a higher false positive rate.
4. Discussion
We have presented an unsupervised automatic target detection algorithm which builds upon the conventional RX detector by direct manipulation of the RX algorithm. As a practical matter, the LAIRX detector must have data preprocessed as principal components before detection which hinders real-time viability while the global SVDD builds a model based upon background spectra and then classifies raw pixel vectors as anomalous as they are received. However, the global SVDD is a supervised algorithm given that a set of background spectra and RBF spread parameter are specified which may limit its real-time viability in a dynamic operational setting.
For the types of images analyzed here, our results have shown that LAIRX is a reasonable competitor to the SVDD algorithm and that a linear technique can perform well in a nonlinear environment after statistic estimation modification. We have also demonstrated, see Table 1 and Figure 7, that the algorithmic steps taken to create LAIRX interact in a way that lead to higher true positives coupled with low false positives. By introducing iterative refinement, we are getting better performance because the first and second order statistic estimation have less bias and error. Our method has demonstrated potential in an image scene with sparse vehicle activity. Whether or not similar results follow in a densely populated target environment remains to be seen.
Both LAIRX and LAIRX( ) are implemented in a parallel and distributed fashion which makes these algorithms computationally efficient. The processing time for LAIRX and LAIRX(
) are implemented in a parallel and distributed fashion which makes these algorithms computationally efficient. The processing time for LAIRX and LAIRX( ) are constrained by the number of available processor cores. In general, LAIRX is somewhat slow as you can see in Table 1 but the ready availability of cluster machines and even affordable 8 processor core machines make LAIRX a viable algorithm in an operational setting. In contrast, the runtime of the global SVDD algorithm is fixed from an algorithmic perspective of parallel and distributed computing.
) are constrained by the number of available processor cores. In general, LAIRX is somewhat slow as you can see in Table 1 but the ready availability of cluster machines and even affordable 8 processor core machines make LAIRX a viable algorithm in an operational setting. In contrast, the runtime of the global SVDD algorithm is fixed from an algorithmic perspective of parallel and distributed computing.
References
Di W, Pan Q, Zhao Y-Q, He L: Multiple-detector fusion for anomaly detection in multispectral imagery based on maximum entropy and nonparametric estimation. Proceedings of the 8th International Conference on Signal Processing (ICSP '06), January 2006 3:
Hsueh M, Chang C-I: Adaptive causal anomaly detection for hyperspectral imagery. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS ' 04), January 2004 5: 3222-3224.
Liu W, Chang C-I: A nested spatial window-based approach to target detection for hyperspectral imagery. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS '04), January 2004 5: 266-268.
Liu W, Chang C-I: Multiple-window anomaly detection for hyperspectral imagery. Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS '08), January 2008 2: 41-44.
Mei F, Zhao C, Wang L, Huo H: Anomaly detection in hyperspectral imagery based on kernel ICA feature extraction. Proceedings of the 2nd International Symposium on Intelligent Information Technology Application (IITA '08), January 2008 1: 869-873.
Mei F, Zhao C, Huo H, Sun Y: An adaptive kernel method for anomaly detection in hyperspectral imagery. Proceedings of the 2nd International Symposium on Intelligent Information Technology Application (IITA '08), January 2008 1: 874-878.
Nasrabadi NM: A nonliner kernel-based joint fusion/detection of anomalies using hyperspectral and SAR imagery. Proceedings of the IEEE International Conference on Image Processing (ICIP '08), 2008 1864-1867.
Renard N, Bourennane S: Dimensionality reduction based on tensor modeling for classification methods. IEEE Transactions on Geoscience and Remote Sensing 2009, 47(4):1123-1131.
Yanfeng G, Ye Z, Ying L: Unmixing component analysis for anomaly detection in hyperspectral imagery. Proceedings of the IEEE International Conference on Image Processing (ICIP '06), 2006 965-968.
Gu Y, Liu Y, Zhang Y: A selective kernel PCA algorithm for anomaly detection in hyperspectral imagery. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), January 2006 2: 725-728.
Banerjee A, Burlina P, Meth R: Fast hyperspectral anomaly detection via SVDD. Proceedings of the 14th IEEE International Conference on Image Processing (ICIP '07), January 2007 4: 101-104.
Gaucel J-M, Guillaume M, Bourennane S: Whitening spacial correlation filtering for hyperspectral anomaly detection. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '05), January 2005 5: 333-336.
Tiwari S, Agarwal S, Trang A: Texture feature selection for buried mine detection in airborne multispectral imagery. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS '08), 2008 1: 145-148.
Thornton SM, Moura JMF: The fully adaptive GMRF anomally detector for hyperspectral imagery. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '00), 2000 1: 37-40.
Chang C-I, Chiang S-S: Anomaly detection and classification for hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing 2002, 40(6):1314-1325. 10.1109/TGRS.2002.800280
Chang C-I, Ren H: An experiment-based quantitative and comparative analysis of target detection and image classification algorithms for hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing 2000, 38(2):1044-1063. 10.1109/36.841984
Shi M, Healey G: Using multiband correlation models for the invariant recognition of 3-D hyperspectral textures. IEEE Transactions on Geoscience and Remote Sensing 2005, 43(5):1201-1209.
Smetek TE, Bauer KW Jr.: A comparison of multivariate outlier detection methods for finding hyperspectral anomalies. Military Operations Research 2008, 13(4):19-44. 10.5711/morj.13.4.19
Reed IS, Yu X: Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Transactions on Acoustics, Speech, and Signal Processing 1990, 38(10):1760-1770. 10.1109/29.60107
Yu X, Hoff LE, Reed IS, Chen AM, Stotts LB: Automatic target detection and recognition in multiband imagery: a unified ML detection and estimation approach. IEEE Transactions on Image Processing 1997, 6(1):143-156. 10.1109/83.552103
Taitano YP: Hyperspectral imagery target detection using the iterative RX detector, M.S. thesis. School of Operation Science, Air Force Institute of Technology, Wright-Patterson AFB, Ohio, USA; March 2007. AFIT/GOR/ENS/07-25
Banerjee A, Burlina P, Diehl C: A support vector method for anomaly detection in hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing 2006, 44(8):2282-2291.
Tax DMJ, Duin RPW: Support vector domain description. Pattern Recognition Letters 1999, 20(11–13):1191-1199.
Tax DMJ, Duin RPW: Support vector data description. Machine Learning 2004, 54(1):45-66.
Vapnik VN: Statistical Learning Theory, Wiley Series on Adaptive and Learning Systems for Signal Processing, Communications, and Control. John Wiley & Sons, New York, NY, USA; 1998.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Taitano, Y.P., Geier, B.A. & Bauer, K.W. A Locally Adaptable Iterative RX Detector. EURASIP J. Adv. Signal Process. 2010, 341908 (2010). https://doi.org/10.1155/2010/341908
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/341908



 , displayed with background-target SNR histogram. (a) ARES1D, (b) ARES1F, (c) ARES2F, (d) ARES3F.
, displayed with background-target SNR histogram. (a) ARES1D, (b) ARES1F, (c) ARES2F, (d) ARES3F. background pixels from the training set.
background pixels from the training set. to model the region of support for the background given a random subset of the background spectra and s2.
to model the region of support for the background given a random subset of the background spectra and s2.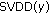 is less than the detection threshold t, the pixel is part of the background.
is less than the detection threshold t, the pixel is part of the background.
 selection for ARES1D image. Effect of bandwidth on SVDD performance. The highest performance is achieved when σ ≈ σ was incrementally varied from
selection for ARES1D image. Effect of bandwidth on SVDD performance. The highest performance is achieved when σ ≈ σ was incrementally varied from  .
. , the average fraction of support vectors,
, the average fraction of support vectors, , is computed over all of the training sets.
, is computed over all of the training sets.

