- Research Article
- Open access
- Published:
Analysis and Properties of Time-Varying Modified DFT Filter Banks
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 342865 (2010)
Abstract
We provide a comprehensive analysis of the time-varying modified DFT (MDFT) filter bank based on the general time-varying filter bank theories (Wang, 2005, 2006, 2008, 2009) in both the time domain and frequency domain. We give firstly the description of the time-invariant MDFT filter bank including its perfect reconstruction (PR) condition, its mechanism of aliasing error cancellation and the relationship with the cosine-modulated filter bank in detail. Then, the time-varying MDFT filter bank is analyzed according to the time-domain description. Finally, the window switching method is introduced to design the prototype filter in the time-varying MDFT filter bank with examples. The error analysis shows that the introduced design approach is useful in practice.
1. Introduction
Modified DFT filter banks (MDFT) and their applications are intensively studied in [1–5]. But all analyses are done in the frequency domain for the time-invariant modified DFT filter banks. In the literature, we do not find any works for the time-varying MDFT filter bank. Subband coding is a widely used method in the digital signal processing and the telecommunication areas, such as subband speech and audio coding [5–7], TDM-FDM multiplex [8], DSL communication [9], and subband adaptive filtering [10]. One of the important parts in a subband system is the analysis synthesis filter bank. The analysis filter bank is used to split the input frequency into the different subbands while the synthesis filter bank combines all subbands signals to generate a full band signal.
Among the different subband filter bank structures the modulated filter banks are most popular because of their easy design and efficient implementation. Historically, there are two classes of modulated filter banks, namely, DFT polyphase filter bank and cosine-modulated filter bank. DFT polyphase filter bank was first proposed by Bellangerr and Daguet [8]. DFT polyphase filter bank uses complex modulation. But, the original DFT polyphase filter bank does not provide the mechanism to cancel the adjacent spectrum aliasing. So, in some literatures, the DFT polyphase filter bank was considered as unsuitable for subband applications [11, 12], which also has negative effects on the further research of the DFT polyphase filter bank. To find a method to design the filter bank efficiently, in 1980s the QMF filter bank consisting of two channels and providing the almost perfect reconstruction was introduced. Later, the cosine-modulated filter banks with perfect reconstruction were introduced. Since the introduction, the cosine-modulated filter bank was widely studied and applied due to its perfect reconstruction property and the easy prototype window design with the closed formulation [12]. But, the closed prototype window formulation exists just in the case that the filter length is two times or four times of the channel length, which limits the application of the cosine-modulated filter bank. Without the closed formulation of prototype windows, it is difficult to design an applicable prototype window for a cosine-modulated filter bank to keep the perfect reconstruction property. In this case the cosine-modulated filter bank can only provide an almost perfect reconstruction similar with DFT polyphase filter bank.
In comparison with cosine-modulated filter banks, the DFT polyphase filter bank has advantages such as linear phase, complex-valued signal processing, and better frequency characteristics in each subband. Furthermore, its computational efficiency is comparable with cosine-modulated filter bank. So, if we can find an approach to efficiently cancel the aliasing error in the DFT polyphase filter bank, the DFT polyphase filter bank has good application possibilities in digital signal processing like speech and image processing. In 1990s, the good application prospects of the DFT polyphase filter bank motivate some researchers to find a mechanism to cancel the aliasing error in the DFT polyphase filter bank. In 1993, Fliege proposed an approach to cancel the aliasing error [1–3]. He called the modified filter bank as modified DFT filter bank (MDFT). The first application of the MDFT filter bank in low-rate speech coding is found in [5], where the MDFT filter bank is used in a 16 kbit/s speech coder and the simulation showed a good code performance.
The MDFT filter bank proposed by Fliege belongs to time-invariant QMF filter banks. The channel number and subband filters do not change with time. In speech, audio and image processing, the time-varying filter bank can be used to adjust the input signal properties in order to get better processing performance [6, 7, 9, 10]. In the past, we have done a systematic research for the general time-varying filter bank including time-varying cosine-modulated filter banks [13–15]. In this paper, we want to use the established time-varying filter bank theory to analyze the time-varying MDFT filter bank (TV-MDFT), and investigate the properties of the MDFT filter bank in the case that its filter coefficients change with time. We want to also study the prototype filter design for a linear time-varying MDFT filter bank. After instruction Section 2 provides the description of the MDFT filter bank and its mechanism of aliasing error cancellation in both the time and frequency domain. Section 3 analyzes the time-varying MDFT filter bank including its PR condition and the relationship with time-varying cosine-modulated filter bank. In Section 4, the design of the prototype window filter for TV-MDFT is discussed. The well-know window switching method used in time-varying cosine-modulated filter bank [13] will be used in the prototype window design for TV-MDFT. Section 5 summarizes the main results of the paper.
2. MDFT Filter Bank
In [1], the mechanism of the alias cancellation in MDFT filter banks is just described in the frequency domain. Furthermore, the description in [1] seems not to be easy to understand. Here, we try to provide a clear mathematical description of the principle for an MDFT filter bank in both frequency and time domain.
2.1. In the Frequency Domain
Figure 1 shows an  -channel MDFT filter bank, where
-channel MDFT filter bank, where  is even. In the MDFT filter bank, the subband filters in both analysis and synthesis sides are derived from a linear phase FIR prototype filter
is even. In the MDFT filter bank, the subband filters in both analysis and synthesis sides are derived from a linear phase FIR prototype filter  by complex modulation. In the analysis side,
by complex modulation. In the analysis side,

The corresponding impulse response reads as

where  and
and  is called prototype window function or prototype filter.
is called prototype window function or prototype filter.
In the synthesis side, the synthesis subband filters are defined similarly as

The impulse response of the synthesis filters is given by

In order to cancel the aliasing errors in the filter band system showed in Figure 1 and achieve the perfect reconstruction, three key operations are introduced in the MDF filter banks [1].
Operation 1
Band limitation of the prototype filter  to
to  .
.
Operation 2
Separate each channel into two subchannels with two-step decimation plus interchanged real and imaginary operation.
Operation 3
Introduction of  sample delays in real or imaginary part in each subchannel interchangeably.
sample delays in real or imaginary part in each subchannel interchangeably.
Each of the three operations has its own contribution to alias cancellation in the MDF filter bank. The delay of the first subband will be done in the synthesis side, while the delay of the second subchannel in the analysis side. This is the key operation to cancel the adjacent aliasing spectrum.
The band limitation condition can be expressed as

The purpose of this condition is to limit the alias errors in the adjacent bands around the analysis subband. In the following, based on the defined condition and key operations we give the detailed analysis of the output-input relationship of an MDFT filter bank in the frequency domain and show how to use the above operations to cancel the alias components in the MDFT filter bank.
It is well known that the output signal  in an
in an  -channel maximally decimated time-invariant filter bank system can be formulated as
-channel maximally decimated time-invariant filter bank system can be formulated as

where  indicates the channel number. For an MDFT modulated filter bank, substituting (1) and (3) into (6), we get
indicates the channel number. For an MDFT modulated filter bank, substituting (1) and (3) into (6), we get

Using the band limitation condition, (7) can be further simplified as

From (8), we can see that the contribution of the  th channel to the output signal consists of three parts, the output through
th channel to the output signal consists of three parts, the output through  th channel
th channel  , the alias component in
, the alias component in  th channel
th channel  , and the alias component in the
, and the alias component in the  th channel
th channel  .
.
To cancel the alias components in the adjacent channels, the band limitation is not sufficient. We need still Operations 2 and 3. Operation 2 defines the two-step decimation, real and imaginary operation on the analysis filter output. The goal of the real and imaginary operation is to introduce the mirror spectra in the  th channel.Operation 3 introduces a sign factor
th channel.Operation 3 introduces a sign factor  in the first subchannel of each channel in order to move the alias component caused by the adjacent channels. In Figure 1, if we observe the signal
in the first subchannel of each channel in order to move the alias component caused by the adjacent channels. In Figure 1, if we observe the signal  in the synthesis side and take the
in the synthesis side and take the  delays in the synthesis side into account, we can write the real part of
delays in the synthesis side into account, we can write the real part of  as
as

Considering the fact that the signal  is got after
is got after  downsampling and upsampling, so, just the values of
downsampling and upsampling, so, just the values of  at
at  are not equal to zero and the other values of
are not equal to zero and the other values of  are zero, which means that
are zero, which means that  . Therefore,
. Therefore,  can be expressed as
can be expressed as

In the transform domain, we have

Note that the sign factor  is introduced by
is introduced by  delays in the synthesis side. This sign factor is independent of real and imaginary operation. So, all first subchannels in Figure 1, no matter the real and imaginary parts, have the sign factor
delays in the synthesis side. This sign factor is independent of real and imaginary operation. So, all first subchannels in Figure 1, no matter the real and imaginary parts, have the sign factor  .
.
The imaginary part of  is coming from the contribution of the second subchannel in the
is coming from the contribution of the second subchannel in the  th channel. From Figure 1, we have the imaginary part of
th channel. From Figure 1, we have the imaginary part of 

where  is the imaginary unit. Different from the first subchannel, in the second subchannel of the
is the imaginary unit. Different from the first subchannel, in the second subchannel of the  th channel, the
th channel, the  delays appear in the output of analysis filters. So, after downsampling and upsampling we get the no-zero values in the second subchannel just at
delays appear in the output of analysis filters. So, after downsampling and upsampling we get the no-zero values in the second subchannel just at  , which means that
, which means that  . Considering the
. Considering the  delay effects, we get
delay effects, we get

In the transform domain, we have

where there is no sign factor. In general, the second subchannel in Figure 1 has no sign factor.
To declare the mechanism of the adjacent spectrum cancellation in an MDFT filter bank, similar to [1], we suppose that the input spectrum  lies between the center frequency of the
lies between the center frequency of the  th and
th and  th channel showed in Figure 2. Note that the position of the input spectrum has no influence on the results.
th channel showed in Figure 2. Note that the position of the input spectrum has no influence on the results.
In Figure 2, the component  describes the mirror spectrum (M) with respect to the original spectrum (O)
describes the mirror spectrum (M) with respect to the original spectrum (O)  about the center frequency of the
about the center frequency of the  th channel because
th channel because  can be written as
can be written as  , while
, while  is equal to
is equal to  . AO denotes the alias component due to the shift version of the original spectrum in the
. AO denotes the alias component due to the shift version of the original spectrum in the  th channel. AM denotes the alias component caused by the shift version of the mirror spectrum in the
th channel. AM denotes the alias component caused by the shift version of the mirror spectrum in the  th channel.
th channel.
In the following description, we suppose that  is an even number. The result is suitable also for the case of odd
is an even number. The result is suitable also for the case of odd  . If the
. If the  is even, using (11) we get the real part of the
is even, using (11) we get the real part of the  th channel output in Figure 1 as
th channel output in Figure 1 as

where  is the alias component from the
is the alias component from the  th channel (AO), while
th channel (AO), while  is the alias component in the
is the alias component in the  th channel (AM). Both parts are coming from the real subchannels in
th channel (AM). Both parts are coming from the real subchannels in  th and
th and  th channels. From Figure 1, we know that the real subchannel in both
th channels. From Figure 1, we know that the real subchannel in both  th and
th and  th channels belongs to second subchannel which has no channel number dependent sign factor because the
th channels belongs to second subchannel which has no channel number dependent sign factor because the  delays are done in the analysis filters. So, the sign of the AO and AM components in (15) is positive. Similarly, the imaginary part of
delays are done in the analysis filters. So, the sign of the AO and AM components in (15) is positive. Similarly, the imaginary part of  has three contributions from imaginary subchannels in
has three contributions from imaginary subchannels in  th,
th,  th and
th and  th channels. Based on (14), we have
th channels. Based on (14), we have

where

are the alias components coming from the imaginary subchannels in  th and
th and  th subchannels, respectively. The sign factor is introduced because both imaginary subchannels belong to the second subchannel where the
th subchannels, respectively. The sign factor is introduced because both imaginary subchannels belong to the second subchannel where the  delays happen in the synthesis side. Up to now, we can better understand why the real and imaginary subchannels must be interchanged. This is exactly the requirement from alias cancellation.
delays happen in the synthesis side. Up to now, we can better understand why the real and imaginary subchannels must be interchanged. This is exactly the requirement from alias cancellation.
For the even  , adding (15) and (16) we get
, adding (15) and (16) we get

In (18), there is still one alias component needed to be canceled, that is, the alias of the mirror spectrum  lying in the
lying in the  th channel. Using the similar derivation for
th channel. Using the similar derivation for  , we get the output in the
, we get the output in the  th channel for the input
th channel for the input  and the mirror spectrum in
and the mirror spectrum in  th channel
th channel  as
as

where the mirror alias component has minus sign because the sign factor in(16) is positive after replacing  with
with  in (16), that is,
in (16), that is,  . Adding (18), and (19) we get the reconstruction output
. Adding (18), and (19) we get the reconstruction output

Defining

equation (20) can be written as

In the frequency domain, we get

A perfect MDFT filter bank requires that  must be constant and
must be constant and  should be linear function of variable
should be linear function of variable  . If the prototype filter
. If the prototype filter  has linear phase, we have possibility to satisfy the requirement. Based on [16], a linear phase FIR filter can be described as
has linear phase, we have possibility to satisfy the requirement. Based on [16], a linear phase FIR filter can be described as

where  is the filter length,
is the filter length,  is real function for
is real function for  . Using (24), we can write
. Using (24), we can write  as
as

If

which means that if the frequency response of the prototype filter is power complementary, we can get the reconstructed signal without distortion. From [16], we know that a linear phase FIR filter can only have two non-zero filter coefficients if the power complementary condition given in (23) must be at the same time satisfied. Such a linear phase FIR filter has worse frequency characteristics and is not useful. Another prototype window is introduced in [1], which is derived from an ideal transform function consisting of a square root raised-cosine function and satisfying the power complementary condition (23). But such a prototype window is infinite and noncausal. To make it useful, the truncation and time shift must be done on the prototype window. The finite prototype window is no more power complementary. So, in practice, the condition (23) needs to be given up by designing the prototype filter for an MDFT filter bank. However, it is possible to keep the amplitude distortion arbitrarily small by designing the prototype filter [2].
2.2. In the Time Domain
To make the analysis in the time domain possible, we need to use another structure of the MDFT filter bank, namely, structure with two filter banks without real and imaginary operation shown in Figure 3.
The filter bank in Figure 3 is a 2 -channel oversampling filter bank with factor 2. The analysis filter in
-channel oversampling filter bank with factor 2. The analysis filter in  can be described as
can be described as

where  is the imaginary unit. The analysis filters in the
is the imaginary unit. The analysis filters in the  have the form
have the form

The synthesis filter is defined by


where  . Suppose that the analysis and synthesis filters have length
. Suppose that the analysis and synthesis filters have length  . In order to describe the MDFT filter bank in the time domain, we need to define the following
. In order to describe the MDFT filter bank in the time domain, we need to define the following  matrices:
matrices:



where  ,
,  , and
, and  .
.
For analysis of the MDFT filter bank in the time domain, we define two infinite matrices  and
and  as
as


 and
and  are called analysis and synthesis matrices and describe the relationship of the MDFT analysis and synthesis filter bank coefficients during the filter bank operation in the time domain. These two infinite matrices are the basis for the analysis of MDFT filter bank in the time domain. Using the matrices (31)-(33) and (34)-(35), we can describe the MDFT filter bank operation in the time domain as
are called analysis and synthesis matrices and describe the relationship of the MDFT analysis and synthesis filter bank coefficients during the filter bank operation in the time domain. These two infinite matrices are the basis for the analysis of MDFT filter bank in the time domain. Using the matrices (31)-(33) and (34)-(35), we can describe the MDFT filter bank operation in the time domain as

where  and
and  are the input and output vectors defined, respectively, by
are the input and output vectors defined, respectively, by

It is clear that the perfect reconstruction (PR) condition for the MDFT filter bank is

where  is an infinite unit matrix. Together with (26), we have the following theorem.
is an infinite unit matrix. Together with (26), we have the following theorem.
Theorem 1.
The following PR conditions are equivalent for an MDFT filter bank
-
(1)
 ,
,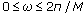 ,
, -
(2)
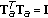 .
.
2.3. Relationship with Cosine-Modulated Filter Bank
If we remove the imaginary channels in Figure 1, the channel number in  and
and  reduces to
reduces to  . Then, an MDFT filter bank becomes a critically decimated
. Then, an MDFT filter bank becomes a critically decimated  -channel filter bank with real filter coefficients. The filter definitions in (27) and (28) can be simplified as
-channel filter bank with real filter coefficients. The filter definitions in (27) and (28) can be simplified as

where  . After removing the imaginary channels in the MDFT filter bank, the mechanism described above for alias cancellation does not work, because the sign factor introduced by
. After removing the imaginary channels in the MDFT filter bank, the mechanism described above for alias cancellation does not work, because the sign factor introduced by  delays has no contribution to alias cancellation. So, the two stages sampling and
delays has no contribution to alias cancellation. So, the two stages sampling and  delays make no sense. Removing the delay
delays make no sense. Removing the delay  in Figure 3, we get an
in Figure 3, we get an  -channel cosine-modulated filter bank in Figure 4.
-channel cosine-modulated filter bank in Figure 4.
The filters in Figure 4 are defined as

From [11, 13], we know that it is possible to get a perfectly reconstructed cosine-modulated filter bank if the phase  is properly selected. It is clear that the phase
is properly selected. It is clear that the phase  does not get perfect reconstruction. One possible
does not get perfect reconstruction. One possible  that leads to a perfectly reconstructed cosine-modulated filter bank is [13]
that leads to a perfectly reconstructed cosine-modulated filter bank is [13]

3. Design of MDFT Filter Bank
The design of the MDFT filter bank is based on Theorem 1. Using the PR condition (2) in Theorem 1, the design can be formulated as the following equation

where e is the error vector. The design is an optimization process to find the filter coefficients in  at the minimal error point. This optimization needs a large computation efforts. So, it is not the first choice for the MDFT filter bank design.
at the minimal error point. This optimization needs a large computation efforts. So, it is not the first choice for the MDFT filter bank design.
Another method is to use the PR condition (1) in Theorem 1. Here we can use the design approach of the FIR filter, where the filter coefficients of an ideal low-pass filter are first got through inverse transform. Then, the FIR filter coefficients are attained by windowing the infinite idea low pass filter coefficients. A possible ideal prototype filter satisfying the power complementary is the square root raised-cosine function defined by [2]

where  is the cut-off frequency. For an MDFT filter bank,
is the cut-off frequency. For an MDFT filter bank,  is equal to
is equal to  .
.  is the roll-off factor
is the roll-off factor  and decides the weight of transient band of the filter.
and decides the weight of transient band of the filter.  is ideal for an MDFT filterbank because
is ideal for an MDFT filterbank because

Through inverse transform of  we have the impulse response function of the prototype filter as [2]
we have the impulse response function of the prototype filter as [2]

An MDFT filter bank with  has perfect reconstruction. But
has perfect reconstruction. But  is infinite and noncausal. So,
is infinite and noncausal. So,  is unrealisable. To get the realisable and causal prototype filter, we can simply truncate and shift the function
is unrealisable. To get the realisable and causal prototype filter, we can simply truncate and shift the function  . After truncating and time shifting, we have
. After truncating and time shifting, we have

where  is the prototype filter length. From [2], we know that it is possible to keep the aliasing distortion arbitrarily small by selecting the roll-off factor
is the prototype filter length. From [2], we know that it is possible to keep the aliasing distortion arbitrarily small by selecting the roll-off factor  and the window function
and the window function  . Figure 5 shows the examples of the transfer function
. Figure 5 shows the examples of the transfer function  and its corresponding truncating impulse response function
and its corresponding truncating impulse response function  with roll-off factor
with roll-off factor  and
and  , respectively.
, respectively.
4. Time-Varying MDFT Filter Bank
The general time-varying filter bank is studied in [14, 15]. In [13], the time-varying cosine-modulated filter bank is analyzed. The window switching methods are introduced to design the time-varying cosine-modulated filter bank. The MDFT filter bank is same as the cosine-modulated filter bank in that both filter banks are got through modulation of a prototype filter. The difference is that cosine-modulated filter banks use a cosine function as the modulation function while the modulator in the MDFT filter bank is complex valued. So, the window switching methods can also be used in design of MDFT filter banks. In the following, we give firstly the description of a time-varying MDFT filter bank with focus on an  -channel time-varying filter bank. Then, the window switching methods are used to design the
-channel time-varying filter bank. Then, the window switching methods are used to design the  -channel time-varying filter bank.
-channel time-varying filter bank.
4.1. Description of Time-Varying MDFT Filter Bank
Similar to that in [15], we define an  -channel time-varying MDFT filter bank as the MDFT filter bank whose analysis and synthesis filter coefficients are varying with the index
-channel time-varying MDFT filter bank as the MDFT filter bank whose analysis and synthesis filter coefficients are varying with the index  , where
, where  is the integer part of
is the integer part of  . Figure 6 shows an
. Figure 6 shows an  -channel time-varying MDFT filter bank.
-channel time-varying MDFT filter bank.
The filter coefficients in (27)-(28) become


where  is the time-varying prototype filter.
is the time-varying prototype filter.  is defined as
is defined as

 and
and  have the similar definitions. The time-varying analysis matrix
have the similar definitions. The time-varying analysis matrix  has the form
has the form

Similarly, replacing  and
and  with
with  and
and  in (35) we have the time-varying synthesis matrix
in (35) we have the time-varying synthesis matrix 

The PR condition of the time-varying MDFT filter bank is

The power complementary condition at each time index  does not make sure that the time-varying MDFT filter bank has a PR property. We know that the convolution rule in a time-invariant system does not exist in a time-varying system [14]. So, the frequency-domain analysis method for the aliasing cancellation described in Section 2 cannot be used for analyzing the time-varying MDFT filter banks. The time-domain analysis method is more efficient for the time-varying filter bank analysis and design.
does not make sure that the time-varying MDFT filter bank has a PR property. We know that the convolution rule in a time-invariant system does not exist in a time-varying system [14]. So, the frequency-domain analysis method for the aliasing cancellation described in Section 2 cannot be used for analyzing the time-varying MDFT filter banks. The time-domain analysis method is more efficient for the time-varying filter bank analysis and design.
4.2. Design of Time-Varying MDFT Filter Banks
The basis of filter bank design is its PR condition. In the time-invariant case, we can use the power complementary condition (38) to design the time-invariant MDFT filter bank. But, the power complementary condition does not exist for the time-varying MDFT filter bank. So, the only useful design condition is the PR condition (52). The general design approach for a time-varying filter bank is introduced in [17]. In [17], the least squares (LS) solution is provided to calculate the synthesis filter coefficients in the transient period from one MDFT filter bank to another MDFT filter bank. But, the LS solution needs the calculation of the inverse matrix. In [13], a window switching method is introduced to design the time-varying cosine-modulated filter bank, where the prototype filter impulse response function or the prototype window function in the transient period is got through changing the pieces of window based on the prototype windows before and after changing at the time  . The window switching method does not need any calculation. It is quite useful for the design of time-varying filter bank with modulation of the prototype filter because in such a filter bank system the filter coefficients are described by prototype filter. We just need to design the prototype window function at each time index
. The window switching method does not need any calculation. It is quite useful for the design of time-varying filter bank with modulation of the prototype filter because in such a filter bank system the filter coefficients are described by prototype filter. We just need to design the prototype window function at each time index  . In the following, we give an example to describe how to design the time-varying MDFT filter bank using window switching methods.
. In the following, we give an example to describe how to design the time-varying MDFT filter bank using window switching methods.
Before using window switching methods to design the prototype filter, we need to know the restrictions that the PR condition imposes on the prototype filter  . We define following matrices:
. We define following matrices:

where





where  ,
,  , and
, and  .
.
Using matrices (54)–(58), we can write the analysis matrix in (48) as

Similarly, we have



According to the PR condition in (52), we get the following equations:


where  ,
,  . I is the
. I is the  unit matrix. Substituting (61)-(62) into (63)-(64), we have
unit matrix. Substituting (61)-(62) into (63)-(64), we have

To simplify the above equations, we need to select  (
( ), so that
), so that

It is clear that the definitions in (54)–(57) do not satisfy the condition (66). Therefore, a time-varying MDFT filter bank that has the prototype filter with limited length cannot be perfectly reconstructed. However, it is possible to get the small distortion using the window switching methods, which can be achieved through keeping the prototype window as soon as possible by switching the windows in the transient periods.
In the following we give an example to describe how to design the time-varying MDFT filter bank using window switching methods. Suppose that at time  we want to switch from an MDFT filter bank with roll-off factor
we want to switch from an MDFT filter bank with roll-off factor  to another MDFT filter bank with roll-off factor
to another MDFT filter bank with roll-off factor  . The prototype windows are showed in Figures 5(c) and 5(d), respectively. We first represent the analysis matrix
. The prototype windows are showed in Figures 5(c) and 5(d), respectively. We first represent the analysis matrix  around
around  using block diagram schematically in Figure 7.
using block diagram schematically in Figure 7.
From Figure 7, we can see that the reconstructed signal at each time point in this example is related to two analysis filter banks after this time point, which means that the filter bank change at time point  has impact on the reconstructed signals at time point
has impact on the reconstructed signals at time point  and
and  . Since time point
. Since time point  the MDFT filter bank uses the new filter bank. The filter bank at time point
the MDFT filter bank uses the new filter bank. The filter bank at time point  is the bridge from the old filter bank to the new filter bank. So, we need to decide the prototype filters at
is the bridge from the old filter bank to the new filter bank. So, we need to decide the prototype filters at  in order to keep the small distortions due to the filter bank switching. According to the principle that the prototype filters in the transient period should contain the prototype filters before and after switching, we can simply keep the window pieces in the second part of the prototype window at time point
in order to keep the small distortions due to the filter bank switching. According to the principle that the prototype filters in the transient period should contain the prototype filters before and after switching, we can simply keep the window pieces in the second part of the prototype window at time point  and replace the window pieces in the first part. Using this method we get the window matrices around
and replace the window pieces in the first part. Using this method we get the window matrices around  , where the window matrix is attained through replacing the blocks in Figure 7 with the corresponding prototype windows (see Figure 8).
, where the window matrix is attained through replacing the blocks in Figure 7 with the corresponding prototype windows (see Figure 8).
Window matrix for Figure 7.
To show the advantage of the introduced prototype window design method in comparison with the direct switching, we define two matrices around the time index  for the above example based on the
for the above example based on the  and
and  definitions in (50), (51), and the graphical representation in Figure 7 as
definitions in (50), (51), and the graphical representation in Figure 7 as


Suppose that the MDFT filter banks before and after the time point  have very small alias errors which can be considered as zero. Multiplying matrices in (67) and (68), we get alias matrix
have very small alias errors which can be considered as zero. Multiplying matrices in (67) and (68), we get alias matrix

where  and
and  (
( represent the alias errors introduced by the transition period from
represent the alias errors introduced by the transition period from  to
to  . For a perfectly reconstructed time-varying MDFT filter bank and
. For a perfectly reconstructed time-varying MDFT filter bank and  , where
, where  is the
is the  unit matrix. The other alias matrices should be zero. To show that the alias errors using window switching methods are smaller than that alias errors in the direct switch, we rewrite the matrices
unit matrix. The other alias matrices should be zero. To show that the alias errors using window switching methods are smaller than that alias errors in the direct switch, we rewrite the matrices  and
and  based on the window switching methods as
based on the window switching methods as


The corresponding alias error matrix reads

To measure the alias error, we define the average signal-to-noise rate (AVSNR) as

where  and
and  are the row vectors in
are the row vectors in  and
and  , respectively.
, respectively.  is the row vector of the following matrix
is the row vector of the following matrix

Simulation results show that

So, we say that the window switching design method can reduce the alias errors in the transition period than the direct switch.
The simulation is done in Matlab. The prototype filter coefficients are calculated according to (45) with roll-off factor  and
and  , respectively. The filter bank coefficients are attained using (27)–(30). The MDFT filter banks before time
, respectively. The filter bank coefficients are attained using (27)–(30). The MDFT filter banks before time  have prototype filter with roll-off factor 0.3. After time
have prototype filter with roll-off factor 0.3. After time  , the prototype filter of the MDFT filter banks has the roll-off factor
, the prototype filter of the MDFT filter banks has the roll-off factor  .
.
Here, we have some remarks on the structure in matrices (70) and (71). The matrix  is the synthesis matrix, and the matrix
is the synthesis matrix, and the matrix  is the analysis matrix. In
is the analysis matrix. In  all coefficients are coming from the MDFT filter bank at time
all coefficients are coming from the MDFT filter bank at time  , which means that the synthesis filter bank does not need to be redesigned during the transition period. We need just to redesign the analysis filter banks. This can reduce the design complexity. Based on the principle of window switching methods, at time
, which means that the synthesis filter bank does not need to be redesigned during the transition period. We need just to redesign the analysis filter banks. This can reduce the design complexity. Based on the principle of window switching methods, at time  the prototype window pieces in the first half part should be replaced by the prototype window in the second half part at time
the prototype window pieces in the first half part should be replaced by the prototype window in the second half part at time  . But this principle is a general principle. In the concrete application, we should make some adjustments. From Figure 3 we know that an MDFT filter bank consists of two filter banks with
. But this principle is a general principle. In the concrete application, we should make some adjustments. From Figure 3 we know that an MDFT filter bank consists of two filter banks with  sample delays of each other. The prototype window in the window matrix in Figure 7 has also
sample delays of each other. The prototype window in the window matrix in Figure 7 has also  sample delays, which leads to that one piece of prototype window at time
sample delays, which leads to that one piece of prototype window at time  is involved in the filter bank operation at time
is involved in the filter bank operation at time  . So, we need to replace
. So, we need to replace  in (71) with
in (71) with  to make the matrix element
to make the matrix element  in (72) equal to I. Similarly, we need to replace
in (72) equal to I. Similarly, we need to replace  in (71) with
in (71) with  to make sure that the alias error
to make sure that the alias error  .
.
5. Conclusion
In this paper, we have analyzed the time-varying MDFT filter bank in detail in both frequency and time domain. The mechanism of the aliasing cancellation for the time-invariant MDFT is presented. The PR conditions for the time-varying and time-invariant MDFT filter banks are given. For the design of time-varying MDFT filter banks, we used the window switching methods. The example shows that the window switching method is simple and useful, in particular for the design of time-varying filter banks with modulation, such as time-modulated cosine filter bank and time-varying MDFT filter bank.
References
Fliege NT: Modified DFT polyphase SBC filter banks with almost perfect recomstruction. Proceeding of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '94), April 1994
Fliege NJ: Closed form design of prototype filters for linear phase DFT polyphase filter banks. Proceedings of IEEE International Symposium on Circuits and Systems, May 1994 651-654.
Fliege NJ: Computational efficiency of modified DFT polyphase filter banks. Proceedings of the 27th Asilomar Conference on Signals, Systems & Computers, November 1993 1296-1300.
Karp T, Fliege NJ: Modified DFT filter banks with perfect reconstruction. IEEE Transactions on Circuits and Systems II 1999, 46(11):1404-1414. 10.1109/82.803480
Wang G: Analysis of quantization errors in subband speech coding with modified DFT filter banks. Signal Processing 2006, 86(2):341-352. 10.1016/j.sigpro.2005.05.018
ISO/IEC JTCI/SC29 : Information technology-coding of moving pictures and associated audio for digital storage media at up to about 1.5 Mbit/s-IS 11172-3 (audio). 1992
Shlien S: The modulated lapped transform, its time-varying forms, and its applications to audio coding standards. IEEE Transactions on Speech and Audio Processing 1997, 5(4):359-366. 10.1109/89.593311
Bellangerr MG, Daguet JL: TDM-FDM Transmultiplexer: Digital Polyphase and FFT. IEEE Transactions on Comunnication 1974, 22: 1199-1294. 10.1109/TCOM.1974.1092391
Yue R, Vorobyov SA, Gershman AB: Adaptive OFDM techniques with one-bit-per-subcarrier channel-state feedback. IEEE Transactions on Communications 2006, 54(11):1993-2003.
Sandeep Pradhan S, Reddy VU: A new approach to subband adaptive filtering. IEEE Transactions on Signal Processing 1999, 47(3):655-664. 10.1109/78.747773
Vaidyanathan PP: Multirate digital filters, filter banks, polyphase networks, and applications: a tutorial. Proceedings of the IEEE 1990, 78(1):56-93. 10.1109/5.52200
Malvar HS: Signal Processing with Lapped Transforms. Artech House, Boston, Mass, USA; 1992.
Wang G: Time-varying cosine-modulated filter banks. Digital Signal Processing 2005, 15(3):237-254. 10.1016/j.dsp.2004.09.007
Wang G: The most general time-varying filter bank and time-varying lapped transforms. IEEE Transactions on Signal Processing 2006, 54(10):3775-3789.
Wang G: Analysis of M-channel time-varying filter banks. Digital Signal Processing 2008, 18(2):127-147. 10.1016/j.dsp.2007.02.006
Heute U: Noise reduction. In Topics in Acoustic Echo and Noise Control. Edited by: Haensler E, Schmidt G. Springer, Berlin, Germany; 2006:325-384.
Vaidyanathan PP: Multirate Systems and Filter Banks, Signal Processing Series. Prentice-Hall, Englewood Cliffs, NJ, USA; 1993.
Wang G: Time-varying discrete-time signal expansions as time-varying filter banks. IET Signal Processing 2009, 3(5):353-367. 10.1049/iet-spr.2008.0049
Acknowledgment
This work is supported by the National Natural Science Foundation of China (no. 61071195).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, G., Zhang, Z. & Chen, Q. Analysis and Properties of Time-Varying Modified DFT Filter Banks. EURASIP J. Adv. Signal Process. 2010, 342865 (2010). https://doi.org/10.1155/2010/342865
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/342865



 ,
,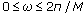 ,
,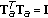 .
.

 and its deduced prototype filter coefficients h(n) at different roll-off factor r. (a)
and its deduced prototype filter coefficients h(n) at different roll-off factor r. (a)  with r = 0.3 (b)
with r = 0.3 (b)  with r = 0.5 (c) h(n) with N = 2M, r = 0.3, w(n) = 1 (d) h(n) with N = 2M, r = 0.5, w(n) = 1
with r = 0.5 (c) h(n) with N = 2M, r = 0.3, w(n) = 1 (d) h(n) with N = 2M, r = 0.5, w(n) = 1

 around time point m.
around time point m.