- Research Article
- Open access
- Published:
Parametric Adaptive Radar Detector with Enhanced Mismatched Signals Rejection Capabilities
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 375136 (2010)
Abstract
We consider the problem of adaptive signal detection in the presence of Gaussian noise with unknown covariance matrix. We propose a parametric radar detector by introducing a design parameter to trade off the target sensitivity with sidelobes energy rejection. The resulting detector merges the statistics of Kelly's GLRT and of the Rao test and so covers Kelly's GLRT and the Rao test as special cases. Both invariance properties and constant false alarm rate (CFAR) behavior for this detector are studied. At the analysis stage, the performance of the new receiver is assessed and compared with several traditional adaptive detectors. The results highlight better rejection capabilities of this proposed detector for mismatched signals. Further, we develop two two-stage detectors, one of which consists of an adaptive matched filter (AMF) followed by the aforementioned detector, and the other is obtained by cascading a GLRT-based Subspace Detector (SD) and the proposed adaptive detector. We show that the former two-stage detector outperforms traditional two-stage detectors in terms of selectivity, and the latter yields more robustness.
1. Introduction
Adaptive detection of signals embedded in Gaussian or non-Gaussian disturbance with unknown covariance matrix has been an active research field in the last few decades. Several generalized likelihood ratio test- (GLRT-) based methods are proposed, which utilize secondary (training) data, that is, data vectors sharing the same spectral properties, to form an estimate of the disturbance covariance. In particular, Kelly [1] derives a constant false alarm rate (CFAR) test for detecting target signals known up to a scaling factor; Robey et al. [2] develops a two-step GLRT design procedure, called adaptive matched filter (AMF). Based on the above methods, some improved approaches have been proposed, for example, the non-Gaussian version of Robey's adaptive strategy in [3–6] and the extended targets version of Kelly's adaptive detection strategy in [7]. In addition, considering the presence of mutual coupling and near-field effects, De Maio et al. [8] redevises Kelly's GLRT detector and the AMF.
Most of the above methods work well, provided that the exact knowledge of the signal array response vector is available; however, they may experience a performance degradation in practice when the actual steering vector is not aligned with the nominal one. A side lobe mismatched signal may appear subject to several causes, such as calibration and pointing errors, imperfect antenna shape, and wavefront distortions. To handle such mismatched signals, the Adaptive Beamformer Orthogonal Rejection Test (ABORT) [9] is proposed, which takes the rejection capabilities into account at the design stage, introducing a tradeoff between the detection performance for main lobe signals and rejection capabilities for side lobe ones. The directivity of this detector is in between that of the Kelly's GLRT and the Adaptive Coherence Estimator (ACE) [10, 11]. A Whitened ABORT (W-ABORT) [12, 13] is proposed to address adaptive detection of distributed targets embedded in homogeneous disturbance via GLRT and the useful and fictitious signals orthogonal in the whitened space, which has an enhanced rejection capability for side lobe signals. Some alternative approaches are devised [14–17], which basically depend on constraining the actual signature to span a cone, whose axis coincides with its nominal value. Moreover, in [18], a detector based on the Rao test criterion is introduced and assessed. It is worth noting that the Rao test exhibits discrimination capabilities of mismatched signals better than those of the ABORT, although it does not consider a possible spatial signature mismatch at the design stage.
From another point of view, increased robustness to mismatch signals can be obtained by two-stage tunable receivers that are formed by cascading two detectors (usually with opposite behaviors), in which case, only data vectors exceeding both detection thresholds will be declared as the target bearings [19–23]. Remarkably, such solutions can adjust directivity by proper selection of the two thresholds to trade good rejection capabilities of side lobe signals for an acceptable detection loss for matched signals. An alternative approach to design tunable receivers relies on the parametric adaptive detectors, which allow us to trade off target sensitivity with side lobes energy rejection via tuning a design parameter [24, 25]. In particular, in [24], Kalson devises a parametric detector obtained by merging the statistics of Kelly's GLRT and of the AMF, whereas in [25], Bandiera et al. propose another parametric adaptive detector, which is obtained by mixing the statistic of Kelly's GLRT with that of the W-ABORT.
In this paper, we attempt to increase the rejection capabilities of tunable receivers and develop a novel adaptive parametric detector, which is obtained by merging the statistics of the Kelly's GLRT and of the Rao test. We show that the proposed detector is invariant under the group of transformations defined in [26]. As a consequence, it ensures the CFAR property with respect to the unknown covariance matrix of the noise. The performance assessment, conducted analytically for matched and mismatched signals, highlights that specified with a appropriate design parameter the new detector has better rejection capabilities for side lobe targets than existing decision schemes. However, if the value of the design parameter is bigger than or equals to unity, this new detector leads to worse detection performance than Kelly's receiver. To circumvent this drawback, a two-stage detector is proposed, which consists of the AMF followed by the proposed parametric adaptive detector and can be taken as an improved alternative of the two-stage detector in [18]. We also give another two-stage detector with enhanced robustness, which is obtained by cascading the GLRT-based Subspace Detector (SD) [27] and the proposed parametric adaptive receiver.
The paper is organized as follows. In the next section, we formulate the problem and then propose the adaptive parametric detector. In Section 3, we analyze the performance of the proposed receiver. We present two newly proposed two-stage tunable detectors, respectively, in Sections 4 and 5. Section 6 contains conclusions and avenues for further research. Finally, some analytical derivations are given in the Appendix.
2. Problem Formulation and Design Issues
We assume that data are collected from  sensors and denote by
sensors and denote by  the complex vector of the samples where the presence of the useful signal is sought (primary data). As customary, we also suppose that a secondary data set
the complex vector of the samples where the presence of the useful signal is sought (primary data). As customary, we also suppose that a secondary data set  ,
,  , is available (
, is available ( ), that each of such snapshots does not contain any useful target echo and exhibits the same covariance matrix as the primary data (homogeneous environment).
), that each of such snapshots does not contain any useful target echo and exhibits the same covariance matrix as the primary data (homogeneous environment).
The detection problem at hand can be formulated in terms of the following binary hypothesis test:

where
-
(i)
 and
and 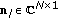 ,
,  , are independent, complex, zero-mean Gaussian vectors with covariance matrix given by
, are independent, complex, zero-mean Gaussian vectors with covariance matrix given by (2)
(2)where
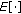 denotes expectation and
denotes expectation and 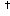 conjugate transposition;
conjugate transposition; -
(ii)
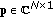 is the unit-norm steering vector of main lobe target echo, which is possibly different from that of the nominal steering vector
is the unit-norm steering vector of main lobe target echo, which is possibly different from that of the nominal steering vector 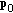 ;
; -
(iii)
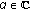 is an unknown deterministic factor which accounts for both target reflectivity and channel effects.
is an unknown deterministic factor which accounts for both target reflectivity and channel effects.
The Rao test for the above problem [18] is given by

where  is
is  times the sample covariance matrix of the secondary data, that is,
times the sample covariance matrix of the secondary data, that is,  . It is straightforward to show that
. It is straightforward to show that  can be recast as
can be recast as

where

is the AMF decision statistic, and

is the decision statistic of Kelly's GLRT.
Comparing  with
with  , we propose a new detector, termed KRAO in the following. Its decision statistic is
, we propose a new detector, termed KRAO in the following. Its decision statistic is

or, equivalently

where  is the design parameter.
is the design parameter.
It is clear that our detector covers Kelly's GLRT and the Rao test as special cases, respectively, when  and
and  . Moreover, since
. Moreover, since  can be expressed in terms of the maximal invariant statistic (
can be expressed in terms of the maximal invariant statistic ( ,
,  ), it is invariant with respect to the transformations defined in [26]. As a consequence, it ensures the CFAR property with respect to the unknown covariance matrix of the noise.
), it is invariant with respect to the transformations defined in [26]. As a consequence, it ensures the CFAR property with respect to the unknown covariance matrix of the noise.
3. Performance Assessment
In this section, we derive an analytic expression of  and
and  and then present illustrative examples for KRAO. Specifically, in derivation of
and then present illustrative examples for KRAO. Specifically, in derivation of  , we consider a general case, in which the signal in the primary data vector is not commensurate with the nominal steering vector, that is we consider detection performance for mismatched signal. To this end, we first introduce the random variable
, we consider a general case, in which the signal in the primary data vector is not commensurate with the nominal steering vector, that is we consider detection performance for mismatched signal. To this end, we first introduce the random variable

and then consider the equivalent form of Kelly's statistic  . Thus,
. Thus,  can be expressed to be
can be expressed to be

3.1. 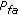 of the KRAO
of the KRAO
Under  hypothesis, the following statements hold [21]:
hypothesis, the following statements hold [21]:
-
(i)
given
 ,
,  is ruled by the complex central F-distribution with 1,
is ruled by the complex central F-distribution with 1, 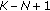 degrees of freedom, namely,
degrees of freedom, namely,  ;
; -
(ii)
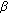 is a complex central beta distribution random variable (rv) with
is a complex central beta distribution random variable (rv) with 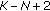 ,
, 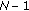 degrees of freedom, namely,
degrees of freedom, namely, 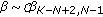 .
.
Therefore, the KRAO associated  satisfies
satisfies

where  is the threshold set beforehand, whose value depends on the value of
is the threshold set beforehand, whose value depends on the value of  ,
,  is the probability density function (pdf) of the rv
is the probability density function (pdf) of the rv  , and
, and  is the cumulative distribution function (cdf) of the rv
is the cumulative distribution function (cdf) of the rv  , given
, given  . Then it follows
. Then it follows

Substituting (12) into (11) followed by some algebra, it yields
-
(i)
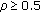 and
and 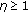
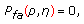 (13)
(13) -
(ii)
 and
and 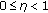
 (14)
(14) -
(iii)
 and
and 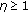
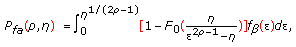 (15)
(15) -
(iv)
 and
and 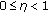
 (16)
(16)
For the reader ease, Figure 1 shows the contour plots for the KRAO corresponding to different values of  , as functions of the threshold pairs (
, as functions of the threshold pairs ( ,
,  ),
),  , and
, and  . All curves have been obtained by means of numerical integration techniques.
. All curves have been obtained by means of numerical integration techniques.
3.2. 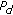 of the KRAO
of the KRAO
Now we consider hypothesis  . Denote
. Denote  the angle between
the angle between  and
and  in the whitened-dimensional data space, that is,
in the whitened-dimensional data space, that is,

The term  is a measure of the mismatch between
is a measure of the mismatch between  and
and  . Its value is one for the matched case where
. Its value is one for the matched case where  , and less than one otherwise. A small value of
, and less than one otherwise. A small value of  implies a large mismatch between the steering vector and signal. In this case, due to the useful signal components, distributions of
implies a large mismatch between the steering vector and signal. In this case, due to the useful signal components, distributions of  and
and  are given in [23]:
are given in [23]:
-
(i)
given
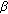 ,
,  is ruled by the complex noncentral F-distribution with 1,
is ruled by the complex noncentral F-distribution with 1,  degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter (18)
(18)namely,
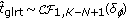 , where
, where 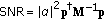 is the total available signal-to-noise ratio;
is the total available signal-to-noise ratio; -
(ii)
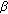 is a complex noncentral beita distribution rv with
is a complex noncentral beita distribution rv with 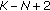 ,
,  degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter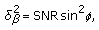 (19)
(19)namely,
 .
.
Then  is given by
is given by

where  is the pdf of the rv
is the pdf of the rv  , and then, given
, and then, given  ,
,  is the cdf of the rv
is the cdf of the rv  .
.
Similarly as before (in Section 3.1), we have
-
(i)
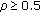 and
and 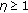
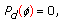 (21)
(21) -
(ii)
 and
and 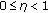
 (22)
(22) -
(iii)
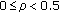 and
and 
 (23)
(23) -
(iv)
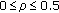 and
and 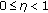
 (24)
(24)
In the case of a perfect match,  is equal to zero. As a consequence,
is equal to zero. As a consequence,  is distributed as a complex central beta distribution random variable with
is distributed as a complex central beta distribution random variable with  ,
,  degrees of freedom, and
degrees of freedom, and  is ruled by the complex noncentral F-distribution with 1,
is ruled by the complex noncentral F-distribution with 1,  degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter

3.3. Performance Analysis
In this subsection, we present numerical examples to illustrate the performance of the KRAO. The curves are obtained by numerical integration and the probability of false alarm is set to  .
.
One can see the influence of the design parameter  in Figures 2 and 3, where the
in Figures 2 and 3, where the  of the KRAO is plotted versus the SNR, considering both the case of a perfect match between the actual steering vector and the nominal one, namely,
of the KRAO is plotted versus the SNR, considering both the case of a perfect match between the actual steering vector and the nominal one, namely,  , and the case where there is a misalignment between the two aforementioned vectors, more precisely
, and the case where there is a misalignment between the two aforementioned vectors, more precisely  . Specifically, Figures 2 and 3 correspond to
. Specifically, Figures 2 and 3 correspond to  and
and  , respectively. From Figure 2, we see that the curves associated with the KRAO are in between that of Kelly's GLRT and that of the Rao test when
, respectively. From Figure 2, we see that the curves associated with the KRAO are in between that of Kelly's GLRT and that of the Rao test when  , and that the KRAO outperforms the Rao test in terms of selectivity for
, and that the KRAO outperforms the Rao test in terms of selectivity for  . However, it is also shown that the amount of detection loss for matched signals and sensitivity to mismatched signals depend upon the design parameter
. However, it is also shown that the amount of detection loss for matched signals and sensitivity to mismatched signals depend upon the design parameter  . More specifically, a larger value of
. More specifically, a larger value of  leads to better rejection capabilities of the side lobe signals and the larger detection loss for matched signals. On the other hand, Figure 3 shows that, when
leads to better rejection capabilities of the side lobe signals and the larger detection loss for matched signals. On the other hand, Figure 3 shows that, when  , a smaller value of
, a smaller value of  renders the performance less sensitive to mismatched signals. In another word, robustness to mismatched signals can be increased by setting
renders the performance less sensitive to mismatched signals. In another word, robustness to mismatched signals can be increased by setting  . In summary, different values of
. In summary, different values of  represent different compromises between the detection and the rejection performance. So the appropriate value of
represent different compromises between the detection and the rejection performance. So the appropriate value of  is selected based on the system needs.
is selected based on the system needs.
In Figures 4 and 5, we compare the KRAO to the ACE, the ABORT, and Bandiera's detector (KWA) [25] for  ,
,  , and under the constraint that the loss with respect to Kelly's GLRT is practically the same for the perfectly matched case. For sake of completeness, we review these CFAR detectors in the following:
, and under the constraint that the loss with respect to Kelly's GLRT is practically the same for the perfectly matched case. For sake of completeness, we review these CFAR detectors in the following:

where  is the design parameter of the KWA. From Figures 4 and 5, it is clear that the KRAO is superior to the KWA in rejecting side lobe signals with
is the design parameter of the KWA. From Figures 4 and 5, it is clear that the KRAO is superior to the KWA in rejecting side lobe signals with  It is also clear that, with a proper choice of
It is also clear that, with a proper choice of  , the KRAO outperforms the ACE and the ABORT in terms of selectivity. Other simulation results not reported here, in order not to burden too much the analysis, have shown that the above results are still valid for
, the KRAO outperforms the ACE and the ABORT in terms of selectivity. Other simulation results not reported here, in order not to burden too much the analysis, have shown that the above results are still valid for  and
and  .
.
4. Two-Stage Detector Based on the KRAO
In this section, we propose a two-stage algorithm, aiming at compensating the matched detection performance loss for the KRAO with  . Briefly, this is obtained by cascading the AMF and the KRAO (
. Briefly, this is obtained by cascading the AMF and the KRAO ( ). We term this two-stage detector KRAO Adaptive Side lobe Blanker (KRAO-ASB). This detector generalizes the two-stage Rao test (AMF-RAO) [18] for
). We term this two-stage detector KRAO Adaptive Side lobe Blanker (KRAO-ASB). This detector generalizes the two-stage Rao test (AMF-RAO) [18] for  . We now summarize the implementation of the proposed detector as below:
. We now summarize the implementation of the proposed detector as below:

where  and
and  form the threshold pair, which are set in such a way that the desired
form the threshold pair, which are set in such a way that the desired  is available. Observe that the KRAO-ASB is invariant to the group of transformations given in [26], due to the fact that
is available. Observe that the KRAO-ASB is invariant to the group of transformations given in [26], due to the fact that  can be expressed in terms of the maximal invariant statistic (
can be expressed in terms of the maximal invariant statistic ( ,
,  ). It is thus not surprising that the KRAO-ASB ensures the CFAR property with respect to the disturbance covariance matrix
). It is thus not surprising that the KRAO-ASB ensures the CFAR property with respect to the disturbance covariance matrix  . In what follows, we derive the closed-form expressions for
. In what follows, we derive the closed-form expressions for  and
and  of KRAO-ASB. Given a stochastic representation for
of KRAO-ASB. Given a stochastic representation for  [20]:
[20]:

the  follows to be
follows to be

Note that

Consequently,

where  is pdf of the rv
is pdf of the rv  , and
, and  is the cdf of the rv
is the cdf of the rv  , given
, given  . Then, we consider the standard algebra
. Then, we consider the standard algebra

where  is the positive root to the equation
is the positive root to the equation

and can be obtained via Newton's method. Substituting (32) into (31) and performing some algebra, it yields that
-
(i)
if
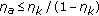 , then
, then 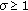
 (34)
(34)namely, the two-stage detector achieves the same performance as that of the KRAO test;
-
(ii)
if
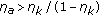 , then
, then 
 (35)
(35)
It is worth noting that there exist an infinite set of infinite triplets ( ) that result in the same
) that result in the same  . Figure 6 shows the contour plots corresponding to different values of
. Figure 6 shows the contour plots corresponding to different values of  , as functions of (
, as functions of ( ) for
) for  ,
,  , and
, and  . It is shown that this detector provides a compromise between the detection and the rejection performance and degenerates to the AMF as
. It is shown that this detector provides a compromise between the detection and the rejection performance and degenerates to the AMF as  , and the KRAO when
, and the KRAO when  . So the appropriate operating point can be selected based on the system requirements.
. So the appropriate operating point can be selected based on the system requirements.
For  hypothesis, the derivation process is similar. In detail, if
hypothesis, the derivation process is similar. In detail, if  ,
,  is the same as for the KRAO test; otherwise, it can be evaluated by
is the same as for the KRAO test; otherwise, it can be evaluated by

where  is the pdf of the rv
is the pdf of the rv  , and
, and  is the cdf of the rv
is the cdf of the rv  , given
, given  .
.
The matched detection performances of the KRAO-ASB, the KRAO, and the AMF are analyzed in Figure 7, with  ,
,  ,
,  , and
, and  . For KRAO-ASB, we show the curve corresponding to the threshold setting that returns the minimum loss with respect to the Kelly's GLRT. The curves highlight that for small-medium SNR values, the KRAO-ASB yields better detection performance than that obtained by performing either the AMF or the KRAO operating alone. We argue that this behavior results from the capability of the KRAO-ASB algorithm in combining information from both single detectors. Similar results for existing two-stage detectors refer to [18–21].
. For KRAO-ASB, we show the curve corresponding to the threshold setting that returns the minimum loss with respect to the Kelly's GLRT. The curves highlight that for small-medium SNR values, the KRAO-ASB yields better detection performance than that obtained by performing either the AMF or the KRAO operating alone. We argue that this behavior results from the capability of the KRAO-ASB algorithm in combining information from both single detectors. Similar results for existing two-stage detectors refer to [18–21].
In Figures 8 and 9, we compare the KRAO-ASB (equipped with  ) to the two-stage detector based on the KWA (KWAS-ASB) [25] (affiliated with
) to the two-stage detector based on the KWA (KWAS-ASB) [25] (affiliated with  ) and the AMF-RAO. The threshold pairs correspond to the most selective case and entail a loss for matched signals of about 1 dB with respect to the Kelly's GLRT at
) and the AMF-RAO. The threshold pairs correspond to the most selective case and entail a loss for matched signals of about 1 dB with respect to the Kelly's GLRT at  and
and  . Figure 8 refers to
. Figure 8 refers to  and
and  , and Figure 9 assumes
, and Figure 9 assumes  and
and  . As it can be seen, the KRAO-ASB exhibits better rejection capabilities of mismatched signals than the KWAS-ASB and the AMF-RAO for the considered system parameters.
. As it can be seen, the KRAO-ASB exhibits better rejection capabilities of mismatched signals than the KWAS-ASB and the AMF-RAO for the considered system parameters.
5. Improved Two-Stage Detector Based on the KRAO
In order to increase the robustness to mismatched signals of the KRAO-ASB, we propose another two-stage detector. This detector is the same as KRAO-ASB, except that the AMF is replaced by a SD. The resulting statistic is

where  is a full-column-rank matrix
is a full-column-rank matrix  . The choice of
. The choice of  makes this detector robust in a homogeneous environment [21]. The vector
makes this detector robust in a homogeneous environment [21]. The vector  is defined as follows:
is defined as follows:

where  is the radar operating wavelength,
is the radar operating wavelength,  is the interelement spacing, and
is the interelement spacing, and  denotes transposition.
denotes transposition.
This detector, which we term Subspace-based and KRAO Adaptive Side lobe Blanker (SKRAO-ASB), can be pictorially described as follows:

where  and
and  form the threshold pair which should be set beforehand to guarantee that the overall desired
form the threshold pair which should be set beforehand to guarantee that the overall desired  is available. We then derive closed-form expressions for
is available. We then derive closed-form expressions for  and
and  of the KRAOS-ASB. First, we replace
of the KRAOS-ASB. First, we replace  with the equivalent decision statistic
with the equivalent decision statistic  . It is shown that the following identities hold for
. It is shown that the following identities hold for  and
and  (see derivation in Appendix):
(see derivation in Appendix):

Then, under  hypothesis [23]:
hypothesis [23]:
-
(i)
given
 and
and  ,
,  is ruled by the complex central F-distribution with 1,
is ruled by the complex central F-distribution with 1,  degrees of freedom, namely,
degrees of freedom, namely, 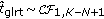 ;
; -
(ii)
 is a complex central F-distribution random variable (rv) with
is a complex central F-distribution random variable (rv) with  ,
, 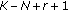 degrees of freedom, namely,
degrees of freedom, namely,  ;
; -
(iii)
 obeys the complex central F-distribution with
obeys the complex central F-distribution with 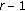 ,
, 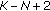 degrees of freedom, namely,
degrees of freedom, namely, 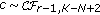 ;
; -
(iv)
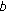 and
and  are statistically independent rv's.
are statistically independent rv's.
Therefore, the  of the SKRAO-ASB can be expressed as
of the SKRAO-ASB can be expressed as

where  ,
,  is the pdf of the rv
is the pdf of the rv  ,
,  is the pdf of the rv
is the pdf of the rv  , and
, and  is the cdf of the rv
is the cdf of the rv  , given
, given  and
and  . As can be seen from (41), the
. As can be seen from (41), the  of the SKRAO-ASB depends on the threshold pairs (
of the SKRAO-ASB depends on the threshold pairs ( ) and the design parameter
) and the design parameter  , as a consequence of which, the SKRAO-ASB possesses the constant false alarm rate (CFAR) property with respect to the disturbance covariance matrix
, as a consequence of which, the SKRAO-ASB possesses the constant false alarm rate (CFAR) property with respect to the disturbance covariance matrix  .
.
For hypothesis  , we assume that the first column of
, we assume that the first column of  is
is  , then perform
, then perform  factorization to
factorization to  :
:

with  being a slice of unitary matrix, namely,
being a slice of unitary matrix, namely,  , and
, and  an invertible upper triangular matrix. Then we define a unitary matrix
an invertible upper triangular matrix. Then we define a unitary matrix  that rotates the
that rotates the  orthonormal columns of
orthonormal columns of  into the first
into the first  elementary vectors, that is,
elementary vectors, that is,

and, in particular,

where  is the
is the  -dimensional column vector whose first entry is equal to one and the remainings are zero. It turns out that the whitened data vector
-dimensional column vector whose first entry is equal to one and the remainings are zero. It turns out that the whitened data vector  is distributed as [28]
is distributed as [28]

where  ,
,  with
with

where  denotes the Euclidean norm of a vector. Then because of the useful signal components, the distributions of
denotes the Euclidean norm of a vector. Then because of the useful signal components, the distributions of  ,
,  and
and  are given in [23]:
are given in [23]:
-
(i)
given
 and
and  ,
,  is ruled by the complex noncentral F-distribution with 1,
is ruled by the complex noncentral F-distribution with 1, 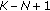 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter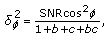 (47)
(47)namely,
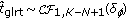 ;
; -
(ii)
 is a complex noncentral F-distribution rv with
is a complex noncentral F-distribution rv with 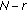 ,
, 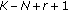 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter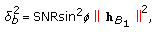 (48)
(48)namely,
 ;
; -
(iii)
given
 ,
,  obeys the complex noncentral F-distribution with
obeys the complex noncentral F-distribution with 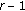 ,
, 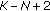 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter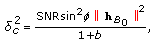 (49)
(49)namely,
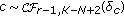 .
.
Now, it is easy to see that the  for the SKRAO-ASB can be expressed as
for the SKRAO-ASB can be expressed as

where  is the pdf of the rv
is the pdf of the rv  ,
,  is the pdf of the rv
is the pdf of the rv  , given
, given  , and
, and  is the cdf of
is the cdf of  , given
, given  and
and  .
.
In Figures 10 and 11, we plot  versus
versus  (measured in degrees) for the SKRAO-ASB and the KRAO-ASB for
(measured in degrees) for the SKRAO-ASB and the KRAO-ASB for  ,
,  ,
,  ,
,  ,
,  , and
, and  . The different curves of each plot refer to different threshold pairs. From Figures 10 and 11, it is clear that the SKRAO-ASB can ensure better robustness with respect to the KRAO-ASB, due to the first stage (the SD), which is less sensitive than the AMF to mismatched signals. It is also clear that, for a given value of
. The different curves of each plot refer to different threshold pairs. From Figures 10 and 11, it is clear that the SKRAO-ASB can ensure better robustness with respect to the KRAO-ASB, due to the first stage (the SD), which is less sensitive than the AMF to mismatched signals. It is also clear that, for a given value of  , the SKRAO-ASB and the KRAO-ASB exhibit the same capability to reject side lobe signals, due to fact that the second stage (the KRAO) is the same.
, the SKRAO-ASB and the KRAO-ASB exhibit the same capability to reject side lobe signals, due to fact that the second stage (the KRAO) is the same.
Finally, we compare the SKRAO-ASB and the KRAO-ASB in terms of computational complexity. We focus on the first stage of each detector, since the second stage of each detector is to be computed only if the fist stage declares a detection. Observe that the AMF does not require the on-line inversion of the matrix  (
( ) and the computation of the extra term
) and the computation of the extra term  , which are necessary to implement the SD decision statistic. It is thus apparent that the KRAO-ASB is faster to implement than the SKRAO-ASB. Anyway, resorting to the usual Landau notation, the SKRAO-ASB involves
, which are necessary to implement the SD decision statistic. It is thus apparent that the KRAO-ASB is faster to implement than the SKRAO-ASB. Anyway, resorting to the usual Landau notation, the SKRAO-ASB involves  floating-point operations (flops), whereas the KRAO-ASB requires
floating-point operations (flops), whereas the KRAO-ASB requires  flops.
flops.
6. Conclusions
In this paper, we consider the problem of adaptive signal detection in the presence of Gaussian noise with unknown covariance matrix. Contributions in this paper are summarized as follows.
-
(i)
We propose a new parametric radar detector, KRAO, by merging the statistics of the Kelly's GLRT test and of the Rao test. We discuss its invariance and CFAR property. We derive the closed-form expressions for the probability of false alarm and the probability of detection in matched and mismatched cases.
-
(ii)
We demonstrate performance of KRAO via simulations. Numerical results show that, with a properly selected value for the design parameter, the proposed KRAO can yield better rejection capabilities of mismatched signals than its counterparts. However, when the sensitivity parameter is greater than or equal to unity, it has a nonnegligible loss for matched signals compared with Kelly's GLRT.
-
(iii)
To compensate the matched detection performance of the KRAO, we propose a two-stage detector consisting of an adaptive matched filter followed by the KRAO. We show that such a two-stage detector has desirable property in terms of selectivity. Its invariance and CFAR property have been studied.
-
(iv)
To increase the robustness of the aforementioned two-stage detector, we introduce another two-stage detector by cascading a GLRT-based subspace detector and the KRAO. It possesses the CFAR property with respect to the unknown covariance matrix of the noise and it can guarantee a wider range of directivity values with respect to aforementioned two-stage detector.
Further work will involve the analysis of the proposed tunable receivers in a partially homogeneous (Gaussian) environment scenario, that is, when the noise covariance matrices of the primary and the secondary data have the same structure but are at different power levels. It is also needed to investigate these tunable receivers in a clutter-dominated non-Gaussian scenario.
References
Kelly EJ: An adaptive detection algorithm. IEEE Transactions on Aerospace and Electronic Systems 1986, 22(2):115-127.
Robey FC, Fuhrmann DR, Kelly EJ, Nitzberg R: A CFAR adaptive matched filter detector. IEEE Transactions on Aerospace and Electronic Systems 1992, 28(1):208-216. 10.1109/7.135446
Greco M, Gini F, Diani M: Robust CFAR detection of random signals in compound-Gaussian clutter plus thermal noise. IEE Proceedings: Radar, Sonar and Navigation 2001, 148(4):227-232. 10.1049/ip-rsn:20010475
Younsi A, Greco M, Gini F, Zoubir AM: Performance of the adaptive generalised matched subspace constant false alarm rate detector in non-Gaussian noise: an experimental analysis. IET Radar, Sonar and Navigation 2009, 3(3):195-202. 10.1049/iet-rsn:20080101
de Maio A, Alfano G, Conte E: Polarization diversity detection in compound-Gaussian clutter. IEEE Transactions on Aerospace and Electronic Systems 2004, 40(1):114-131. 10.1109/TAES.2004.1292147
Shuai X, Kong L, Yang J: Performance analysis of GLRT-based adaptive detector for distributed targets in compound-Gaussian clutter. Signal Processing 2010, 90(1):16-23. 10.1016/j.sigpro.2009.05.008
Conte E, de Maio A, Ricci G: GLRT-based adaptive detection algorithms for range-spread targets. IEEE Transactions on Signal Processing 2001, 49(7):1336-1348. 10.1109/78.928688
de Maio A, Landi L, Farina A: Adaptive radar detection in the presence of mutual coupling and near-field effects. IET Radar, Sonar and Navigation 2008, 2(1):17-24. 10.1049/iet-rsn:20060077
Pulsone NB, Rader CM: Adaptive beamformer orthogonal rejection test. IEEE Transactions on Signal Processing 2001, 49(3):521-529. 10.1109/78.905870
Conte E, Lops M, Ricci G: Asymptotically optimum radar detection in compound-Gaussian clutter. IEEE Transactions on Aerospace and Electronic Systems 1995, 31(2):617-625.
Kraut S, Scharf LL: The CFAR adaptive subspace detector is a scale-invariant GLRT. IEEE Transactions on Signal Processing 1999, 47(9):2538-2541. 10.1109/78.782198
Bandiera F, Besson O, Ricci G: An ABORT-like detector with improved mismatched signals rejection capabilities. IEEE Transactions on Signal Processing 2008, 56(1):14-25.
Bandiera F, Besson O, Orlando D, Ricci G: Theoretical performance analysis of the W-ABORT detector. IEEE Transactions on Signal Processing 2008, 56(5):2117-2121.
Greco M, Gini F, Farina A: Radar detection and classification of jamming signals belonging to a cone class. IEEE Transactions on Signal Processing 2008, 56(5):1984-1993.
de Maio A: Robust adaptive radar detection in the presence of steering vector mismatches. IEEE Transactions on Aerospace and Electronic Systems 2005, 41(4):1322-1337. 10.1109/TAES.2005.1561887
Besson O: Detection of a signal in linear subspace with bounded mismatch. IEEE Transactions on Aerospace and Electronic Systems 2006, 42(3):1131-1139.
Bandiera F, de Maio A, Ricci G: Adaptive CFAR radar detection with conic rejection. IEEE Transactions on Signal Processing 2007, 55(6):2533-2541.
de Maio A: Rao test for adaptive detection in Gaussian interference with unknown covariance matrix. IEEE Transactions on Signal Processing 2007, 55(7):3577-3584.
Richmond CD: Performance of a class of adaptive detection algorithms in nonhomogeneous environments. IEEE Transactions on Signal Processing 2000, 48(5):1248-1262. 10.1109/78.839973
Richmond CD: Performance of the adaptive sidelobe blanker detection algorithm in homogeneous environments. IEEE Transactions on Signal Processing 2000, 48(5):1235-1247. 10.1109/78.839972
Bandiera F, Orlando D, Ricci G: A subspace-based adaptive sidelobe blanker. IEEE Transactions on Signal Processing 2008, 56(9):4141-4151.
Bandiera F, Besson O, Orlando D, Ricci G: A two-stage detector with improved acceptance/rejection capabilities. Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '08), April 2008, Las Vegas, Nev, USA 2301-2304.
Bandiera F, Besson O, Orlando D, Ricci G: An improved adaptive sidelobe blanker. IEEE Transactions on Signal Processing 2008, 56(9):4152-4161.
Kalson SZ: An adaptive array detector with mismatched signal rejection. IEEE Transactions on Aerospace and Electronic Systems 1992, 28(1):195-207. 10.1109/7.135445
Bandiera F, Orlando D, Ricci G: One- and two-stage tunable receivers. IEEE Transactions on Signal Processing 2009, 57(6):2064-2073.
Bose S, Steinhardt AO: Maximal invariant framework for adaptive detection with structured and unstructured covariance matrices. IEEE Transactions on Signal Processing 1995, 43(9):2164-2175. 10.1109/78.414779
Kraut S, Scharf LL, McWhorter LT: Adaptive subspace detectors. IEEE Transactions on Signal Processing 2001, 49(1):1-16. 10.1109/78.890324
Kelly EJ: Adaptive detection in non-stationary interference—part III. MIT, Lincoln Laboratory, Lexington, Mass, USA; August 1987.
Acknowledgments
The authors are very grateful to the anonymous referees for their many helpful comments and constructive suggestions on improving the exposition of this paper. This work was supported by the National Natural Science Foundation of China under Grant no. 60802072.
Author information
Authors and Affiliations
Corresponding author
Appendix
Stochastic Representations of the KRAO and the SD
In this appendix, we come up with suitable stochastic representations for  and
and  . First, we can recast
. First, we can recast  as follows:
as follows:


where  is given by (9). It is shown that
is given by (9). It is shown that  is distributed as a complex noncentral beta rv [28] and can be expressed as the functions of two independent rv's
is distributed as a complex noncentral beta rv [28] and can be expressed as the functions of two independent rv's  and
and  [21], that is,
[21], that is,


It follows that  can be recast as
can be recast as


As to the GLRT-based subspace detector, it is shown that [21]


A deeper discussion on the statistical characterization of  and
and  can be found in [23].
can be found in [23].
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hao, C., Liu, B., Yan, S. et al. Parametric Adaptive Radar Detector with Enhanced Mismatched Signals Rejection Capabilities. EURASIP J. Adv. Signal Process. 2010, 375136 (2010). https://doi.org/10.1155/2010/375136
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/375136
 and
and 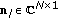 ,
,  , are independent, complex, zero-mean Gaussian vectors with covariance matrix given by
, are independent, complex, zero-mean Gaussian vectors with covariance matrix given by
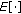 denotes expectation and
denotes expectation and 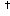 conjugate transposition;
conjugate transposition;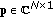 is the unit-norm steering vector of main lobe target echo, which is possibly different from that of the nominal steering vector
is the unit-norm steering vector of main lobe target echo, which is possibly different from that of the nominal steering vector 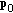 ;
;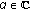 is an unknown deterministic factor which accounts for both target reflectivity and channel effects.
is an unknown deterministic factor which accounts for both target reflectivity and channel effects.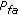 of the KRAO
of the KRAO ,
,  is ruled by the complex central F-distribution with 1,
is ruled by the complex central F-distribution with 1, 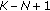 degrees of freedom, namely,
degrees of freedom, namely,  ;
;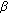 is a complex central beta distribution random variable (rv) with
is a complex central beta distribution random variable (rv) with 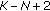 ,
, 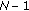 degrees of freedom, namely,
degrees of freedom, namely, 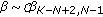 .
.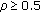 and
and 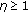
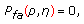
 and
and 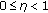

 and
and 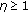
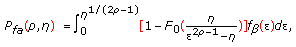
 and
and 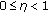


 for the KRAO versus η and ρ with N = 8, K = 24.
for the KRAO versus η and ρ with N = 8, K = 24. of the KRAO
of the KRAO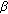 ,
,  is ruled by the complex noncentral F-distribution with 1,
is ruled by the complex noncentral F-distribution with 1,  degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter
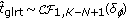 , where
, where 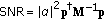 is the total available signal-to-noise ratio;
is the total available signal-to-noise ratio;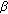 is a complex noncentral beita distribution rv with
is a complex noncentral beita distribution rv with 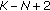 ,
,  degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter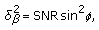
 .
.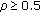 and
and 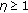
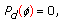
 and
and 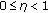

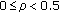 and
and 

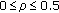 and
and 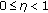





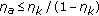 , then
, then 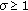

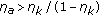 , then
, then 





 and
and  ,
,  is ruled by the complex central F-distribution with 1,
is ruled by the complex central F-distribution with 1,  degrees of freedom, namely,
degrees of freedom, namely, 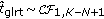 ;
; is a complex central F-distribution random variable (rv) with
is a complex central F-distribution random variable (rv) with  ,
, 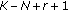 degrees of freedom, namely,
degrees of freedom, namely,  ;
; obeys the complex central F-distribution with
obeys the complex central F-distribution with 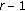 ,
, 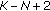 degrees of freedom, namely,
degrees of freedom, namely, 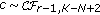 ;
;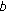 and
and  are statistically independent rv's.
are statistically independent rv's. and
and  ,
,  is ruled by the complex noncentral F-distribution with 1,
is ruled by the complex noncentral F-distribution with 1, 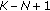 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter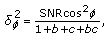
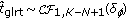 ;
; is a complex noncentral F-distribution rv with
is a complex noncentral F-distribution rv with 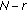 ,
, 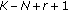 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter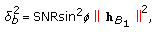
 ;
; ,
,  obeys the complex noncentral F-distribution with
obeys the complex noncentral F-distribution with 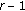 ,
, 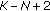 degrees of freedom and noncentrality parameter
degrees of freedom and noncentrality parameter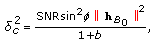
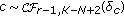 .
.
