Attenuation Analysis of Lamb Waves Using the Chirplet Transform

Abstract

Guided Lamb waves are commonly used in nondestructive evaluation to monitor plate-like structures or to characterize properties of composite or layered materials. However, the dispersive propagation and multimode excitability of Lamb waves complicate their analysis. Advanced signal processing techniques are therefore required to resolve both the time and frequency content of the time-domain wave signals. The chirplet transform (CT) has been introduced as a generalized time-frequency representation (TFR) incorporating more flexibility to adjust the window function to the group delay of the signal when compared to the more classical short-time Fourier transform (STFT). Exploiting this additional degree of freedom, this paper applies an adaptive algorithm based on the CT to calculate mode displacement ratios and attenuation of Lamb waves in elastic plate structures. The CT-based algorithm has a clear performance advantage when calculating mode displacement ratios and attenuation for numerically-simulated Lamb wave signals. For experimental data, the CT retains an advantage over the STFT although measurement noise and parameter uncertainties lead to larger overall deviations from the theoretically expected solutions.

1. Introduction

Ultrasonic waves are often used in nondestructive testing to evaluate the integrity of structural components, as well as to determine material properties of composite or layered materials. In various disciplines such as civil or aerospace engineering, multimode, dispersive guided waves such as Lamb waves have been applied, see Chimenti [1] for an overview. However, complicated signal analysis is the trade off for their versatility. In fact, the main challenges to process Lamb wave signals are due to their very characteristics. Firstly, dispersion phenomena require a resolution of the frequency content of a Lamb wave signal over time which is inherently compromised by the uncertainty principle. Secondly, Lamb waves are multi-modal, which means that interferences between individual modes complicate the allocation of energy and displacement related quantities to a specific mode of excitation. A powerful technique to address these difficulties are time-frequency representations, see for an overview Niethammer et al. [2]. To improve results obtained with conventional methods like the STFT or WT, Hong et al. [3] developed an advanced algorithm based on the STFT using window functions that approximated the group delay of each mode of propagation individually. Kuttig et al. [4] further refined this approach by using the chirplet transform as a generalized TFR, which allows for higher order approximations of the group delay. Encouraged by these advances in signal processing, this paper further explores the potential of CT-based methods for dispersive wave analysis. The problem considered is to extract displacement and energy-related quantities of individual Lamb wave modes in elastic plates, a problem which is relevant for several NDE applications. Variations of the energy associated with a particular mode can for example be used to localize notches in plates by means of a correlation technique, see [5]. Ultrasonic attenuation describes the amplitude decay of wave modes due to energy leakage or the geometry of a specimen. Geometric spreading of Lamb waves in plate structures was examined by Luangvilai et al. [6] using the STFT. Energy leakage in absorbing plates was studied by Luangvilai et al. [7] to determine attenuation coefficients using a refined STFT algorithm. While STFT-based techniques analyze multimode time-domain signals as a whole, the CT-based algorithm uses basis functions specially adjusted to the dispersion relation of each mode of propagation. Physical quantities like displacement or energy can thus be allocated more consistently to individual modes. Since the shaping of the basis functions depends on the knowledge of the dispersion relation for a given set-up, this work considers both numerically simulated ([6]) and experimentally generated ([5]) time-domain signals of Lamb waves in an aluminum plate to evaluate the robustness of the CT-based algorithm as well as its performance.

The paper is organized as follows: first a general definition of the CT is given before describing its use in NDE applications to resolve the time-frequency content of dispersive wave signals by means of an adaptive model-based algorithm. Section 3 contains a description of the candidate NDE problem. The results for mode displacement ratios and geometric spreading of both theoretically and experimentally generated wave signals are presented in Section 4. The concluding remarks of Section 5 outline possibilities to apply the presented technique to other NDE applications.

2. The Chirplet Transform and Its Use in Dispersive Wave Analysis

The chirplet transform has been introduced as a generalized time-frequency representation by Mann and Haykin [8]. The basis function can be adjusted by means of shift, shear, and scaling operators, resulting in a five-dimensional parameter space for the energy density which comprises as projections the respective densities obtained from a short-time Fourier transform (time and frequency shift) and a wavelet transform (time shift and scaling).

2.1. Definition of the Chirplet Transform

The standard definition of the chirplet transform is given by the inner product of a basis function and the signal ,

(1)

where * denotes complex conjugation. The basis function as well as its Fourier transform belongs to a family of chirp signals,

(2)

where the operators , and act in the following manner on the window function or its Fourier transform , respectively,

• Time shift:

  

  (3)

• Frequency shift:

  

  (4)

• Scaling:

  

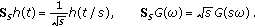  (5)

• Time shear:

  

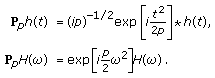  (6)

• Frequency shear:

  

  (7)

Higher order time shear can also be applied resulting in

(8)

and similarly, higher order frequency shear is given by

(9)

The energy density of the chirplet transform at every point in the five dimensional parameter space is given by

(10)

By comparison, the short-time Fourier transform only allows to shift the window function in time and frequency,

(11)

to obtain

(12)

The energy density of the STFT, the spectrogram, is given by

(13)

A more detailed discussion of TFRs used for dispersive wave analysis can be found, for example, in [2].

2.2. Adaptive Algorithm Based on the Chirplet Transform

For ease of visualization, only subspaces of the five-dimensional parameter space of the chirplet transform are considered. In a fashion analogous to the STFT and its energy density representation, the spectrogram, the time-frequency plane is chosen to analyze dispersive waves. According to the definition of the energy density , the squared amplitude of a time-domain signal recording particle displacement is proportional to the energy of the incident Lamb wave, but comprises contributions of all modes of propagation. The objective is to identify energy or displacement related components of individual modes in regions of sufficient mode separation. To that end, the energy content of the time-domain signal is averaged in the time-frequency plane over a region around every point of the dispersion curve of a particular mode using a specially designed window function. In the case of the STFT, time and frequency shift operations result in a region of averaging that approximates the group delay of an individual mode of propagation with zeroth order, whereas the CT-based algorithm as described by Kuttig et al. [4] additionally uses time shearing resulting in higher order approximations. Note that the dispersion curves for a given system depend on the material properties—in the example of a single aluminum plate, its elastic modulus and density as well as its thickness—which determines the robustness of the CT-based algorithm.

For this research, the CT is calculated with a normalized Gaussian window

(14)

with a default value of s. Scaling is 1 by default unless the -isopleths of (14) described by ellipses with half-axis of in time and in frequency intersect with the dispersion curve of another mode. Thus, at least 99.9 of the energy of the window function is concentrated around the mode of interest. The dispersion curves are approximated by a fifth-order polynomial around every point ,

(15)

The group delay of a signal in frequency domain is given by

(16)

The group delay of the window function can thus be fitted to (15) for every mode of propagation by a fifth-order time shear (8) with parameters . Figure 1 depicts the 3-regions of window functions adjusted by the adaptive algorithm for the first symmetrical mode . The CT is not calculated in frequency regions of interference with other modes, for example, around 2 MHz at the intersection of the - and -mode. More details about the adaptive algorithm can be found in [4]. The same Gaussian window function (14) was also used for the STFT-based analysis.

Figure 1

CT basis functions adjusted to the -mode using 5th-order time shear. The dispersion curves are the solution of the Rayleigh-Lamb equations (17) for an aluminum 3003 plate of thickness 0.99 mm and source-receiver distance of 90 mm.

3. Problem Setting

In this paper, Lamb waves traveling in aluminum plate structures are considered. Due to the relatively simple geometry of the plate, it is possible to compute dispersion curves based on the analysis of the Rayleigh-Lamb equations for stress-free boundaries as derived in Achenbach [9],

(17)

where

(18)

and is the plate thickness. The numerical solution of (17) for an aluminum plate is shown in Figure 1 up to frequencies of 10 MHz. The - and - mode are well separated in the frequency ranges 0–1.8 MHz and again between about 2-3 MHz. The same holds for the -mode between 2-3 MHz and 4-5 MHz and for -mode between 3.5–5 MHz, so that the evaluation will be restricted to the first two symmetric () and antisymmetric () modes in these frequency ranges. Consider two different time-domain signals: firstly, numerically simulated data was taken from Luangvilai et al. [6] to have an undisturbed signal for performance evaluation. The authors used normal mode expansion to simulate the out-of-plane displacement field for particles on the plate surface excited by a point-like source for source-receiver distances between 50 mm and 90 mm. Secondly, real measurement data of the out-of-plane velocity field at the surface of an aluminum plate acquired by Benz et al. [5] was available to determine the robustness of the proposed signal processing technique. The experimental setup in this case consisted of an aluminum plate of dimensions 100 mm 100 mm 1 mm and a noncontact, point-like laser measurement and detection system. A laser source was used to generate Lamb waves in the aluminum plate for different source-receiver distances ranging from 50 to 150 mm.

For each of the two data sets, the mode displacement ratios for selective modes are determined as a means to detect material irregularities, for example, for notch localization as in [5]. Apart from that, the amplitude decay over time of individual modes is analyzed as it contains information about the geometry of the specimen. Geometric spreading is given by the quotient for two propagation distances . Such a normalized measure for geometric spreading is chosen since the effect of the excitation source on the energy density will be canceled out.

4. Results

First consider the results obtained for the numerically simulated signal. The particle displacement associated to a particular mode is extracted from the modulus , of each transform. To eliminate the effect of the excitation source, these values are normalized to a particular mode—Table 1 contains the results for normalization with respect to and —by taking the point-by-point quotient of the respective moduli at every frequency . Figure 2 shows the ratio as obtained from the STFT- and CT-based algorithm versus the exact theoretical solution. The latter are very close to the theoretical solution, while the amplitude ratio extracted from the STFT deviates especially at frequencies where individual modes are highly dispersive such as the -mode for frequencies between 2 and 3 MHz. Since the STFT does not use window functions adjusted to the dispersion behavior of individual modes, drastic changes in the group delay can lead to inconsistent values using the STFT, whereas the CT can keep a high level of accuracy.

Table 1 Average deviation from theoretical mode displacement ratio in %.

Figure 2

Out-of-plane displacement ratio of mode normalized to mode for the synthetic signal.

In order to quantify the level of accuracy of each method, a simple metric is introduced that maps a function on a positive real number,

(19)

where and is defined as the inner product for functions [10], . This metric will be used to measure the mean absolute deviation of quantities extracted with the introduced signal processing techniques from the theoretical solution. Note that the adaptive CT-based algorithm only computes energy densities in frequency regions where individual modes are sufficiently separated, that is, when the 3-region of averaging does not intersect with any other mode. The performance measure for both the STFT- and the CT-based method will therefore be restricted to these regions only. Table 1 confirms that the CT-based results for the numerically simulated signal deviates much less from the theoretical solution compared to the ones obtained from the STFT.

A similar observation also holds true when calculating geometric spreading for individual modes. Figure 3 depicts the results for the first antisymmetric mode for frequencies up to 3 MHz. The dashed lines indicate the theoretically expected ratio for different source receiver distances normalized to the longest distance 90 mm. The theoretical solution is compared to the quotient of the moduli , which represent the amplitudes calculated at a frequency for a particluar mode. The CT-based algorithm almost exactly predicts geometric spreading over the frequency range from about 0.3 to 1.5 MHz. In contrast, the STFT results differ from the theoretically expected amplitude decay even in those regions where the -mode is separated. This is confirmed by earlier results of Luangvilai et al. [6] who reported that the amplitude decay due to the propagation pattern cannot be recalculated exactly using the spectrogram. A similar observation can be made for modes , , and as well, that is, the relative error for the CT is up to ten times smaller than the STFT results, c. f. Table 2. Only in frequency regions in which the group delay is almost constant, for example, at about 1-2 MHz for the -mode, both transforms produce similar amplitude ratios. In general, longer propagation distances improve the resolution due to better mode separation in the time-frequency plane.

Table 2 Average deviation in % from theoretical geometric attenuation.

Figure 3

Geometric attenuation for the -mode of the synthetically generated signal determined with the STFT (b) and CT (a). Dashed lines represent the theoretically expected solution , dash-dotted lines are the results obtained from the CT- and STFT-based algorithm, respectively, for the distances 40 mm (pink), 50 mm (green), 60 mm (black), 70 mm (blue), and 80 mm (red) related to 90 mm of propagation distance.

The analysis of the experimentally obtained data yields smaller differences between the two methods as shown by the mean relative deviations from the exact solution for both the mode displacement ratios and geometric spreading, see Tables 1 and 2. The CT produces results closer to the theoretically expected solution, especially if source-receiver distances are large enough as can be seen in Figure 4 when comparing geometric spreading for propagation distances of 50 mm (green curve) and 120 mm (red curve) relative to 150 mm. However, the level of accuracy drops considerably compared to the previous results. The extraction of both displacement and energy related quantities associated with individual modes from a time-frequency representation depends on the dispersion relation, which in turn is determined by the material properties of the specimen. Parameter variations as well as measurement noise therefore influence the accuracy of the STFT-based approach and even more the CT-based algorithm since in the latter case, the basis functions are adjusted for the dispersion, too. When the theoretical dispersion curves are closely matched as for the numerically simulated signal, the performance advantage of the CT-based algorithm becomes apparent.

Figure 4

Geometric attenuation for the -mode of the experimentally generated signal determined with the STFT (b) and CT (a). Dashed lines represent the theoretically expected solution , dash-dotted lines are the results obtained from the CT- and STFT-based algorithm, respectively, for the distances 50 mm (green), 60 mm (black), 90 mm (blue), and 120 mm (red) related to 150 mm of propagation distance.

5. Conclusions

The main goal of this paper is to evaluate the potential of the chirplet transform for dispersive wave analysis. The problem of associating displacement or energy related quantities to individual modes of propagation is of interest in nondestructive evaluation. The theoretical advantage of the proposed method, that is, tailoring regions of averaging to individual modes based on the dispersion relation, becomes apparent when analyzing numerically simulated Lamb wave signals traveling in an aluminum plate. Extracting displacement ratios and geometric spreading for individual modes of propagation succeed with high accuracy in regions with sufficient mode separation. This strongly indicates that the CT-based algorithm can achieve a better performance than more conventional approaches like the spectrogram. The potential to extract displacement and energy-related quantities associated with a particular mode of a dispersive wave therefore qualifies it as a versatile tool in NDE applications. As a model-based approach, the CT based algorithm uses information about the dispersion relation. Since the dispersion relation in turn depends on the material properties and geometry of the specimen, precise knowledge about experimental set-up is a prerequisite to obtain reliable results with this technique. Consequently, the level of accuracy is considerably lower when applied to the experimentally generated data, also for the STFT-based approach. Improving robustness properties as well as algorithmic efficiency remains a goal of future research to make the CT-based technique more easily available and applicable for quantitative nondestructive evaluation.