- Research Article
- Open access
- Published:
Efficient Lookup Table-Based Adaptive Baseband Predistortion Architecture for Memoryless Nonlinearity
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 379249 (2010)
Abstract
Digital predistortion is an effective means to compensate for the nonlinear effects of a memoryless system. In case of a cellular transmitter, a digital baseband predistorter can mitigate the undesirable nonlinear effects along the signal chain, particularly the nonlinear impairments in the radiofrequency (RF) amplifiers. To be practically feasible, the implementation complexity of the predistorter must be minimized so that it becomes a cost-effective solution for the resource-limited wireless handset. This paper proposes optimizations that facilitate the design of a low-cost high-performance adaptive digital baseband predistorter for memoryless systems. A comparative performance analysis of the amplitude and power lookup table (LUT) indexing schemes is presented. An optimized low-complexity amplitude approximation and its hardware synthesis results are also studied. An efficient LUT predistorter training algorithm that combines the fast convergence speed of the normalized least mean squares (NLMSs) with a small hardware footprint is proposed. Results of fixed-point simulations based on the measured nonlinear characteristics of an RF amplifier are presented.
1. Introduction
High-efficiency RF amplifiers have nonlinear amplitude and phase transfer characteristics, which distort the transmitted signals, causing undesired out-of-band spectral regrowth and an increase in error vector magnitude (EVM) and bit error rate (BER). Digital baseband predistortion is an effective means to reconcile the conflicting requirements of linearity and power efficiency. For resource-limited low-cost handsets, the implementation complexity of the predistorter must be minimized. This paper proposes optimizations that facilitate the design of a cost-effective and high-performance adaptive digital baseband predistorter, while minimizing expensive factory calibration requirements. These attributes render this work highly desirable to meet the stringent linearity requirements of the modern third and fourth generation (3G/4G) wireless systems, which employ complex amplitude and phase domain modulations to achieve superior spectral efficiency [1].
While 2.5G EDGE and 3G WCDMA voice waveforms used simpler modulation schemes that exhibited less than  dB of peak-to-average power ratio (PAPR), advanced WCDMA (or HSPA) waveforms exhibit PAPRs in excess of
dB of peak-to-average power ratio (PAPR), advanced WCDMA (or HSPA) waveforms exhibit PAPRs in excess of  dB and modern 4G (LTE, WiMax) use more complex signal constellations resulting in PAPRs of up to 12 dB [1]. Such a high PAPR mandates higher linearity requirements from the RF physical layer, which is in sharp contrast to the stronger demand for increased power efficiency and maximization of the handset battery life. These conflicting requirements can be tamed by resorting to the use of RF front-end amplifiers in their most power-efficient regime, while using signal predistortion schemes to achieve the desired linearity.
dB and modern 4G (LTE, WiMax) use more complex signal constellations resulting in PAPRs of up to 12 dB [1]. Such a high PAPR mandates higher linearity requirements from the RF physical layer, which is in sharp contrast to the stronger demand for increased power efficiency and maximization of the handset battery life. These conflicting requirements can be tamed by resorting to the use of RF front-end amplifiers in their most power-efficient regime, while using signal predistortion schemes to achieve the desired linearity.
The nonlinear gain and phase distortions of RF amplifiers are a strong function of the envelope fluctuations in an RF signal [2, 3]. Consequently, most digital baseband predistorters are implemented as a function of the amplitude of the baseband input. In the case of the complex-gain lookup table (LUT) predistorter [4, 5], the most significant bits (MSBs) of the signal magnitude can be directly used to address the physical memory containing the LUT entries. For example, the first seven MSBs can be used to address an LUT with  entries [6]. The precise amplitude computation requires a square-root operation, which is not directly amenable to efficient hardware implementation, especially at very high processing rates. A square-root approximation proposed in [7] has a performance close to the ideal amplitude calculation. But in addition to the squared magnitude computation, the square-root approximation requires additional LUTs and a linear interpolation calculation. Other practical digital baseband predistorters [4] have been implemented as a function of the instantaneous envelope power
entries [6]. The precise amplitude computation requires a square-root operation, which is not directly amenable to efficient hardware implementation, especially at very high processing rates. A square-root approximation proposed in [7] has a performance close to the ideal amplitude calculation. But in addition to the squared magnitude computation, the square-root approximation requires additional LUTs and a linear interpolation calculation. Other practical digital baseband predistorters [4] have been implemented as a function of the instantaneous envelope power  , where
, where  is the inphase,
is the inphase,  is the quadrature component of the complex baseband signal. The resulting, but often unintended effect, is a concentration of the LUT entries around the higher amplitude region [7, 8]. This power indexing scheme is suitable for class-A and mild class-AB amplifiers since their characteristics are mostly linear until close to saturation. However, this is not well suited to amplifiers with higher power efficiency, such as deep class-AB, class-B, C, and E [9], which exhibit significant nonlinear amplitude and phase distortions across the entire amplitude range. A comparative performance analysis of the amplitude- and power-indexing schemes will be presented in this paper. A suitable low-complexity amplitude approximation for digital baseband predistorters is then applied. The proposed amplitude approximation has lower complexity than the squared magnitude computation and a performance that is close to the ideal amplitude-indexed LUT predistorter.
is the quadrature component of the complex baseband signal. The resulting, but often unintended effect, is a concentration of the LUT entries around the higher amplitude region [7, 8]. This power indexing scheme is suitable for class-A and mild class-AB amplifiers since their characteristics are mostly linear until close to saturation. However, this is not well suited to amplifiers with higher power efficiency, such as deep class-AB, class-B, C, and E [9], which exhibit significant nonlinear amplitude and phase distortions across the entire amplitude range. A comparative performance analysis of the amplitude- and power-indexing schemes will be presented in this paper. A suitable low-complexity amplitude approximation for digital baseband predistorters is then applied. The proposed amplitude approximation has lower complexity than the squared magnitude computation and a performance that is close to the ideal amplitude-indexed LUT predistorter.
Furthermore, the nonlinear characteristics of power amplifiers can display significant variations when the operating temperature fluctuates and as the device ages. To maintain effectiveness of the predistorter and minimize residual distortions as well as calibration requirements, an adaptive predistorter [2, 10] must be used. This problem is further exacerbated by the high PAPR of the modern 3G/4G modulation waveforms. In this paper, an efficient least mean squares (LMS)-based [11] adaptation technique for LUT predistorters is presented as well as its optimization for low complexity hardware implementation.
Section 2 presents a comparative performance analysis between amplitude and power LUT indexing schemes and studies the design and implementation of a suitable amplitude approximation for digital baseband predistorters. Section 3 presents a low-complexity training approach for LUT-based complex-gain predistorters.
2. Performance of Amplitude and Power LUT Indexing
The indexing of a predistorter LUT with the squared signal magnitude is an attractive approach because of the relative ease of computation of  . But it is reported in [7] that the magnitude indexing generally results in significantly better performance for a given LUT size. The performance gap is further exacerbated when the source signal is scaled for the purpose of power control. An LUT-based square-root approximation proposed in [7] has a performance that is close to the ideal amplitude calculation. In this section, we show that an accurate magnitude approximation for digital baseband predistorters, with lower hardware footprint, can be obtained directly from the inphase and quadrature components of the input signal.
. But it is reported in [7] that the magnitude indexing generally results in significantly better performance for a given LUT size. The performance gap is further exacerbated when the source signal is scaled for the purpose of power control. An LUT-based square-root approximation proposed in [7] has a performance that is close to the ideal amplitude calculation. In this section, we show that an accurate magnitude approximation for digital baseband predistorters, with lower hardware footprint, can be obtained directly from the inphase and quadrature components of the input signal.
Simple amplitude approximation techniques have been used for radar detection applications [12–15]. Most of the methods presented result in relatively coarse approximations, even though their precision is within the tolerance of the target applications. But since the digital baseband predistorter is located in the direct transmit path, such large amplitude approximation errors would severely limit the performance of the predistorter, resulting in both residual EVM degradation and spectral distortions.
The general approach to linear amplitude approximation is explained in [13]. It consists of rotating the complex input signal  such that its phase lies in
such that its phase lies in  , then computing a linear combination of the real and imaginary parts of the rotated signal
, then computing a linear combination of the real and imaginary parts of the rotated signal  . The rotated signal
. The rotated signal  is given by
is given by

It can be easily observed that the magnitude of the rotated vector  is equal to the magnitude of the initial vector
is equal to the magnitude of the initial vector  :
:

The approximated amplitude is then obtained by evaluating a linear combination of the real and imaginary parts of  :
:

In [13], the approximation accuracy is improved by further dividing the angular interval  into two intervals, and using two different sets of coefficients
into two intervals, and using two different sets of coefficients  ,
,  that are optimized for their corresponding angular intervals.
that are optimized for their corresponding angular intervals.
This approach can be further extended to arbitrarily improve the approximation accuracy by increasing the number of angular intervals  . If the complex input falls in the
. If the complex input falls in the  th angular interval, the amplitude approximation is given by
th angular interval, the amplitude approximation is given by

where  ,
,  and
and  are the threshold angles delimiting the angular intervals, with
are the threshold angles delimiting the angular intervals, with  and
and  . Figures 1(a) and 1(b) illustrate the use of two and three equal angular intervals, respectively.
. Figures 1(a) and 1(b) illustrate the use of two and three equal angular intervals, respectively.
The amplitude error in the  th angular interval can be computed as
th angular interval can be computed as

The relative amplitude error in the  th interval
th interval  is given by
is given by

The amplitude error (6) is a function of the input angle. The coefficients  must be chosen to minimize a given error metric for each angular interval delimited by the angles
must be chosen to minimize a given error metric for each angular interval delimited by the angles  and
and  . Assuming that the input angle
. Assuming that the input angle  is uniformly distributed, we can obtain a closed-form solution for the coefficients
is uniformly distributed, we can obtain a closed-form solution for the coefficients  that minimizes the mean square of the relative amplitude error
that minimizes the mean square of the relative amplitude error  . The mean squared error
. The mean squared error  can be evaluated as follows:
can be evaluated as follows:

where  . The optimal coefficients are obtained by setting the partial derivatives of
. The optimal coefficients are obtained by setting the partial derivatives of  with respect to the coefficients
with respect to the coefficients  and
and  to zero. Taking the partial derivative of the mean squared error
to zero. Taking the partial derivative of the mean squared error  with respect to the coefficient
with respect to the coefficient  gives
gives

where

Similarly, taking the partial derivative with respect to  gives
gives

with

Setting the partial derivatives to zero yields

It should be noted that since  and
and  , the coefficients
, the coefficients 
 ,
,  and
and  are all strictly positive. The optimal coefficients for the
are all strictly positive. The optimal coefficients for the  th angular interval are obtained by solving the above system of linear equations (12),
th angular interval are obtained by solving the above system of linear equations (12),

with  . For any angular interval delimited by the angles
. For any angular interval delimited by the angles  and
and  , the relatively simple closed-form solution (13) can be evaluated to find the optimal coefficients
, the relatively simple closed-form solution (13) can be evaluated to find the optimal coefficients  in the mean squared error sense. Figure 2 shows the mean squared and peak errors of
in the mean squared error sense. Figure 2 shows the mean squared and peak errors of  as the number of angular intervals is increased from
as the number of angular intervals is increased from  to
to  .
.
These results show that the use of three angular intervals is sufficient to decrease the mean square of the relative amplitude error below  dB. This ensures that there is negligible transmit EVM and ACLR contribution due to the predistorter implementation. As shown by these results, an arbitrary amplitude approximation accuracy can be achieved by selecting a large enough number of angular intervals. But a larger number of angular intervals will result in a more complex decision process and the approximation is useful only if it is amenable to efficient implementation. It should be noted that the optimal coefficients obtained here are based on the assumption that the phase of the input signal is uniformly distributed. This assumption applies very well to most signal modulations. In the special case of a skewed phase probability density, the true optimal coefficients can be better approached using unequal angular intervals.
dB. This ensures that there is negligible transmit EVM and ACLR contribution due to the predistorter implementation. As shown by these results, an arbitrary amplitude approximation accuracy can be achieved by selecting a large enough number of angular intervals. But a larger number of angular intervals will result in a more complex decision process and the approximation is useful only if it is amenable to efficient implementation. It should be noted that the optimal coefficients obtained here are based on the assumption that the phase of the input signal is uniformly distributed. This assumption applies very well to most signal modulations. In the special case of a skewed phase probability density, the true optimal coefficients can be better approached using unequal angular intervals.
For practical implementation, the approximation based on three angular intervals is chosen. The angular intervals are equally spaced. The threshold angles are  , and
, and  . For each input sample
. For each input sample  , the corresponding angular interval is determined by comparing
, the corresponding angular interval is determined by comparing  to
to  since
since  is a monotonic function in the interval
is a monotonic function in the interval 

For efficient hardware implementation, we select  and
and  . The coefficients obtained from (13) are quantized to six bits of resolution. For best results, the quantized coefficients
. The coefficients obtained from (13) are quantized to six bits of resolution. For best results, the quantized coefficients  are used to generate new suboptimal coefficients
are used to generate new suboptimal coefficients  , which are in turn quantized. This two-step process results in a slightly better performance than the direct quantization of the coefficients
, which are in turn quantized. This two-step process results in a slightly better performance than the direct quantization of the coefficients  and
and  . The coefficients and error characteristics of the floating point and quantized amplitude approximations are summarized in Table 1. We observe that the fixed-point approximation has the advantage of being more practical with a smaller hardware footprint, while achieving a performance that is very close to that of the floating-point approximation. Note that the difference in
. The coefficients and error characteristics of the floating point and quantized amplitude approximations are summarized in Table 1. We observe that the fixed-point approximation has the advantage of being more practical with a smaller hardware footprint, while achieving a performance that is very close to that of the floating-point approximation. Note that the difference in  for the floating- versus fixed-point implementation is caused by the round-off errors implemented in the fixed-point hardware.
for the floating- versus fixed-point implementation is caused by the round-off errors implemented in the fixed-point hardware.
The performance of the fixed-point amplitude approximation was simulated within a SIMULINK model of a complete transmitter including predistortion. The amplifier model is based on the extracted AM-AM and AM-PM characteristics of a class-E amplifier [16, 17]. The real and imaginary parts of the class-E amplitude-dependent complex-gain  are shown in Figure 3 or three different temperature settings. The nominal curve at
are shown in Figure 3 or three different temperature settings. The nominal curve at  C is used for the purpose of the present experiment.
C is used for the purpose of the present experiment.
A linearly interpolated complex-gain LUT with  entries was used to predistort the class-E amplifier. A WCDMA rel. 8 HSUPA-compliant 64QAM signal, with
entries was used to predistort the class-E amplifier. A WCDMA rel. 8 HSUPA-compliant 64QAM signal, with  6.5 dB composite PAPR is used as input. The input signal (I/Q) resolution was set to 13 bits and a 3 dB backoff was selected. The EVM and adjacent channel leakage ratios (ACLRs) at 5 MHz offset (ACLR1) and 10 MHz offset (ACLR2) are shown in Table 2. The ACLR1 and ACLR2 are measured in dBc across a 5 MHz channel bandwidth. The EVM resulting from the use of the amplitude indexing is nearly 17 dB lower than that of the power indexing, and only 2 dB higher than that of the ideal amplitude indexing. The ACLR1 and ACLR2 measurements show more than 14 dB improvement when using the amplitude approximation instead of the power indexing. Figure 4 shows the WCDMA power spectral density (PSD) resulting from the above experiment. It is observed that the spectral regrowth is effectively reduced by the predistorters. The higher spectral floor resulting from the power indexing scheme indicates its relatively strong sensitivity to LUT quantization errors.
6.5 dB composite PAPR is used as input. The input signal (I/Q) resolution was set to 13 bits and a 3 dB backoff was selected. The EVM and adjacent channel leakage ratios (ACLRs) at 5 MHz offset (ACLR1) and 10 MHz offset (ACLR2) are shown in Table 2. The ACLR1 and ACLR2 are measured in dBc across a 5 MHz channel bandwidth. The EVM resulting from the use of the amplitude indexing is nearly 17 dB lower than that of the power indexing, and only 2 dB higher than that of the ideal amplitude indexing. The ACLR1 and ACLR2 measurements show more than 14 dB improvement when using the amplitude approximation instead of the power indexing. Figure 4 shows the WCDMA power spectral density (PSD) resulting from the above experiment. It is observed that the spectral regrowth is effectively reduced by the predistorters. The higher spectral floor resulting from the power indexing scheme indicates its relatively strong sensitivity to LUT quantization errors.
The fixed-point coefficients and angular thresholds are chosen to minimize the hardware implementation complexity while maintaining an approximation error close to the optimum. The diagram of Figure 5 illustrates a possible implementation.
This design requires two conditional two's complement operations to implement the  function, three comparators, and four two-to-one multiplexers. The coefficients were chosen to minimize the complexity of the scaling operations. To achieve a fair comparison, the implementation complexity of the amplitude approximation must be compared to that of the instantaneous power computation
function, three comparators, and four two-to-one multiplexers. The coefficients were chosen to minimize the complexity of the scaling operations. To achieve a fair comparison, the implementation complexity of the amplitude approximation must be compared to that of the instantaneous power computation  . Both options were implemented in VHDL and synthesized with the Synopsys Design Compiler. The resulting nand2-equivalent gate count is obtained for different resolutions of the inphase/quadrature components (I/Q). The synthesis results are summarized in Table 3.
. Both options were implemented in VHDL and synthesized with the Synopsys Design Compiler. The resulting nand2-equivalent gate count is obtained for different resolutions of the inphase/quadrature components (I/Q). The synthesis results are summarized in Table 3.
It is clear from these results that the amplitude approximation design results in lower gate count for the input signal resolutions of interest ( 10 bits). The gap between the amplitude-indexing and power-indexing schemes increases rapidly as the resolution is increased from 8 to 14 bits. For input resolutions lower than 8 bits, the power computation results in a slightly lower gate count. But at such low resolutions, the performance is primarily limited by the I/Q signal quantization error. In this case, the resolution of the
10 bits). The gap between the amplitude-indexing and power-indexing schemes increases rapidly as the resolution is increased from 8 to 14 bits. For input resolutions lower than 8 bits, the power computation results in a slightly lower gate count. But at such low resolutions, the performance is primarily limited by the I/Q signal quantization error. In this case, the resolution of the  coefficients can be reduced down to 5 or 4 bits to further reduce the gate count of the amplitude approximation block. Typically, a baseband signal resolution of more than 10 bits is required to meet the close-in spectrum and waveform quality specifications over the entire power control dynamic range as per the standard's requirements. Therefore, the proposed amplitude approximation design has a clear advantage over the power indexing, both in terms of total design area and performance.
coefficients can be reduced down to 5 or 4 bits to further reduce the gate count of the amplitude approximation block. Typically, a baseband signal resolution of more than 10 bits is required to meet the close-in spectrum and waveform quality specifications over the entire power control dynamic range as per the standard's requirements. Therefore, the proposed amplitude approximation design has a clear advantage over the power indexing, both in terms of total design area and performance.
3. Adaptation of Complex-Gain LUT Predistorters
In [4], Cavers proposed the secant update for fast adaptation of complex-gain LUT predistorters. But its high computational complexity makes it unsuitable for hardware implementation.
The indirect learning architecture [18] is illustrated in Figure 6. A replica of the feedforward predistorter is trained in the feedback path as the postinverse of the amplifier nonlinearity. The updated LUT is periodically copied to the feedforward predistorter. This configuration has the advantage of decoupling the transmit path from the update branch. The transmitted signal is therefore isolated from any impulse noise in the feedback path at the cost of replicating the predistorter.
The LUT is an array of  complex-gain entries
complex-gain entries  corresponding to the input amplitudes
corresponding to the input amplitudes  . If the LUT is not interpolated, the
. If the LUT is not interpolated, the  th LUT entry is selected for all feedback signals
th LUT entry is selected for all feedback signals  in the interval defined by
in the interval defined by

For every signal sample  in this interval, an error signal
in this interval, an error signal  is generated,
is generated,

The  th entry
th entry  can be updated using the LMS algorithm as follows:
can be updated using the LMS algorithm as follows:

It should be noted that  is not a holomorphic function and therefore does not have a complex derivative. For the purpose of the steepest-descent algorithm, the complex gradient with respect to the complex gain
is not a holomorphic function and therefore does not have a complex derivative. For the purpose of the steepest-descent algorithm, the complex gradient with respect to the complex gain  can be defined as the combination of the partial derivatives with respect to the real and imaginary parts of
can be defined as the combination of the partial derivatives with respect to the real and imaginary parts of  [19]:
[19]:

where  and
and  , respectively, designate the real and imaginary parts of the argument. Substituting (18) into (17) and carrying out the partial derivatives yields
, respectively, designate the real and imaginary parts of the argument. Substituting (18) into (17) and carrying out the partial derivatives yields

The gradient definition in (18) is equivalent to separately deriving the LMS algorithm for the real and imaginary parts of the complex-gain predistorter, respectively [20]. Considering one single interval at a time allows to simplify the problem by reducing it to finding an approximate inverse of the average amplifier complex gain within the considered interval. For each incoming feedback sample, only the corresponding entry that is addressed by its magnitude is updated. This process is similar to the partial update LMS [21, 22]. The update operation requires two complex multiplies (one to compute the error  and one to evaluate the gradient), two additions and the scaling by
and one to evaluate the gradient), two additions and the scaling by  , which can be simplified if it is restricted to powers of two. The update system is stable provided that
, which can be simplified if it is restricted to powers of two. The update system is stable provided that  [23], with
[23], with  being equal to
being equal to  for all
for all  falling in the
falling in the  th interval. If the LUT size is large, the samples
th interval. If the LUT size is large, the samples  can be assumed to have a uniform distribution across the interval. In this case, the expectation can be approximated by the square of the average magnitude, which is the point located at the center of the interval:
can be assumed to have a uniform distribution across the interval. In this case, the expectation can be approximated by the square of the average magnitude, which is the point located at the center of the interval:  .
.
If the regular LMS update equation (19) is used, the convergence speed will vary across the table entries. The upper entries will converge significantly faster than the lower entries. To avoid this issue, the normalized LMS (NLMS) algorithm [24, 25] can be used,

The NLMS update of (20) results in faster and uniform convergence of the entries across the LUT. But its direct implementation has two limitations.
-
(i)
For very low values of
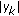 the system becomes susceptible to noise in the feedback path, with a potential to drive the update system into instability.
the system becomes susceptible to noise in the feedback path, with a potential to drive the update system into instability. -
(ii)
The scaling by the magnitude is an expensive operation that is not directly amenable to efficient hardware implementation.
An approximation of the NLMS similar to the clipped LMS algorithm [26–28] is proposed. This approach, termed low-complexity normalized LMS (LCNLMS), is suitable for efficient hardware implementation and maintains the fast convergence of the NLMS. First, the update equation of (20) can be conveniently reformulated as follows:

where  is the complex argument of
is the complex argument of  and
and  . It is clear from this incremental update that the NLMS is equivalent to using a variable update coefficient that is inversely proportional to the input amplitude
. It is clear from this incremental update that the NLMS is equivalent to using a variable update coefficient that is inversely proportional to the input amplitude  and replacing the complex multiply with a rotation of the error by
and replacing the complex multiply with a rotation of the error by  . The computational complexity of the rotation operation can be greatly simplified by quantizing the angle
. The computational complexity of the rotation operation can be greatly simplified by quantizing the angle  . To do so, let us define the sign function
. To do so, let us define the sign function  corresponding to the sign bit in the two's complement representation as
corresponding to the sign bit in the two's complement representation as

Let  and
and  , respectively, be the signs of the real and imaginary parts of the feedback signal
, respectively, be the signs of the real and imaginary parts of the feedback signal  ,
,

Quantization of the angle  can be achieved by using the following update equation:
can be achieved by using the following update equation:

with

The phase  is therefore quantized to four possible values, that is,
is therefore quantized to four possible values, that is,  , thus effectively eliminating one complex multiplier (or four real multipliers).
, thus effectively eliminating one complex multiplier (or four real multipliers).
The amplitude-dependent coefficient  could be implemented as a lookup table with one coefficient per table entry. To minimize the required memory space and further reduce the implementation costs,
could be implemented as a lookup table with one coefficient per table entry. To minimize the required memory space and further reduce the implementation costs,  can be constrained to powers of two and generated from the magnitude
can be constrained to powers of two and generated from the magnitude  as follows:
as follows:

where  stands for the
stands for the  rounding function (round to the nearest integer towards infinity) and
rounding function (round to the nearest integer towards infinity) and  is an arbitrary integer. In the above expression, it is assumed without loss of generality that the signal is normalized such that
is an arbitrary integer. In the above expression, it is assumed without loss of generality that the signal is normalized such that  . Forcing the maximum exponent to
. Forcing the maximum exponent to  sets a maximum value for
sets a maximum value for  to prevent any instability caused by the sensitivity to noise at low amplitudes. The base-two exponent
to prevent any instability caused by the sensitivity to noise at low amplitudes. The base-two exponent  can be very efficiently generated with the simple combinatorial circuit illustrated in Figure 7. The amplitude is represented with
can be very efficiently generated with the simple combinatorial circuit illustrated in Figure 7. The amplitude is represented with  bits of resolution and the exponent
bits of resolution and the exponent  is represented with a three-bit binary word. This is equivalent to setting
is represented with a three-bit binary word. This is equivalent to setting  . The first stage of the circuit outputs a one-hot binary vector (i.e., only one bit is set at a time) corresponding to the position of highest nonzero amplitude bit. The second stage encodes the position of the nonzero bit into a binary number, effectively computing a rounded base-two logarithm of the input amplitude. The scaling by
. The first stage of the circuit outputs a one-hot binary vector (i.e., only one bit is set at a time) corresponding to the position of highest nonzero amplitude bit. The second stage encodes the position of the nonzero bit into a binary number, effectively computing a rounded base-two logarithm of the input amplitude. The scaling by  can be implemented by a simple binary shifter.
can be implemented by a simple binary shifter.
The combinatorial logic implementation of the amplitude-dependent update coefficient lacks flexibility since the update speed cannot be changed. This issue can be tackled by introducing an additional coefficient  that is programmable,
that is programmable,

It should be noted that this low complexity update is even simpler to realize in hardware than the regular LMS, which requires two complex multipliers and has a much slower convergence speed.
This low-complexity update method (LCNLMS) was simulated and compared to the LMS and the NLMS. The previously described class-E amplifier is used in this experiment and a 10 MHz LTE signal with a composite PAPR of 8.5 dB is used to train the feedback LUT in the indirect learning setup. The size of the complex-gain LUTs is set to  entries. The complex-gain LUT entries are initially set to unity, which is functionally equivalent to bypassing the predistorter. The resolution of the inphase and quadrature (I/Q) signal components is set to 13 bits. To measure the sensitivity of the adaptation to noise, the feedback signal is corrupted by additive white Gaussian noise (AWGN) and has an SNR of 33 dB. The LUT is updated at a rate of 30.76 MHz and the overall simulation was run at a sampling rate of 61.52 MHz. The update coefficient
entries. The complex-gain LUT entries are initially set to unity, which is functionally equivalent to bypassing the predistorter. The resolution of the inphase and quadrature (I/Q) signal components is set to 13 bits. To measure the sensitivity of the adaptation to noise, the feedback signal is corrupted by additive white Gaussian noise (AWGN) and has an SNR of 33 dB. The LUT is updated at a rate of 30.76 MHz and the overall simulation was run at a sampling rate of 61.52 MHz. The update coefficient  for LMS and NMLS is set to
for LMS and NMLS is set to  . Comparing (21) and (24) shows that the LCNLMS intrinsically increases the update rate by a factor of
. Comparing (21) and (24) shows that the LCNLMS intrinsically increases the update rate by a factor of  . On the other hand, the biased quantization of
. On the other hand, the biased quantization of  in (26) approximately compensates for this factor. Therefore, setting
in (26) approximately compensates for this factor. Therefore, setting  for the LCNLMS ensures a fair comparison.
for the LCNLMS ensures a fair comparison.
Figure 8 compares the convergence of the regular LMS, the NLMS, and the proposed LCNLMS. It shows the instantaneous mean squared error  between the updated LUT
between the updated LUT  and an optimal reference LUT
and an optimal reference LUT  obtained via least-square approximations in each interval
obtained via least-square approximations in each interval

These results show that the convergence speed of the proposed LCNLMS is close to that of the NLMS. It should also be noted that the LCNLMS leads to an implementation complexity even lower than the generic LMS.
The adaptation was disabled after 5 ms and the trained LUT was used in the feedforward path. The resulting output PSDs are shown in Figure 9. The LCNLMS has the same performance as the NLMS. Despite the relatively long training time, the lower entries of the LMS-trained LUT did not converge, which explains the poor performance compared to the NLMS and LCNLMS.
3.1. Updating a Linearly-Interpolated LUT
Linear interpolation greatly reduces the LUT approximation errors and enables significant reduction of the required LUT size [6, 29]. If linear interpolation is used, for each feedback sample magnitude  falling between addresses
falling between addresses  and
and  , the interpolated complex-gain is
, the interpolated complex-gain is

where  is the interpolation factor. For the purpose of practical implementation, the address
is the interpolation factor. For the purpose of practical implementation, the address  and the interpolation factor
and the interpolation factor  are readily obtained from the amplitude bits
are readily obtained from the amplitude bits

It should be noted that for each input sample, two consecutive LUT entries must be fetched from memory and interpolated to compute the complex-gain. The hardware implementation and the sequencing of operations can be greatly simplified by using a dual-port memory. In general, dual-port memories are more expensive and larger in size than single-port memories of the same capacity. But in the case of the LUT interpolation, the two entries to be fetched are always located at consecutive addresses. Consequently, a dual-port memory of size  can be emulated using two single-port memory blocks of size
can be emulated using two single-port memory blocks of size  and simple additional logic. One of the blocks stores the entries located at even addresses, and the other one stores the entries at odd addresses. This process allows the implementation of a pseudo dual-port memory at the same cost as a single-port memory. The only limitation is that simultaneous read/write operations require one address to be odd and the other to be even. In the case of a linearly interpolated LUT, this requirement is always satisfied because the addresses
and simple additional logic. One of the blocks stores the entries located at even addresses, and the other one stores the entries at odd addresses. This process allows the implementation of a pseudo dual-port memory at the same cost as a single-port memory. The only limitation is that simultaneous read/write operations require one address to be odd and the other to be even. In the case of a linearly interpolated LUT, this requirement is always satisfied because the addresses  and
and  are consecutive. If linear interpolation is used in the feedback path (or updated LUT), the error signal
are consecutive. If linear interpolation is used in the feedback path (or updated LUT), the error signal  is given by
is given by

Since two entries are used to generate the interpolated complex-gain, both entries should be updated with each new data sample. The application of the same LMS algorithm by alternatively computing the gradients with respect to  and
and  results in the following update equations:
results in the following update equations:

Similarly to (27), the LCNLMS can also be applied to the linearly interpolated case, leading to the following update equations:

Figure 10 shows that both the nearest neighbor and linear interpolation adaptations converge to the same solution. For the same update coefficient  , the linearly interpolated adaptation has lower LUT approximation errors and therefore, results in a slightly better steady state performance. The steady state performance of the nearest neighbor adaptation can generally be improved by decreasing the update coefficient, at the cost of slower convergence.
, the linearly interpolated adaptation has lower LUT approximation errors and therefore, results in a slightly better steady state performance. The steady state performance of the nearest neighbor adaptation can generally be improved by decreasing the update coefficient, at the cost of slower convergence.
Figure 11 uses a 4G LTE 10 MHz single-carrier (orthogonal) frequency-division multiple access (SC-FDMA) input stimulus with greater than 8.5 dB of composite PAPR to illustrate the resulting signal PSDs using the nearest neighbor and the linearly interpolated adaptation schemes. The simulation setup described in the previous section was reused, where the root mean square level of the digital signal was adjusted to account for the higher PAPR of the modulation waveform. The feedforward predistorter is linearly interpolated in both cases and the update coefficient is set to  . It is evident that the close-in performances achieved using either scheme are quite comparable. The spectral regrowth is significantly reduced. The spectral floor using ZOH is 2 to 3 dB higher due to the intrinsic half-bit excess quantization noise of the ZOH as compared to the linear interpolation [29].
. It is evident that the close-in performances achieved using either scheme are quite comparable. The spectral regrowth is significantly reduced. The spectral floor using ZOH is 2 to 3 dB higher due to the intrinsic half-bit excess quantization noise of the ZOH as compared to the linear interpolation [29].
Therefore, even when the feedforward predistorter is chosen to be linearly interpolated, the nearest neighbor adaptation can be used in the update branch of the indirect learning architecture, without much performance penalty. Note that ZOH requires only one memory read and write for each data sample. On the other hand, the linearly interpolated adaptation requires two memory reads and writes per data sample, placing more stringent timing requirements on the adaptation hardware.
4. Conclusions
In this paper, an efficient LUT-based adaptive memoryless predistorter configuration, with minimized chip area, has been presented. An amplitude approximation scheme suitable for digital baseband predistorters is proposed. A closed-form solution is derived to determine the optimal parameters for the amplitude approximation using any arbitrary angular interval size. A quantized amplitude approximation with three angular intervals is implemented in VHDL and synthesized with the SYNOPSYS DESIGN COMPILER. The predistorter performance using the proposed area-efficient scheme is shown to be within  dB of the ideal amplitude performance, while it outperforms the power-indexing in both design area and rejection of residual distortions by a wide margin.
dB of the ideal amplitude performance, while it outperforms the power-indexing in both design area and rejection of residual distortions by a wide margin.
An adaptation algorithm for complex-gain LUT predistorters based on the indirect learning architecture is also presented. The proposed adaptation algorithm has been optimized for efficient hardware implementation. It has a convergence speed that is comparable to the normalized LMS and lends itself to very efficient hardware implementation. The proposed optimized adaptive predistorter can be extended to mitigate memory effects by adding a linear time-invariant filter in cascade with the memoryless complex-gain predistorter [5, 30].
References
3rd Generation Partnership Project (3GPP), March 2010, http://www.3gpp.org/
de Figueiredo RJP, Fang L, Lee BM: Design of an adaptivepredistorter for solid state power amplifier in wireless OFDM systems. Research Letters in Signal Processing 2009, 2009:-5.
Waheed K, Ba SN: Adaptive digital linearization of a DRP based EDGE transmitter for cellular handsets. Proceedings of the 50th IEEE International Midwest Symposium on Circuits and Systems (MWCSAS '07), August 2007 706-709.
Cavers JK: Amplifier linearization using a digital predistorter with fast adaptation and low memory requirements. IEEE Transactions on Vehicular Technology 1990, 39(4):374-382. 10.1109/25.61359
Jardin P, Baudoin G: Filter lookup table method for power amplifier linearization. IEEE Transactions on Vehicular Technology 2007, 56(3):1076-1087.
Ba SN, Waheed K, Zhou GT: Efficient spacing scheme for a linearly interpolated lookup table predistorter. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '08), May 2008 1512-1515.
Sundström L, Faulkner M, Johansson M: Quantization analysis and design of a digital predistortion linearizer for RF power amplifiers. IEEE Transactions on Vehicular Technology 1996, 45(4):707-719. 10.1109/25.543741
Cavers JK: Optimum table spacing in predistorting amplifier linearizers. IEEE Transactions on Vehicular Technology 1999, 48(5):1699-1705. 10.1109/25.790551
Kenington PB: High Linearity RF Amplifier Design. Artech House Publishers, Norwood, Mass, USA; 2000.
Lee KC, Gardner P: Comparison of different adaptation algorithms for adaptive digital predistortion based on EDGE standard. Proceedings of IEEE MTT-S International Microwave Symposium Digest, May 2001 2: 1353-1356.
Widrow B, Stearns S: Adaptive Signal Processing. Prentice Hall, Englewood Cliffs, NJ, USA; 1985.
Onoe M: Fast amplitude approximation yielding either exact meanor minimum deviation for quadrature pairs. Proceedings of the IEEE 1972, 60(7):921-922.
Filip AE: A baker's dozen magnitude approximations and their detection statistics. IEEE Transactions on Aerospace and Electronic Systems 1976, 12(1):86-89.
Braun F, Blaser H: Digital hardware for approximating the amplitude of quadrature pairs. Electronics Letters 1974, 10(13):255-256. 10.1049/el:19740201
Filip AE:Linear approximations to
 having equiripple error characteristics. IEEE Trans Audio Electroacoust 1973, AU-21(6):554-556.
having equiripple error characteristics. IEEE Trans Audio Electroacoust 1973, AU-21(6):554-556.Tsou WA, Wuen WS, Yang TY, Wen KA: Analysis and compensation of the AM-AM and AM-PM distortion for CMOS cascode class-E power amplifier. International Journal of Microwave Science and Technology 2009, 2009:-9.
Cruise P, Hung C-M, Staszewski RB, Eliezer O, Rezeq S, Maggio K, Leipold D: A digital-to-RF-amplitude converter for GSM/GPRS/EDGE in 90-nm digital CMOS. Proceedings of IEEE Radio Frequency Integrated Circuits Symposium (RFIC '05), June 2005 RMO1A-4: 21-24.
Eun C, Powers EJ: A new volterra predistorter based on the indirect learning architecture. IEEE Transactions on Signal Processing 1997, 45(1):223-227. 10.1109/78.552219
Brandwood DH: A complex gradient operator and its application in adaptive array theory. IEE Proceedings F 1983, 130(1):11-16. 10.1049/ip-f-1.1983.0003
Widrow B, McCool J, Ball M: The complex LMS algorithm. Proceedings of the IEEE 1975, 63(4):719-720.
Douglas SC: Adaptive filters employing partial updates. IEEE Transactions on Circuits and Systems II 1997, 44(3):209-216. 10.1109/82.558455
Ramos P, Torrubia R, López A, Salinas A, Masgrau E: Step size bound of the sequential partial update LMS algorithm with periodic input signals. EURASIP Journal on Audio, Speech, and Music Processing 2007, 2007:-15.
Widrow B, Walach E: On the statistical efficiency of the LMS algorithm with nonstationary inputs. IEEE Transactions on Information Theory 1984, 30(2):211-221. 10.1109/TIT.1984.1056892
Goodwin GC, Sin KS: Adaptive Filtering Prediction and Control. Prentice Hall, Englewood Cliffs, NJ, USA; 1984.
Aboulnasr T, Mayyas K: Complexity reduction of the NLMS algorithm via selective coefficient update. IEEE Transactions on Signal Processing 1999, 47(5):1421-1424. 10.1109/78.757235
Moschner JL: Adaptive filtering with clipped input data, Ph.D. dissertation. Stanford University, Stanford, Calif, USA; June 1970.
Lotfizad M, Yazdi HS: Modified clipped LMS algorithm. EURASIP Journal on Applied Signal Processing 2005, 2005(8):1229-1234. 10.1155/ASP.2005.1229
Crum L, Wu S: Convergence of the quantizing learning method forsystem identification. IEEE Transactions on Automatic Control 1968, 13(3):297-298.
Ba SN, Waheed K, Zhou GT: Optimal spacing of a linearlyinterpolated complex-gain LUT predistorter. IEEE Transactions onVehicular Technology 2010, 59(2):673-681.
Ding L, Raich R, Zhou GT: A hammerstein predistortion linearization design based on the indirect learning architecture. Proceedings of IEEE International Conference on Acoustic, Speech, and Signal Processing (ICASSP '02), May 2002 3:
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ba, S.N., Waheed, K. & Zhou, G.T. Efficient Lookup Table-Based Adaptive Baseband Predistortion Architecture for Memoryless Nonlinearity. EURASIP J. Adv. Signal Process. 2010, 379249 (2010). https://doi.org/10.1155/2010/379249
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/379249






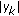 the system becomes susceptible to noise in the feedback path, with a potential to drive the update system into instability.
the system becomes susceptible to noise in the feedback path, with a potential to drive the update system into instability.




 having equiripple error characteristics. IEEE Trans Audio Electroacoust 1973, AU-21(6):554-556.
having equiripple error characteristics. IEEE Trans Audio Electroacoust 1973, AU-21(6):554-556.