- Review Article
- Open access
- Published:
A Review on Spectrum Sensing for Cognitive Radio: Challenges and Solutions
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 381465 (2010)
Abstract
Cognitive radio is widely expected to be the next Big Bang in wireless communications. Spectrum sensing, that is, detecting the presence of the primary users in a licensed spectrum, is a fundamental problem for cognitive radio. As a result, spectrum sensing has reborn as a very active research area in recent years despite its long history. In this paper, spectrum sensing techniques from the optimal likelihood ratio test to energy detection, matched filtering detection, cyclostationary detection, eigenvalue-based sensing, joint space-time sensing, and robust sensing methods are reviewed. Cooperative spectrum sensing with multiple receivers is also discussed. Special attention is paid to sensing methods that need little prior information on the source signal and the propagation channel. Practical challenges such as noise power uncertainty are discussed and possible solutions are provided. Theoretical analysis on the test statistic distribution and threshold setting is also investigated.
1. Introduction
It was shown in a recent report [1] by the USA Federal Communications Commission (FCC) that the conventional fixed spectrum allocation rules have resulted in low spectrum usage efficiency in almost all currently deployed frequency bands. Measurements in other countries also have shown similar results [2]. Cognitive radio, first proposed in [3], is a promising technology to fully exploit the under-utilized spectrum, and consequently it is now widely expected to be the next Big Bang in wireless communications. There have been tremendous academic researches on cognitive radios, for example, [4, 5], as well as application initiatives, such as the IEEE 802.22 standard on wireless regional area network (WRAN) [6, 7] and the Wireless Innovation Alliance [8] including Google and Microsoft as members, which advocate to unlock the potential in the so-called "White Spaces" in the television (TV) spectrum. The basic idea of a cognitive radio is spectral reusing or spectrum sharing, which allows the secondary networks/users to communicate over the spectrum allocated/licensed to the primary users when they are not fully utilizing it. To do so, the secondary users are required to frequently perform spectrum sensing, that is, detecting the presence of the primary users. Whenever the primary users become active, the secondary users have to detect the presence of them with a high probability and vacate the channel or reduce transmit power within certain amount of time. For example, for the upcoming IEEE 802.22 standard, it is required for the secondary users to detect the TV and wireless microphone signals and vacant the channel within two seconds once they become active. Furthermore, for TV signal detection, it is required to achieve 90% probability of detection and 10% probability of false alarm at signal-to-noise ratio (SNR) level as low as  dB.
dB.
There are several factors that make spectrum sensing practically challenging. First, the required SNR for detection may be very low. For example, even if a primary transmitter is near a secondary user (the detection node), the transmitted signal of the primary user can be deep faded such that the primary signal's SNR at the secondary receiver is well below  dB. However, the secondary user still needs to detect the primary user and avoid using the channel because it may strongly interfere with the primary receiver if it transmits. A practical scenario of this is a wireless microphone operating in TV bands, which only transmits with a power less than 50 mW and a bandwidth less than 200 KHz. If a secondary user is several hundred meters away from the microphone device, the received SNR may be well below
dB. However, the secondary user still needs to detect the primary user and avoid using the channel because it may strongly interfere with the primary receiver if it transmits. A practical scenario of this is a wireless microphone operating in TV bands, which only transmits with a power less than 50 mW and a bandwidth less than 200 KHz. If a secondary user is several hundred meters away from the microphone device, the received SNR may be well below  dB. Secondly, multipath fading and time dispersion of the wireless channels complicate the sensing problem. Multipath fading may cause the signal power to fluctuate as much as
dB. Secondly, multipath fading and time dispersion of the wireless channels complicate the sensing problem. Multipath fading may cause the signal power to fluctuate as much as  dB. On the other hand, unknown time dispersion in wireless channels may turn the coherent detection unreliable. Thirdly, the noise/interference level may change with time and location, which yields the noise power uncertainty issue for detection [9–12].
dB. On the other hand, unknown time dispersion in wireless channels may turn the coherent detection unreliable. Thirdly, the noise/interference level may change with time and location, which yields the noise power uncertainty issue for detection [9–12].
Facing these challenges, spectrum sensing has reborn as a very active research area over recent years despite its long history. Quite a few sensing methods have been proposed, including the classic likelihood ratio test (LRT) [13], energy detection (ED) [9, 10, 13, 14], matched filtering (MF) detection [10, 13, 15], cyclostationary detection (CSD) [16–19], and some newly emerging methods such as eigenvalue-based sensing [6, 20–25], wavelet-based sensing [26], covariance-based sensing [6, 27, 28], and blindly combined energy detection [29]. These methods have different requirements for implementation and accordingly can be classified into three general categories: (a) methods requiring both source signal and noise power information, (b) methods requiring only noise power information (semiblind detection), and (c) methods requiring no information on source signal or noise power (totally blind detection). For example, LRT, MF, and CSD belong to category A; ED and wavelet-based sensing methods belong to category B; eigenvalue-based sensing, covariance-based sensing, and blindly combined energy detection belong to category C. In this paper, we focus on methods in categories B and C, although some other methods in category A are also discussed for the sake of completeness. Multiantenna/receiver systems have been widely deployed to increase the channel capacity or improve the transmission reliability in wireless communications. In addition, multiple antennas/receivers are commonly used to form an array radar [30, 31] or a multiple-input multiple-output (MIMO) radar [32, 33] to enhance the performance of range, direction, and/or velocity estimations. Consequently, MIMO techniques can also be applied to improve the performance of spectrum sensing. Therefore, in this paper we assume a multi-antenna system model in general, while the single-antenna system is treated as a special case.
When there are multiple secondary users/receivers distributed at different locations, it is possible for them to cooperate to achieve higher sensing reliability. There are various sensing cooperation schemes in the current literature [34–44]. In general, these schemes can be classified into two categories: (A) data fusion: each user sends its raw data or processed data to a specific user, which processes the data collected and then makes the final decision; (B) decision fusion: multiple users process their data independently and send their decisions to a specific user, which then makes the final decision.
In this paper, we will review various spectrum sensing methods from the optimal LRT to practical joint space-time sensing, robust sensing, and cooperative sensing and discuss their advantages and disadvantages. We will pay special attention to sensing methods with practical application potentials. The focus of this paper is on practical sensing algorithm designs; for other aspects of spectrum sensing in cognitive radio, the interested readers may refer to other resources like [45–52].
The rest of this paper is organized as follows. The system model for the general setup with multiple receivers for sensing is given in Section 2. The optimal LRT-based sensing due to the Neyman-Pearson theorem is reviewed in Section 3. Under some special conditions, it is shown that the LRT becomes equivalent to the estimator-correlator detection, energy detection, or matched filtering detection. The Bayesian method and the generalized LRT for sensing are discussed in Section 4. Detection methods based on the spatial correlations among multiple received signals are discussed in Section 5, where optimally combined energy detection and blindly combined energy detection are shown to be optimal under certain conditions. Detection methods combining both spatial and time correlations are reviewed in Section 6, where the eigenvalue-based and covariance-based detections are discussed in particular. The cyclostationary detection, which exploits the statistical features of the primary signals, is reviewed in Section 7. Cooperative sensing is discussed in Section 8. The impacts of noise uncertainty and noise power estimation to the sensing performance are analyzed in Section 9. The test statistic distribution and threshold setting for sensing are reviewed in Section 10, where it is shown that the random matrix theory is very useful for the related study. The robust spectrum sensing to deal with uncertainties in source signal and/or noise power knowledge is reviewed in Section 11, with special emphasis on the robust versions of LRT and matched filtering detection methods. Practical challenges and future research directions for spectrum sensing are discussed in Section 12. Finally, Section 13 concludes the paper.
2. System Model
We assume that there are  antennas at the receiver. These antennas can be sufficiently close to each other to form an antenna array or well separated from each other. We assume that a centralized unit is available to process the signals from all the antennas. The model under consideration is also applicable to the multinode cooperative sensing [34–44, 53], if all nodes are able to send their observed signals to a central node for processing. There are two hypotheses:
antennas at the receiver. These antennas can be sufficiently close to each other to form an antenna array or well separated from each other. We assume that a centralized unit is available to process the signals from all the antennas. The model under consideration is also applicable to the multinode cooperative sensing [34–44, 53], if all nodes are able to send their observed signals to a central node for processing. There are two hypotheses:  , signal absent, and
, signal absent, and  , signal present. The received signal at antenna/receiver
, signal present. The received signal at antenna/receiver  is given by
is given by

In hypothesis  ,
,  is the received source signal at antenna/receiver
is the received source signal at antenna/receiver  , which may include the channel multipath and fading effects. In general,
, which may include the channel multipath and fading effects. In general,  can be expressed as
can be expressed as

where  denotes the number of primary user/antenna signals,
denotes the number of primary user/antenna signals,  denotes the transmitted signal from primary user/antenna
denotes the transmitted signal from primary user/antenna  ,
,  denotes the propagation channel coefficient from the
denotes the propagation channel coefficient from the  th primary user/antenna to the
th primary user/antenna to the  th receiver antenna, and
th receiver antenna, and  denotes the channel order for
denotes the channel order for  . It is assumed that the noise samples
. It is assumed that the noise samples  's are independent and identically distributed (i.i.d) over both
's are independent and identically distributed (i.i.d) over both  and
and  . For simplicity, we assume that the signal, noise, and channel coefficients are all real numbers.
. For simplicity, we assume that the signal, noise, and channel coefficients are all real numbers.
The objective of spectrum sensing is to make a decision on the binary hypothesis testing (choose  or
or  ) based on the received signal. If the decision is
) based on the received signal. If the decision is  , further information such as signal waveform and modulation schemes may be classified for some applications. However, in this paper, we focus on the basic binary hypothesis testing problem. The performance of a sensing algorithm is generally indicated by two metrics: probability of detection,
, further information such as signal waveform and modulation schemes may be classified for some applications. However, in this paper, we focus on the basic binary hypothesis testing problem. The performance of a sensing algorithm is generally indicated by two metrics: probability of detection,  , which defines, at the hypothesis
, which defines, at the hypothesis  , the probability of the algorithm correctly detecting the presence of the primary signal; and probability of false alarm,
, the probability of the algorithm correctly detecting the presence of the primary signal; and probability of false alarm,  , which defines, at the hypothesis
, which defines, at the hypothesis  , the probability of the algorithm mistakenly declaring the presence of the primary signal. A sensing algorithm is called "optimal" if it achieves the highest
, the probability of the algorithm mistakenly declaring the presence of the primary signal. A sensing algorithm is called "optimal" if it achieves the highest  for a given
for a given  with a fixed number of samples, though there could be other criteria to evaluate the performance of a sensing algorithm.
with a fixed number of samples, though there could be other criteria to evaluate the performance of a sensing algorithm.
Stacking the signals from the  antennas/receivers yields the following
antennas/receivers yields the following  vectors:
vectors:

The hypothesis testing problem based on  signal samples is then obtained as
signal samples is then obtained as

3. Neyman-Pearson Theorem
The Neyman-Pearson (NP) theorem [13, 54, 55] states that, for a given probability of false alarm, the test statistic that maximizes the probability of detection is the likelihood ratio test (LRT) defined as

where  denotes the probability density function (PDF), and
denotes the probability density function (PDF), and  denotes the received signal vector that is the aggregation of
denotes the received signal vector that is the aggregation of  Such a likelihood ratio test decides
Such a likelihood ratio test decides  when
when  exceeds a threshold
exceeds a threshold  , and
, and  otherwise.
otherwise.
The major difficulty in using the LRT is its requirements on the exact distributions given in (5). Obviously, the distribution of random vector  under
under  is related to the source signal distribution, the wireless channels, and the noise distribution, while the distribution of
is related to the source signal distribution, the wireless channels, and the noise distribution, while the distribution of  under
under  is related to the noise distribution. In order to use the LRT, we need to obtain the knowledge of the channels as well as the signal and noise distributions, which is practically difficult to realize.
is related to the noise distribution. In order to use the LRT, we need to obtain the knowledge of the channels as well as the signal and noise distributions, which is practically difficult to realize.
If we assume that the channels are flat-fading, and the received source signal sample  's are independent over
's are independent over  , the PDFs in LRT are decoupled as
, the PDFs in LRT are decoupled as

If we further assume that noise and signal samples are both Gaussian distributed, that is,  and
and  , the LRT becomes the estimator-correlator (EC) [13] detector for which the test statistic is given by
, the LRT becomes the estimator-correlator (EC) [13] detector for which the test statistic is given by

From (4), we see that  is actually the minimum-mean-squared-error (MMSE) estimation of the source signal
is actually the minimum-mean-squared-error (MMSE) estimation of the source signal  . Thus,
. Thus,  in (7) can be seen as the correlation of the observed signal
in (7) can be seen as the correlation of the observed signal  with the MMSE estimation of
with the MMSE estimation of  .
.
The EC detector needs to know the source signal covariance matrix  and noise power
and noise power  . When the signal presence is unknown yet, it is unrealistic to require the source signal covariance matrix (related to unknown channels) for detection. Thus, if we further assume that
. When the signal presence is unknown yet, it is unrealistic to require the source signal covariance matrix (related to unknown channels) for detection. Thus, if we further assume that  , the EC detector in (7) reduces to the well-known energy detector (ED) [9, 14] for which the test statistic is given as follows (by discarding irrelevant constant terms):
, the EC detector in (7) reduces to the well-known energy detector (ED) [9, 14] for which the test statistic is given as follows (by discarding irrelevant constant terms):

Note that for the multi-antenna/receiver case,  is actually the summation of signals from all antennas, which is a straightforward cooperative sensing scheme [41, 56, 57]. In general, the ED is not optimal if
is actually the summation of signals from all antennas, which is a straightforward cooperative sensing scheme [41, 56, 57]. In general, the ED is not optimal if  is non-diagonal.
is non-diagonal.
If we assume that noise is Gaussian distributed and source signal  is deterministic and known to the receiver, which is the case for radar signal processing [32, 33, 58], it is easy to show that the LRT in this case becomes the matched filtering-based detector, for which the test statistic is
is deterministic and known to the receiver, which is the case for radar signal processing [32, 33, 58], it is easy to show that the LRT in this case becomes the matched filtering-based detector, for which the test statistic is

4. Bayesian Method and the Generalized Likelihood Ratio Test
In most practical scenarios, it is impossible to know the likelihood functions exactly, because of the existence of uncertainty about one or more parameters in these functions. For instance, we may not know the noise power  and/or source signal covariance
and/or source signal covariance  . Hypothesis testing in the presence of uncertain parameters is known as "composite" hypothesis testing. In classic detection theory, there are two main approaches to tackle this problem: the Bayesian method and the generalized likelihood ratio test (GLRT).
. Hypothesis testing in the presence of uncertain parameters is known as "composite" hypothesis testing. In classic detection theory, there are two main approaches to tackle this problem: the Bayesian method and the generalized likelihood ratio test (GLRT).
In the Bayesian method [13], the objective is to evaluate the likelihood functions needed in the LRT through marginalization, that is,

where  represents all the unknowns when
represents all the unknowns when  is true. Note that the integration operation in (10) should be replaced with a summation if the elements in
is true. Note that the integration operation in (10) should be replaced with a summation if the elements in  are drawn from a discrete sample space. Critically, we have to assign a prior distribution
are drawn from a discrete sample space. Critically, we have to assign a prior distribution  to the unknown parameters. In other words, we need to treat these unknowns as random variables and use their known distributions to express our belief in their values. Similarly,
to the unknown parameters. In other words, we need to treat these unknowns as random variables and use their known distributions to express our belief in their values. Similarly,  can be defined. The main drawbacks of the Bayesian approach are listed as follows.
can be defined. The main drawbacks of the Bayesian approach are listed as follows.
-
(1)
The marginalization operation in (10) is often not tractable except for very simple cases.
-
(2)
The choice of prior distributions affects the detection performance dramatically and thus it is not a trivial task to choose them.
To make the LRT applicable, we may estimate the unknown parameters first and then use the estimated parameters in the LRT. Known estimation techniques could be used for this purpose [59]. However, there is one major difference from the conventional estimation problem where we know that signal is present, while in the case of spectrum sensing we are not sure whether there is source signal or not (the first priority here is the detection of signal presence). At different hypothesis ( or
or  ), the unknown parameters are also different.
), the unknown parameters are also different.
The GLRT is one efficient method [13, 55] to resolve the above problem, which has been used in many applications, for example, radar and sonar signal processing. For this method, the maximum likelihood (ML) estimation of the unknown parameters under  and
and  is first obtained as
is first obtained as

where  and
and  are the set of unknown parameters under
are the set of unknown parameters under  and
and  , respectively. Then, the GLRT statistic is formed as
, respectively. Then, the GLRT statistic is formed as

Finally, the GLRT decides  if
if  , where
, where  is a threshold, and
is a threshold, and  otherwise.
otherwise.
It is not guaranteed that the GLRT is optimal or approaches to be optimal when the sample size goes to infinity. Since the unknown parameters in  and
and  are highly dependent on the noise and signal statistical models, the estimations of them could be vulnerable to the modeling errors. Under the assumption of Gaussian distributed source signals and noises, and flat-fading channels, some efficient spectrum sensing methods based on the GLRT can be found in [60].
are highly dependent on the noise and signal statistical models, the estimations of them could be vulnerable to the modeling errors. Under the assumption of Gaussian distributed source signals and noises, and flat-fading channels, some efficient spectrum sensing methods based on the GLRT can be found in [60].
5. Exploiting Spatial Correlation of Multiple Received Signals
The received signal samples at different antennas/receivers are usually correlated, because all  's are generated from the same source signal
's are generated from the same source signal  's. As mentioned previously, the energy detection defined in (8) is not optimal for this case. Furthermore, it is difficult to realize the LRT in practice. Hence, we consider suboptimal sensing methods as follows.
's. As mentioned previously, the energy detection defined in (8) is not optimal for this case. Furthermore, it is difficult to realize the LRT in practice. Hence, we consider suboptimal sensing methods as follows.
If  , and assuming that the propagation channels are flat-fading (
, and assuming that the propagation channels are flat-fading ( ) and known to the receiver, the energy at different antennas can be coherently combined to obtain a nearly optimal detection [41, 43, 57]. This is also called maximum ratio combining (MRC). However, in practice, the channel coefficients are unknown at the receiver. As a result, the coherent combining may not be applicable and the equal gain combining (EGC) is used in practice [41, 57], which is the same as the energy detection defined in (8).
) and known to the receiver, the energy at different antennas can be coherently combined to obtain a nearly optimal detection [41, 43, 57]. This is also called maximum ratio combining (MRC). However, in practice, the channel coefficients are unknown at the receiver. As a result, the coherent combining may not be applicable and the equal gain combining (EGC) is used in practice [41, 57], which is the same as the energy detection defined in (8).
In general, we can choose a matrix  with
with  rows to combine the signals from all antennas as
rows to combine the signals from all antennas as

The combining matrix should be chosen such that the resultant signal has the largest SNR. It is obvious that the SNR after combining is

where  denotes the mathematical expectation. Hence, the optimal combining matrix should maximize the value of function
denotes the mathematical expectation. Hence, the optimal combining matrix should maximize the value of function  . Let
. Let  be the statistical covariance matrix of the primary signals. It can be verified that
be the statistical covariance matrix of the primary signals. It can be verified that

where  denotes the trace of a matrix. Let
denotes the trace of a matrix. Let  be the maximum eigenvalue of
be the maximum eigenvalue of  and let
and let  be the corresponding eigenvector. It can be proved that the optimal combining matrix degrades to the vector
be the corresponding eigenvector. It can be proved that the optimal combining matrix degrades to the vector  [29].
[29].
Upon substituting  into (13), the test statistic for the energy detection becomes
into (13), the test statistic for the energy detection becomes

The resulting detection method is called optimally combined energy detection (OCED) [29]. It is easy to show that this test statistic is better than  in terms of SNR.
in terms of SNR.
The OCED needs an eigenvector of the received source signal covariance matrix, which is usually unknown. To overcome this difficulty, we provide a method to estimate the eigenvector using the received signal samples only. Considering the statistical covariance matrix of the signal defined as

we can verify that

Since  and
and  have the same eigenvectors, the vector
have the same eigenvectors, the vector  is also the eigenvector of
is also the eigenvector of  corresponding to its maximum eigenvalue. However, in practice, we do not know the statistical covariance matrix
corresponding to its maximum eigenvalue. However, in practice, we do not know the statistical covariance matrix  either, and therefore we cannot obtain the exact vector
either, and therefore we cannot obtain the exact vector  . An approximation of the statistical covariance matrix is the sample covariance matrix defined as
. An approximation of the statistical covariance matrix is the sample covariance matrix defined as

Let  (normalized to
(normalized to  ) be the eigenvector of the sample covariance matrix corresponding to its maximum eigenvalue. We can replace the combining vector
) be the eigenvector of the sample covariance matrix corresponding to its maximum eigenvalue. We can replace the combining vector  by
by  , that is,
, that is,

Then, the test statistics for the resulting blindly combined energy detection (BCED) [29] becomes

It can be verified that

where  is the maximum eigenvalue of
is the maximum eigenvalue of  . Thus,
. Thus,  can be taken as the maximum eigenvalue of the sample covariance matrix. Note that this test is a special case of the eigenvalue-based detection (EBD) [20–25].
can be taken as the maximum eigenvalue of the sample covariance matrix. Note that this test is a special case of the eigenvalue-based detection (EBD) [20–25].
6. Combining Space and Time Correlation
In addition to being spatially correlated, the received signal samples are usually correlated in time due to the following reasons.
 The received signal is oversampled. Let
The received signal is oversampled. Let  be the Nyquist sampling period of continuous-time signal
be the Nyquist sampling period of continuous-time signal  and let
and let  be the sampled signal based on the Nyquist sampling rate. Thanks to the Nyquist theorem, the signal
be the sampled signal based on the Nyquist sampling rate. Thanks to the Nyquist theorem, the signal  can be expressed as
can be expressed as

where  is an interpolation function. Hence, the signal samples
is an interpolation function. Hence, the signal samples  are only related to
are only related to  , where
, where  is the actual sampling period. If the sampling rate at the receiver is
is the actual sampling period. If the sampling rate at the receiver is  , that is,
, that is,  , then
, then  must be correlated over
must be correlated over  . An example of this is the wireless microphone signal specified in the IEEE 802.22 standard [6, 7], which occupies about 200 KHz in a 6-MHz TV band. In this example, if we sample the received signal with sampling rate no lower than 6 MHz, the wireless microphone signal is actually oversampled and the resulting signal samples are highly correlated in time.
. An example of this is the wireless microphone signal specified in the IEEE 802.22 standard [6, 7], which occupies about 200 KHz in a 6-MHz TV band. In this example, if we sample the received signal with sampling rate no lower than 6 MHz, the wireless microphone signal is actually oversampled and the resulting signal samples are highly correlated in time.
 The propagation channel is time-dispersive. In this case, the received signal can be expressed as
The propagation channel is time-dispersive. In this case, the received signal can be expressed as

where  is the transmitted signal and
is the transmitted signal and  is the response of the time-dispersive channel. Since the sampling period
is the response of the time-dispersive channel. Since the sampling period  is usually very small, the integration (24) can be approximated as
is usually very small, the integration (24) can be approximated as

Hence,

where  is the support of the channel response
is the support of the channel response  , with
, with  for
for  . For time-dispersive channels,
. For time-dispersive channels,  and thus even if the original signal samples
and thus even if the original signal samples  's are i.i.d., the received signal samples
's are i.i.d., the received signal samples  's are correlated.
's are correlated.
 The transmitted signal is correlated in time. In this case, even if the channel is flat-fading and there is no oversampling at the receiver, the received signal samples are correlated.
The transmitted signal is correlated in time. In this case, even if the channel is flat-fading and there is no oversampling at the receiver, the received signal samples are correlated.
The above discussions suggest that the assumption of independent (in time) received signal samples may be invalid in practice, such that the detection methods relying on this assumption may not perform optimally. However, additional correlation in time may not be harmful for signal detection, while the problem is how we can exploit this property. For the multi-antenna/receiver case, the received signal samples are also correlated in space. Thus, to use both the space and time correlations, we may stack the signals from the  antennas and over
antennas and over  sampling periods all together and define the corresponding
sampling periods all together and define the corresponding  signal/noise vectors:
signal/noise vectors:



Then, by replacing  by
by  , we can directly extend the previously introduced OCED and BCED methods to incorporate joint space-time processing. Similarly, the eigenvalue-based detection methods [21–24] can also be modified to work for correlated signals in both time and space. Another approach to make use of space-time signal correlation is the covariance based detection [27, 28, 61] briefly described as follows. Defining the space-time statistical covariance matrices for the signal and noise as
, we can directly extend the previously introduced OCED and BCED methods to incorporate joint space-time processing. Similarly, the eigenvalue-based detection methods [21–24] can also be modified to work for correlated signals in both time and space. Another approach to make use of space-time signal correlation is the covariance based detection [27, 28, 61] briefly described as follows. Defining the space-time statistical covariance matrices for the signal and noise as

respectively, we can verify that

If the signal is not present,  , and thus the off-diagonal elements in
, and thus the off-diagonal elements in  are all zeros. If there is a signal and the signal samples are correlated,
are all zeros. If there is a signal and the signal samples are correlated,  is not a diagonal matrix. Hence, the nonzero off-diagonal elements of
is not a diagonal matrix. Hence, the nonzero off-diagonal elements of  can be used for signal detection.
can be used for signal detection.
In practice, the statistical covariance matrix can only be computed using a limited number of signal samples, where  can be approximated by the sample covariance matrix defined as
can be approximated by the sample covariance matrix defined as

Based on the sample covariance matrix, we could develop the covariance absolute value (CAV) test [27, 28] defined as

where  denotes the
denotes the  th element of the sample covariance matrix
th element of the sample covariance matrix  .
.
There are other ways to utilize the elements in the sample covariance matrix, for example, the maximum value of the nondiagonal elements, to form different test statistics. Especially, when we have some prior information on the source signal correlation, we may choose a corresponding subset of the elements in the sample covariance matrix to form a more efficient test.
Another effective usage of the covariance matrix for sensing is the eigenvalue based detection (EBD) [20–25], which uses the eigenvalues of the covariance matrix as test statistics.
7. Cyclostationary Detection
Practical communication signals may have special statistical features. For example, digital modulated signals have nonrandom components such as double sidedness due to sinewave carrier and keying rate due to symbol period. Such signals have a special statistical feature called cyclostationarity, that is, their statistical parameters vary periodically in time. This cyclostationarity can be extracted by the spectral-correlation density (SCD) function [16–18]. For a cyclostationary signal, its SCD function takes nonzero values at some nonzero cyclic frequencies. On the other hand, noise does not have any cyclostationarity at all; that is, its SCD function has zero values at all non-zero cyclic frequencies. Hence, we can distinguish signal from noise by analyzing the SCD function. Furthermore, it is possible to distinguish the signal type because different signals may have different non-zero cyclic frequencies.
In the following, we list cyclic frequencies for some signals of practical interest [17, 18].
-
(1)
Analog TV signal: it has cyclic frequencies at multiples of the TV-signal horizontal line-scan rate (15.75?KHz in USA, 15.625 KHz in Europe).
-
(2)
AM signal:
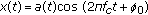 . It has cyclic frequencies at
. It has cyclic frequencies at 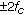 .
. -
(3)
PM and FM signal:
 . It usually has cyclic frequencies at
. It usually has cyclic frequencies at 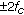 . The characteristics of the SCD function at cyclic frequency
. The characteristics of the SCD function at cyclic frequency 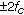 depend on
depend on 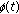 .
. -
(4)
Digital-modulated signals are as follows
-
(a)
Amplitude-Shift Keying:
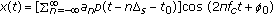 . It has cyclic frequencies at
. It has cyclic frequencies at 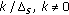 and
and 
-
(b)
Phase-Shift Keying:
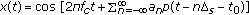 . For BPSK, it has cyclic frequencies at
. For BPSK, it has cyclic frequencies at 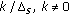 , and
, and 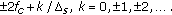 For QPSK, it has cycle frequencies at
For QPSK, it has cycle frequencies at  .
.
-
(a)
When source signal  passes through a wireless channel, the received signal is impaired by the unknown propagation channel. In general, the received signal can be written as
passes through a wireless channel, the received signal is impaired by the unknown propagation channel. In general, the received signal can be written as

where  denotes the convolution, and
denotes the convolution, and  denotes the channel response. It can be shown that the SCD function of
denotes the channel response. It can be shown that the SCD function of  is
is

where  denotes the conjugate,
denotes the conjugate,  denotes the cyclic frequency for
denotes the cyclic frequency for  ,
,  is the Fourier transform of the channel
is the Fourier transform of the channel  , and
, and  is the SCD function of
is the SCD function of  . Thus, the unknown channel could have major impacts on the strength of SCD at certain cyclic frequencies.
. Thus, the unknown channel could have major impacts on the strength of SCD at certain cyclic frequencies.
Although cyclostationary detection has certain advantages (e.g., robustness to uncertainty in noise power and propagation channel), it also has some disadvantages:  it needs a very high sampling rate;
it needs a very high sampling rate;  the computation of SCD function requires large number of samples and thus high computational complexity;
the computation of SCD function requires large number of samples and thus high computational complexity;  the strength of SCD could be affected by the unknown channel;
the strength of SCD could be affected by the unknown channel;  the sampling time error and frequency offset could affect the cyclic frequencies.
the sampling time error and frequency offset could affect the cyclic frequencies.
8. Cooperative Sensing
When there are multiple users/receivers distributed in different locations, it is possible for them to cooperate to achieve higher sensing reliability, thus resulting in various cooperative sensing schemes [34–44, 53, 62]. Generally speaking, if each user sends its observed data or processed data to a specific user, which jointly processes the collected data and makes a final decision, this cooperative sensing scheme is called data fusion. Alternatively, if multiple receivers process their observed data independently and send their decisions to a specific user, which then makes a final decision, it is called decision fusion.
8.1. Data Fusion
If the raw data from all receivers are sent to a central processor, the previously discussed methods for multi-antenna sensing can be directly applied. However, communication of raw data may be very expensive for practical applications. Hence, in many cases, users only send processed/compressed data to the central processor.
A simple cooperative sensing scheme based on the energy detection is the combined energy detection. For this scheme, each user computes its received source signal (including the noise) energy as  and sends it to the central processor, which sums the collected energy values using a linear combination (LC) to obtain the following test statistic:
and sends it to the central processor, which sums the collected energy values using a linear combination (LC) to obtain the following test statistic:

where  is the combining coefficient, with
is the combining coefficient, with  and
and  . If there is no information on the source signal power received by each user, the EGC can be used, that is,
. If there is no information on the source signal power received by each user, the EGC can be used, that is,  for all
for all  . If the source signal power received by each user is known, the optimal combining coefficients can be found [38, 43]. For the low-SNR case, it can be shown [43] that the optimal combining coefficients are given by
. If the source signal power received by each user is known, the optimal combining coefficients can be found [38, 43]. For the low-SNR case, it can be shown [43] that the optimal combining coefficients are given by

where  is the received source signal (excluding the noise) power of user
is the received source signal (excluding the noise) power of user  .
.
A fusion scheme based on the CAV is given in [53], which has the capability to mitigate interference and noise uncertainty.
8.2. Decision Fusion
In decision fusion, each user sends its one-bit or multiple-bit decision to a central processor, which deploys a fusion rule to make the final decision. Specifically, if each user only sends one-bit decision ("1" for signal present and "0" for signal absent) and no other information is available at the central processor, some commonly adopted decision fusion rules are described as follows [42].
-
(1)
"Logical-OR (LO)" Rule: If one of the decisions is "1," the final decision is "1." Assuming that all decisions are independent, then the probability of detection and probability of false alarm of the final decision are
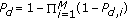 and
and  , respectively, where
, respectively, where 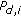 and
and  are the probability of detection and probability of false alarm for user
are the probability of detection and probability of false alarm for user  , respectively.
, respectively. -
(2)
"Logical-AND (LA)" Rule: If and only if all decisions are "1," the final decision is "1." The probability of detection and probability of false alarm of the final decision are
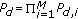 and
and 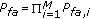 , respectively.
, respectively. -
(3)
"
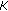 out of
out of  " Rule: If and only if
" Rule: If and only if 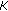 decisions or more are "1"s, the final decision is "1." This includes "Logical-OR (LO)" (
decisions or more are "1"s, the final decision is "1." This includes "Logical-OR (LO)" ( ), "Logical-AND (LA)" (
), "Logical-AND (LA)" (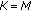 ), and "Majority" (
), and "Majority" ( ) as special cases [34]. The probability of detection and probability of false alarm of the final decision are
) as special cases [34]. The probability of detection and probability of false alarm of the final decision are (38)
(38)respectively.
Alternatively, each user can send multiple-bit decision such that the central processor gets more information to make a more reliable decision. A fusion scheme based on multiple-bit decisions is shown in [41]. In general, there is a tradeoff between the number of decision bits and the fusion reliability. There are also other fusion rules that may require additional information [34, 63].
Although cooperative sensing can achieve better performance, there are some issues associated with it. First, reliable information exchanges among the cooperating users must be guaranteed. In an ad hoc network, this is by no means a simple task. Second, most data fusion methods in literature are based on the simple energy detection and flat-fading channel model, while more advanced data fusion algorithms such as cyclostationary detection, space-time combining, and eigenvalue-based detection, over more practical propagation channels need to be further investigated. Third, existing decision fusions have mostly assumed that decisions of different users are independent, which may not be true because all users actually receive signals from some common sources. At last, practical fusion algorithms should be robust to data errors due to channel impairment, interference, and noise.
9. Noise Power Uncertainty and Estimation
For many detection methods, the receiver noise power is assumed to be known a priori, in order to form the test statistic and/or set the test threshold. However, the noise power level may change over time, thus yielding the so-called noise uncertainty problem. There are two types of noise uncertainty: receiver device noise uncertainty and environment noise uncertainty. The receiver device noise uncertainty comes from [9–11]: (a) nonlinearity of receiver components and (b) time-varying thermal noise in these components. The environment noise uncertainty is caused by transmissions of other users, either unintentionally or intentionally. Because of the noise uncertainty, in practice, it is very difficult to obtain the accurate noise power.
Let the estimated noise power be  , where
, where  is called the noise uncertainty factor. The upper bound on
is called the noise uncertainty factor. The upper bound on  (in dB scale) is then defined as
(in dB scale) is then defined as

where  is called the noise uncertainty bound. It is usually assumed that
is called the noise uncertainty bound. It is usually assumed that  in dB scale, that is,
in dB scale, that is,  , is uniformly distributed in the interval
, is uniformly distributed in the interval  [10]. In practice, the noise uncertainty bound of a receiving device is normally below 2 dB [10, 64], while the environment/interference noise uncertainty can be much larger [10]. When there is noise uncertainty, it is known that the energy detection is not effective [9–11, 64].
[10]. In practice, the noise uncertainty bound of a receiving device is normally below 2 dB [10, 64], while the environment/interference noise uncertainty can be much larger [10]. When there is noise uncertainty, it is known that the energy detection is not effective [9–11, 64].
To resolve the noise uncertainty problem, we need to estimate the noise power in real time. For the multi-antenna case, if we know that the number of active primary signals,  , is smaller than
, is smaller than  , the minimum eigenvalue of the sample covariance matrix can be a reasonable estimate of the noise power. If we further assume to know the difference
, the minimum eigenvalue of the sample covariance matrix can be a reasonable estimate of the noise power. If we further assume to know the difference  , the average of the
, the average of the  smallest eigenvalues can be used as a better estimate of the noise power. Accordingly, instead of comparing the test statistics with an assumed noise power, we can compare them with the estimated noise power from the sample covariance matrix. For example, we can compare
smallest eigenvalues can be used as a better estimate of the noise power. Accordingly, instead of comparing the test statistics with an assumed noise power, we can compare them with the estimated noise power from the sample covariance matrix. For example, we can compare  and
and  with the minimum eigenvalue of the sample covariance matrix, resulting in the maximum to minimum eigenvalue (MME) detection and energy to minimum eigenvalue (EME) detection, respectively [21, 22]. These methods can also be used for the single-antenna case if signal samples are time-correlated [22].
with the minimum eigenvalue of the sample covariance matrix, resulting in the maximum to minimum eigenvalue (MME) detection and energy to minimum eigenvalue (EME) detection, respectively [21, 22]. These methods can also be used for the single-antenna case if signal samples are time-correlated [22].
Figures 1 and 2 show the Receiver Operating Characteristics (ROC) curves ( versus
versus  ) at
) at  dB,
dB,  ,
,  , and
, and  . In Figure 1, the source signal is i.i.d and the flat-fading channel is assumed, while in Figure 2, the source signal is the wireless microphone signal [61, 65] and the multipath fading channel (with eight independent taps of equal power) is assumed. For Figure 2, in order to exploit the correlation of signal samples in both space and time, the received signal samples are stacked as in (27). In both figures, "ED-x dB" means the energy detection with x-dB noise uncertainty. Note that both BCED and ED use the true noise power to set the test threshold, while MME and EME only use the estimated noise power as the minimum eigenvalue of the sample covariance matrix. It is observed that for both cases of i.i.d source (Figure 1) and correlated source (Figure 2), BCED performs better than ED, and so does MME than EME. Comparing Figures 1 and 2, we see that BCED and MME work better for correlated source signals, while the reverse is true for ED and EME. It is also observed that the performance of ED degrades dramatically when there is noise power uncertainty.
. In Figure 1, the source signal is i.i.d and the flat-fading channel is assumed, while in Figure 2, the source signal is the wireless microphone signal [61, 65] and the multipath fading channel (with eight independent taps of equal power) is assumed. For Figure 2, in order to exploit the correlation of signal samples in both space and time, the received signal samples are stacked as in (27). In both figures, "ED-x dB" means the energy detection with x-dB noise uncertainty. Note that both BCED and ED use the true noise power to set the test threshold, while MME and EME only use the estimated noise power as the minimum eigenvalue of the sample covariance matrix. It is observed that for both cases of i.i.d source (Figure 1) and correlated source (Figure 2), BCED performs better than ED, and so does MME than EME. Comparing Figures 1 and 2, we see that BCED and MME work better for correlated source signals, while the reverse is true for ED and EME. It is also observed that the performance of ED degrades dramatically when there is noise power uncertainty.
10. Detection Threshold and Test Statistic Distribution
To make a decision on whether signal is present, we need to set a threshold  for each proposed test statistic, such that certain
for each proposed test statistic, such that certain  and/or
and/or  can be achieved. For a fixed sample size
can be achieved. For a fixed sample size  , we cannot set the threshold to meet the targets for arbitrarily high
, we cannot set the threshold to meet the targets for arbitrarily high  and low
and low  at the same time, as they are conflicting to each other. Since we have little or no prior information on the signal (actually we even do not know whether there is a signal or not), it is difficult to set the threshold based on
at the same time, as they are conflicting to each other. Since we have little or no prior information on the signal (actually we even do not know whether there is a signal or not), it is difficult to set the threshold based on  . Hence, a common practice is to choose the threshold based on
. Hence, a common practice is to choose the threshold based on  under hypothesis
under hypothesis  .
.
Without loss of generality, the test threshold can be decomposed into the following form:  , where
, where  is related to the sample size
is related to the sample size  and the target
and the target  , and
, and  is a statistic related to the noise distribution under
is a statistic related to the noise distribution under  . For example, for the energy detection with known noise power, we have
. For example, for the energy detection with known noise power, we have

For the matched-filtering detection with known noise power, we have

For the EME/MME detection with no knowledge on the noise power, we have

where  is the minimum eigenvalue of the sample covariance matrix. For the CAV detection, we can set
is the minimum eigenvalue of the sample covariance matrix. For the CAV detection, we can set

In practice, the parameter  can be set either empirically based on the observations over a period of time when the signal is known to be absent, or analytically based on the distribution of the test statistic under
can be set either empirically based on the observations over a period of time when the signal is known to be absent, or analytically based on the distribution of the test statistic under  . In general, such distributions are difficult to find, while some known results are given as follows.
. In general, such distributions are difficult to find, while some known results are given as follows.
For energy detection defined in (8), it can be shown that for a sufficiently large values of  , its test statistic can be well approximated by the Gaussian distribution, that is,
, its test statistic can be well approximated by the Gaussian distribution, that is,

Accordingly, for given  and
and  , the corresponding
, the corresponding  can be found as
can be found as

where

For the matched-filtering detection defined in (9), for a sufficiently large  , we have
, we have

Thereby, for given  and
and  , it can be shown that
, it can be shown that

For the GLRT-based detection, it can be shown that the asymptotic (as  ) log-likelihood ratio is central chi-square distributed [13]. More precisely,
) log-likelihood ratio is central chi-square distributed [13]. More precisely,

where  is the number of independent scalar unknowns under
is the number of independent scalar unknowns under  and
and  . For instance, if
. For instance, if  is known while
is known while  is not,
is not,  will be equal to the number of independent real-valued scalar variables in
will be equal to the number of independent real-valued scalar variables in  . However, there is no explicit expression for
. However, there is no explicit expression for  in this case.
in this case.
Random matrix theory (RMT) is useful for determining the test statistic distribution and the parameter  for the class of eigenvalue-based detection methods. In the following, we provide an example for the BCED detection method with known noise power, that is,
for the class of eigenvalue-based detection methods. In the following, we provide an example for the BCED detection method with known noise power, that is,  . For this method, we actually compare the ratio of the maximum eigenvalue of the sample covariance matrix
. For this method, we actually compare the ratio of the maximum eigenvalue of the sample covariance matrix  to the noise power
to the noise power  with a threshold
with a threshold  . To set the value for
. To set the value for  , we need to know the distribution of
, we need to know the distribution of  for any finite
for any finite  . With a finite
. With a finite  ,
,  may be very different from the actual covariance matrix
may be very different from the actual covariance matrix  due to the noise. In fact, characterizing the eigenvalue distributions for
due to the noise. In fact, characterizing the eigenvalue distributions for  is a very complicated problem [66–69], which also makes the choice of
is a very complicated problem [66–69], which also makes the choice of  difficult in general.
difficult in general.
When there is no signal,  reduces to
reduces to  , which is the sample covariance matrix of the noise only. It is known that
, which is the sample covariance matrix of the noise only. It is known that  is a Wishart random matrix [66]. The study of the eigenvalue distributions for random matrices is a very hot research topic over recent years in mathematics, communications engineering, and physics. The joint PDF of the ordered eigenvalues of a Wishart random matrix has been known for many years [66]. However, since the expression of the joint PDF is very complicated, no simple closed-form expressions have been found for the marginal PDFs of the ordered eigenvalues, although some computable expressions have been found in [70]. Recently, Johnstone and Johansson have found the distribution of the largest eigenvalue [67, 68] of a Wishart random matrix as described in the following theorem.
is a Wishart random matrix [66]. The study of the eigenvalue distributions for random matrices is a very hot research topic over recent years in mathematics, communications engineering, and physics. The joint PDF of the ordered eigenvalues of a Wishart random matrix has been known for many years [66]. However, since the expression of the joint PDF is very complicated, no simple closed-form expressions have been found for the marginal PDFs of the ordered eigenvalues, although some computable expressions have been found in [70]. Recently, Johnstone and Johansson have found the distribution of the largest eigenvalue [67, 68] of a Wishart random matrix as described in the following theorem.
Theorem 1.
Let  ,
,  , and
, and  . Assume that
. Assume that  . Then,
. Then,  converges (with probability one) to the Tracy-Widom distribution of order 1 [71, 72].
converges (with probability one) to the Tracy-Widom distribution of order 1 [71, 72].
The Tracy-Widom distribution provides the limiting law for the largest eigenvalue of certain random matrices [71, 72]. Let  be the cumulative distribution function (CDF) of the Tracy-Widom distribution of order 1. We have
be the cumulative distribution function (CDF) of the Tracy-Widom distribution of order 1. We have

where  is the solution of the nonlinear Painlevé II differential equation given by
is the solution of the nonlinear Painlevé II differential equation given by

Accordingly, numerical solutions can be found for function  at different values of
at different values of  . Also, there have been tables for values of
. Also, there have been tables for values of  [67] and Matlab codes to compute them [73].
[67] and Matlab codes to compute them [73].
Based on the above results, the probability of false alarm for the BCED detection can be obtained as

which leads to

or equivalently,

From the definitions of  and
and  in Theorem 1, we finally obtain the value for
in Theorem 1, we finally obtain the value for  as
as

Note that  depends only on
depends only on  and
and  . A similar approach like the above can be used for the case of MME detection, as shown in [21, 22].
. A similar approach like the above can be used for the case of MME detection, as shown in [21, 22].
Figure 3 shows the expected (theoretical) and actual (by simulation) probability of false alarm values based on the theoretical threshold in (55) for  , and
, and  . It is observed that the differences between these two sets of values are reasonably small, suggesting that the choice of the theoretical threshold is quite accurate.
. It is observed that the differences between these two sets of values are reasonably small, suggesting that the choice of the theoretical threshold is quite accurate.
11. Robust Spectrum Sensing
In many detection applications, the knowledge of signal and/or noise is limited, incomplete, or imprecise. This is especially true in cognitive radio systems, where the primary users usually do not cooperate with the secondary users and as a result the wireless propagation channels between the primary and secondary users are hard to be predicted or estimated. Moreover, intentional or unintentional interference is very common in wireless communications such that the resulting noise distribution becomes unpredictable. Suppose that a detector is designed for specific signal and noise distributions. A pertinent question is then as follows: how sensitive is the performance of the detector to the errors in signal and/or noise distributions? In many situations, the designed detector based on the nominal assumptions may suffer a drastic degradation in performance even with small deviations from the assumptions. Consequently, the searching for robust detection methods has been of great interest in the field of signal processing and many others [74–77]. A very useful paradigm to design robust detectors is the maxmin approach, which maximizes the worst case detection performance. Among others, two techniques are very useful for robust cognitive radio spectrum sensing: the robust hypothesis testing [75] and the robust matched filtering [76, 77]. In the following, we will give a brief overview on them, while for other robust detection techniques, the interested readers may refer to the excellent survey paper [78] and references therein.
11.1. Robust Hypothesis Testing
Let the PDF of a received signal sample be  at hypothesis
at hypothesis  and
and  at hypothesis
at hypothesis  . If we know these two functions, the LRT-based detection described in Section 2 is optimal. However, in practice, due to channel impairment, noise uncertainty, and interference, it is very hard, if possible, to obtain these two functions exactly. One possible situation is when we only know that
. If we know these two functions, the LRT-based detection described in Section 2 is optimal. However, in practice, due to channel impairment, noise uncertainty, and interference, it is very hard, if possible, to obtain these two functions exactly. One possible situation is when we only know that  and
and  belong to certain classes. One such class is called the
belong to certain classes. One such class is called the  -contamination class given by
-contamination class given by

where  (
( ) is the nominal PDF under hypothesis
) is the nominal PDF under hypothesis  ,
,  in
in  is the maximum degree of contamination, and
is the maximum degree of contamination, and  is an arbitrary density function. Assume that we only know
is an arbitrary density function. Assume that we only know  and
and  (an upper bound for contamination),
(an upper bound for contamination),  . The problem is then to design a detection scheme to minimize the worst-case probability of error (e.g., probability of false alarm plus probability of mis-detection), that is, finding a detector
. The problem is then to design a detection scheme to minimize the worst-case probability of error (e.g., probability of false alarm plus probability of mis-detection), that is, finding a detector  such that
such that

Hubber [75] proved that the optimal test statistic is a "censored" version of the LRT given by

where

and  ,
,  are nonnegative numbers related to
are nonnegative numbers related to  ,
,  ,
,  , and
, and  [75, 78]. Note that if choosing
[75, 78]. Note that if choosing  and
and  , the test is the conventional LRT with respect to nominal PDFs,
, the test is the conventional LRT with respect to nominal PDFs,  and
and  .
.
After this seminal work, there have been quite a few researches in this area [78]. For example, similar minmax solutions are found for some other uncertainty models [78].
11.2. Robust Matched Filtering
We turn the model (4) into a vector form as

where  is the signal vector and
is the signal vector and  is the noise vector. Suppose that
is the noise vector. Suppose that  is known. In general, a matched-filtering detection is
is known. In general, a matched-filtering detection is  . Let the covariance matrix of the noise be
. Let the covariance matrix of the noise be  . If
. If  , it is known that choosing
, it is known that choosing  is optimal. In general, it is easy to verify that the optimal
is optimal. In general, it is easy to verify that the optimal  to maximize the SNR is
to maximize the SNR is

In practice, the signal vector  may not be known exactly. For example,
may not be known exactly. For example,  may be only known to be around
may be only known to be around  with some errors modeled by
with some errors modeled by

where  is an upper bound on the Euclidean-norm of the error. In this case, we are interested in finding a proper value for
is an upper bound on the Euclidean-norm of the error. In this case, we are interested in finding a proper value for  such that the worst-case SNR is maximized, that is,
such that the worst-case SNR is maximized, that is,

It was proved in [76, 77] that the optimal solution for the above maxmin problem is

where  is a nonnegative number such that
is a nonnegative number such that  .
.
It is noted that there are also researches on the robust matched filtering detection when the signal has other types of uncertainty [78]. Moreover, if the noise has uncertainties, that is,  is not known exactly, or both noise and signal have uncertainties, the optimal robust matched-filtering detector was also found for some specific uncertainty models in [78].
is not known exactly, or both noise and signal have uncertainties, the optimal robust matched-filtering detector was also found for some specific uncertainty models in [78].
12. Practical Considerations and Future Developments
Although there have been quite a few methods proposed for spectrum sensing, their realization and performance in practical cognitive radio applications need to be tested [50–52]. To build a practical sensing device, many factors should be considered. Some of them are discussed as follows.
( ) Narrowband noise. One or more narrowband filters may be used to extract the signal from a specific band. These filters can be analog or digital. Only if the filter is ideally designed and the signal is critically sampled (sampling rate is the same as the bandwidth of the filter), the discrete noise samples could be i.i.d. In a practical device, however, the noise samples are usually correlated. This will cause many sensing methods unworkable, because they usually assume that the noise samples are i.i.d. For some methods, a noise prewhitening process can be used to make the noise samples i.i.d. prior to the signal detection. For example, this method has been deployed in [22] to enable the eigenvalue-based detection methods. The similar method can be used for covariance-based detection methods, for example, the CAV.
) Narrowband noise. One or more narrowband filters may be used to extract the signal from a specific band. These filters can be analog or digital. Only if the filter is ideally designed and the signal is critically sampled (sampling rate is the same as the bandwidth of the filter), the discrete noise samples could be i.i.d. In a practical device, however, the noise samples are usually correlated. This will cause many sensing methods unworkable, because they usually assume that the noise samples are i.i.d. For some methods, a noise prewhitening process can be used to make the noise samples i.i.d. prior to the signal detection. For example, this method has been deployed in [22] to enable the eigenvalue-based detection methods. The similar method can be used for covariance-based detection methods, for example, the CAV.
( ) Spurious signal and interference. The received signal may contain not only the desired signal and white noise but also some spurious signal and interference. The spurious signal may be generated by Analog-to-Digital Converters (ADC) due to its nonlinearity [79] or other intentional/unintentional transmitters. If the sensing antenna is near some electronic devices, the spurious signal generated by the devices can be strong in the received signal. For some sensing methods, such unwanted signals will be detected as signals rather than noise. This will increase the probability of false alarm. There are methods to mitigate the spurious signal at the device level [79]. Alternatively, signal processing techniques can be used to eliminate the impact of spurious signal/interference [53]. It is very difficult, if possible, to estimate the interference waveform or distribution because of its variation with time and location. Depending on situations, the interference power could be lower or higher than the noise power. If the interference power is much higher than the noise power, it is possible to estimate the interference first and subtract it from the received signal. However, since we usually intend to detect signal at very low SNR, the error of the interference estimation could be large enough (say, larger than the primary signal) such that the detection with the residue signal after the interference subtraction is still unreliable. If the interference power is low, it is hard to estimate it anyway. Hence, in general we cannot rely on the interference estimation and subtraction, especially for very low-power signal detection.
) Spurious signal and interference. The received signal may contain not only the desired signal and white noise but also some spurious signal and interference. The spurious signal may be generated by Analog-to-Digital Converters (ADC) due to its nonlinearity [79] or other intentional/unintentional transmitters. If the sensing antenna is near some electronic devices, the spurious signal generated by the devices can be strong in the received signal. For some sensing methods, such unwanted signals will be detected as signals rather than noise. This will increase the probability of false alarm. There are methods to mitigate the spurious signal at the device level [79]. Alternatively, signal processing techniques can be used to eliminate the impact of spurious signal/interference [53]. It is very difficult, if possible, to estimate the interference waveform or distribution because of its variation with time and location. Depending on situations, the interference power could be lower or higher than the noise power. If the interference power is much higher than the noise power, it is possible to estimate the interference first and subtract it from the received signal. However, since we usually intend to detect signal at very low SNR, the error of the interference estimation could be large enough (say, larger than the primary signal) such that the detection with the residue signal after the interference subtraction is still unreliable. If the interference power is low, it is hard to estimate it anyway. Hence, in general we cannot rely on the interference estimation and subtraction, especially for very low-power signal detection.
( ) Fixed point realization. Many hardware realizations use fixed point rather than floating point computation. This will limit the accuracy of detection methods due to the signal truncation when it is saturated. A detection method should be robust to such unpredictable errors.
) Fixed point realization. Many hardware realizations use fixed point rather than floating point computation. This will limit the accuracy of detection methods due to the signal truncation when it is saturated. A detection method should be robust to such unpredictable errors.
( ) Wideband sensing. A cognitive radio device may need to monitor a very large contiguous or noncontiguous frequency range to find the best available band(s) for transmission. The aggregate bandwidth could be as large as several GHz. Such wideband sensing requires ultra-wide band RF frontend and very fast signal processing devices. To sense a very large frequency range, typically a corresponding large sampling rate is required, which is very challenging for practical implementation. Fortunately, if a large part of the frequency range is vacant, that is, the signal is frequency-domain sparse, we can use the recently developed compressed sampling (also called compressed sensing) to reduce the sampling rate by a large margin [80–82]. Although there have been studies in wideband sensing algorithms [26, 83–87], more researches are needed especially when the center frequencies and bandwidths of the primary signals are unknown within the frequency range of interest.
) Wideband sensing. A cognitive radio device may need to monitor a very large contiguous or noncontiguous frequency range to find the best available band(s) for transmission. The aggregate bandwidth could be as large as several GHz. Such wideband sensing requires ultra-wide band RF frontend and very fast signal processing devices. To sense a very large frequency range, typically a corresponding large sampling rate is required, which is very challenging for practical implementation. Fortunately, if a large part of the frequency range is vacant, that is, the signal is frequency-domain sparse, we can use the recently developed compressed sampling (also called compressed sensing) to reduce the sampling rate by a large margin [80–82]. Although there have been studies in wideband sensing algorithms [26, 83–87], more researches are needed especially when the center frequencies and bandwidths of the primary signals are unknown within the frequency range of interest.
( ) Complexity. This is of course one of the major factors affecting the implementation of a sensing method. Simple but effective methods are always preferable.
) Complexity. This is of course one of the major factors affecting the implementation of a sensing method. Simple but effective methods are always preferable.
To detect a desired signal at very low SNR and in a harsh environment is by no means a simple task. In this paper, major attention is paid to the statistical detection methods. The major advantage of such methods is their little dependency on signal/channel knowledge as well as relative ease for realization. However, their disadvantage is also obvious: they are in general vulnerable to undesired interferences. How we can effectively combine the statistical detection with known signal features is not yet well understood. This might be a promising research direction. Furthermore, most exiting spectrum sensing methods are passive in the sense that they have neglected the interactions between the primary and secondary networks via their mutual interferences. If the reaction of the primary user (e.g., power control) upon receiving the secondary interference is exploited, some active spectrum sensing methods can be designed, which could significantly outperform the conventional passive sensing methods [88, 89]. At last, detecting the presence of signal is only the basic task of sensing. For a radio with high level of cognition, further information such as signal waveform and modulation schemes may be exploited. Therefore, signal identification turns to be an advanced task of sensing. If we could find an effective method for this advanced task, it in turn can help the basic sensing task.
13. Conclusion
In this paper, various spectrum sensing techniques have been reviewed. Special attention has been paid to blind sensing methods that do not need information of the source signals and the propagation channels. It has been shown that space-time joint signal processing not only improves the sensing performance but also solves the noise uncertainty problem to some extent. Theoretical analysis on test statistic distribution and threshold setting has also been investigated.
References
FCC : Spectrum policy task force report. Proceedings of the Federal Communications Commission (FCC '02), November 2002, Washington, DC, USA
Islam MH, Koh CL, Oh SW, et al.: Spectrum survey in Singapore: occupancy measurements and analysis. Proceedings of the 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM '08), May 2008, Singapor
Mitola J, Maguire GQ: Cognitive radio: making software radios more personal. IEEE Personal Communications 1999, 6(4):13-18. 10.1109/98.788210
Haykin S: Cognitive radio: brain-empowered wireless communications. IEEE Transactions on Communications 2005, 23(2):201-220.
Devroye N, Mitran P, Tarokh V: Achieveable rates in cognitive radio channels. IEEE Transactions on Information Theory 2006, 52(5):1813-1827.
802.22 Working Group : IEEE 802.22 D1: draft standard for wireless regional area networks. March 2008, http://grouper.ieee.org/groups/802/22/
Stevenson C, Chouinard G, Lei ZD, Hu WD, Shellhammer S, Caldwell W: IEEE 802.22: the first cognitive radio wireless regional area network standard. IEEE Communications Magazine 2009, 47(1):130-138.
Wireless Innovation Alliance 2008, http://www.wirelessinnovationalliance.com/
Sonnenschein A, Fishman PM: Radiometric detection of spreadspectrum signals in noise of uncertainty power. IEEE Transactions on Aerospace and Electronic Systems 1992, 28(3):654-660. 10.1109/7.256287
Sahai A, Cabric D: Spectrum sensing: fundamental limits and practical challenges. IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '05), November 2005, Baltimore, Md, USA
Tandra R, Sahai A: Fundamental limits on detection in low SNR under noise uncertainty. Proceedings of the International Conference on Wireless Networks, Communications and Mobile Computing (WirelessCom '05), June 2005, Maui, Hawaii, USA 1: 464-469.
Tandra R, Sahai A: SNR walls for signal detection. IEEE Journal on Selected Topics in Signal Processing 2008, 2(1):4-17.
Kay SM: Fundamentals of Statistical Signal Processing: Detection Theory. Volume 2. Prentice Hall, Upper Saddle River, NJ, USA; 1998.
Urkowitz H: Energy detection of unkown deterministic signals. Proceedings of the IEEE 1967, 55(4):523-531.
Chen HS, Gao W, Daut DG: Signature based spectrum sensing algorithms for IEEE 802.22 WRAN. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007, Glasgow, Scotland 6487-6492.
Gardner WA: Exploitation of spectral redundancy in cyclostationary signals. IEEE Signal Processing Magazine 1991, 8(2):14-36. 10.1109/79.81007
Gardner WA: Spectral correlation of modulated signals—part I: analog modulation. IEEE Transactions on Communications 1987, 35(6):584-595. 10.1109/TCOM.1987.1096820
Gardner WA, Brown WA III, Chen C-K: Spectral correlation of modulated signals—part II: digital modulation. IEEE Transactions on Communications 1987, 35(6):595-601. 10.1109/TCOM.1987.1096816
Han N, Shon SH, Joo JO, Kim JM: Spectral correlation based signal detection method for spectrum sensing in IEEE 802.22 WRAN systems. Proceedings of the 8th International Conference on Advanced Communication Technology, Febraury 2006, Phoenix Park, South Korea
Zeng YH, Liang Y-C: Eigenvalue based sensing algorithms. IEEE 802.22-06/0118r0, July 2006
Zeng YH, Liang Y-C: Maximum-minimum eigenvalue detection for cognitive radio. Proceedings of the 18th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece
Zeng YH, Liang Y-C: Eigenvalue-based spectrum sensing algorithms for cognitive radio. IEEE Transactions on Communications 2009, 57(6):1784-1793.
Bianchi P, Alfano JNG, Debbah M: Asymptotics of eigenbased collaborative sensing. Proceedings of the IEEE Information Theory Workshop (ITW '09), October 2009, Taormina, Sicily, Italy
Maida M, Najim J, Bianchi P, Debbah M: Performance analysis of some eigen-based hypothesis tests for collaborative sensing. Proceedings of the IEEE Workshop on Statistical Signal Processing, September 2009, Cardiff, Wales, UK
Penna F, Garello R, Spirito MA: Cooperative spectrum sensing based on the limiting eigenvalue ratio distribution in wishart matrices. IEEE Communications Letters 2009, 13(7):507-509.
Tian Z, Giannakis GB: A wavelet approach to wideband spectrum sensing for cognitive radios. Proceedings of the 1st International Conference on Cognitive Radio Oriented Wireless Networks and Communications (CROWNCOM '07), June 2007, Mykonos, Greece
Zeng YH, Liang Y-C: Covariance based signal detections for cognitive radio. Proceedings of the 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '07), April 2007, Dublin, Ireland 202-207.
Zeng YH, Liang Y-C: Spectrum-sensing algorithms for cognitive radio based on statistical covariances. IEEE Transactions on Vehicular Technology 2009, 58(4):1804-1815.
Zeng YH, Liang Y-C, Zhang R: Blindly combined energy detection for spectrum sensing in cognitive radio. IEEE Signal Processing Letters 2008, 15: 649-652.
Pasupathy S, Venetsanopoulos AN: Optimum active array processing structure and space-time factorability. IEEE Transactions on Aerospace and Electronic Systems 1974, 10(6):770-778.
Dogandzic A, Nehorai A: Cramer-rao bounds for estimating range, velocity, and direction with an active array. IEEE Transactions on Signal Processing 2001, 49(6):1122-1137. 10.1109/78.923295
Fishler E, Haimovich A, Blum R, Chizhik D, Cimini L, Valenzuela R: MIMO radar: an idea whose time has come. Proceedings of the IEEE National Radar Conference, April 2004, Philadelphia, Pa, USA 71-78.
Sheikhi A, Zamani A: Coherent detection for MIMO radars. Proceedings of the IEEE National Radar Conference, April 2007 302-307.
Varshney PK: Distributed Detection and Data Fusion. Springer, New York, NY, USA; 1996.
Unnikrishnan J, Veeravalli VV: Cooperative sensing for primary detection in cognitive radio. IEEE Journal on Selected Topics in Signal Processing 2008, 2(1):18-27.
Ganesan G, Li Y: Cooperative spectrum sensing in cognitive radio—part I: two user networks. IEEE Transactions on Wireless Communications 2007, 6: 2204-2213.
Ganesan G, Li Y: Cooperative spectrum sensing in cognitive radio—part II: multiuser networks. IEEE Transactions on Wireless Communications 2007, 6: 2214-2222.
Quan Z, Cui S, Sayed AH: Optimal linear cooperation for spectrum sensing in cognitive radio networks. IEEE Journal on Selected Topics in Signal Processing 2007, 2(1):28-40.
Mishra SM, Sahai A, Brodersen RW: Cooperative sensing among cognitive radios. Proceedings of the IEEE International Conference on Communications (ICC '06), June 2006, Istanbul, Turkey 4: 1658-1663.
Sun C, Zhang W, Letaief KB: Cluster-based cooperative spectrum sensing in cognitive radio systems. Proceedings of the 18th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece 2511-2515.
Ma J, Li Y: Soft combination and detection for cooperative spectrum sensing in cognitive radio networks. Proceedings of the IEEE Global Communications Conference (GlobeCom '07), November 2007, Washington, DC, USA
Peh E, Liang Y-C: Optimization for cooperative sensing in cognitive radio networks. Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC '07), March 2007, Hong Kong 27-32.
Liang Y-C, Zeng YH, Peh E, Hoang AT: Sensing-throughput tradeoff for cognitive radio networks. IEEE Transactions on Wireless Communications 2008, 7(4):1326-1337.
Tandra R, Mishra SM, Sahai A: What is a spectrum hole and what does it take to recognize one. IEEE Proceedings 2009, 97(5):824-848.
Akyildiz IF, Lee WY, Vuran MC, Mohanty S: Next generation/dynamic spectrum access/cognitive radio wireless networks: a survey. Computer Networks Journal 2006, 50(13):2127-2159. 10.1016/j.comnet.2006.05.001
Zhao Q, Sadler BM: A survey of dynamic spectrum access: signal processing, networking, and regulatory policy. IEEE Signal Processing Magazine 2007, 24: 79-89.
Ycek T, Arslan H: A survey of spectrum sensing algorithms for cognitive radio applications. IEEE Communications Surveys & Tutorials 2009, 11(1):116-160.
Sahai A, Mishra SM, Tandra R, Woyach KA: Cognitive radios for spectrum sharing. IEEE Signal Processing Magazine 2009, 26(1):140-145.
Ghasemi A, Sousa ES: Spectrum sensing in cognitive radio networks: requirements, challenges and design trade-offs. IEEE Communications Magazine 2008, 46(4):32-39.
Cabric D: Addressing the feasibility of cognitive radios. IEEE Signal Processing Magazine 2008, 25(6):85-93.
Oh SW, Naveen AAS, Zeng YH, et al.: White-space sensing device for detecting vacant channels in TV bands. Proceedings of the 3rd International Conference on Cognitive Radio Oriented Wireless Networks and Communications, (CrownCom '08), March 2008, Singapore
Oh SW, Le TPC, Zhang WQ, Naveen SAA, Zeng YH, Kua KJM: TV white-space sensing prototype. Wireless Communications and Mobile Computing 2008, 9: 1543-1551.
Zeng YH, Liang Y-C, Peh E, Hoang AT: Cooperative covariance and eigenvalue based detections for robust sensing. Proceedings of the IEEE Global Communications Conference (GlobeCom '09), December 2009, Honolulu, Hawaii, USA
Poor HV: An Introduction to Signal Detection and Estimation. Springer, Berlin, Germany; 1988.
Van-Trees HL: Detection, Estimation and Modulation Theory. John Wiley & Sons, New York, NY, USA; 2001.
Uchiyama H, Umebayashi K, Kamiya Y, et al.: Study on cooperative sensing in cognitive radio based ad-hoc network. Proceedings of the 18th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece
Pandharipande A, Linnartz JPMG: Perfromcane analysis of primary user detection in multiple antenna cognitive radio. Proceedings of the IEEE International Conference on Communications (ICC '07), June 2007, Glasgow, Scotland
Stoica P, Li J, Xie Y: On probing signal design for MIMO radar. IEEE Transactions on Signal Processing 2007, 55(8):4151-4161.
Giannakis GB, Hua Y, Stoica P, Tong L: Signal Processing Advances in Wireless & Mobile Communications. Prentice Hall PTR 2001., 1:
Lim TJ, Zhang R, Liang YC, Zeng YH: GLRT-based spectrum sensing for cognitive radio. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '08), December 2008, New Orleans, La, USA 4391-4395.
Zeng YH, Liang Y-C: Simulations for wireless microphone detection by eigenvalue and covariance based methods. IEEE 802.22-07/0325r0, July 2007
Peh E, Liang Y-C, Guan YL, Zeng YH: Optimization of cooperative sensing in cognitive radio networks: a sensing-throughput trade off view. IEEE Transactions on Vehicular Technology 2009, 58: 5294-5299.
Chair Z, Varshney PK: Optimal data fusion in multple sensor detection systems. IEEE Transactions on Aerospace and Electronic Systems 1986, 22(1):98-101.
Shellhammer S, Tandra R: Performance of the power detector with noise uncertainty. doc. IEEE 802.22-06/0134r0, July 2006
Clanton C, Kenkel M, Tang Y: Wireless microphone signal simulation method. IEEE 802.22-07/0124r0, March 2007
Tulino AM, Verdú S: Random Matrix Theory and Wireless Communications. Now Publishers, Hanover, Mass, USA; 2004.
Johnstone IM: On the distribution of the largest eigenvalue in principle components analysis. The Annals of Statistics 2001, 29(2):295-327. 10.1214/aos/1009210544
Johansson K: Shape fluctuations and random matrices. Communications in Mathematical Physics 2000, 209(2):437-476. 10.1007/s002200050027
Bai ZD: Methodologies in spectral analysis of large dimensional random matrices, a review. Statistica Sinica 1999, 9(3):611-677.
Zanella A, Chiani M, Win MZ: On the marginal distribution of the eigenvalues of wishart matrices. IEEE Transactions on Communications 2009, 57(4):1050-1060.
Tracy CA, Widom H: On orthogonal and symplectic matrix ensembles. Communications in Mathematical Physics 1996, 177(3):727-754. 10.1007/BF02099545
Tracy CA, Widom H: The distribution of the largest eigenvalue in the Gaussian ensembles. In Calogero-Moser-Sutherland Models. Edited by: van Diejen J, Vinet L. Springer, New York, NY, USA; 2000:461-472.
Dieng MRMLab Version 0.02, 2006, http://math.arizona.edu/?momar/ RMLab Version 0.02, 2006,
Huber PJ: Robust estimation of a location parameter. The Annals of Mathematical Statistics 1964, 35: 73-104. 10.1214/aoms/1177703732
Huber PJ: A robust version of the probability ratio test. The Annals of Mathematical Statistics 1965, 36: 1753-1758. 10.1214/aoms/1177699803
Zetterberg L-H: Signal detection under noise interference in a game situation. IRE Transactions on Information Theory 1962, 8: 47-57. 10.1109/TIT.1962.1057773
Poor HV: Robust matched filters. IEEE Transactions on Information Theory 1983, 29(5):677-687. 10.1109/TIT.1983.1056734
Kassam SA, Poor HV: Robust techniques for signal processing: a survey. Proceedings of the IEEE 1985, 73(3):433-482.
Rabideau DJ, Howard LC: Mitigation of digital array nonlinearities. Proceedings of the IEEE National Radar Conference, May 2001, Atlanta, Ga, USA 175-180.
Candès EJ, Romberg J, Tao T: Robust uncertainty principles: exact signal reconstruction from highly imcomplete frequency information. IEEE Transactions on Information Theory 2006, 52(2):489-509.
Candès EJ, Wakin MB: An introduction to compressive sampling. IEEE Signal Processing Magazine 2008, 21(3):21-30.
Donoho DL: Compressed sensing. IEEE Transactions on Information Theory 2006, 52(4):1289-1306.
Polo YL, Wang Y, Pandharipande A, Leus G: Compresive wideband spectrum sensing. Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '09), April 2009, Taipei, Taiwan
Zeng YH, Oh SW, Mo RH: Subcarrier sensing for distributed OFDMA in powerline communication. Proceedings of the IEEE International Conference on Communications (ICC '09), June 2009, Dresden, Germany
Quan Z, Cui S, Poor HV, Sayed AH: Collaborative wideband sensing for cognitive radios. IEEE Signal Processing Magazine 2008, 25(6):60-73.
Quan Z, Cui S, Sayed AH, Poor HV: Optimal multiband joint detection for spectrum sensing in dynamic spectrum access networks. IEEE Transactions on Signal Processing 2009, 57(3):1128-1140.
Pei Y, Liang Y-C, Teh KC, Li KH: How much time is needed for wideband spectrum sensing? to appear in IEEE Transactions on Wireless Communications
Zhang R, Liang Y-C: Exploiting hidden power-feedback loops for cognitive radio. Proceedings of the IEEE Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '08), October 2008 730-734.
Zhao G, Li YG, Yang C: Proactive detection of spectrum holes in cognitive radio. Proceedings of the IEEE International Conference on Communications (ICC '09), June 2009, Dresden, Germany
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zeng, Y., Liang, YC., Hoang, A.T. et al. A Review on Spectrum Sensing for Cognitive Radio: Challenges and Solutions. EURASIP J. Adv. Signal Process. 2010, 381465 (2010). https://doi.org/10.1155/2010/381465
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/381465
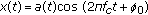 . It has cyclic frequencies at
. It has cyclic frequencies at 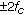 .
. . It usually has cyclic frequencies at
. It usually has cyclic frequencies at 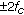 . The characteristics of the SCD function at cyclic frequency
. The characteristics of the SCD function at cyclic frequency 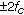 depend on
depend on 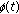 .
.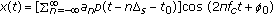 . It has cyclic frequencies at
. It has cyclic frequencies at 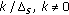 and
and 
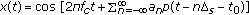 . For BPSK, it has cyclic frequencies at
. For BPSK, it has cyclic frequencies at 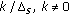 , and
, and 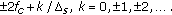 For QPSK, it has cycle frequencies at
For QPSK, it has cycle frequencies at  .
.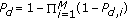 and
and  , respectively, where
, respectively, where 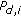 and
and  are the probability of detection and probability of false alarm for user
are the probability of detection and probability of false alarm for user  , respectively.
, respectively.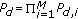 and
and 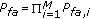 , respectively.
, respectively. out of
out of  " Rule: If and only if
" Rule: If and only if 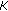 decisions or more are "1"s, the final decision is "1." This includes "Logical-OR (LO)" (
decisions or more are "1"s, the final decision is "1." This includes "Logical-OR (LO)" ( ), "Logical-AND (LA)" (
), "Logical-AND (LA)" (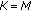 ), and "Majority" (
), and "Majority" ( ) as special cases [
) as special cases [


