- Review Article
- Open access
- Published:
A Human Gait Classification Method Based on Radar Doppler Spectrograms
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 389716 (2010)
Abstract
An image classification technique, which has recently been introduced for visual pattern recognition, is successfully applied for human gait classification based on radar Doppler signatures depicted in the time-frequency domain. The proposed method has three processing stages. The first two stages are designed to extract Doppler features that can effectively characterize human motion based on the nature of arm swings, and the third stage performs classification. Three types of arm motion are considered: free-arm swings, one-arm confined swings, and no-arm swings. The last two arm motions can be indicative of a human carrying objects or a person in stressed situations. The paper discusses the different steps of the proposed method for extracting distinctive Doppler features and demonstrates their contributions to the final and desirable classification rates.
1. Introduction
In the past few years, human gait analysis has received significant interest due to its numerous applications, such as border surveillance, video understanding, biometric identification, and rehabilitation engineering. Besides the advances in vision-based gait recognition technology, there is a large amount of research concerned with the development of automatic radar gait recognition systems. Radars have certain advantages over optical-based systems in that it can operate in all types of weather, is insensitive to lighting conditions and the size of the object, and can penetrate clothes. The general concept of radar-based systems is to transmit an electromagnetic wave at a certain range of frequencies and analyze the radar return signal to estimate the velocity of a moving object by measuring the frequency shift of the wave radiated or scattered by the object, known as the Doppler effect. For an articulated object such as a walking person, the motion of various components of the body including arms and legs induces frequency modulation on the returned signal and generates sidebands about the Doppler frequency, referred to as micro-Doppler signatures. These micro-Doppler signatures have been studied in a number of publications [1–4] using joint time-frequency representations.
Signals characterized with multiple components having different frequency laws leave distinct features when examined in the time-frequency domain [5]. Therefore, to extract useful information, a type of joint time-frequency analysis is usually performed on the radar data to convert a one-dimensional nonstationary temporal signal into a two-dimensional joint-variable distribution [6–9]. When presenting the signal power distribution over time and frequency, the time-frequency signal representation can be cast as a typical image in which the two spatial axes are replaced by the time and frequency variables. This similarity invites the application of image-based classification techniques to non-stationary signal analysis.
In this paper, we apply an image processing method for classification of people based on the Doppler signatures they produce when walking. In this respect, we consider received radar data of human walking motion and represent the corresponding signal in the time-frequency domain using spectrograms. Herein, three types of human walking motion are considered: ( ) free-arm motion (FAM) characterized by swinging of both arms, (
) free-arm motion (FAM) characterized by swinging of both arms, ( ) partial-arm motion (PAM), which corresponds to a motion of only one arm, and (
) partial-arm motion (PAM), which corresponds to a motion of only one arm, and ( ) no-arm motion (NAM), which corresponds to no motion of both arms. The NAM is referred to as a stroller or sauntere [2]. The last two classes are commonly associated with a person walking with his/her hand(s) in the trouser pockets or a person carrying light small or heavy large objects, respectively. All three categories are considered important for police and law enforcement, especially when humans are behind opaque material, that is, inside buildings and in enclosed structures, or they are monitored while moving in city canyons and street corners.
) no-arm motion (NAM), which corresponds to no motion of both arms. The NAM is referred to as a stroller or sauntere [2]. The last two classes are commonly associated with a person walking with his/her hand(s) in the trouser pockets or a person carrying light small or heavy large objects, respectively. All three categories are considered important for police and law enforcement, especially when humans are behind opaque material, that is, inside buildings and in enclosed structures, or they are monitored while moving in city canyons and street corners.
Existing human gait classification methods for radar systems can be categorized as parametric and nonparametric approaches. In parametric approaches, explicit parameters are extracted from the respective time-frequency distributions and used as features for classification [10]. Some important features could be the periods characterizing the repetitive arm and leg motions, the Doppler frequency of the torso, which is indicative of walking or running motion, the radar cross-section (RCS), the relative times of positive and negative Doppler describing the forward and backward swings, among others. In nonparametric approaches, portions or segments of the time-frequency distributions, or their subspace representations, are employed as features, followed by a classifier [11, 12].
The proposed method for the above gait classification problem is nonparametric in nature. It is based upon a hierarchical image classification architecture, which has recently been developed for visual pattern classification [13]. Instead of processing optical images, the time-frequency representation of Doppler is used as input to the image classification architecture, which comprises a set of nonlinear directional and adaptive two-dimensional filters, followed by a classifier. We show that each stage of the proposed architecture captures salient features from the Doppler spectrograms which are useful for classification of human motions.
The remainder of the paper is organized as follows. Section 2 describes the application of Short-Time Fourier Transform (STFT) technique to capture the micro-Doppler signatures of the three types of arm motion, FAM, PAM, and NAM. Section 3 presents the proposed classification method which consists of a cascade of directional filters and adaptive filters. Section 4 presents experimental results demonstrating that the proposed image classification technique can be successfully applied to time-frequency signal representations. Finally, concluding remarks are given in Section 5.
2. Human Motion Signatures inTime Frequency
The proposed classification technique is applied to real data collected in the Radar Imaging Lab, Center for Advanced Communications, Villanova University, USA. The radar is a continuous wave (CW) operating at 2.4 GHz and with direct line of sight to the target. The data for five persons (labelled as A, B, C, D, and E) were collected and sampled at 1 kHz with a transmit power level of 5 dBm. The motion of each subject was recorded for 20 seconds, with the person moving forwards (towards the radar) and backwards. When a person is walking, various components of the body, such as the torso, legs, and arms have different velocities, and the signal reflected from these components will have a Doppler shift. To capture the Doppler frequency at various instances of time, a joint time-frequency analysis method is used.
The spectrogram  , which shows how the signal power varies with time
, which shows how the signal power varies with time  and frequency
and frequency  , is used to analyze the time-varying micro-Doppler signatures of human motion. It is obtained by computing the Short-Time Fourier Transform (STFT) of the data
, is used to analyze the time-varying micro-Doppler signatures of human motion. It is obtained by computing the Short-Time Fourier Transform (STFT) of the data  with a hamming window
with a hamming window  which is given by
which is given by

Figures 1(a)–1(c) illustrate the Doppler spectrograms of the three arm motions: PAM, FAM, and NAM. The Doppler frequency is displayed on the vertical axis and the time on the horizontal axis. The amplitude of the returned signal is color coded with red being the highest intensity and blue the lowest intensity. The spine of each plot represents the torso motion, that is, the speed of the subject whereas the positive and negative Dopplers correspond to the subject moving toward or away from the radar, respectively. The periodic peaks in the plots denote the arms, legs, andfeetmotions.For instance, in Figure 1(b), fast arm motions are shown as large peaks whereas the foot and leg motions appear as smaller peaks. Note that during a gait cycle the arm motion produces a positive and a negative Doppler, and the leg motion generates positive Doppler for a subject moving towards the radar and a negative Doppler for a subject moving backwards facing the radar [12]. Figure 1(c) depicts the composite Doppler when the subject is swinging both arms while walking. These spectrograms clearly show a difference between human gait signatures. Hence, the objective of this paper is to apply an image-based classification technique to detect the intrinsic characteristics of the gait signatures and subsequently extract salient features for classifying different human activities.
3. Hierarchical Image ClassificationArchitecture (HICA)
In [10], the classification of human activity was achieved by first extracting a set of features from the entire Doppler spectrogram, then feeding them to a Support Vector Machine (SVM) classifier; naturally, the performance of the classifier depends on the type and number of features selected as inputs to the classifier. In this paper, classification of human walking motion is achieved using a hierarchical image classification architecture (HICA) that operates directly on short time-frequency windows. The raw spectrogram windows are processed and classified automatically into one of three types of arm motion: FAM, PAM, and NAM. The HICA, shown in Figure 2, consists of three processing stages. The first stage consists of directional filters to extract motion energy and directional contrast in the time-frequency plane. The role of the second stage is to learn the intrinsic features characterizing the different classes of arm motion during human walk. The last stage is a classifier that uses as input the learned feature of the second stage. The first two stages employ nonlinear processing inspired by the biophysical mechanism of shunting inhibition, which plays an important role in many visual functions [14, 15], and has been adopted in machine learning [16–18] and image processing [19, 20]. In the following, we describe the three processing stages in more detail.
3.1. Stage 1—Oriented Feature Extraction
A number of techniques have been developed for designing directional filters [21–23] and steerable filters [24, 25]. However, most of these filters are linear filters, which are not suitable for extracting directional contrast. Therefore, we have developed nonlinear directional filters inspired by the biophysical mechanism of shunting inhibition to extract motion energy and directional contrast from the two-dimensional (2D) time-frequency plane. These filters, which are based on feed-forward shunting inhibition, are nonrecursive. The response of the  th filter, oriented along direction
th filter, oriented along direction  , is given by
, is given by

where  is a 2D input window from the spectrogram
is a 2D input window from the spectrogram  ,
,  and
and  are 2D convolution masks, and
are 2D convolution masks, and  denotes the 2D convolution operation. We should note that the division operation in (2) refers to element-by-element matrix division. The number of filters,
denotes the 2D convolution operation. We should note that the division operation in (2) refers to element-by-element matrix division. The number of filters,  , in the first stage is chosen according to the complexity of the given task; each filter is oriented along an angle
, in the first stage is chosen according to the complexity of the given task; each filter is oriented along an angle  (
( ). The convolution mask
). The convolution mask  is obtained from the first-order derivative of a Gaussian kernel. For a given direction
is obtained from the first-order derivative of a Gaussian kernel. For a given direction  , the first-order derivative Gaussian kernel is defined as
, the first-order derivative Gaussian kernel is defined as

where


The second convolution mask,  , is simply defined as an isotropic Gaussian filter, given by
, is simply defined as an isotropic Gaussian filter, given by

In addition to motion energy extraction, the proposed classification model is designed to be robust to small translations and geometric distortions in the input image. This is achieved by reducing the spatial resolution of the filter outputs through downsampling. The subsampling operation employed in the first stage, illustrated in Figure 3 , decomposes each filter output
, decomposes each filter output  into four smaller maps,
into four smaller maps,

The first downsampled map  is formed from the odd rows and odd columns in
is formed from the odd rows and odd columns in  ; the second downsampled map
; the second downsampled map  is formed from the odd rows and even columns, and so on. The rationale of this downsampling process is to lower the spatial resolution of the filter output without discarding too much information.
is formed from the odd rows and even columns, and so on. The rationale of this downsampling process is to lower the spatial resolution of the filter output without discarding too much information.
Furthermore, inspired by the center-surround receptive fields and the On-Off processing which takes place in the early stages of the mammalian visual system, each downsampled map is divided into an On-response map and an Off-response map by simply thresholding its response,

Basically, for the on-response map, all negative entries are set to  whereas for the off-response map, positive entries are set to
whereas for the off-response map, positive entries are set to  and the entire map is then negated. At the end of Stage
and the entire map is then negated. At the end of Stage  , the features in each sub-sampled map are normalized, using the following transformation:
, the features in each sub-sampled map are normalized, using the following transformation:

where  is the mean value of the absolute response of the output map of the directional filter before downsampling.
is the mean value of the absolute response of the output map of the directional filter before downsampling.
3.2. Stage 2—Learning Intrinsic Motion Features
In Stage 2 a set of adaptive filters is used to learn the characteristic features of human motion that can easily be classified into various human motion types. Therefore, the output maps from each directional filter in Stage  are processed by exactly two filters in Stage
are processed by exactly two filters in Stage  ; one filter for on-response maps and one for the off-response maps. This implies that the second stage has double the number of filters in Stage 1;
; one filter for on-response maps and one for the off-response maps. This implies that the second stage has double the number of filters in Stage 1;  . Let
. Let  be the
be the  th downsampled input map to the
th downsampled input map to the  th filter of Stage
th filter of Stage  . The response of Stage 2 filter is given by
. The response of Stage 2 filter is given by

where  and
and  are 2D convolution masks,
are 2D convolution masks,  ,
,  ,
,  , and
, and  are bias terms,
are bias terms,  is a matrix of ones, and
is a matrix of ones, and  and
and  are activation functions. All filter parameters in the second stage are trainable; their desired values are determined using a learning algorithm. The activation functions and biases are added to facilitate convergence of the learning algorithm. During the training phase, a constraint is imposed on the bias term in the denominator of (10) so as to avoid division by zero:
are activation functions. All filter parameters in the second stage are trainable; their desired values are determined using a learning algorithm. The activation functions and biases are added to facilitate convergence of the learning algorithm. During the training phase, a constraint is imposed on the bias term in the denominator of (10) so as to avoid division by zero:

where  denotes the infimum or the greatest lower bound of the activation function
denotes the infimum or the greatest lower bound of the activation function  , and
, and  is a small positive constant. Similarly, a sub-sampling operation is performed on the four output maps of each adaptive filter. The four output maps are compressed and arranged into a vector form by averaging each nonoverlapping block of size
is a small positive constant. Similarly, a sub-sampling operation is performed on the four output maps of each adaptive filter. The four output maps are compressed and arranged into a vector form by averaging each nonoverlapping block of size  into a single output signal. This process is repeated for all output maps produced at stage 2 to generate a single column feature vector, as shown in Figure 3
into a single output signal. This process is repeated for all output maps produced at stage 2 to generate a single column feature vector, as shown in Figure 3 :
:

3.3. Stage 3—Classifier
The feature vector extracted by Stage  is sent to a classifier, which may be any generic classifier. However, in this paper, a simple linear classifier is used to demonstrate the effectiveness of the HICA in learning the intrinsic motion characteristics. Each class is represented by a linear element, which implements a hyperplane in the feature space. Therefore, the response of the
is sent to a classifier, which may be any generic classifier. However, in this paper, a simple linear classifier is used to demonstrate the effectiveness of the HICA in learning the intrinsic motion characteristics. Each class is represented by a linear element, which implements a hyperplane in the feature space. Therefore, the response of the  th output element, denoted by
th output element, denoted by  , is given by
, is given by

where  is an adjustable weight,
is an adjustable weight,  is an adjustable bias term,
is an adjustable bias term,  is the
is the  th element of the input feature vector
th element of the input feature vector  , and
, and  is the number of features. The output class label
is the number of features. The output class label  , corresponding to the
, corresponding to the  th input pattern, is determined as
th input pattern, is determined as

3.4. Training Method
Consider a training set of  input patterns
input patterns  and
and  corresponding desired outputs
corresponding desired outputs  , where
, where  is the desired output vector associated with the
is the desired output vector associated with the  th input pattern. The desired output is defined as a column vector
th input pattern. The desired output is defined as a column vector  , where 1 represents the input class. The adaptation of the parameters of the adaptive filters and the classifier can be formulated as an optimization problem, which minimizes the error between the actual responses of the classifier and the desired outputs. Although other error functions could be used, for simplicity, the error function chosen herein is the mean square error (MSE);
, where 1 represents the input class. The adaptation of the parameters of the adaptive filters and the classifier can be formulated as an optimization problem, which minimizes the error between the actual responses of the classifier and the desired outputs. Although other error functions could be used, for simplicity, the error function chosen herein is the mean square error (MSE);

where  and
and  are the
are the  th element of the desired output vector
th element of the desired output vector  and the actual response
and the actual response  , respectively, and
, respectively, and  is the number of arm motions, that is,
is the number of arm motions, that is,  . The Levenberg-Marquardt (LM) algorithm [26] is used to learn the optimum adaptive filter parameters in Stage 2 and the parameters of the classifier in Stage 3. The LM algorithm is a fast and effective training method; it combines the stability of the gradient descent with the speed of Newton algorithm. Given that all parameters of the adaptive filters and the linear classifier are arranged as a column vector,
. The Levenberg-Marquardt (LM) algorithm [26] is used to learn the optimum adaptive filter parameters in Stage 2 and the parameters of the classifier in Stage 3. The LM algorithm is a fast and effective training method; it combines the stability of the gradient descent with the speed of Newton algorithm. Given that all parameters of the adaptive filters and the linear classifier are arranged as a column vector,  . The main steps of the LM algorithm are given as follows.
. The main steps of the LM algorithm are given as follows.
Step 1.
Initialize the trainable coefficients of nonlinear filters in Stage  and the parameters of the linear classifier in Stage
and the parameters of the linear classifier in Stage  with random values from a uniform distribution in the range
with random values from a uniform distribution in the range  .
.
Step 2.
Perform forward computation to find the outputs of each stage in response to the training patterns.
Step 3.
Calculate the weight update at iteration  as
as

where  is the Jacobian of the error function
is the Jacobian of the error function  ,
,  is the identity matrix, and
is the identity matrix, and  is a regularization term to avoid the singularity problem. During training, the regularization parameter is increased or decreased by a factor of ten, depending on the decrease or increase of the MSE, respectively. The Jacobian matrix can be computed from a modified version of the error-backpropagation algorithm, which is explained in [27].
is a regularization term to avoid the singularity problem. During training, the regularization parameter is increased or decreased by a factor of ten, depending on the decrease or increase of the MSE, respectively. The Jacobian matrix can be computed from a modified version of the error-backpropagation algorithm, which is explained in [27].
Step 4.
Repeat Steps 2 to 3 until the maximum number of training epochs is reached or the error is below a predefined limit.
4. Experimental Methods and Results
Real data is collected from five subjects (labelled A to E) walking with three different arm motions: NAM, PAM and FAM. Two sets of data were collected with subjects moving at  and
and  incidence angle with respect to the line of sight of the radar system. Figure 4 presents the spectrograms of one-arm swing for a subject moving at
incidence angle with respect to the line of sight of the radar system. Figure 4 presents the spectrograms of one-arm swing for a subject moving at  and
and  , respectively. The Doppler spectrogram of each radar trace is computed using the STFT with a hamming window. A range of window lengths were considered and investigated. In all experiments presented in this paper, Subjects A and B are used for training and Subjects C, D, and E are used for testing.
, respectively. The Doppler spectrogram of each radar trace is computed using the STFT with a hamming window. A range of window lengths were considered and investigated. In all experiments presented in this paper, Subjects A and B are used for training and Subjects C, D, and E are used for testing.
Before the spectrogram is computed, the radar trace is downsampled by a factor of two to reduce the amount of data to be processed. Furthermore, the spectrogram is normalized by dividing by its maximum value. Overlapping spectrogram windows of size  are used for training and testing the HICA presented in Section 3. The spectrogram windows are centred at the location of the torso, that is, at the maximum magnitude spectrum for each given time interval. There is a tradeoff between the input window size and the HICA classification performance; a too small window does not allow the HICA to learn the salient features of each motion, and a too large window increases the complexity of the HICA, which affects its generalization ability. Therefore, the input window is chosen as the minimum window size that achieves good classification performance. Previous studies on visual pattern recognition problems showed that the HICA achieves good classification performance when using convolution masks of size
are used for training and testing the HICA presented in Section 3. The spectrogram windows are centred at the location of the torso, that is, at the maximum magnitude spectrum for each given time interval. There is a tradeoff between the input window size and the HICA classification performance; a too small window does not allow the HICA to learn the salient features of each motion, and a too large window increases the complexity of the HICA, which affects its generalization ability. Therefore, the input window is chosen as the minimum window size that achieves good classification performance. Previous studies on visual pattern recognition problems showed that the HICA achieves good classification performance when using convolution masks of size  for each adaptive filter in Stage 2 [28, 29]. Thus, the size of the convolution masks
for each adaptive filter in Stage 2 [28, 29]. Thus, the size of the convolution masks  and
and  is set to
is set to  in all experiments, and the exponential and hyperbolic tangent activation functions are chosen for
in all experiments, and the exponential and hyperbolic tangent activation functions are chosen for  and
and  , respectively. For Stage 1 the directional filters are designed with kernel size of
, respectively. For Stage 1 the directional filters are designed with kernel size of  and
and  .
.
The optimum configuration of the HICA depends on a number of factors, including the number of directional filters used in Stage 1, the time/frequency resolution of the spectrogram window, and the classifier type for Stage 3. Several experiments were conducted to determine the effects of these factors on the classification performance. The classification rate is used as a measure of performance, which is computed as a ratio of the number of correctly classified windows over the total number of test windows. The optimum parameters are chosen when the maximum classification rate is achieved on a validation set. The effects of the various parameters are investigated using the  incidence angle motion data only. The experimental results are presented in the following three subsections.
incidence angle motion data only. The experimental results are presented in the following three subsections.
4.1. Performance of Various HICA Configurations
To determine the right HICA configuration, several models comprising a varying number of directional filters are trained with the LM algorithm, and their classification performances are recorded. The number of directional filters in Stage 1 is varied from 2 to 10 with a linear classifier employed in Stage 3. Figure 5 shows the variations of the classification rate as a function of the number of directional filters in Stage 1. With only two filters oriented at  and
and  , the proposed method achieves around 93% classification rate. With more filters tuned to extract features at finer orientations, the classification performance improves significantly. For example, with seven directional filters, the classification performance is increased above 98%. However, there is a tradeoff between the number of filters and classifier performance. As the number of directional filters increases, the number of free parameters increases accordingly, thereby increasing the complexity of the classifier.
, the proposed method achieves around 93% classification rate. With more filters tuned to extract features at finer orientations, the classification performance improves significantly. For example, with seven directional filters, the classification performance is increased above 98%. However, there is a tradeoff between the number of filters and classifier performance. As the number of directional filters increases, the number of free parameters increases accordingly, thereby increasing the complexity of the classifier.
4.2. Effect of Time/Frequency Resolution
In the proposed classification method, the input is a 2D time-frequency window of the spectrogram; its classification performance is affected by both the time and frequency resolutions. In order to determine the optimum input window size, the HICA should be trained with varying input signal length. One way of conducting this experiment is to implement several classification models with different input sizes; however, this process is computationally expensive as the number of free parameters of the model is related to the input size. Another way is to downsample the spectrogram by different scale factors along the time-axis and train the classification method with a fixed input size, for example,  . If the spectrogram is downsampled by a factor
. If the spectrogram is downsampled by a factor  , then for a
, then for a  input window, the actual length of the input signal (in seconds) is
input window, the actual length of the input signal (in seconds) is  , where the factor of
, where the factor of  is due to the sub-sampling operation performed on the signal before applying the STFT. To reduce aliasing effects due to downsampling, the spectrogram is smoothed with a Gaussian filter along the frequency axis and the time axis. Note that the spectrogram is also downsampled along the frequency axis so that the periodic peaks are captured by the input window. Figure 7 records the performance of the proposed method with respect to the duration of the input signal. The plot indicates that the maximum classification rate is obtained with a window length of 4.7 seconds. It is worth noting that the spectrogram of 4.7 seconds window contains the walking motion together with the periodicity of the arm swings, as shown in Figure 6. For a shorter window, for example, 2.3 seconds, the classification rate is 88%. In principle, the classification performance should improve as the window length increases (more information is available to the classifier). However, the plot shows a decrease in classification performance; this is because to process a longer signal, the spectrogram has to be severely downsampled, leading to loss of vital information from the input window.
is due to the sub-sampling operation performed on the signal before applying the STFT. To reduce aliasing effects due to downsampling, the spectrogram is smoothed with a Gaussian filter along the frequency axis and the time axis. Note that the spectrogram is also downsampled along the frequency axis so that the periodic peaks are captured by the input window. Figure 7 records the performance of the proposed method with respect to the duration of the input signal. The plot indicates that the maximum classification rate is obtained with a window length of 4.7 seconds. It is worth noting that the spectrogram of 4.7 seconds window contains the walking motion together with the periodicity of the arm swings, as shown in Figure 6. For a shorter window, for example, 2.3 seconds, the classification rate is 88%. In principle, the classification performance should improve as the window length increases (more information is available to the classifier). However, the plot shows a decrease in classification performance; this is because to process a longer signal, the spectrogram has to be severely downsampled, leading to loss of vital information from the input window.
Another experiment was also conducted to investigate the influence of the STFT frequency resolution on the classification performance. Different window lengths are used to compute the spectrogram, starting from 64 msec to 960 msec. We should note that although the frequency resolution improves with the length of the STFT window, the spectrogram becomes blurry in time (see Figure 8). In order to determine the "optimum" frequency resolution, we train and test several HICAs using different STFT window lengths. Figure 9 shows the tradeoff between time and frequency resolution of STFT on the classification performance. With either good time resolution or good frequency resolution, the proposed method achieves moderate classification rates. At 512 msec, the classification method achieves the best classification accuracy. This implies that to classify human motions from spectrogram, a balance of good time and frequency resolution is required.
4.3. Performance of the Feature Extraction Stages
The proposed method comprises two feature extraction stages: Stage 1 extracts elementary features using nonlinear directional filters whereas Stage 2 employs adaptive nonlinear filters to refine the feature extraction process. The outputs of seven directional filters applied to the Doppler spectrogram of one-arm motion are presented in Figure 10. The figure shows how the different filters emphasize the details of the spectrogram in different directions. This is clearly highlighted by the output responses of the directional filters. For example, at  orientation, the filter differentiates along the horizontal direction, thereby emphasizing the vertical features. The outputs of the adaptive filters of Stage 2 are presented in Figure 11. It is clear from the figure how the micro-Doppler features of the spectrogram are further underlined in Stage 2.
orientation, the filter differentiates along the horizontal direction, thereby emphasizing the vertical features. The outputs of the adaptive filters of Stage 2 are presented in Figure 11. It is clear from the figure how the micro-Doppler features of the spectrogram are further underlined in Stage 2.
To determine the effectiveness of the extracted features for classification, a linear classifier is trained separately on the inputs computed from the raw spectrogram (input windows), Stage 1 features, and Stage 2 features. The results presented in Table 1 show that it is more reliable to classify features extracted by the HICA than the raw spectrogram input. Based on the "raw" spectrogram input, a linear classifier can merely achieve 49.6% on the test set. However, using the features extracted by the nonlinear filters in the first stage, the classification rate is improved to 71.0%. Further processing by the adaptive filters in Stage 2 yields 98.8% classification accuracy.
For further analysis, a confusion matrix of the HICA is depicted in Table 2. The main diagonal of the matrix lists the correct classification rate for each human motion. The off-diagonal entries indicate misclassification rates. Entries in the third row show that the proposed method has some difficulty in distinguishing between partial arm motion (PAM) and free-arm motion (FAM). However, the overall result indicates that the HICA is an effective classification method for human motions from Doppler spectrograms.
 incidence angle.
incidence angle.4.4. Comparison with Other Classifiers
In this subsection, the performance of the proposed HICA method is compared with those of two well-known classifiers, namely multilayer perceptron (MLP) and Support Vector Machine (SVM). Herein, we employ the SVM toolbox developed by Chang and Lin [30]. The parameters of the SVM with RBF kernel are obtained by performing a grid-search on  and
and  using cross-validation based on the training set whereas for MLP several networks with different number of sigmoid neurons in the hidden layer are trained, and the network with the best classification performance on the validation set is selected. For MLP and SVM, the training and testing samples are pre-processed by the contrast normalization technique given by (9). Table 3 lists the best classification results of the MLP and SVM, together with those obtained by the proposed method. The SVM and MLP achieve 88% and 79.7% classification rates, respectively, whereas the proposed method has 98.8% classification rate. It is clear from these results that the HICA has better performance than the MLP and SVM. In [10], for example, the authors computed six salient features from the spectrogram and used them as input to the SVM. However, this approach relies on the expert knowledge of the user to extract the best features possible. In the proposed approach, the feature extraction process is automatically handled during training.
using cross-validation based on the training set whereas for MLP several networks with different number of sigmoid neurons in the hidden layer are trained, and the network with the best classification performance on the validation set is selected. For MLP and SVM, the training and testing samples are pre-processed by the contrast normalization technique given by (9). Table 3 lists the best classification results of the MLP and SVM, together with those obtained by the proposed method. The SVM and MLP achieve 88% and 79.7% classification rates, respectively, whereas the proposed method has 98.8% classification rate. It is clear from these results that the HICA has better performance than the MLP and SVM. In [10], for example, the authors computed six salient features from the spectrogram and used them as input to the SVM. However, this approach relies on the expert knowledge of the user to extract the best features possible. In the proposed approach, the feature extraction process is automatically handled during training.
4.5. Classification of Short-Time Segments
Several existing methods use the entire frame to classify the motion of a subject. For example, Mobasseri and Amin [11] used principal component analysis (PCA) on the same data set to extract features from the spectrogram and applied a quadratic classifier based on the mahalanobis distance for classifying the spectrogram of human motion. When extracting feature vector parallel to the frequency axis, they achieved 82.5% for classifying no-arm motion (NAM), 69.1% for classifying PAM and, 70.7% for classifying FAM. However, when the feature vectors are computed parallel to the time axis (Doppler snapshots), the classification performance is increased to 100% for PAM, 98.3% for FAM, and 100% for NAM. This improvement is due to large changes in the Doppler frequency across time.
The proposed classification method, on the other hand, has the capability to classify short-time windows, segments or the entire frame (spectrogram). Herein, a segment of the spectrogram is defined as a set of overlapping short-time windows and the entire frame is represented as a set of overlapping segments. Based on the optimum window size (4.7 sec), a segment of the spectrogram is classified by processing its overlapping windows to produce a set of classification scores, which are then aggregated using the majority voting rule. Figure 12 shows the accuracy of the proposed method of classifying input segment of different lengths. For example, an input segment of 4.7 sec (i.e., the same time duration as a short-time window), the classification rate is 98.8%, and increasing the length of the segment to 5.54 sec, the classification rate increases to 99.37%. Perfect classification is achieved when the length of the segment is 6.22 sec. Applying the majority voting rule on the classification scores of all short-time windows extracted from the entire frame, the proposed method achieves perfect result in classifying the Doppler spectrogram.
4.6. Oblique View Angle: 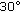 to the Axis of the Antenna
to the Axis of the Antenna
In practical situations, the target can move at any directions with respect to the radar system. As the aspect angle increases from  to
to  , the Doppler signal that returns from the arm further from the radar becomes weaker due to the body occlusion; this problem is depicted in Figures 4(b) and 13. With the micro-Doppler signature of one arm subdued, classification errors are likely to rise. In this experiment, we assume that Stages 1 and 2 have already been designed to extract salient features; in this case, the adaptive filters of Stage 2 are trained on the
, the Doppler signal that returns from the arm further from the radar becomes weaker due to the body occlusion; this problem is depicted in Figures 4(b) and 13. With the micro-Doppler signature of one arm subdued, classification errors are likely to rise. In this experiment, we assume that Stages 1 and 2 have already been designed to extract salient features; in this case, the adaptive filters of Stage 2 are trained on the  motion with a linear classifier. Here, only the classifier is retrained and tested on radar data collected at
motion with a linear classifier. Here, only the classifier is retrained and tested on radar data collected at  to the axis of the radar. The training samples are from Subjects A and B, and the test samples are from Subjects C, D, and E. Three classifiers were considered: a linear, MLP, and SVM classifier. For short-time windows, the classification performances of the three classifiers are given in Table 4. Based on a linear classifier, only 77.4% classification rate is achieved when classifying arm motions collected at an oblique angle. Using a nonlinear classifier, such as the MLP or SVM, the classification performance is improved to over 80%. From the confusion matrix, depicted in Table 5, the HICA method with a MLP classifier achieves 91.2% for FAM, whereas for PAM and NAM, the classification rates are 77.3% and 88.2%, respectively. However, when the spectrogram is divided into a set of 170 overlapping short-time windows and a majority voting rule is applied on their classification scores, the entire frame is correctly classified.
to the axis of the radar. The training samples are from Subjects A and B, and the test samples are from Subjects C, D, and E. Three classifiers were considered: a linear, MLP, and SVM classifier. For short-time windows, the classification performances of the three classifiers are given in Table 4. Based on a linear classifier, only 77.4% classification rate is achieved when classifying arm motions collected at an oblique angle. Using a nonlinear classifier, such as the MLP or SVM, the classification performance is improved to over 80%. From the confusion matrix, depicted in Table 5, the HICA method with a MLP classifier achieves 91.2% for FAM, whereas for PAM and NAM, the classification rates are 77.3% and 88.2%, respectively. However, when the spectrogram is divided into a set of 170 overlapping short-time windows and a majority voting rule is applied on their classification scores, the entire frame is correctly classified.
 data, using features trained with
data, using features trained with  data.
data. using a MLP as classifier in Stage 3 of HICA.
using a MLP as classifier in Stage 3 of HICA.5. Conclusion
A three-stage classification method employing both fixed directional and adaptive filters, in addition to a linear classifier, is introduced for classifying various types of human walking. The filters are applied in the time-frequency domain which depicts the Doppler signal power distribution over time and frequency. Three types of arm motion are considered: free-arm swings, one-arm confined swings, and two-arm confined swings. The proposed method determines the optimum time-frequency window for training and testing, and is able to detect and extract distinct Doppler features from the spectrogram. The data used for testing and training correspond to five subjects moving towards and away from the radar with  and
and  aspect angle, and with nonobstructed line of sight. The paper shows the importance of each stage of the classification method in improving the classification rates. The attractiveness of the proposed method lies in its robustness to data misalignments, forward/backward walking motions, including the acceleration-deceleration phases exhibited when turning, and to the specific quadratic distribution used for time-frequency signal representations.
aspect angle, and with nonobstructed line of sight. The paper shows the importance of each stage of the classification method in improving the classification rates. The attractiveness of the proposed method lies in its robustness to data misalignments, forward/backward walking motions, including the acceleration-deceleration phases exhibited when turning, and to the specific quadratic distribution used for time-frequency signal representations.
References
Geisheimer JL, Greneker EF, Marshall WS: High-resolution Doppler model of the human gait. Radar Sensor Technology and Data Visualization, April 2002, Orlando, Fla, USA, Proceedings of SPIE 4744: 8-18.
Van Dorp P, Groen FCA: Human walking estimation with radar. IEE Proceedings: Radar, Sonar and Navigation 2003, 150(5):356-366. 10.1049/ip-rsn:20030568
Chen VC: Analysis of radar micro-Doppler signature with time-frequency transform. Proceedings of IEEE Signal Processing Workshop on Statistical Signal and Array Processing (SSAP '00), 2000, Pocono, Pa, USA 463-466.
Smith GE, Woodbridge K, Baker CJ: Multistatic micro-Doppler signature of personnel. Proceedings of IEEE Radar Conference (RADAR '08), May 2008
Cohen L: Time-Frequency Analysis. Prentice Hall, Upper Saddle River, NJ, USA; 1995.
Amin M, Sarabandi K: Special issue on remote sensing of building interior. IEEE Transactions on Geoscience and Remote Sensing 2009, 47(5):1267-1268.
Amin M: Special issue on advances in indoor radar imaging. Journal of the Franklin Institute 2008, 345(6):556-722. 10.1016/j.jfranklin.2008.01.005
Borek SE: An overview of through the wall surveillance for homeland security. Proceedings of the 34th Applied Imagery and Pattern Recognition Workshop: Multi-Modal Imaging, October 2005 42-47.
Hunt A: Image formation through walls using a distributed radar sensor array. Proceedings of the 32nd Applied Imagery Pattern Recognition Workshop, 2003 232-237.
Kim Y, Ling H: Human activity classification based on micro-Doppler signatures using a support vector machine. IEEE Transactions on Geoscience and Remote Sensing 2009, 47(5):1328-1337.
Mobasseri BG, Amin MG: A time-frequency classifier for human gait recognition. Optics and Photonics in Global Homeland Security V and Biometric Technology for Human Identification VI, April 2009, Orlando, Fla, USA, Proceedings of SPIE 7306:
Lyonnet B, Ioana C, Amin M: Human gait classification using micro-Doppler time-frequency signal representations. Proceedings of IEEE International Radar Conference (RADAR '10), May 2010, Washington, DC, USA
Tivive FHC, Bouzerdoum A, Phung SL, Iftekharuddin KM: Adaptive hierarchical architecture for visual recognition. Applied optics 2010, 49(10):B1-B8. 10.1364/AO.49.0000B1
Mitchell SJ, Silver RA: Shunting inhibition modulates neuronal gain during synaptic excitation. Neuron 2003, 38(3):433-445. 10.1016/S0896-6273(03)00200-9
Prescott SA, De Koninck Y: Gain control of firing rate by shunting inhibition: roles of synaptic noise and dendritic saturation. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(4):2076-2081. 10.1073/pnas.0337591100
Arulampalam G, Bouzerdoum A: A generalized feedforward neural network architecture for classification and regression. Neural Networks 2003, 16(5-6):561-568. 10.1016/S0893-6080(03)00116-3
Arulampalam G, Bouzerdoumn A: Training shunting inhibitory artificial neural networks as classifiers. Neural Network World 2000, 10(3):333-350.
Bouzerdoum A: Classification and function approximation using feed-forward shunting inhibitory artificial neural networks. Proceedings of the International Joint Conference on Neural Networks (IJCNN '00), July 2000 613-618.
Cheung HN, Bouzerdoum A, Newland W: Properties of shunting inhibitory cellular neural networks for colour image enhancements. Proceedings of the 6th International Conference on Neural Information Processing, 1999 3: 1219-1223.
Hammadou T, Bouzerdoum A: Novel image enhancement technique using shunting inhibitory cellular neural networks. IEEE Transactions on Consumer Electronics 2001, 47(4):934-940. 10.1109/30.982811
Bamberger RH, Smith MJT: A filter bank for the directional decomposition of images: theory and design. IEEE Transactions on Signal Processing 1992, 40(4):882-893. 10.1109/78.127960
Park S-I, Smith MJT, Mersereau RM: Improved structures of maximally decimated directional filter banks for spatial image analysis. IEEE Transactions on Image Processing 2004, 13(11):1424-1431. 10.1109/TIP.2004.836186
Nguyen TT, Oraintara S: A class of multiresolution directional filter banks. IEEE Transactions on Signal Processing 2007, 55(3):949-961.
Folsom TC, Pinter RB: Primitive features by steering, quadrature, and scale. IEEE Transactions on Pattern Analysis and Machine Intelligence 1998, 20(11):1161-1173. 10.1109/34.730552
Bovik AC, Clark M, Geisler WS: Multichannel texture analysis using localized spatial filters. IEEE Transactions on Pattern Analysis and Machine Intelligence 1990, 12(1):55-73. 10.1109/34.41384
Hagan MH, Menhaj MB: Training feedforward networks with the Marquardt algorithm. IEEE Transactions on Neural Networks 1994, 5(6):989-993. 10.1109/72.329697
Tivive FHC, Bouzerdoum A: Efficient training algorithms for a class of shunting inhibitory convolutional neural networks. IEEE Transactions on Neural Networks 2005, 16(3):541-556. 10.1109/TNN.2005.845144
Tivive FHC, Bouzerdoum A: A gender recognition system using shunting inhibitory convolutional neural networks. Proceedings of the International Joint Conference on Neural Networks (IJCNN '06), July 2006 5336-5341.
Tivive FHC, Bouzerdoum A: A hierarchical learning network for face detection with in-plane rotation. Neurocomputing 2008, 71(16–18):3253-3263.
Chang C-C, Lin C-J: LIBSVM: a library for support vector machines. 2001, http://www.csie.ntu.edu.tw/~cjlin/libsvm/
Acknowledgment
This work is supported in part by a grant from the Australian Research Council (ARC).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tivive, F.H.C., Bouzerdoum, A. & Amin, M.G. A Human Gait Classification Method Based on Radar Doppler Spectrograms. EURASIP J. Adv. Signal Process. 2010, 389716 (2010). https://doi.org/10.1155/2010/389716
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/389716












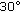 to the Axis of the Antenna
to the Axis of the Antenna