- Research Article
- Open access
- Published:
Estimation of Time-Varying Coherence and Its Application in Understanding Brain Functional Connectivity
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 390910 (2010)
Abstract
Time-varying coherence is a powerful tool for revealing functional dynamics between different regions in the brain. In this paper, we address ways of estimating evolutionary spectrum and coherence using the general Cohen's class distributions. We show that the intimate connection between the Cohen's class-based spectra and the evolutionary spectra defined on the locally stationary time series can be linked by the kernel functions of the Cohen's class distributions. The time-varying spectra and coherence are further generalized with the Stockwell transform, a multiscale time-frequency representation. The Stockwell measures can be studied in the framework of the Cohen's class distributions with a generalized frequency-dependent kernel function. A magnetoencephalography study using the Stockwell coherence reveals an interesting temporal interaction between contralateral and ipsilateral motor cortices under the multisource interference task.
1. Introduction
Previous studies in neuroscience have shown that cortico-cortical interactions play a crucial role in the performance of cognitive tasks. Understanding the underlying mechanism is useful not only for learning brain functionality, but also for guiding treatments of mental or behavioral diseases [1]. Since brain activities are characterized by multiple oscillators from different frequency bands [2], spectrum analysis has become a popular tool to noninvasively investigate the mechanisms of the brain functions [3]. Particularly, the coherence function, which estimates the linear relationship between two simultaneous time series as a function of frequency, is widely used to measure brain functional connectivity.
The traditional spectrum analysis, built on the theory of Fourier analysis, relies on the assumption that the underlying time series are stationary. However, the brain is a complex, nonstationary, massively interconnected dynamic system [2]. The functional interactions associated with cognitive and behavioral events are dynamic and transient. The temporal information, missed by Fourier analysis, needs to be addressed in order to better understand the dynamics of brain functionality. This leads to the development of time-varying spectrum.
In 1965, Priestley [4] defined the class of locally stationary time series and proposed the theory of evolutionary spectra to study their time-varying characteristics. His work links the theory of time series analysis to that of time-frequency analysis. That is, time-varying spectra can be estimated through a variety of time-frequency representations (TFRs) with different advantageous features. In 1966, Cohen [5] discovered that all the bilinear TFRs can be categorized as Cohen's class distributions whose properties are fully determined by their corresponding kernel functions. Specific Cohen's class distribution functions have been directly used to estimate evolutionary spectra in the past [6, 7]. However, there is no explicit explanation in the literature about the general connection of the evolutionary spectrum and the Cohen's class representations. In Section 2.3, we present such a connection in the context of Priestley's definition of time-varying spectrum.
Following the development of wavelet theory [8] over the last two decades, transforms that provide the multiresolution TFRs have been receiving growing attention in the field of time-frequency analysis. This is because the multiscale resolution provided by wavelet transforms offers a more accurate description of the nonstationary characteristics of a signal. However, the time-scale distribution provided by the wavelet transform may not be straightforwardly converted to a distribution in time-frequency domain. The Stockwell transform (ST), proposed by geophysicists [9] in 1996, is a hybrid of the Gabor transform (GT) and wavelet transform. Utilizing a Gaussian frequency-localization window of frequency-dependent window width, the ST provides a time-frequency representation whose resolution varies inversely proportional to the frequency variable. The ST has gained popularity in the signal processing community because of its easy interpretation and fast computation [10–12].
In this paper, we establish a general framework to estimate time-varying spectra using the Cohen's class distribution functions and apply it for a magnetoencephalography (MEG) study using the ST, a particular Cohen's class distribution. More specifically, the main contributions of this paper are the following. First, we revisit the definition of locally stationary time series to understand the desirable characteristics to define the time-varying spectra. We then show that the time-varying spectrum defined by the Cohen's class distributions coincides with the definition of the locally stationary time series. Second, we propose a new time-varying spectrum based on the ST. As a bilinear TFR, the spectrogram of the ST can be studied as an extended Cohen's class distribution. We derive the kernel function of the ST-spectrogram that can be used to investigate the characteristics of ST-based time-varying spectra in a simple way. Third, we define the time-varying coherence function using the ST-spectrogram. The multiscale characteristic and the nonnegativity make the ST an effective tool to investigate the time-varying linear connection between two signals. The performance of the proposed ST-based measures is demonstrated using a pair of synthetic time series. The numerical comparison with measures defined on the GT-spectrogram is also presented. In the end, we apply the ST-based time-varying coherence to the MEG data. Our findings reveal interesting temporal interaction between contralateral and ipsilateral motor (MIc and MIi) cortices under the multisource interference task (MSIT).
2. Time-Varying Spectra on the Cohen's Class Distributions
2.1. Spectrum Analysis of Stationary Time Series: A Review
In statistics, the autocorrelation of a time series describes the correlation between values of the time series at two different time instants. Given a time series  , let
, let  and
and  denote the mean value and standard deviation of the series at time
denote the mean value and standard deviation of the series at time  , respectively. The autocorrelation between two time points
, respectively. The autocorrelation between two time points  and
and  is mathematically defined as
is mathematically defined as

where  indicates the conjugate operator, and
indicates the conjugate operator, and  is the expectation operator. The definition (1) shows an explicit dependence on the two time indices. However by changing variables
is the expectation operator. The definition (1) shows an explicit dependence on the two time indices. However by changing variables  and
and  , the autocorrelation function can also be expressed as a function of the middle time point
, the autocorrelation function can also be expressed as a function of the middle time point  and the time index difference
and the time index difference  , that is,
, that is,  . The class of wide-sense stationary time series, studied extensively in time series analysis, has constant mean value over time, and their autocorrelation functions depend only on the time index difference
. The class of wide-sense stationary time series, studied extensively in time series analysis, has constant mean value over time, and their autocorrelation functions depend only on the time index difference  ,
,

While the autocorrelation function characterizes the statistical features of a time series in the time domain, these features can be also studied in the spectral domain through the Fourier analysis under the stationary assumption. The power spectral density (PSD) function, a widely used spectral domain measure, is defined as the Fourier spectrum of the autocorrelation function, that is,

Since  is the total energy of
is the total energy of  , the PSD function is often interpreted as an energy distribution of a time series in the frequency domain, and it provides an adequate description of the spectral characteristic of a stationary time series.
, the PSD function is often interpreted as an energy distribution of a time series in the frequency domain, and it provides an adequate description of the spectral characteristic of a stationary time series.
Additionally, the PSD function can be alternatively defined using the spectral representation of time series, that is,

Here, the PSD is treated as the limit of a statistical average of the modulus square of the Fourier spectrum of a truncated time series with a truncated length  as
as  goes to infinity. The Wiener-Khintchine theorem [13] proves the equivalence of the two definitions (3) and (4) under the condition that the autocorrelation function decays fast enough such that
goes to infinity. The Wiener-Khintchine theorem [13] proves the equivalence of the two definitions (3) and (4) under the condition that the autocorrelation function decays fast enough such that

The estimation of the PSD function via (4) is called the periodogram method, a popular nonparametric approach that can utilize the Fast Fourier transform (FFT) to improve the computational efficiency.
When studying the interdependence of a pair of time series  and
and  , the cross correlation can be defined as
, the cross correlation can be defined as

The stationary condition generalized to the joint wide-sense stationarity requires the cross-correlation function to depend on the time index difference only, that is,  . Note that a pair of time series that are jointly stationary must also be individually stationary. Similar to the PSD, the cross-spectral density (CSD) function can be estimated as the Fourier spectrum of the cross-correlation function
. Note that a pair of time series that are jointly stationary must also be individually stationary. Similar to the PSD, the cross-spectral density (CSD) function can be estimated as the Fourier spectrum of the cross-correlation function

The CSD function measures the interdependence of two time series as a function of frequency which makes it important in many applications. In order to properly compare the strength of the interdependence among different pairs of time series, the normalized CSD function that is a scale-free measure of interdependence is often used. It is also called the coherence function, denoted as  and given by
and given by

The Schwartz inequality guarantees that  ranges between 0 and 1. The coherence function actually measures the linear interaction between any two time series in the frequency domain. More specifically, when noise is absent,
ranges between 0 and 1. The coherence function actually measures the linear interaction between any two time series in the frequency domain. More specifically, when noise is absent,  for any two linear dependent time series since they are the input and output of a linear system
for any two linear dependent time series since they are the input and output of a linear system  , and
, and  if the two time series are linearly independent.
if the two time series are linearly independent.
2.2. Local Stationarity
While the stationary time series have time-invariant statistical properties, in reality, the measured signals may exhibit some time-varying features due to their intrinsic generating mechanisms or the variations of the outside environment. Therefore, the stationarity assumption, a mathematical idealization, is valid only as approximations. The performance of the analysis tools developed for the stationary time series depends on how stationary the underlying signals are. Advanced statistical preprocessing techniques have been proposed to convert a nonstationary time series to be "more stationary", but they are unable to completely eliminate the nonstationarity. On the other hand, in many applications, nonstationary characteristics of a signal are of great interest. For example, in neural information processing, the brain functional activity associated with the complex cognitive and behavioral events are highly time-varying. Such dynamics provide useful insights into the brain functionality. Therefore, it is desirable to develop statistical descriptions for the nonstationary time series.
It is natural to extend the well-established theory of stationary time series to certain classes of nonstationary time series, such as the locally stationary time series. The spectral characteristics of the locally stationary time series are assumed to change continuously but slowly over time, implying the existence of an interval centered at each time instant in which the time series are approximately stationary. The concept of the locally stationary time series was first introduced by Silverman [14] in 1957, and the generalization of the Wiener-Khintchine theorem to this special class of time series has also been established at the same time. Priestley [4, 6] gave a more rigorous definition of local stationarity using the oscillatory process and established an evolutionary spectrum theory. Hedges and Suter [15, 16] considered numerical means of measuring local stationarity in a time- and frequency-domain, while Galleani, Cohen, and Suter [17, 18] obtained a criteria to define local stationarity using time-frequency distributions. Besides the evolutionary spectra, other time-varying spectra can be developed under the assumption of local stationarity. As shown below, an estimation of a time-varying spectrum can be derived from the autocorrelation function of the locally stationary time series.
More specifically, given a locally stationary time series  , at any time instant
, at any time instant  , there exists a local interval of length
, there exists a local interval of length  centered at
centered at  , such that its autocorrelation function at any two time instants
, such that its autocorrelation function at any two time instants  and
and  satisfying
satisfying  can be well approximated by
can be well approximated by

where  is the time index difference
is the time index difference  . Note that the autocorrelation function
. Note that the autocorrelation function  around time
around time  depends only on the time index difference
depends only on the time index difference  within the region
within the region  , and the length
, and the length  of the locally stationary interval may vary with respect to time instant
of the locally stationary interval may vary with respect to time instant  [19].
[19].
Figure 1 illustrates the definition of a locally stationary time series. Figure 1(a) shows two locally stationary neighborhoods of a time series at two specific time points  and
and  . It is simpler to view these regions in the coordinates of the center time location
. It is simpler to view these regions in the coordinates of the center time location  and the time index difference
and the time index difference  as shown in Figure 1(b). Figure 1(b) demonstrates that the locally stationary neighborhood at any time
as shown in Figure 1(b). Figure 1(b) demonstrates that the locally stationary neighborhood at any time  is rhombus centered at
is rhombus centered at  with its size determined by the length of the locally stationary interval. The long diagonal of length
with its size determined by the length of the locally stationary interval. The long diagonal of length  is along the
is along the  direction with length, and the short diagonal of length
direction with length, and the short diagonal of length  is along the
is along the  direction. The autocorrelation function defined within the shaded area is invariant along the
direction. The autocorrelation function defined within the shaded area is invariant along the  axis, since the stationary condition indicates the dependence of the index difference
axis, since the stationary condition indicates the dependence of the index difference  only for the autocorrelation function.
only for the autocorrelation function.
The locally spectral information can be approximated by combining the operations of averaging  along the
along the  direction and then applying Fourier transform along the
direction and then applying Fourier transform along the  direction within the locally stationary area. To avoid the sidelobe effect, a two-dimensional localization function
direction within the locally stationary area. To avoid the sidelobe effect, a two-dimensional localization function  can be used to better localize the information of the autocorrelation function in the neighborhood of time instant
can be used to better localize the information of the autocorrelation function in the neighborhood of time instant  . The time-varying spectrum is then estimated by
. The time-varying spectrum is then estimated by

where  is the Fourier operator with respect to the variable
is the Fourier operator with respect to the variable  , and
, and  is the convolution operator with respect to the variable
is the convolution operator with respect to the variable  . Equation (10) presents the basic idea of developing statistical measures that capture the time-varying spectral characteristics of a locally stationary time series.
. Equation (10) presents the basic idea of developing statistical measures that capture the time-varying spectral characteristics of a locally stationary time series.
With many choices of localization functions  , a time-varying spectrum defined by (10) is certainly not unique. For simplicity, the notation
, a time-varying spectrum defined by (10) is certainly not unique. For simplicity, the notation  is used again to represent the time variable
is used again to represent the time variable  in defining the time-varying spectrum. A different choice of the localization function produces a time-varying spectrum with different characteristics in the time-frequency domain. To preserve its physical meaning, the time-varying spectrum as a generalization of the PSD is considered as an energy decomposition over time and frequency. Therefore, it is desirable to have the following properties.
in defining the time-varying spectrum. A different choice of the localization function produces a time-varying spectrum with different characteristics in the time-frequency domain. To preserve its physical meaning, the time-varying spectrum as a generalization of the PSD is considered as an energy decomposition over time and frequency. Therefore, it is desirable to have the following properties.
-
(1)
The time-varying spectrum, as an energy density function, is expected to be nonnegative, that is,
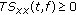 .
. -
(2)
The time-varying spectrum, as a decomposition of local energy over frequency, is expected to satisfy the time marginal condition, that is,
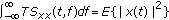 .
.
2.3. Time-Varying Spectra Estimated by the Cohen's Class Distributions
In this section, we extend the concepts in the FT-based spectral analysis to the time-frequency domain via the Cohen's class distributions for locally stationary time series. We also show that estimation of time-varying spectrum via the Cohen's class distributions is naturally coincided with (10).
Perhaps one of the most well-known Cohen's class distributions is the spectrogram given by the short-time Fourier transform (STFT). The STFT reveals the local features of a signal by applying the Fourier transform to the signal localized by a window function  that translates over time. Mathematically, the STFT is defined as
that translates over time. Mathematically, the STFT is defined as

The STFT with a Gaussian window function is also called the Gabor transform [20]. We can extend the Fourier-based definition of the PSD (4) to time-varying spectrum by replacing the Fourier transform with the STFT, namely,

Equation (12) is a bilinear TFR called the spectrogram. Since the STFT is considered as a localized Fourier transform, it is easy and intuitive to interpret the spectrogram. Hence, the spectrogram has become a popular tool to analyze locally stationary time series.
A more general form of a bilinear TFR, proposed by Cohen [5], can be mathematically expressed as

where  is a two-dimensional function called the kernel of the Cohen's class representation. Any bilinear transform can be obtained from (13) characterized by its kernel function. Different kernel functions can be designed such that the corresponding bilinear TFR has the desirable properties and also maintains the physical meaning of its energy distribution. For instance, the kernel of the spectrogram is
is a two-dimensional function called the kernel of the Cohen's class representation. Any bilinear transform can be obtained from (13) characterized by its kernel function. Different kernel functions can be designed such that the corresponding bilinear TFR has the desirable properties and also maintains the physical meaning of its energy distribution. For instance, the kernel of the spectrogram is

and the kernel of the Wigner-Ville distribution is simply  . Other commonly used Cohen's class distributions include Page distribution [21] and the Choi-Williams distribution [22].
. Other commonly used Cohen's class distributions include Page distribution [21] and the Choi-Williams distribution [22].
The importance of the Cohen's class representation is that it provides a general method to study the bilinear TFRs through a simple kernel function [7]. The characteristics of the TFRs are determined by the features of the kernel function. For example, the Cohen's class distributions satisfying the time marginal property, such as the Wigner-Ville distribution, require the corresponding kernel functions to satisfy

The kernel functions of the real-valued TFRs such as the Wigner-Ville distribution and the spectrogram have conjugate symmetry

With the Cohen's class distributions, we can easily derive a class of methods to estimate time-varying spectrum using the Cohen's class distributions by replacing the spectrogram in (12) by any bilinear TFR,

Here, the time-lag kernel  is the Fourier transform of the kernel function with respect to its first variable,
is the Fourier transform of the kernel function with respect to its first variable,

For example, the time-lag kernel for the Gabor transform is

As we can see, estimation (17) of the time-varying spectrum using the Cohen's class distribution (17) is consistent with the general methodology (10) of estimating time-varying spectrum for the locally stationary time series.
Since the time-lag kernel  acts as a localization function in (10), we can also define a way to measure the size of the locally stationary areas defined by the bilinear TFRs. Considering the absolute value of the normalized time-lag kernel as a probability density function, the center of the locally stationary area can be measured by the first moment, and the length of the locally stationary area can be estimated by the second moment. If the kernel has a single peak, the full-width half maximum (FWHM) of the kernel can also be used to estimate the size of the locally stationary area.
acts as a localization function in (10), we can also define a way to measure the size of the locally stationary areas defined by the bilinear TFRs. Considering the absolute value of the normalized time-lag kernel as a probability density function, the center of the locally stationary area can be measured by the first moment, and the length of the locally stationary area can be estimated by the second moment. If the kernel has a single peak, the full-width half maximum (FWHM) of the kernel can also be used to estimate the size of the locally stationary area.
However, not all Cohen's class distributions are suitable for estimating time-varying spectrum, especially for time-varying coherence. As energy distributions, nonnegative-valued bilinear distributions are desirable in spectral analysis. Negative values of the distribution may introduce difficulties in interpreting the time-vary spectrum and interactions between time series. As stated by Wigner [23], a bilinear distribution cannot satisfy the nonnegativity and the time marginal property simultaneously. Therefore, we focus on only the nonnegative-valued Cohen's class distributions.
The main limitation of the spectrogram is its fixed time and frequency resolution. In other words, the locally stationary region at any time has the same shape and size. However most signals in real applications have long durations of low-frequency components and short durations of high-frequency content. Hence, a time-lag kernel with frequency-dependent resolution is preferable so that local spectral information can be more accurately captured. In the next section, we will show that the spectrogram defined by the Stockwell transform is a nonnegative Cohen's class distribution, and the width of its corresponding kernel depends on the frequency variable. It thus provides a good estimate of the time-varying spectrum.
3. Time-Varying Spectra Estimated by the Stockwell Transform
The Stockwell transform, proposed by Stockwell in 1996 [9], is a hybrid of the Gabor transform and the wavelet transform. It provides a multiscale time-frequency representation of a signal. Specifically, the ST of a signal  with respect to a window function
with respect to a window function  is defined by
is defined by

or equivalently,

Here,  is the Fourier representation of
is the Fourier representation of  . Without loss of generality, we assume that
. Without loss of generality, we assume that  . In (20), the window function is scaled by
. In (20), the window function is scaled by  , and thus the ST provides frequency-dependent resolution in the time-frequency domain. The second definition (21) leads to fast computation of the ST by utilizing the fast Fourier transform. Furthermore, the ST is closely related to the classic Fourier transform since
, and thus the ST provides frequency-dependent resolution in the time-frequency domain. The second definition (21) leads to fast computation of the ST by utilizing the fast Fourier transform. Furthermore, the ST is closely related to the classic Fourier transform since

Therefore, the ST has become popular in many applications.
Similarly, we can estimate time-varying spectrum using the ST, that is,

The term inside  is the bilinear spectrogram of the ST. In fact, the ST-spectrogram belongs to the Cohen's class as shown in Theorem 1.
is the bilinear spectrogram of the ST. In fact, the ST-spectrogram belongs to the Cohen's class as shown in Theorem 1.
Theorem 1 (kernel of the ST-spectrogram).
Let  be a window function satisfying
be a window function satisfying  . For any signal
. For any signal  , the spectrogram of the ST with a window function
, the spectrogram of the ST with a window function  can be expressed by the extended Cohen's class representation
can be expressed by the extended Cohen's class representation

with the kernel function

or the time-lag kernel function

The proof can be found in the Appendix. Because the window width of the ST is frequency dependent, the corresponding kernel functions also depend on frequency.
The time-lag kernel function in Theorem 1 can help us understand the locally stationary areas defined by the ST-spectrogram. For example, the window function of the ST originally proposed by Stockwell [9] is a Gaussian function, that is,  . This is because the Gaussian function provides an optimal joint time-frequency resolution. The corresponding kernel function and the time-lag kernel function can be derived from Theorem 1
. This is because the Gaussian function provides an optimal joint time-frequency resolution. The corresponding kernel function and the time-lag kernel function can be derived from Theorem 1

Note that the time-lag kernel function is the product of two single-variable Gaussian functions

where one is scaled by  and the other by
and the other by  . We can measure the FWHM of the Gaussians as an approximation to the size of the time-lag kernels. Figures 2(a) and 2(b) illustrate the surface of time-lag functions at the location of half maximum for the GT- and ST-spectrograms, respectively. The locally stationary areas are frequency-invariant for the GT-spectrogram. On the contrary, the locally stationary area defined by the ST-spectrogram changes with respect to frequency: wide stationary area is applied to capture low-frequency information of the autocorrelation function, and a narrow stationary area is used to localize high-frequency components. Therefore, the multiscale time-varying spectrogram provides a robust and accurate description of the time-varying spectral information of a locally stationary time series.
. We can measure the FWHM of the Gaussians as an approximation to the size of the time-lag kernels. Figures 2(a) and 2(b) illustrate the surface of time-lag functions at the location of half maximum for the GT- and ST-spectrograms, respectively. The locally stationary areas are frequency-invariant for the GT-spectrogram. On the contrary, the locally stationary area defined by the ST-spectrogram changes with respect to frequency: wide stationary area is applied to capture low-frequency information of the autocorrelation function, and a narrow stationary area is used to localize high-frequency components. Therefore, the multiscale time-varying spectrogram provides a robust and accurate description of the time-varying spectral information of a locally stationary time series.
4. Time-Varying Coherence Estimated by the Stockwell Transform
In many applications, interdependence between two time series changes over time. It is necessary to have statistical measures such as time-varying coherence that can reveal such a dynamic relation. In this section, we define a time-varying coherence function for locally stationary time series by extending the Fourier-based coherence function to the time-frequency plane.
The generalization of time-varying coherence using the Cohen's class distributions follows straightforwardly the time-varying spectrum. The time-varying cross spectrum can be defined with the Cohen's class distributions by replacing the autocorrelation function in (17) with the cross-correlation function. Based on the representation of the Cohen's class, the time-varying cross spectra at each time instant can be interpreted as the spectral representation of the local cross-correlation function, which measures the linear interaction between the underlying two time series at this time instant. Similarly, the time-varying coherence function is defined as the normalization of the time-varying cross spectrum.
The time-varying coherence certainly inherits the characteristics of the time-varying spectra. Therefore, the multiscale characteristic of the ST-spectrogram makes it an effective tool to study the time-varying coherence. The ST cross spectrum and coherence can be defined as follows:

As a scale-free measure, the value of the time-varying coherence is expected to range from 0 to 1. Theorem 2 indicates that such property holds for the ST-based coherence.
Theorem 2 (range of ST coherence).
Let the window function  and satisfy
and satisfy  . For any two signals
. For any two signals  , the following inequality holds for the ST,
, the following inequality holds for the ST,

The proof follows directly the Schwartz inequality. Hence,  . Note that the spectrogram defined by the STFT also satisfies this inequality. However, for the Cohen's class distributions with negative values, their corresponding time-varying coherence functions do not hold this inequality. As a result, most of bilinear TFRs are not suitable to study the time-varying linear interdependence of time series.
. Note that the spectrogram defined by the STFT also satisfies this inequality. However, for the Cohen's class distributions with negative values, their corresponding time-varying coherence functions do not hold this inequality. As a result, most of bilinear TFRs are not suitable to study the time-varying linear interdependence of time series.
Besides the ST, the wavelet transforms also provide a multiscale resolution. Therefore, they can be applied to define the time-varying spectrum and coherence. The differences between the Stockwell approach and the wavelet approach have been investigated recently in [24].
5. Numerical Simulations
To demonstrate the performance of the ST-spectrogram in studying the time-varying characteristic of time series, we estimate the time-varying spectra and coherence of a pair of synthetic nonstationary time series using both the GT- and the ST-spectrogram with the Gaussian window. The two nonstationary time series are constructed as the follows:

where  are independent Gaussian noise with zero mean and identical variance. Note that both signals consist of the same chirp signal whose frequency linearly increases from 10 Hz to 20 Hz, and two constant frequency components (40 Hz and 80 Hz) occurred at different time periods. We generate two hundred trials of data using the Monte Carlo simulations. The sampling rate is 1000 Hz and the total sampling duration is 1 s. The time-varying spectra and the time-varying coherence are estimated using both the GT- and the ST-spectrograms.
are independent Gaussian noise with zero mean and identical variance. Note that both signals consist of the same chirp signal whose frequency linearly increases from 10 Hz to 20 Hz, and two constant frequency components (40 Hz and 80 Hz) occurred at different time periods. We generate two hundred trials of data using the Monte Carlo simulations. The sampling rate is 1000 Hz and the total sampling duration is 1 s. The time-varying spectra and the time-varying coherence are estimated using both the GT- and the ST-spectrograms.
In Figure 3, the first column is the time-varying spectra of  the second column is the time-varying spectra of
the second column is the time-varying spectra of  ; and the third column is the coherence functions of
; and the third column is the coherence functions of  and
and  . Figures 3(a)–3(c) are the results obtained by the GT-spectrogram with a narrower Gaussian window (
. Figures 3(a)–3(c) are the results obtained by the GT-spectrogram with a narrower Gaussian window ( s). The narrower time window yields a good time resolution but a poorer frequency resolution. On the contrary, Figures 3(d)–3(f) show the GT-based results with a wider Gaussian window (
s). The narrower time window yields a good time resolution but a poorer frequency resolution. On the contrary, Figures 3(d)–3(f) show the GT-based results with a wider Gaussian window ( s), where the spectra and the coherence function have a poorer time resolution but a good frequency resolution. Figures 3(g)–3(i) are the results obtained from the ST-spectrogram. The frequency-dependent resolution produces a good time resolution at high frequencies and a good frequency resolution at low frequencies.
s), where the spectra and the coherence function have a poorer time resolution but a good frequency resolution. Figures 3(g)–3(i) are the results obtained from the ST-spectrogram. The frequency-dependent resolution produces a good time resolution at high frequencies and a good frequency resolution at low frequencies.
Time-varying spectra of s1 and s2 and their coherence obtained from (a)–(c) the GT-spectrogram with the standard derivation of the Gaussian window σ = 0.05 s, (d)–(f) the GT-spectrogram with the standard derivation of the Gaussian window σ = 0.02 s, and (g)–(i) the ST-spectrogram. (a) Spectrum (Gabor) of s1 with scale σ = 0.05 s (b)Spectrum (Gabor) of s2 with scale σ = 0.05 s (c)Coherence (Gabor) with scale σ = 0.05 s (d)Spectrum (Gabor) of s1 with scale σ = 0.2 s (e)Spectrum (Gabor) of s2 with scale σ = 0.2 s (f)Coherence (Gabor) with scale σ = 0.2 s (g)Spectrum (Stockwell) of s1 (h)Spectrum (Stockwell) of s2Coherence (Stockwell)
Since  and
and  are related only by the chirp signal, their coherence should happen only at the location of the chirp signal. Due to the limitations of the windowing technique, the temporal occurrences of the two constant frequency components overlap in all of the estimated time-varying spectra, causing false coherence beyond 20 Hz around 0.5 s. The frequency-dependent resolution of the ST-spectrogram produces an overall better picture about the coherence of these two signals.
are related only by the chirp signal, their coherence should happen only at the location of the chirp signal. Due to the limitations of the windowing technique, the temporal occurrences of the two constant frequency components overlap in all of the estimated time-varying spectra, causing false coherence beyond 20 Hz around 0.5 s. The frequency-dependent resolution of the ST-spectrogram produces an overall better picture about the coherence of these two signals.
6. An Application in Studying the Brain Functional Connectivity
We now apply the time-varying coherence based on the Stockwell transform to study functional connectivity between the contralateral and ipsilateral motor cortices when subjects performed the Multisource Interference Task [25] using their right hands. The MSIT combines multiple dimensions of cognitive interference in a single task, which can be used to investigate mental or behavioral diseases such as Attention Deficit Hyperactivity Disorder (ADHD) in clinical studies [1]; see Figure 4 for details of the MSIT. Fifty interference trials were recorded for two right-handed participants (SB and DM, represented by their initials). One hundred fifty-one channel whole-head MEG (sample rate = 625 Hz) was recorded continuously for 400 seconds. Time zero is represented as a press of the button. The signals at contralateral and ipsilateral motor cortices were extracted using the beamformer technique [26] and filtered with a low-pass filter (1–30 Hz). Several preprocessing steps have been applied to the data, including temporal normalization to give the data equal weight and ensemble mean subtraction to remove first-order nonstationarity [27].
For each subject, we calculate the time-varying spectrum based on the ST-spectrogram with the preprocessed data −1–1.5 s. To investigate the statistical significance of time-varying coherence measure, we apply the bootstrap method [28] with 500 resamples and significance level  . Since the Stockwell time-frequency representation often contains artifacts at the two ends of a time series due to circular Fourier spectrum shifting in the implementation, we examine the significant ST-based time-varying coherence only during the time period −0.6–0 s. Another reason why we are particularly interested in this period is that the reaction time of those two subjects is approximately 0.6 s, which suggests that subjects are processing their cognitive tasks within the time interval.
. Since the Stockwell time-frequency representation often contains artifacts at the two ends of a time series due to circular Fourier spectrum shifting in the implementation, we examine the significant ST-based time-varying coherence only during the time period −0.6–0 s. Another reason why we are particularly interested in this period is that the reaction time of those two subjects is approximately 0.6 s, which suggests that subjects are processing their cognitive tasks within the time interval.
The ST-based coherence indicates the functional connection between the MIc and MIi under the MIST. Figure 5 shows that the significant connection happens mainly around frequency bands of 10–14 Hz and 25 Hz. For the 10–14 Hz frequency band, our results are consistent with the results found in [29], where activities of MIi and predominantly corticocortical coupling around 8–12 Hz have been observed under the unimanual auditorily paced finger-tapping task. The connection around 25 Hz in this experiment is new and needs to be further investigated. The common limitation of studying brain signals is the unavailability of large amounts of data. Statistical measurements with few samples may combine with artifacts. In order to improve accuracy, grand average results among more subjects need to be studied and will be further considered in the future.
7. Conclusions
In this paper, we investigate the estimation of the time-varying spectrum and the time-varying coherence for the locally stationary time series using the Cohen's class distributions. We have shown that the estimation of time-varying spectrum via Cohen's class distributions (17) is naturally coincided with the definition of the locally stationary time series (10). In addition, the availability of the Cohen's class representation provides a new perspective into the characteristics of time-varying spectrum via studying the properties of the corresponding kernel. However, to maintain physical meaningness in time-varying spectrum and coherence, only nonnegative Cohen's class distribution is preferable. To more accurately capture the local features of a locally stationary time series, a distribution with a multiscale resolution is desirable although most of the standard Cohen's class distribution have fixed resolution. Therefore, we propose new time-varying measures based on the spectrogram of the Stockwell transform, a hybrid of the Short-time Fourier transform and the wavelet transform. We prove that as a bilinear TFR, the ST-spectrogram is a Cohen's class distributions with a frequency-dependent kernel. The multiscale analysis and the nonnegativity feature make the ST an effective approach to investigate the time-varying characteristics of the spectrum and the interaction of locally stationary time series. We successfully apply the ST-based time-varying coherence to study the brain functional connectivity in an MEG study.
References
Bush G, Spencer TJ, Holmes J, Shin LM, Valera EM, Seidman LJ, Makris N, Surman C, Aleardi M, Mick E, Biederman J: Functional magnetic resonance imaging of methylphenidate and placebo in attention-deficit/hyperactivity disorder during the multi-source interference task. Archives of General Psychiatry 2008, 65(1):102-114. 10.1001/archgenpsychiatry.2007.16
Buzsaki G: Rhythms of the Brain. Oxford University Press, New York, NY, USA; 2006.
Marple SL Jr.: Digital Spectral Analysis with Applications. Prentice Hall, Englewood Cliffs, NJ, USA; 1987.
Priestley MB: Evolutionary spectra and non-stationary processess. Journal of the Royal Statistical Society: Series B 1965, 27(2):204-237.
Cohen L: Time-Frequency Analysis. Prentice Hall, Englewood Cliffs, NJ, USA; 1995.
Priestley MB: Spectral Analysis and Time Series. Volume 2. Academic Press, New York, NY, USA; 1981.
Adak S: Time-dependent spectral analysis of nonstationary time series, Ph.D. thesis. Stanford Univerisity; 1996.
Daubechies I: Ten Lectures on Wavelets. SIAM, Philadelphia, Pa, USA; 1992.
Stockwell RG, Mansinha L, Lowe RP: Localization of the complex spectrum: the S transform. IEEE Transactions on Signal Processing 1996, 44(4):998-1001. 10.1109/78.492555
Zhu H, Goodyear BG, Lauzon ML, Brown RA, Mager GS, Law AG, Mansinha L, Mitchell JR: A new local multiscale Fourier analysis for medical imaging. Medical Physics 2003, 30(6):1134-1141. 10.1118/1.1576931
Goodyear BG, Zhu H, Brown RA, Mitchell JR: Removal of phase artifacts from fMRI data using a Stockwell transform filter improves brain activity detection. Magnetic Resonance in Medicine 2004, 51(1):16-21. 10.1002/mrm.10681
Pinnegar CR: Polarization analysis and polarization filtering of three-component signals with the time-frequency S transform. Geophysical Journal International 2006, 165(2):596-606. 10.1111/j.1365-246X.2006.02937.x
Yaglom AM: An Introduction to the Theory of Stationary Random Functions. Prentice Hall, Englewood Cliffs, NJ, USA; 1962.
Silverman RA: Locally Stationary Random Processes. IRE Transactions on Information Theory 1957, 3: 182-187. 10.1109/TIT.1957.1057413
Hedges RA, Suter BW: Improved radon-transform-based method to quantify local stationarity. In Advanced Signal Processing Algorithms, Architectures, and Implementations X, August 2000, San Diego, Calif, USA, Proceedings of SPIE Edited by: Luk FT. 4116: 17-24.
Hedges RA, Suter BW: Numerical spread: quantifying local stationarity. Digital Signal Processing 2002, 12(4):628-643. 10.1006/dspr.2002.0428
Galleani L, Cohen L, Suter B: Locally stationary noise and random processes. Proceedings of the 5th International Workshop on Information Optics, June 2006, Toledo, Spain 514-519.
Galleani L, Cohen L, Suter B: Local stationarity and time-frequency distributions. Advanced Signal Processing Algorithms, Architectures, and Implementations XVI, August 2006, San Diego, Calif, USA, Proceedings of SPIE 6313:
Mallat S, Papanicolaou G, Zhang Z: Adaptive covariance estimation of locally stationary processes. Annals of Statistics 1998, 26(1):1-47.
Gabor D: Theory of communication. Journal I.E.E. 1946, 93: 429-457.
Page CH: Instantaneous power spectra. Journal of Applied Physics 1952, 23(1):103-106. 10.1063/1.1701949
Choi H, Williams WJ: Improved time-frequency representation of multicomponent signals using exponential kernels. IEEE Transactions on Acoustics, Speech, and Signal Processing 1989, 37(6):862-871. 10.1109/ASSP.1989.28057
Wigner E: On the quantum correction for thermodynamic equilibrium. Physical Review 1932, 40(5):749-759. 10.1103/PhysRev.40.749
Liu C, Gaetz W, Zhu H: The Stockwell transform in studying the dynamics of brain functions. Proceedings of the International Workshop Pseudo-Differential Operators: Complex Analysis and Partial Differential Equations, August 2008 277-291.
Bush G, Shin LM: The multi-source interference task: an fMRI task that reliably activates the cingulo-frontal-parietal cognitive/attention network. Nature Protocols 2006, 1(1):308-313. 10.1038/nprot.2006.48
Cheyne D, Bostan AC, Gaetz W, Pang EW: Event-related beamforming: a robust method for presurgical functional mapping using MEG. Clinical Neurophysiology 2007, 118(8):1691-1704. 10.1016/j.clinph.2007.05.064
Ding M, Bressler SL, Yang W, Liang H: Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling: data preprocessing, model validation, and variability assessment. Biological Cybernetics 2000, 83(1):35-45. 10.1007/s004229900137
Efron B: The Jackknife, the Bootstrap, and other Resampling Plans. SIAM, Philadelphia, Pa, USA; 1987.
Pollok B, Gross J, Müller K, Aschersleben G, Schnitzler A: The cerebral oscillatory network associated with auditorily paced finger movements. NeuroImage 2005, 24(3):646-655. 10.1016/j.neuroimage.2004.10.009
Acknowledgments
The authors would like to thank the financial support from Natural Sciences and Engineering Research Council of Canada and Ontario Centres of Excellence.
Author information
Authors and Affiliations
Corresponding author
Appendix
A. Proof of Theorem 1
Consider the spectrogram of the Stockwell transform


Then, the kernel function can be obtained as


The interchange of the order of integrals is guaranteed by the Fubini's theorem since the window function  is bounded and
is bounded and  .
.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, C., Gaetz, W. & Zhu, H. Estimation of Time-Varying Coherence and Its Application in Understanding Brain Functional Connectivity. EURASIP J. Adv. Signal Process. 2010, 390910 (2010). https://doi.org/10.1155/2010/390910
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/390910

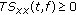 .
.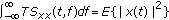 .
.


