- Research Article
- Open access
- Published:
Image Variational Denoising Using Gradient Fidelity on Curvelet Shrinkage
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 398410 (2010)
Abstract
A new variational image model is presented for image restoration using a combination of the curvelet shrinkage method and the total variation (TV) functional. In order to suppress the staircasing effect and curvelet-like artifacts, we use the multiscale curvelet shrinkage to compute an initial estimated image, and then we propose a new gradient fidelity term, which is designed to force the gradients of desired image to be close to the curvelet approximation gradients. Then, we introduce the Euler-Lagrange equation and make an investigation on the mathematical properties. To improve the ability of preserving the details of edges and texture, the spatial-varying parameters are adaptively estimated in the iterative process of the gradient descent flow algorithm. Numerical experiments demonstrate that our proposed method has good performance in alleviating both the staircasing effect and curvelet-like artifacts, while preserving fine details.
1. Introduction
Image denoising is a very important preprocessing in many computer vision tasks. The tools for attracting this problem come from computational harmonic analysis (CHA), variational approaches, and partial differential equations (PDEs) [1]. The major concern in these image denoising models is to preserve important image features, such as edges and texture, while removing noise.
In the direction of multi-scale geometrical analysis (MGA), the shrinkage algorithms based on the CHA tools, such as contourlets [2] and curvelets [3–5], are very important in image denoising because they are simple and have efficient computational complexity and promising properties for singularity analysis. Therefore, the pseudo-Gibbs artifacts caused by the shrinkage methods based on Fourier transform and wavelets attempt to be overcame by the methods based on MGA at least partially. However, there are still some curve-like artifacts in MGA-based shrinkage methods [6].
Algorithms designed by variatinal and PDE models are free from the above lacks of MGA but cost heavy computational burden that is not suitable for time critical application. In addition, the PDE-based algorithms tend to produce a staircasing effect [7], although they can achieve a good trade-off between noise removal and edge preservation. For instance, the total variation (TV) minimizing [8] method has some undesirable drawbacks such as the staircasing effect and loss of texture, although it can reduce pseudo-Gibbs oscillations effectively. Similar problem can be found in many other nonlinear diffusion models such as the Perona-Malik model [9] and the mean curvature motion model [10]. In this paper, we will focus on the hybrid variational denoising method. Specificity, we will emphasis on the improvement on the TV model, and we will propose a novel gradient fidelity term based on the curvelet shrinkage algorithm.
1.1. Related Works and Analysis
To begin with, we will review some related works of the variational methods. To cope with the ill-posed nature of denoising, the variational methods often use regularization technique. Let  denote the observed raw image data and
denote the observed raw image data and  is the original good image; then the regularization functional-based denoising is given by
is the original good image; then the regularization functional-based denoising is given by

where the first term  is the image fidelity term, which penalizes the inconsistency between the under-estimated recovery image and the acquired noisy image, while the second term
is the image fidelity term, which penalizes the inconsistency between the under-estimated recovery image and the acquired noisy image, while the second term  is the regularization term which imposes some priori constraints on the original image and to a great degree determines the quality of the recovery image, and
is the regularization term which imposes some priori constraints on the original image and to a great degree determines the quality of the recovery image, and  is the regularization parameter which balances trade-off between the image fidelity term
is the regularization parameter which balances trade-off between the image fidelity term  and the regularization term
and the regularization term  .
.
A classical model is the minimizing total variational (TV) functional [8]. The TV model seeks the minimal energy of an energy functional comprised of the TV norm of image  and the fidelity of this image to the noisy image
and the fidelity of this image to the noisy image  :
:

Here,  denotes the image domain and
denotes the image domain and  is the space of functions of
is the space of functions of  such that the TV norm is
such that the TV norm is  . The gradient descent evolution equation is
. The gradient descent evolution equation is

In this formulation,  can be considered as a Lagrange multiplier, computed by
can be considered as a Lagrange multiplier, computed by

Although the TV model can reduce oscillations and regularize the geometry of level sets without penalizing discontinuities, it possesses some properties which may be undesirable under some circumstances [11], such as staircasing and loss of texture (see Figures 1(a)–1(c)).
Currently, there are three approaches which can partially overcome these drawbacks. One approach to preventing staircasing is to introduce higher-order derivatives into the energy. In [12], an image  is decomposed into two parts:
is decomposed into two parts:  . The
. The  component is measured using the total variation norm, while the second component
component is measured using the total variation norm, while the second component  is measured using a higher-order norm. More precisely, one solves the following variational problem that now involves two unknowns:
is measured using a higher-order norm. More precisely, one solves the following variational problem that now involves two unknowns:

Here  could be some higher-order norm, for example,
could be some higher-order norm, for example,  . More complex higher-order norms were brought to variational method in order to alleviate the staircasing effect [13].
. More complex higher-order norms were brought to variational method in order to alleviate the staircasing effect [13].
The second approach overcoming the staircasing effect is to adopt the new data fidelity term. Gilboa et al. proposed an adaptive fidelity term to better preserve fine-scale features [14]. Zhu and Xia in [7] introduced the gradient fidelity term defined by

where  is the Gaussian kernel with scale
is the Gaussian kernel with scale  , and the symbol "
, and the symbol " " denotes the convolution operator. Their studies show that this gradient fidelity term can alleviate the staircasing effect. However, classical Gaussian filtering technique is the uniform smoothing in all direction of images and fine details are easily destroyed with these filters. Hence, the gradient of smoothed image is unreliable near the edges, and the gradient fidelity cannot preserve the gradient and thereby image edges.
" denotes the convolution operator. Their studies show that this gradient fidelity term can alleviate the staircasing effect. However, classical Gaussian filtering technique is the uniform smoothing in all direction of images and fine details are easily destroyed with these filters. Hence, the gradient of smoothed image is unreliable near the edges, and the gradient fidelity cannot preserve the gradient and thereby image edges.
The third approach is the combination of the variational model and the MGA tools. In [14], the TV model has been combined with wavelet to reduce the pseudo-Gibbs artifacts resulted from wavelet shrinkage [15]. Nonlinear diffusion has been combined with wavelet shrinkage to improve the rotation invariance [16]. The author in [17] presented a hybrid denoising methods in which the complex ridgelet shrinkage was combined with total variation minimization [6]. From their reports, the combination of MGA and PDE methods can improve the visual quality of the restored image and provides a good way to take full advantages of both methods.
1.2. Main Contribution and Paper's Organization
In this paper, we add a new gradient fidelity term to the TV model to some second-order nonlinear diffusion PDEs for avoiding the staircasing effect and curvelet-like artifacts. This new gradient fidelity term provides a good mechanism to combine curvelet shrinkage algorithm and the TV regularization.
This paper is organized as follows. In Section 2, we introduce the curvelet transform. In Section 3, we propose a new hybrid model for image smoothing. In this model, we have two main contributions. We propose a new hybrid fidelity term, in which the gradient of multi-scale curvelet shrinkage image is used as a feature fidelity term in order to suppress the staircasing effect and curvelet-like artifacts. Secondly, we propose an adaptive gradient descent flow algorithm, in which the spatial-varying parameters are adaptively estimated to improve the ability of preserving the details of edges and texture of the desired image. In Section 4, we give numerical experiments and analysis.
The pipeline of our proposed method is illustrated in Figure 2. There are three core modules in our method. In the first module, we apply the curvelet shrinkage algorithm to obtain a good initial restored image  . The second module is the minimizing TV with the new gradient fidelity, and this module is a global optimizing process which is guided by our proposed general objective functional. The third one is the parameters adjustment module, which provides an adaptive process to compute the value for the system's parameters. The rationale behind the proposed method is that high visual quality image restoration scheme is expected to be a blind process to filter out noise, preserve the edge, and alleviate other artifacts.
. The second module is the minimizing TV with the new gradient fidelity, and this module is a global optimizing process which is guided by our proposed general objective functional. The third one is the parameters adjustment module, which provides an adaptive process to compute the value for the system's parameters. The rationale behind the proposed method is that high visual quality image restoration scheme is expected to be a blind process to filter out noise, preserve the edge, and alleviate other artifacts.
2. Curvelet Transform
In the next, we review the basic principles of curvelets which were originally proposed by Candès et al. in [5]. Let  and
and  be a pair of smooth, non-negative real-valued functions; here
be a pair of smooth, non-negative real-valued functions; here  is called "radial window" and
is called "radial window" and  is called "angular window". Both of them need to satisfy the admissibly conditions:
is called "angular window". Both of them need to satisfy the admissibly conditions:

Now, for each  , let the window
, let the window  in Fourier domain be given by
in Fourier domain be given by

where  is the integer part of
is the integer part of  and
and  denotes the polar coordinate; thus the support of
denotes the polar coordinate; thus the support of  is a polar "wedge" which is determined by "radial window" and "angular window". Let
is a polar "wedge" which is determined by "radial window" and "angular window". Let  be the Fourier transform of
be the Fourier transform of  , that is,
, that is,  . We may think of
. We may think of  as a "mother" curvelet in the sense that all curvelets at scale
as a "mother" curvelet in the sense that all curvelets at scale  are obtained by rotation and translations of
are obtained by rotation and translations of  . Let
. Let  be the rotation matrix by
be the rotation matrix by  radians and
radians and  its inverse, then curvelets are indexed by three parameters: a scale
its inverse, then curvelets are indexed by three parameters: a scale  an equispaced sequence of orientation
an equispaced sequence of orientation  , and the position
, and the position  . With these parameters, the curvelets are defined by
. With these parameters, the curvelets are defined by

A curvelet coefficient is then simply the inner product between an element  and a curvelet
and a curvelet  , that is,
, that is,

Let  be the collection of the triple index. The family of curvelet functions forms a tight frame of
be the collection of the triple index. The family of curvelet functions forms a tight frame of  . That means that each function
. That means that each function  has a representation:
has a representation:

where  denotes the
denotes the  -scalar product of
-scalar product of  and
and  . The coefficients
. The coefficients  are called coefficients of function
are called coefficients of function  . In this paper, we apply the second-generation curvelet transform, and the digital implementations can be outlined roughly as three steps [5]: apply 2D FFT, product with frequency windows, and apply 2D inverse FFT for each window. The forward and inverse curvelet transforms have the same computational cost of
. In this paper, we apply the second-generation curvelet transform, and the digital implementations can be outlined roughly as three steps [5]: apply 2D FFT, product with frequency windows, and apply 2D inverse FFT for each window. The forward and inverse curvelet transforms have the same computational cost of  for an
for an  data [11]. More details on curvelets and recent applications can be found in recent reviewer papers [3–6, 18, 19]. Figure 3 shows the elements of curvelets in comparison with wavelets. Note that the tensor-product 2D wavelets are not strictly isotropic but have three directions, while curvelets have almost arbitrary directional selectivity.
data [11]. More details on curvelets and recent applications can be found in recent reviewer papers [3–6, 18, 19]. Figure 3 shows the elements of curvelets in comparison with wavelets. Note that the tensor-product 2D wavelets are not strictly isotropic but have three directions, while curvelets have almost arbitrary directional selectivity.
3. Combination TV Minimization withGradient Fidelity on Curvelet Shrinkage
3.1. The Proposed Model
We start from the following assumed additive noise degradation model:

where  denotes the observed raw image data,
denotes the observed raw image data,  is the original good image, and
is the original good image, and  is additive measurement noise. The goal of image denoising is to recover
is additive measurement noise. The goal of image denoising is to recover  from the observed image data
from the observed image data  . The shrinkage algorithm on some multi-scale frame
. The shrinkage algorithm on some multi-scale frame  can be written as follows:
can be written as follows:

where  is the corresponding MGA operator, that is,
is the corresponding MGA operator, that is,  , for all
, for all  , and "
, and " " is a set of indices. The rational is that the noise
" is a set of indices. The rational is that the noise  is nearly Gaussian. The principles of the shrinkage estimators which estimate the frame coefficients
is nearly Gaussian. The principles of the shrinkage estimators which estimate the frame coefficients  from the observed coefficients
from the observed coefficients  have been discussed in different frameworks such as Bayesian and variational regularization [20, 21].
have been discussed in different frameworks such as Bayesian and variational regularization [20, 21].
Although traditional wavelets perform well only for representing point singularities, they become computationally inefficient for geometric features with line and surface singularities. To overcome this problem, we choose the curvelet as the tool of shrinkage algorithm. In general, the shrinkage operators are considered to be in the form of a symmetric function  ; thus the coefficients are estimated by
; thus the coefficients are estimated by

Let  denote the dual frame, and then a denoised image
denote the dual frame, and then a denoised image  is generated by the reconstruction algorithm:
is generated by the reconstruction algorithm:

Following the wavelet shrinkage idea which was proposed by Donoho and Johnstone [22], the curvelet shrinkage operators  can be taken as a soft thresholding function defined by a fixed threshold
can be taken as a soft thresholding function defined by a fixed threshold  , that is,
, that is,

or a hard shrinkage function

The major problem with wavelet shrinkage methods, as discussed, is that shrinking large coefficients entails an erosion of the spiky image features, while shrinking small coefficients towards zero yields Gibbs-like oscillation in the vicinity of edges and loss of texture. As a new MGA tool, Curvelet shrinkage can suppress this pseudo-Gibbs and preserve the image edge; however, some shapes of curve-like artifacts are generated (see Figure 4).
In order to suppress the staircasing effect and curvelet-like artifacts, we propose a new objective functional:

In the cost functional (18), the term  is called curvelet shrinkage-based gradient data fidelity term and is designed to force the gradient of
is called curvelet shrinkage-based gradient data fidelity term and is designed to force the gradient of  to be close to the gradient estimation
to be close to the gradient estimation  and to alleviate the staircase effect. And the parameters
and to alleviate the staircase effect. And the parameters  and
and  control the weights of each term. For the sake of simplicity for description, we always let
control the weights of each term. For the sake of simplicity for description, we always let  and
and  in the following sections.
in the following sections.
3.2. Basic Properties of Our Model
Let us denote

Then, the cost function is a new hybrid data fidelity term, and its corresponding Euler equation is

Proposition 1.
The Euler equation (20) equals to produce a new image whose Fourier transform is described as follows: if  , then
, then

Proof.
Apply Fourier transform to the Euler equation (20) and we will get

According to the differential properties of the Fourier transform

we have

If  , then we get
, then we get

where  and
and  are parameters in the frequency domain.
are parameters in the frequency domain.
Proposition 1 tells us that the Euler equation (20) equals to compute a new image whose Fourier frequency spectrum is the interpolation of  and
and  . The weight coefficients of
. The weight coefficients of  and
and  are
are  and
and  , respectively.
, respectively.
Proposition 2.
The energy functional  is convex.
is convex.
Proof.
For all  for all
for all  , on one hand we have the following conclusion:
, on one hand we have the following conclusion:

On the other hand, we have the following conclusion:

Then, we have

According to (26) and (28), we get the 
From Proposition 2, the convexity of the energy functional can guarantee the global optimizing and the existence of the unique solution, while Proposition 1 shows us that the solution has some special form in Fourier domain. Combining Propositions 1 and 2 together, we can remark that the unique solution of (19) is

Then, we can prove the following existence and uniqueness theorem.
Theorem 1.
Let  be a positive, bounded function with
be a positive, bounded function with  ; then the minimizing problem of energy functional
; then the minimizing problem of energy functional  in (18) admits a unique solution
in (18) admits a unique solution  satisfying
satisfying

Proof.
Using the lower semicontinuity and compactness of  and the convexity of
and the convexity of  , the proof can be made following the same procedure of [23, 24] (for detail, see appendix in [24]).
, the proof can be made following the same procedure of [23, 24] (for detail, see appendix in [24]).
3.3. Adaptive Parameters Estimation
For solving the minimizing energy functional  , it often transforms the optimizing problem into the Euler-Lagrange equation. Using the standard computation of Calculus of Variation of
, it often transforms the optimizing problem into the Euler-Lagrange equation. Using the standard computation of Calculus of Variation of  with respect to
with respect to  , we can get its Euler-Lagrange equation:
, we can get its Euler-Lagrange equation:

where  is the outward unit normal vector on the boundary
is the outward unit normal vector on the boundary  , and
, and  . For a convenient numerical simulation of (31), we apply the gradient descent flow and get the evolution equation:
. For a convenient numerical simulation of (31), we apply the gradient descent flow and get the evolution equation:

There are three parameters  involved in the iterative procedure. For the threshold parameter
involved in the iterative procedure. For the threshold parameter  in the curvelet coefficients shrinkage, the common one is to choose
in the curvelet coefficients shrinkage, the common one is to choose  , where
, where  denotes the standard deviation of Gaussian white noise. The Monte-Carlo simulations can calculate an approximation value
denotes the standard deviation of Gaussian white noise. The Monte-Carlo simulations can calculate an approximation value  of the individual variance. In our experiments, we use the following hard-thresholding rule for estimating the unknown curvelet coefficients:
of the individual variance. In our experiments, we use the following hard-thresholding rule for estimating the unknown curvelet coefficients:

Here, we actually chose a scale-dependent value for  : we have
: we have  for the first scale (the finest scale) and
for the first scale (the finest scale) and  for the others.
for the others.
For the parameters  and
and  , they are very important to balance trade-off between the image fidelity term and the regularization term. An important prior fact is that the Gaussian distributed noise has the following restriction condition:
, they are very important to balance trade-off between the image fidelity term and the regularization term. An important prior fact is that the Gaussian distributed noise has the following restriction condition:

Therefore, we merely multiply the first equation of (32) by  and integrate by parts over
and integrate by parts over  ; if the steady state has been reached, the left side of the first equation of (32) vanishes; thus we have
; if the steady state has been reached, the left side of the first equation of (32) vanishes; thus we have

Obviously, the above equation is not sufficient to estimate the values of  and
and  simultaneously. This implies that we should introduce another prior knowledge. Borrowing the idea of spatial varying data fidelity from Gilboa [14], we compute the parameter by the formula:
simultaneously. This implies that we should introduce another prior knowledge. Borrowing the idea of spatial varying data fidelity from Gilboa [14], we compute the parameter by the formula:

where  , and
, and  is the local power of the residue
is the local power of the residue  . The local power of the residue is given by
. The local power of the residue is given by

where  is a normalized and radially symmetric Gaussian Function window, and
is a normalized and radially symmetric Gaussian Function window, and  is the expected value. After we compute the value of
is the expected value. After we compute the value of  , we can estimate the value of
, we can estimate the value of  using (38), that is,
using (38), that is,

3.4. Description of Proposed Algorithm
To discretize equation (32), the finite difference scheme in [8] is used. Denote the space step by  and the time step by
and the time step by  . Thus we have
. Thus we have

where  and
and  is the regularized parameter chosen near 0.
is the regularized parameter chosen near 0.
The numerical algorithm for (32) is given in the following (the subscripts  are omitted):
are omitted):

with boundary conditions

for  . The parameters are chosen like this:
. The parameters are chosen like this:  , while the parameters
, while the parameters  are computed dynamically during the iterative process according to the formulae (33), (36), and (38).
are computed dynamically during the iterative process according to the formulae (33), (36), and (38).
In summary, according to the gradient descent flow and the discussion of parameters choice, we now present a sketch of the proposed algorithm (the pipeline is shown in Figure 2).
Initialization
 , Iterative-Steps
, Iterative-Steps
Curvelet Shrinkage.
-
(1)
Apply curvelet transform (the FDCT [5]) to noisy image
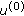 and obtain the discrete coefficients
and obtain the discrete coefficients 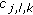 .
. -
(2)
Use robust method to estimate an approximation value
 , and then use the shrinkage operator in (33) to obtain the estimated coefficients
, and then use the shrinkage operator in (33) to obtain the estimated coefficients 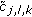 .
. -
(3)
Apply the inverse curvelet transform and obtain the initial restored image
 .
.
Iteration. While Iterative-Steps Do
Iterative-Steps Do
-
(1)
Compute
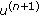 according to (40).
according to (40). -
(2)
Update the parameter
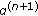 according to (36).
according to (36). -
(3)
Update the parameter
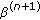 according to (38).
according to (38).
End Do Output:  .
.
3.5. Analysis of Staircase and Curve-Like Effect Alleviation
The essential idea of denoising is to obtain the cartoon part of the image  , preserve more details of the edge and texture parts
, preserve more details of the edge and texture parts  , and filter out the noise part
, and filter out the noise part  . In classical TV algorithm and Curvelet threshold algorithm, the staircase effects and curve-like artifacts are often generated in the restored cartoon part
. In classical TV algorithm and Curvelet threshold algorithm, the staircase effects and curve-like artifacts are often generated in the restored cartoon part  , respectively. Our model provides a similar ways to force gradient to be close to an approximation. However, our model provides a better mechanism to alleviate the staircase effects and curve-like artifacts.
, respectively. Our model provides a similar ways to force gradient to be close to an approximation. However, our model provides a better mechanism to alleviate the staircase effects and curve-like artifacts.
Firstly, the "TVGF" model in [7] uses the Gaussian filtering to approximation. However, because Gaussian filter is uniform smoothing in all directions of an image, it will smooth the image too much to preserve edges. Consequently, their gradient fidelity term cannot maintain the variation of intensities well. Differing from the TVGF model, our model takes full advantage of curvelet transform. The curvelets allow an almost optimal sparse representation of object with  -singularities. For a smooth object
-singularities. For a smooth object  with discontinuities along
with discontinuities along  -continuous curves, the best
-continuous curves, the best  -term approximation
-term approximation  by curvelet thresholding obeys
by curvelet thresholding obeys  , while for the wavelets the decay rate is only
, while for the wavelets the decay rate is only  .
.
Secondly, from the regularization theory, the gradient fidelity term  works as Tikhonov regularization in Sobolev functional space
works as Tikhonov regularization in Sobolev functional space  The problem of
The problem of  admits a unique solution characterized by the Euler-Lagrange equation
admits a unique solution characterized by the Euler-Lagrange equation  Moreover, the function
Moreover, the function  is called harmonic (subharmonic, superharmonic)
is called harmonic (subharmonic, superharmonic)  if it satisfies
if it satisfies  . Using the mean value theorems [25], for any ball
. Using the mean value theorems [25], for any ball  , we have
, we have

However, in [7], the gradient fidelity term is chosen as

Comparing the above two results, we can understand the difference between two gradient fidelity term smoothing mechanism. We remark that the gradient fidelity term in [7] will tend to produce more edge blurring effect and remove more texture components with the increasing of the scale parameter  of Gaussian kernel, although it helps to alleviate the staircase effect and produces some smoother results. However, our model tends to produce the curvelet shrinkage image and can remain the curve singularities in images; thus it will obtain good edge preserving performance.
of Gaussian kernel, although it helps to alleviate the staircase effect and produces some smoother results. However, our model tends to produce the curvelet shrinkage image and can remain the curve singularities in images; thus it will obtain good edge preserving performance.
In addition, another rationale behind our proposed model is that the spatially varying fidelity parameters  and
and  are incorporated into our model. In our proposed algorithm, as described in (36), we use the measure
are incorporated into our model. In our proposed algorithm, as described in (36), we use the measure  ; here
; here  is the local power of the residue
is the local power of the residue  . In the flat area where
. In the flat area where  (basic cartoon model without textures or fine-scale details), the local power of the residue is almost constant
(basic cartoon model without textures or fine-scale details), the local power of the residue is almost constant  and hence
and hence  . We get a high-quality denoising process
. We get a high-quality denoising process  so that the noise, the staircase effect, and the curve-like artifacts are smoothed. In the texture area, since the noise is uncorrelated with the signal, thus the total power of the residue can be approximated as
so that the noise, the staircase effect, and the curve-like artifacts are smoothed. In the texture area, since the noise is uncorrelated with the signal, thus the total power of the residue can be approximated as  , the sum of local powers of the noncartoon part and the noise, respectively. Therefore, textured regions are characterized by high local power of the residue. Thus, our algorithm will reduce the level of filtering so that it will preserve the detailed structure of such regions.
, the sum of local powers of the noncartoon part and the noise, respectively. Therefore, textured regions are characterized by high local power of the residue. Thus, our algorithm will reduce the level of filtering so that it will preserve the detailed structure of such regions.
4. Experimental Results and Analysis
In this section, experimental results are presented to demonstrate the capability of our proposed model. The results are compared with those obtained by using the curvelet shrinkage method [26], the "TV" model (2) proposed by Rudin et al. [8], and the "TVGF" model proposed by Zhu and Xia [7].
In the curvelet shrinkage method, denoising is achieved by hard-thresholding of the curvelet coefficients. We select the thresholding at  for all but the finest scale where it is set at
for all but the finest scale where it is set at  ; here
; here  is the noise level of a coefficient at scale
is the noise level of a coefficient at scale  and angle
and angle  . In our experiments, we actually use a robust estimator to estimate noise level using the following formula:
. In our experiments, we actually use a robust estimator to estimate noise level using the following formula:  , here,
, here,  represents the corresponding curvelet coefficients at scale
represents the corresponding curvelet coefficients at scale  and angle
and angle  , and MED
, and MED represents the medium operator to calculate the medium value for a sequence coefficients.
represents the medium operator to calculate the medium value for a sequence coefficients.
The solution of the "TV" model in (2) is obtained by using the following explicit iterative:

Here  and
and  are set to be 0.02 and 0.01, respectively. The regularization parameter
are set to be 0.02 and 0.01, respectively. The regularization parameter  is dynamically updated to satisfy the noise variance constrains according to (4).
is dynamically updated to satisfy the noise variance constrains according to (4).
The solution of the "TVGF" model is obtained by using the following explicit iterative:

Here the size and standard deviation  of Gaussian lowpass filter
of Gaussian lowpass filter  are set to be 7 and 1, respectively. The evolution step length
are set to be 7 and 1, respectively. The evolution step length  is set to be 0.02. The weight
is set to be 0.02. The weight  is set to be 0.5 as suggested in [7], and
is set to be 0.5 as suggested in [7], and  is dynamically updated according to
is dynamically updated according to

where  is set to be 0.01, and
is set to be 0.01, and  is the noise variance.
is the noise variance.
4.1. Image Quality Assessment
For the following experiments, we compute the quality of restored images by the signal-to-noise ratio (SNR) to compare the performance of different algorithms. Because of the limitation of SNR on capturing the subjective appearance of the results, the mean structure similarity (MSSIM) index as defined in [27] is used to measure the performance of the different methods. As shown by theoretical and experimental analysis [27], the MSSIM index intends to measure the perceptual quality of the images.
SNR is defined by

MSSIM is given by

where  and
and  are the original and the restored images, respectively;
are the original and the restored images, respectively;  is the mean of the image
is the mean of the image  ;
;  and
and  are the image contents at the
are the image contents at the  th local window, respectively;
th local window, respectively;  is the number of local windows in the image;
is the number of local windows in the image;

where  is the mean of the image
is the mean of the image  ;
;  is the standard deviation of the image
is the standard deviation of the image  ;
;  is the covariance of the image
is the covariance of the image  and image
and image  ;
;  are the constants.
are the constants.
In order to evaluate the performance of alleviation of staircase effect and curve-like artifacts, the difference image between the restored image and the original clean image is used to visually judge image quality.
The stopping criterion of both the proposed method, "TV" method, and the "TVGF" method is that the MSSIM reached maximum or the total iteration number reached the maximal iteration number 3000.
4.1.1. Qualitative and Quantitative Results
Firstly, we take "Toys" image (see Figure 4(a)) as the test image, and we add Gaussian noise with standard deviation  (the noisy image is shown in Figure 4(b)). The SNR value of noisy Toys image is 3.99 dB while the value of MSSIM is 0.30. The results of the curvelet shrinkage, the TV algorithm, the TVGF algorithm, and our proposed algorithm are displayed in Figures 5(a)–5(d), respectively. All the algorithm can improve the value of SNR and MSSIM greatly, the value of SNR obtained by our algorithm reaches 14.37 dB, while those obtained by the TVGF model, the curvelet algorithm and the TV model is just 13.28 dB, 13.33 dB, and 14.21 dB, respectively. Similarly, the improvement of MSSIM obtained by our algorithm is the largest among all the algorithms. From this kind of cartoon image, our proposed algorithm does a good job at restoring faint geometrical structures of the image. In order to make better judgement on the visual difference of different restored images of different algorithms, we display the subimages which are cropped from Figures 5(a)–5(d). As illustrated in Figures 6(a)–6(f), the restored image by our proposed image (Figure 6(f)) is more nature than any other restored images as shown in Figures 6(c), 6(d), and 6(e). Figure 7 shows the difference image between "Toys" image and restored "Toys" images in Figure 6. From Figure 6, we can see that our algorithm's restored image has less staircase and curve-like distortion comparing with other algorithm's result.
(the noisy image is shown in Figure 4(b)). The SNR value of noisy Toys image is 3.99 dB while the value of MSSIM is 0.30. The results of the curvelet shrinkage, the TV algorithm, the TVGF algorithm, and our proposed algorithm are displayed in Figures 5(a)–5(d), respectively. All the algorithm can improve the value of SNR and MSSIM greatly, the value of SNR obtained by our algorithm reaches 14.37 dB, while those obtained by the TVGF model, the curvelet algorithm and the TV model is just 13.28 dB, 13.33 dB, and 14.21 dB, respectively. Similarly, the improvement of MSSIM obtained by our algorithm is the largest among all the algorithms. From this kind of cartoon image, our proposed algorithm does a good job at restoring faint geometrical structures of the image. In order to make better judgement on the visual difference of different restored images of different algorithms, we display the subimages which are cropped from Figures 5(a)–5(d). As illustrated in Figures 6(a)–6(f), the restored image by our proposed image (Figure 6(f)) is more nature than any other restored images as shown in Figures 6(c), 6(d), and 6(e). Figure 7 shows the difference image between "Toys" image and restored "Toys" images in Figure 6. From Figure 6, we can see that our algorithm's restored image has less staircase and curve-like distortion comparing with other algorithm's result.
The subimages of the original, noisy, and restored "Toys" in Figure 5: (a) the original image; (b) the noisy image; (c) the restored image by the curvelet Shrinkage method; (d) the restored image by using the "TV" model; (e) the restored image by using the "TVGF" model; (f) the restored image by using our proposed model.
The difference images between the original "Toys" image and restored "Toys" images in Figure 6: (a) by the curvelet Shrinkage method; (b) by using the "TV" model; (c) by using the "TVGF" model; (d) by using our proposed model.
In the second experiments, we take "Boat" as the test image. The "Boat" is a kind of image which contains many linear edges and curve singularities. The restored results are depicted in Figure 8, and the difference images are shown in Figure 9. As expected, our hybrid method is less prone to the staircase effect and curve-like artifacts and takes benefits from the curvelet transform for capturing efficiently the geometrical content of image.
The original, noisy, and restored "Boat" images: (a) the original image; (b) the noisy image (SNR = 7. 36, MSSIM = 0.43); (c) the restored image by the curvelet Shrinkage method (SNR = 13.51, MSSIM = 0.76); (d) the restored image by using the "TV" model (SNR = 14.36, MSSIM = 0.78); (e) the restored image by using the "TVGF" model (SNR = 13.25, MSSIM = 0.76); (f) the restored image by using our proposed model (SNR = 14.67, MSSIM = 0.79).
The difference images between the original "Boat" and restored "Boat" images in Figure 8: (a) by the curvelet Shrinkage method; (b) by using the "TV" model; (c) by using the "TVGF" model; (d) by using our proposed model.
In the third experiments, we carry experiments on "Lena" with different noise level and the standard derivation of Gaussian noise is 20, 25, 30, 35, and 40. Figures 10(a)–10(f) display the results for the noisy "Lena" image when the standard deviation of noise is 40. In this case, the value of SNR and MSSIM of the noisy image is 1.54 dB and 0.15, the value of SNR obtained by our algorithm reaches 14.36 dB, while that obtained by the TVGF model, the curvelet algorithm, and the TV model is just 12.01 dB, 13.72 dB and 12.94 dB, respectively. As we know, the "Lena" image is an international standard test image which not only contains the strong vertical and curve edge but also have hair texture. From the result of curvelet shrinkage (Figure 10(c)), the hair texture and the strong vertical and curve edge are restored very good; however some annoying curve-like artifacts are generated. The TV algorithm can preserve the edge, but it lose the hair texture; moreover, the staircase effect is very obvious (Figure 10(d)). The TVGF algorithm can reduce the staircase effect; however, the edges and textures in "Lena" image look a bit blurred. Compared with the other algorithms, our hybrid algorithm obtains a sharper image with better hair detail, and the restored image is almost free of artifacts. The values of MSSIM of four algorithms also show that our algorithm has the best image perceptual quality. From Table 1, we can find that our algorithm can obtain the largest value of MSSIM. We just display two group results (Figures 10 and 11) for the face part of "Lena" image of various algorithms in the cases of Gaussian noise with standard deviation  , respectively.
, respectively.
The subimages of the original, noisy, and restored "Lena": (a) the original image; (b) the noisy image (SNR = 1. 54, MSSIM = 0.15); (c) the restored image by the curvelet shrinkage method (SNR = 13.72, MSSIM = 0.79); (d) the restored image by using the "TV" model (SNR = 12.94, MSSIM = 0.71); (e) the restored image by using the "TVGF" model (SNR = 12.01, MSSIM = 0.61); (f) the restored image by using the proposed model (SNR = 14.36, MSSIM = 0.82).
The difference images between the original "Lena" and restored "Lena" images in Figure 10: (a) by the curvelet Shrinkage method; (b) by using the "TV" model; (c) by using the "TVGF" model; (d) by using our proposed model.
In the fourth experiments, we take "Barbara" as the test image. The "Barbara" is a kind of image which contains many texture details. The distinguished characteristic of the Barbara image is that it has abundant textures. We display two group results (Figures 12, 13, 14, and 15) for the face part of "Barbara" image of various algorithms in the cases of Gaussian noise with standard deviation  and
and  , respectively. From these experiments, the visual quality of restored image of our algorithm is better than any other algorithms. Of course, our hybrid algorithm can only restore the regular texture partially, some tiny textures cannot be restored, but the whole image looks more nature and more harmonious.
, respectively. From these experiments, the visual quality of restored image of our algorithm is better than any other algorithms. Of course, our hybrid algorithm can only restore the regular texture partially, some tiny textures cannot be restored, but the whole image looks more nature and more harmonious.
The detail of the original, noisy, and restored "Barbara" images: (a) the original image; (b) the noisy image (SNR = 8. 73, MSSIM = 0.48); (c) the restored image by the curvelet shrinkage method (SNR = 12.05, MSSIM = 0.77); (d) the restored image by using the "TV" model (SNR = 12.74, MSSIM = 0.77); (e) the restored image by using the "TVGF" model (SNR = 11.39, MSSIM = 0.72); (f) the restored image by using our proposed model (SNR = 13.15, MSSIM = 0.81).
The difference images between the original "Barbara" and restored "Barbara" images in Figure 12: (a) by the curvelet Shrinkage method; (b) by using the "TV" model; (c) by using the "TVGF" model; (d) by using our proposed model.
The subimages of the original, noisy, and restored "Barbara" images: (a) the original image; (b) the noisy image (SNR = 2. 71, MSSIM = 0.26); (c) the restored image by Curvelet Shrinkage method (SNR = 10.45, MSSIM = 0.68); (d) the restored image by using the "TV" model (SNR = 10.12, MSSIM = 0.61); (e) the restored image by using the "TVGF" model (SNR = 9.93, MSSIM = 0.56); (f) the restored image by using our proposed model (SNR = 10.81, MSSIM = 0.70).
The difference images between the original "Barbara" and restored "Barbara" images in Figure 14: (a) by the curvelet Shrinkage method; (b) by using the "TV" model; (c) by using the "TVGF" model; (d) by using our proposed model.
In addition, we use the SNR and MSSIM index to evaluate the quality of restored images of various algorithms under different noise level. For fair comparison, all the results are the images whose values of MSSIM reach maximum in their iterative process, respectively. In order to systematically evaluate the performance of the various algorithms from different noise levels, the denoising performance results are tabulated in Tables 1 and 2 for the "Lena" image and the "Barbara" image, respectively. By inspection of these tables, both the SNR improvement and the MSSIM improvement by our model are larger than the other three models. It is interesting to point out that the performance of the TVGF algorithm is not good compared with three other algorithms. This phenomenon has been discussed and analyzed by the research of literature [28] and the reason is the blurring caused by Gaussian kernel convolution. Of course, the TVGF algorithm actually reduces the staircase effect to some extent. Differing with Gaussian kernel convolution, our proposed algorithm takes advantage of the anisotropic of the curvelets; therefore there is no any edge blurring. The MSSIM improvement shows that our algorithm has better "subjective" or perceptual quality. Especially, the important improvement becomes more salient as noise level increase. Also we can see, both the SNR improvement and the MSSIM improvement obtained by our algorithm become more salient than those obtained by other algorithms for more complex images with more textures, for instance, the Barbara image. Figures 16, 17, 18, and 19 show the amplitude of the MSSIM improvement during the iterative process of the TV model, the TVGF model, and our proposed model. Tables 1 and 2 also list the total iteration number of each algorithm. For example, in Table 1, when the noise standard deviation is 40, the "TV" model needs 3000 iteration steps to reach the maximum MSSIM (0.71), the "TVGF" model needs 1151 iteration steps to reach the maximum MSSIM (0.61), the "TVGF" model needs 1151 iteration steps to reach the maximum MSSIM (0.61), while our model can obtain the good quality restored image with the value of MSSIM being 0.82 using 1033 iteration steps. These experiments show that our algorithm can more quickly reach the best restored image with maximum MSSIM, and our algorithm obtains the best performance comparing with the other algorithms.
5. Conclusion
In this paper, a curvelet shrinkage fidelity-based total variation regularization is proposed for discontinuity-preserving denoising. We propose a new gradient fidelity term, which is designed to force the gradients of desired image to be close to the curvelet approximation gradients. To improve the ability of preserving the details of edges and texture, the spatial-varying parameters are adaptively estimated in the iterative process of the gradient descent flow algorithm. We carry out many numerical experiments to compare the performance of various algorithms. The SNR and MSSIM improvements demonstrate that our proposed method has the best performance than the TV algorithm, the curvelet shrinkage, and the TVGF algorithm. Our future work will extend this new gradient fidelity term to other PDE-based methods.
References
Buades A, Coll B, Morel JM: A review of image denoising algorithms, with a new one. Multiscale Modeling and Simulation 2005, 4(2):490-530. 10.1137/040616024
Do MN, Vetterli M: The contourlet transform: an efficient directional multiresolution image representation. IEEE Transactions on Image Processing 2005, 14(12):2091-2106.
Candès E, Donoho D: Curvelets-a surprisingly effective nonadaptive representation for objects with edges. In Curves and Surface Fitting: Saint-Malo 1999. Edited by: Cohen A, Rabut C, Schumaker L. Vanderbilt University Press, Nashville, Tenn, USA; 2000:105-120.
Candès EJ, Donoho DL:New tight frames of curvelets and optimal representations of objects with piecewise
 singularities. Communications on Pure and Applied Mathematics 2004, 57(2):219-266. 10.1002/cpa.10116
singularities. Communications on Pure and Applied Mathematics 2004, 57(2):219-266. 10.1002/cpa.10116Candès E, Demanet L, Donoho D, Ying L: Fast discrete curvelet transforms. Multiscale Modeling and Simulation 2006, 5(3):861-899. 10.1137/05064182X
Ma J, Plonka G: Combined curvelet shrinkage and nonlinear anisotropic diffusion. IEEE Transactions on Image Processing 2007, 16(9):2198-2206.
Zhu L, Xia D: Staircase effect alleviation by coupling gradient fidelity term. Image and Vision Computing 2008, 26(8):1163-1170. 10.1016/j.imavis.2008.01.008
Rudin LI, Osher S, Fatemi E: Nonlinear total variation based noise removal algorithms. Physica D 1992, 60(1–4):259-268.
Perona P, Malik J: Scale-space and edge detection using anisotropic diffusion. IEEE Transactions on Pattern Analysis and Machine Intelligence 1990, 12(7):629-639. 10.1109/34.56205
Alvarez L, Lions P, Morel J: Image selective smoothing and edge detection by nonlinear diffusion. II. SIAM Journal on Numerical Analysis 1992, 29(3):845-866. 10.1137/0729052
Chan T, Esedoglu S, Park F, Yip A: Recent developments in total variation image restoration. In Handbook of Mathematical Models in Computer Vision. Edited by: Paragios N, Chen Y, Faugeras O. Springer, Berlin, Germany; 2004.
Lysaker M, Tai X-C: Iterative image restoration combining total variation minimization and a second-order functional. International Journal of Computer Vision 2006, 66(1):5-18. 10.1007/s11263-005-3219-7
Li F, Shen C, Fan J, Shen C: Image restoration combining a total variational filter and a fourth-order filter. Journal of Visual Communication and Image Representation 2007, 18(4):322-330. 10.1016/j.jvcir.2007.04.005
Gilboa G, Zeevi YY, Sochen N: Texture preserving variational denoising usingan adaptive fidelity term. Proceedings of the 2nd IEEE Workshop on Variational, Geometric and Level Set Methods in Computer Vision (VLSM '03), 2003, Nice, France 137-144.
Ma J, Fenn M: Combined complex ridgelet shrinkage and total variation minimization. SIAM Journal of Scientific Computing 2006, 28(3):984-1000. 10.1137/05062737X
Plonka G, Steidl G: A multiscale wavelet-inspired scheme for nonlinear diffusion. International Journal of Wavelets, Multiresolution and Information Processing 2006, 4(1):1-21. 10.1142/S0219691306001063
Ma J, Fenn M: Combined complex ridgelet shrinkage and total variation minimization. SIAM Journal of Scientific Computing 2006, 28(3):984-1000. 10.1137/05062737X
Ying L, Demanet L, Candès E: 3D discrete curvelet transform. Wavelets XI, August 2005, San Diego, Calif, USA, Proceedings of SPIE 1-11.
Demanet L, Ying L: Curvelets and wave atoms for mirror-extended images. Wavelets XII, August 2007, San Diego, Calif, USA, Proceedings of SPIE
Achim A, Tsakalides P, Bezerianos A: SAR image denoising via Bayesian wavelet shrinkage based on heavy-tailed modeling. IEEE Transactions on Geoscience and Remote Sensing 2003, 41(8):1773-1784. 10.1109/TGRS.2003.813488
Durand S, Nikolova M:Denoising of frame coefficients using
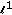 data-fidelity term and edge-preserving regularization. Multiscale Modeling & Simulation 2007, 6(2):547-576. 10.1137/06065828X
data-fidelity term and edge-preserving regularization. Multiscale Modeling & Simulation 2007, 6(2):547-576. 10.1137/06065828XDonoho DL, Johnstone IM: Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81(3):425-455. 10.1093/biomet/81.3.425
Kornprobst P, Deriche R, Aubert G: Image sequence analysis via partial differential equations. Journal of Mathematical Imaging and Vision 1999, 11(1):5-26. 10.1023/A:1008318126505
Xiao L, Huang L-L, Wei Z-H: A weberized total variation regularization-based image multiplicative noise removal algorithm. EURASIP Journal on Advances in Signal Processing 2010, 2010:-15.
Gilbarg D, Trudinger NS: Elliptic Partial Differential Equation of Second Order. Springer, Berlin, Germany; 2003.
Starck J-L, Candès EJ, Donoho DL: The curvelet transform for image denoising. IEEE Transactions on Image Processing 2002, 11(6):670-684. 10.1109/TIP.2002.1014998
Wang Z, Bovik AC, Sheikh HR, Simoncelli EP: Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing 2004, 13(4):600-612. 10.1109/TIP.2003.819861
Dong FF, Liu Z: A new gradient fidelity for avoiding staircasing effect. Journal of Computer Science and Technology 2009, 24(6):1162-1170. 10.1007/s11390-009-9289-1
Acknowledgments
The authors would like to express their gratitude to the anonymous referees for making helpful and constructive suggestions. The authors also thank financial support from the National Natural Science Foundation of China (60802039) and the National 863 High Technology Development Project (2007AA12Z142), Specialized Research Fund for the Doctoral Program of Higher Education (20070288050), and NUST Research Funding under Grant no. 2010ZDJH07.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Xiao, L., Huang, LL. & Roysam, B. Image Variational Denoising Using Gradient Fidelity on Curvelet Shrinkage. EURASIP J. Adv. Signal Process. 2010, 398410 (2010). https://doi.org/10.1155/2010/398410
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/398410




 . (c)–(f) Denoising of "Toys" image shown in (b) where the curvelet transform is hard-thresholding according to (17) for different choices of
. (c)–(f) Denoising of "Toys" image shown in (b) where the curvelet transform is hard-thresholding according to (17) for different choices of  .Toys imageNoisy for
.Toys imageNoisy for 




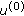 and obtain the discrete coefficients
and obtain the discrete coefficients 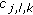 .
. , and then use the shrinkage operator in (33) to obtain the estimated coefficients
, and then use the shrinkage operator in (33) to obtain the estimated coefficients 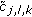 .
. .
.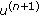 according to (40).
according to (40).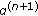 according to (36).
according to (36). according to (38).
according to (38).














 singularities. Communications on Pure and Applied Mathematics 2004, 57(2):219-266. 10.1002/cpa.10116
singularities. Communications on Pure and Applied Mathematics 2004, 57(2):219-266. 10.1002/cpa.10116 data-fidelity term and edge-preserving regularization. Multiscale Modeling & Simulation 2007, 6(2):547-576. 10.1137/06065828X
data-fidelity term and edge-preserving regularization. Multiscale Modeling & Simulation 2007, 6(2):547-576. 10.1137/06065828X