- Research Article
- Open access
- Published:
A Content-Motion-Aware Motion Estimation for Quality-Stationary Video Coding
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 403634 (2010)
Abstract
The block-matching motion estimation has been aggressively developed for years. Many papers have presented fast block-matching algorithms (FBMAs) for the reduction of computation complexity. Nevertheless, their results, in terms of video quality and bitrate, are rather content-varying. Very few FBMAs can result in stationary or quasistationary video quality for different motion types of video content. Instead of using multiple search algorithms, this paper proposes a quality-stationary motion estimation with a unified search mechanism. This paper presents a content-motion-aware motion estimation for quality-stationary video coding. Under the rate control mechanism, the proposed motion estimation, based on subsample approach, adaptively adjusts the subsample ratio with the motion-level of video sequence to keep the degradation of video quality low. The proposed approach is a companion for all kinds of FBMAs in H.264/AVC. As shown in experimental results, the proposed approach can produce stationary quality. Comparing with the full-search block-matching algorithm, the quality degradation is less than 0.36 dB while the average saving of power consumption is 69.6%. When applying the proposed approach for the fast motion estimation (FME) algorithm in H.264/AVC JM reference software, the proposed approach can save 62.2% of the power consumption while the quality degradation is less than 0.27 dB.
1. Introduction
Motion Estimation (ME) has been proven to be effective to exploit the temporal redundancy of video sequences and, therefore, becomes a key component of multimedia standards, such as MPEG standards and H.26X [1–7]. The most popular algorithm for the VLSI implementation of motion estimation is the block-based full search algorithm [8–11]. The block-based full search algorithm has high degree of modularity and requires low control overhead. However, the full search algorithm notoriously needs high computation load and large memory size [12–14]. The highly computational cost has become a major problem on the implementation of motion estimation.
To reduce the computational complexity of the full-search block-matching (FSBM) algorithm, researchers have proposed various fast algorithms. They either reduce search steps [12, 15–22] or simplify calculations of error criterion [8, 23–25]. Some researchers combined both step-reduction and criterion-simplifying to significantly reduce computational load with little degradation. By combining step-reduction and criterion-simplifying, some researchers proposed two-phase algorithms to balance the performance between complexity and quality [26–28]. These fast algorithms have been shown that they can significantly reduce the computational load while the average quality degradation is little. However, a real video sequence may have different types of content, such as slow-motion, moderate-motion, and fast-motion, and little quality degradation in average does not imply the quality is acceptable all the time. The fast block-matching algorithms (FBMAs) mentioned above are all independent of the motion type of video content, and their quality degradation may considerably vary within a real video sequence.
Few papers present quality-stationary motion estimation algorithms for video sequences with mixed fast-motion, moderate-motion, and slow-motion content. Huang et al. [29] propose an adaptive, multiple-search-pattern FBMA, called the A-TDB algorithm, to solve the content-dependent problem. Motivated by the characteristics of three-step search (TSS), diamond search (DS), and block-based gradient descent search (BBGDS), the A-TDB algorithm dynamically switches search patterns according to the motion type of video content. Ng et al. [30] propose an adaptive search patterns switching (SPS) algorithm by using an efficient motion content classifier based on error descent rate (EDR) to reduce the complexity of the classification process of the A-TDB algorithm. Other multiple search algorithms have been proposed [31, 32]. They showed that using multiple search patterns in ME can outperform stand-alone ME techniques.
Instead of using multiple search algorithms, this paper intends to propose a quality-stationary motion estimation with a unified search mechanism. The quality-stationary motion estimation can appropriately adjust the computational load to deliver stationary video quality for a given bitrate. Herein, we used the subsample or pixel-decimation approach for the motion-vector (MV) search. The use of subsample approach is two-folded. First, the subsample approach can be applied for all kinds of FBMAs and provide high degree of flexibility for adaptively adjusting the computational load. Secondly, the subsample approach is feasible and scalable for either hardware or software implementation. The proposed approach is not limited for FSBM, but valid for all kinds of FBMAs. The proposed approach is a companion for all kinds of FBMAs in H.264/AVC.
Articles in [33–38] present the subsample approaches for motion estimation. The subsample approaches are used to reduce the computational cost of the block-matching criterion evaluation. Because the subsample approaches always desolate some pixels, the accuracy of the estimated MVs becomes the key issue to be solved. As per the fundamental of sampling, downsampling a signal may result in aliasing problem. The narrower the bandwidth of the signal, the lower the sampling frequency without aliasing problem will be. The published papers [33–38] mainly focus on the subsample pattern based on the intraframe high-frequency pixels (i.e., edges). Instead of considering spatial frequency bandwidth, to be aware of the content motion, we determine the subsample ratio by temporal bandwidth. Applying high subsample ratio for slow motion blocks would not reduce the accuracy for slow motion or result in large amount of prediction residual. Note that the amount of prediction residual is a good measure of the compressibility. Under a fixed bit-rate constraint, the compressibility affects the compression quality. Our algorithm can adaptively adjust the subsample ratio with the motion-level of video sequence. When the interframe variation becomes high, we consider the motion-level of interframe as the fast-motion and apply low subsample ratio for motion estimation. When the interframe variation becomes low, we apply high subsample ratio for motion estimation.
Given the acceptable quality in terms of PSNR and bitrate, we successfully develop an adaptive motion estimation algorithm with variable subsample ratios. The proposed algorithm is awared of the motion-level of content and adaptively select the subsample ratio for each group of picture (GOP). Figure 1 shows the application of proposed algorithm. The scalable fast ME is an adjustable motion estimation whose subsampling ratio can be tuned by the motion-level detection. The dash-lined region is the proposed motion estimation algorithm and the proposed algorithm switches the subsample ratios according to the zero motion vector count (ZMVC). The higher the ZMVC, the higher the subsample ratio. As the result of applying the algorithm for H.264/AVC applications, the proposed algorithm can produce stationary quality at the PSNR of 0.36 dB for a given bitrate while saving about 69.6% power consumption for FSBM, and the PSNR of 0.27 dB and 62.2% power-saving for FBMA. The rest of the paper is organized as follows. In Section 2, we introduce the generic subsample algorithm in detail. Section 3 describes the high-frequency aliasing problem in the subsample algorithm. Section 4 describes the proposed algorithm. Section 5 shows the experimental performance of the proposed algorithm in H.264 software model. Finally, Section 6 concludes our contribution and merits of this work.
2. Generic Subsample Algorithm
Among many efficient motion estimation algorithms, the FSBM algorithm with sum of absolute difference (SAD) is the most popular approach for motion estimation because of its considerably good quality. It is particularly attractive to ones who require extremely high quality, however, it requires a huge number of arithmetic operations and results in highly computational load and power dissipation. To efficiently reduce the computational complexity of FSBM, lots of published papers have efficiently presented fast algorithms for motion estimation. For these fast algorithms, much research addresses subsample technologies to reduce the computational load of FSBM [33–37, 39, 40]. Liu and Zaccarin [33], as pioneers of subsample algorithm, applied subsampling technology to FSBM and significantly reduced the computation load. Cheung and Po [34] well proposed a subsample algorithm combined with hierarchical-search method. Here, we present a generic subsample algorithm in which the subsample ratio ranges from  -to-
-to- to
to  -to-
-to- . The basic operation of the generic subsample algorithm is to find the best motion estimation with less SAD computation. The generic subsample algorithm uses (1) as a matching criterion, called the subsample sum of absolute difference (SSAD), where the macroblock size is N-by-N, R(i,j) is the luminance value at
. The basic operation of the generic subsample algorithm is to find the best motion estimation with less SAD computation. The generic subsample algorithm uses (1) as a matching criterion, called the subsample sum of absolute difference (SSAD), where the macroblock size is N-by-N, R(i,j) is the luminance value at  of the current macroblock (CMB). The
of the current macroblock (CMB). The  is the luminance value at
is the luminance value at  of the reference macroblock (RMB) which offsets
of the reference macroblock (RMB) which offsets  from the CMB in the searching area
from the CMB in the searching area  -by-
-by- .
.  is the subsample mask for the subsample ratio
is the subsample mask for the subsample ratio  -to-
-to- as shown in (2) and the subsample mask
as shown in (2) and the subsample mask  is generated from basic mask (BM) as shown in (3), When the subsample ratios are fixed at powers of two because of regularly spatial distribution, these ratios are 16 : 16, 16 : 8, 16 : 4, and 16 : 2, respectively. These subsample masks can be generated in a 16-by-16 macroblock by using (3) and are shown in Figure 2. From (3), given a subsample mask generated, the computational cost of SSAD can be lower than that of SAD calculation, hence, the generic subsample algorithm can achieve the goal of power-saving with flexibly changing subsample ratio. However, the generic subsample algorithm suffers aliasing problem for high-frequency band. The aliasing problem will degrade the validity of motion vector (MV) and obviously result in a visual quality degradation for some video sequences. The next section will describe how the high-frequency aliasing problem occurs for subsample algorithm in detail,
is generated from basic mask (BM) as shown in (3), When the subsample ratios are fixed at powers of two because of regularly spatial distribution, these ratios are 16 : 16, 16 : 8, 16 : 4, and 16 : 2, respectively. These subsample masks can be generated in a 16-by-16 macroblock by using (3) and are shown in Figure 2. From (3), given a subsample mask generated, the computational cost of SSAD can be lower than that of SAD calculation, hence, the generic subsample algorithm can achieve the goal of power-saving with flexibly changing subsample ratio. However, the generic subsample algorithm suffers aliasing problem for high-frequency band. The aliasing problem will degrade the validity of motion vector (MV) and obviously result in a visual quality degradation for some video sequences. The next section will describe how the high-frequency aliasing problem occurs for subsample algorithm in detail,



where u(n) is a step function; that is,

3. High-Frequency Aliasing Problem
According to sampling theory [41], the decrease of sampling frequency will result in aliasing problem for high-frequency band. On the other hand, when the bandwidth of signal is narrow, higher downsample ratio or lower sampling frequency is allowed without aliasing problem. When applying the generic subsample algorithm for video compression, for high-variation sequences, the aliasing problem occurs and leads to considerable quality degradation because the high-frequency band is messed up. Papers [42, 43] hence propose adaptive subsample algorithms to solve the problem. They employed the variable subsample pattern for spatial high-frequency band, that is, edge pixels. However, the motion estimation is used for interframe prediction and temporal high-frequency band should be mainly treated carefully. Therefore, we determine the subsample ratio by the interframe variation. The interframe variation can be characterized by the motion-level of content. The ZMVC is a good sign for the motion-level detection because it is feasible for measurement and requires low computation load. The high ZMVC means that the interframe variation is low and vice versa. Hence, we can set high subsample ratio for high ZMVCs and low subsample ratio for low ZMVCs. Doing so, the aliasing problem can be alleviated and the quality can be frozen within an acceptable range.
To start with, we first analyze the results of visual quality degradation with different subsample ratios. We simulated the moderate motion video sequence "table" in H.264 JM10.2 software, where the length of GOP is fifteen frames, the frame rate is 30 frames/s, the bit rate is 450 k bits/s, and initial  is 34. After applying three subsample ratios of 16 : 8, 16 : 4, and 16 : 2, Figure 3 shows quality degradation results versus subsample ratios. The average quality degradation of the i th GOP (
is 34. After applying three subsample ratios of 16 : 8, 16 : 4, and 16 : 2, Figure 3 shows quality degradation results versus subsample ratios. The average quality degradation of the i th GOP ( ) is defined as (5), where
) is defined as (5), where  is the average PSNRY of i th GOP using the full-search block-matching (FSBM) and
is the average PSNRY of i th GOP using the full-search block-matching (FSBM) and  is the average PSNRY of i th GOP with specific subsample ratio (SSR). From Figure 3, although the video sequence "table" is, in the literature, regarded as a moderate motion, there exists the high interframe variation between the third GOP and the seventh GOP. Obviously, applying the higher subsample ratios may result in serious aliasing problem and higher degree of quality degradation. In contrast, between the eleventh GOP and the twentieth GOP, the quality degradation is low for lower subsample ratios. Therefore, we can vary the subsample ratio with the motion-level of content to produce quality-stationary video while saving the power consumption when necessary. Accordingly, we developed a content-motion-aware motion estimation based on the motion-level detection. The proposed motion estimation is not limited for FSBM, but valid for all kinds of FBMAs,
is the average PSNRY of i th GOP with specific subsample ratio (SSR). From Figure 3, although the video sequence "table" is, in the literature, regarded as a moderate motion, there exists the high interframe variation between the third GOP and the seventh GOP. Obviously, applying the higher subsample ratios may result in serious aliasing problem and higher degree of quality degradation. In contrast, between the eleventh GOP and the twentieth GOP, the quality degradation is low for lower subsample ratios. Therefore, we can vary the subsample ratio with the motion-level of content to produce quality-stationary video while saving the power consumption when necessary. Accordingly, we developed a content-motion-aware motion estimation based on the motion-level detection. The proposed motion estimation is not limited for FSBM, but valid for all kinds of FBMAs,

4. Adaptive Motion Estimation with Variable Subsample Ratios
To efficiently alleviate the high-frequency aliasing problem and maintain the visual quality for video sequences with variable motion levels, we propose an adaptive motion estimation algorithm with variable subsample ratios, called the Variable Subsampling Motion Estimation (VSME). The proposed algorithm determines the suitable subsample ratio for each GOP based on the ZMVC. The algorithm can be applied for FSBM algorithm and all other FBMAs. The ZMVC is a feasible measurement for indicating the motion-level of video. The higher the ZMVC, the lower the motion-level. Figure 4 shows the ZMVC of first P-frame in each GOP for table sequence. From Figures 3 and 4, we can see that when the ZMVC is high the  for the subsample ratio of 16 : 2 is little. Since the tenth GOP is the scene-changing segment, all subsampling algorithms will fail to maintain the quality. Between the third and seventh GOPs,
for the subsample ratio of 16 : 2 is little. Since the tenth GOP is the scene-changing segment, all subsampling algorithms will fail to maintain the quality. Between the third and seventh GOPs,  becomes high and the ZMVC is relatively low. Thus, this paper uses the ZMVC as a reference to determine the suitable subsample ratio.
becomes high and the ZMVC is relatively low. Thus, this paper uses the ZMVC as a reference to determine the suitable subsample ratio.
In the proposed algorithm, we determine the subsample ratio at the beginning of each GOP because the ZMVC of the first interframe prediction is the most accurate. The reference frame in the first interframe prediction is a reconstructed I-frame but others are not for each GOP. Only the reconstructed I-frame does not incur the influence resulted from the quality degradation of the inaccurate interframe prediction. That is, we only calculate the ZMVC of the first P-frame for the subsample ratio selection to efficiently save the computational load of ZMVC. Note that the ZMVC of the first P-frame is calculated by using 16 : 16 subsample ratio. Given the ZMVC of the first P-frame, the motion-level is determined by comparing the ZMVC with preestimated threshold values. The threshold values is decided statistically using popular video clips.
To set the threshold values for motion-level detection, we first built up the statistical distribution of  versus ZMVC for video sequences with subsample ratios of 16 : 2, 16 : 4, 16 : 8, and 16 : 16. Figure 5 illustrates the distribution. Then, we calculated the coverage of given PSNR degradation
versus ZMVC for video sequences with subsample ratios of 16 : 2, 16 : 4, 16 : 8, and 16 : 16. Figure 5 illustrates the distribution. Then, we calculated the coverage of given PSNR degradation  . In the video coding community, 0.5 dB is empirically considered a threshold below which the perceptual quality difference cannot be perceived by subjects. The quality degradation of greater than 0.5 dB is sensible for human perception [44]. To keep the degradation of video quality low for the quality-stationary video coding, a strict threshold of smaller than 0.5 dB is assigned to be a aimed
. In the video coding community, 0.5 dB is empirically considered a threshold below which the perceptual quality difference cannot be perceived by subjects. The quality degradation of greater than 0.5 dB is sensible for human perception [44]. To keep the degradation of video quality low for the quality-stationary video coding, a strict threshold of smaller than 0.5 dB is assigned to be a aimed  without the sensible quality degradation. Therefore, in this paper, the aimed
without the sensible quality degradation. Therefore, in this paper, the aimed  is 0.3 dB. We use the coverage range
is 0.3 dB. We use the coverage range  to set the threshold values for motion-level detection. The motion-level detection will further determine the subsample ratio. The range
to set the threshold values for motion-level detection. The motion-level detection will further determine the subsample ratio. The range  indicates the covered range of ZMVC, where
indicates the covered range of ZMVC, where  is the percentage of GOPs whose
is the percentage of GOPs whose  is less than 0.3 dB for subsample ratio of
is less than 0.3 dB for subsample ratio of  . Given the parameters
. Given the parameters  and
and  , we can set threshold values as shown in Table 1.
, we can set threshold values as shown in Table 1.
 of visual quality degradation.
of visual quality degradation.5. Selection of ZMVC Threshold and Simulation Results
The proposed algorithm is simulated for H.264 video coding standard by using software model JM10.2 [45]. Here, we use twelve famous video sequences [46] to simulate in JM10.2, and they are shown in Figure 6 and Table 2. From Table 2, the file format of these video sequences is CIF (352 288 pixels) and the search range is
288 pixels) and the search range is  16 in both horizontal and vertical directions for a 16-16 macroblock. The bit-rate control fixes the bit rate of 450 k under displaying 30 frames/s. The selection of threshold values is based on two factors: average quality degradation (
16 in both horizontal and vertical directions for a 16-16 macroblock. The bit-rate control fixes the bit rate of 450 k under displaying 30 frames/s. The selection of threshold values is based on two factors: average quality degradation ( PSNRY) and average subsample ratio. The PSNRY is defined as
PSNRY) and average subsample ratio. The PSNRY is defined as

where the frame size is  , and
, and  and
and  denote the Y components of original frame and reconstructed frame at
denote the Y components of original frame and reconstructed frame at  . The quality degradation
. The quality degradation  PSNRY is the PSNRY difference between the proposed algorithm and FSBM algorithm with 16-to-16 subsample ratio.
PSNRY is the PSNRY difference between the proposed algorithm and FSBM algorithm with 16-to-16 subsample ratio.
The average subsample ratio is another index for subsample ratio selection, as defined in (7) where  are the P-frames subsampled by
are the P-frames subsampled by  . Later, we will use it to estimate the average power consumption of the proposed algorithm,
. Later, we will use it to estimate the average power consumption of the proposed algorithm,

Table 3 shows the simulation results of  PSNRY for these tested video sequences with different set of threshold values. From Table 3, the set of threshold values with
PSNRY for these tested video sequences with different set of threshold values. From Table 3, the set of threshold values with  can satisfy all tested video sequences under the average quality degradation of 0.3 dB; however, the overall average subsample ratios shown in Table 4 are lower than the others. The lower the subsample ratio, the higher the computational power will be. The uses of the set of threshold values of
can satisfy all tested video sequences under the average quality degradation of 0.3 dB; however, the overall average subsample ratios shown in Table 4 are lower than the others. The lower the subsample ratio, the higher the computational power will be. The uses of the set of threshold values of  and
and  also result in the quality degradations less than 0.36 dB which is close to the 0.3 dB goal. To achieve the goal of the quality degradation under the low computational power, the set of threshold values with
also result in the quality degradations less than 0.36 dB which is close to the 0.3 dB goal. To achieve the goal of the quality degradation under the low computational power, the set of threshold values with  is favored in this paper. As shown in Table 4, the use of the set of threshold values of
is favored in this paper. As shown in Table 4, the use of the set of threshold values of  results in the quality degradations less than 0.36 dB which is close to the 0.3 dB goal while the power consumption reduction is 69.6% comparing with FSBM without downsampling.
results in the quality degradations less than 0.36 dB which is close to the 0.3 dB goal while the power consumption reduction is 69.6% comparing with FSBM without downsampling.
After choosing the set of threshold values between 16 : 16, 16 : 8, 16 : 4, and 16 : 2, we compare the proposed algorithm with generic subsample rate algorithms. Table 5 illustrates the simulation results. Figure 7 illustrates the distribution diagram of  PSNRY versus subsample ratio based on Table 5. From Figure 7, to maintain
PSNRY versus subsample ratio based on Table 5. From Figure 7, to maintain  PSNRY around 0.3 dB, the generic algorithm must at least use the fixed 16 : 12 subsample ratio to meet the target, but the proposed algorithm can adaptively use lower subsample ratio to save power dissipation while the degradation goal is met. To demonstrate that the proposed algorithm can adaptively select the suitable subsample ratios for each GOP of a tested video sequence, we analyze the average quality degradation of each GOP by using (5) for "table" sequence and the result is shown as in Figure 8. From Figure 8, the first, second, eighth to twentieth GOPs have the lowest degree of high-frequency characteristic and their ZMVCs also show that they belong to low motion degree, hence these GOPs are allotted 16 : 2 subsample ratio. Moreover, the third GOP has the highest degree of high-frequency characteristic and this GOP is allotted 16 : 16 subsample ratio. The fourth to seventh GOPs also are allotted the suitable subsample ration according to their ZMVCs. Since the tenth GOP is the scene-changing segment, all subsampling algorithms will fail to maintain the quality. Per our simulation with other scene-changing clips, the proposed algorithm does not always miss the optimal ratio. However, in average, the proposed can perform better quality results than the others. Figure 9 shows comparison the PSNRY of each frame using proposed algorithm with the PSNRY of each frame using fixed 16 : 16, 16 : 6, and 16 : 4 subsample ratios. From the analysis result of Figure 9, the PSNRY results of the proposed algorithm is very close to the PSNRY results of fixed 16 : 16 and the proposed algorithm can efficiently save power consumption without affecting visual quality. Finally, to demonstrate the power-saving ability of proposed algorithm, we use (8) to calculate the speedup ratio and the results are shown in Table 6. From Table 6, the speedup ratio can achieve between 1.36 and 5.33. The average speedup ratio is 3.28,
PSNRY around 0.3 dB, the generic algorithm must at least use the fixed 16 : 12 subsample ratio to meet the target, but the proposed algorithm can adaptively use lower subsample ratio to save power dissipation while the degradation goal is met. To demonstrate that the proposed algorithm can adaptively select the suitable subsample ratios for each GOP of a tested video sequence, we analyze the average quality degradation of each GOP by using (5) for "table" sequence and the result is shown as in Figure 8. From Figure 8, the first, second, eighth to twentieth GOPs have the lowest degree of high-frequency characteristic and their ZMVCs also show that they belong to low motion degree, hence these GOPs are allotted 16 : 2 subsample ratio. Moreover, the third GOP has the highest degree of high-frequency characteristic and this GOP is allotted 16 : 16 subsample ratio. The fourth to seventh GOPs also are allotted the suitable subsample ration according to their ZMVCs. Since the tenth GOP is the scene-changing segment, all subsampling algorithms will fail to maintain the quality. Per our simulation with other scene-changing clips, the proposed algorithm does not always miss the optimal ratio. However, in average, the proposed can perform better quality results than the others. Figure 9 shows comparison the PSNRY of each frame using proposed algorithm with the PSNRY of each frame using fixed 16 : 16, 16 : 6, and 16 : 4 subsample ratios. From the analysis result of Figure 9, the PSNRY results of the proposed algorithm is very close to the PSNRY results of fixed 16 : 16 and the proposed algorithm can efficiently save power consumption without affecting visual quality. Finally, to demonstrate the power-saving ability of proposed algorithm, we use (8) to calculate the speedup ratio and the results are shown in Table 6. From Table 6, the speedup ratio can achieve between 1.36 and 5.33. The average speedup ratio is 3.28,

The foregoing simulations are implemented using FSBM algorithm in JM10.2 software. Next, the fast motion estimation (FME) algorithm in JM10.2 software is chosen to combine with the proposed algorithm and implement simulations mentioned above again. Table 7 shows results of  PSNRY between the proposed algorithm and generic algorithm. Figure 10 shows the distribution diagram of
PSNRY between the proposed algorithm and generic algorithm. Figure 10 shows the distribution diagram of  PSNRY versus subsample ratio based on Table 7 and shows that all tested sequences can satisfy to maintain the visual quality degradation under constraint of 0.3 dB. For fast motion sequences, "Dancer," "Foreman," and "Flower," the proposed algorithm can adaptively select low subsample ratio based on their high degree of high-frequency characteristic and visual quality degradation is 0.08 dB at most. Other video sequences are distributed among 16 : 4 and 16 : 2 subsample because low degree of high frequency. Figure 11 shows the PSNR value of each frame for "Table" sequence and the PSNRY results of the proposed algorithm is also very close to the PSNRY results of fixed 16 : 16 subsample ratio. Finally, the results of speedup ratio is shown in Table 8. From Table 8, the speedup ratio can efficiently achieve between 1.056 and 5.428 and operation timing of motion estimation can be more less than FSBM because of less search points. The average speedup ratio is 2.64. Therefore, FME algorithm which combines with the proposed algorithm is a better methodology of motion estimation in H.264/AVC under maintaining the stable visual quality and power-saving for all video sequences.
PSNRY versus subsample ratio based on Table 7 and shows that all tested sequences can satisfy to maintain the visual quality degradation under constraint of 0.3 dB. For fast motion sequences, "Dancer," "Foreman," and "Flower," the proposed algorithm can adaptively select low subsample ratio based on their high degree of high-frequency characteristic and visual quality degradation is 0.08 dB at most. Other video sequences are distributed among 16 : 4 and 16 : 2 subsample because low degree of high frequency. Figure 11 shows the PSNR value of each frame for "Table" sequence and the PSNRY results of the proposed algorithm is also very close to the PSNRY results of fixed 16 : 16 subsample ratio. Finally, the results of speedup ratio is shown in Table 8. From Table 8, the speedup ratio can efficiently achieve between 1.056 and 5.428 and operation timing of motion estimation can be more less than FSBM because of less search points. The average speedup ratio is 2.64. Therefore, FME algorithm which combines with the proposed algorithm is a better methodology of motion estimation in H.264/AVC under maintaining the stable visual quality and power-saving for all video sequences.
6. Conclusion
In this paper, we present a quality-stationary ME that is aware of content motion. By setting the subsample ratio according to the motion-level, the proposed algorithm can have the quality degradation low all over the video frames and require low computation load. As shown in the experimental results, with the optimal threshold values, the algorithm can make the quality degradation less than 0.36 dB while saving 69.6% ( )) power consumption for FSBM. For the application of FBMA, the quality is stationary with the degradation of 0.27 dB and the power consumption is reduced by the factor of 62.2% (
)) power consumption for FSBM. For the application of FBMA, the quality is stationary with the degradation of 0.27 dB and the power consumption is reduced by the factor of 62.2% ( )). The estimation of power consumption reduction is referred to the average subsampling ratio in that the power consumption should be proportional to the subsampling amount. The higher the subsampling amount, the more the power consumption. One can also adjust the size of search range or calculation precision for achieving the quality-stationary. However, either approach cannot have high degree of flexibility for hardware implementation.
)). The estimation of power consumption reduction is referred to the average subsampling ratio in that the power consumption should be proportional to the subsampling amount. The higher the subsampling amount, the more the power consumption. One can also adjust the size of search range or calculation precision for achieving the quality-stationary. However, either approach cannot have high degree of flexibility for hardware implementation.
References
ISO/IEC CD 11172-2(MPEG-1 Video) : Information technology-coding of moving pictures and asociated audio for digitsl storage media at up about 1.5 Mbits/s: Video. 1993.
ISO/IEC CD 13818-2–ITU-T H.262(MPEG-2 Video) : Information technology-generic coding of moving pictures and asociated audio information: Video. 1995.
ISO/IEC 14496-2 (MPEG-4 Video) : Information Technology-Generic Coding of Audio-Visual Objects. Part2:Visual, 1999
Wiegand T, Sullivan GJ, Luthra A: Draft ITU-T Recommendation H.264 and Final Draft International Standard 14496-10 AVC. VT of ISO/IEC JTC1/SC29/WG11 and ITU-T SG16/Q.6, Doc. JVT-G050r1, Geneva, Switzerland, May 2003
Richardson I: H.264 and MPEG-4 Video Compression. John Wiley & Sons, New York, NY, USA; 2003.
Wiegand T, Sullivan GJ, Bjøntegaard G, Luthra A: Overview of the H.264/AVC video coding standard. IEEE Transactions on Circuits and Systems for Video Technology 2003, 13(7):560-576.
Kuhn P: Algorithm, Complexity Analysis and VLSI Architecture for MPEG-4 Motion Estimation. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1999.
Do VL, Yun KY: A low-power VLSI architecture for full-search block-matching motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 1998, 8(4):393-398. 10.1109/76.709406
Shen J-F, Wang T-C, Chen L-G: A novel low-power full-search block-matching motion-estimation design for H.263+. IEEE Transactions on Circuits and Systems for Video Technology 2001, 11(7):890-897. 10.1109/76.931116
Brünig M, Niehsen W: Fast full-search block matching. IEEE Transactions on Circuits and Systems for Video Technology 2001, 11(2):241-247. 10.1109/76.905989
Sousa L, Roma N: Low-power array architectures for motion estimation. Proceedings of the 3rd IEEE Workshop on Multimedia Signal Processing, 1999 679-684.
Jain JR, Jain AK: Displacement measurement and its application in interframe image coding. IEEE Transactions on Communications 1981, 29(12):1799-1808. 10.1109/TCOM.1981.1094950
Ogura E, Ikenaga Y, Iida Y, Hosoya Y, Takashima M, Yamashita K: Cost effective motion estimation processor LSI using a simple and efficient algorithm. IEEE Transactions on Consumer Electronics 1995, 41(3):690-698. 10.1109/30.468021
Mietens S, De With PHN, Hentschel C: Computational-complexity scalable motion estimation for mobile MPEG encoding. IEEE Transactions on Consumer Electronics 2004, 50(1):281-291. 10.1109/TCE.2004.1277875
Chen M, Chen L, Chiueh T: One-dimensional full search motion estimation algorithm for video coding. IEEE Transactions on Circuits and Systems for Video Technology 1994, 4(5):504-509. 10.1109/76.322998
Li R, Zeng B, Liou ML: A new three-step search algorithm for block motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 1994, 4(4):438-442. 10.1109/76.313138
Tham JY, Ranganath S, Ranganath M, Kassim AA: A novel unrestricted center-biased diamond search algorithm for block motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 1998, 8(4):369-377. 10.1109/76.709403
Zhu C, Lin X, Chau L-P: Hexagon-based search pattern for fast block motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2002, 12(5):349-355. 10.1109/TCSVT.2002.1003474
Kim KB, Jeon YG, Hong M-C: Variable step search fast motion estimation for H.264/AVC video coder. IEEE Transactions on Consumer Electronics 2008, 54(3):1281-1286.
Sarwer MG, Wu QMJ: Adaptive variable block-size early motion estimation termination algorithm for H.264/AVC video coding standard. IEEE Transactions on Circuits and Systems for Video Technology 2009, 19(8):1196-1201.
Chen Z, Xu J, He Y, Zheng J: Fast integer-pel and fractional-pel motion estimation for H.264/AVC. Journal of Visual Communication and Image Representation 2006, 17(2):264-290. 10.1016/j.jvcir.2004.12.002
Cai C, Zeng H, Mitra SK: Fast motion estimation for H.264. Signal Processing: Image Communication 2009, 24(8):630-636. 10.1016/j.image.2009.02.012
Li W, Salari E: Successive elimination algorithm for motion estimation. IEEE Transactions on Image Processing 1995, 4(1):105-107. 10.1109/83.350809
Luo J-H, Wang C-N, Chiang T: A novel all-binary motion estimation (ABME) with optimized hardware architectures. IEEE Transactions on Circuits and Systems for Video Technology 2002, 12(8):700-712. 10.1109/TCSVT.2002.800859
Kim N-J, Ertürk S, Lee H-J: Two-bit transform based block motion estimation using second derivatives. IEEE Transactions on Consumer Electronics 2009, 55(2):902-910.
Lee S, Chae S-I: Motion estimation algorithm using low resolution quantisation. Electronics Letters 1996, 32(7):647-648. 10.1049/el:19960420
Cheng HW, Dung LR: EFBLA: a two-phase matching algorithm for fast motion estimation. Proceedings of the 3rd IEEE Pacific Rim Conference on Multimedia: Advances in Multimedia Information Processing, December 2002 2532: 112-119.
Su C-L, Jen C-W: Motion estimation using MSD-first processing. IEE Proceedings: Circuits, Devices and Systems 2003, 150(2):124-133. 10.1049/ip-cds:20030332
Huang S-Y, Cho C-Y, Wang J-S: Adaptive fast block-matching algorithm by switching search patterns for sequences with wide-range motion content. IEEE Transactions on Circuits and Systems for Video Technology 2005, 15(11):1373-1384.
Ng K-H, Po L-M, Wong K-M, Ting C-W, Cheung K-W: A search patterns switching algorithm for block motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2009, 19(5):753-759.
Nie Y, Ma K-K: Adaptive irregular pattern search with matching prejudgment for fast block-matching motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2005, 15(6):789-794.
Lim J-H, Choi H-W: Adaptive motion estimation algorithm using spatial and temporal correlation. Proceedings of the IEEE Pacific Rim Conference on Communications, Computers and Signal Processing (PACRIM '01), August 2001, Victoria, Canada 2: 473-476.
Liu B, Zaccarin A: New fast algorithms for the estimation of block motion vectors. IEEE Transactions on Circuits and Systems for Video Technology 1993, 3(2):148-157. 10.1109/76.212720
Cheung C, Po L: A hierarchical block motion estimation algorithm using partial distortion measure. Proceedings of the International Conference on Image Processing (ICIP '97), October 1997 3: 606-609.
Cheung C-K, Po L-M: Normalized partial distortion search algorithm for block motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2000, 10(3):417-422. 10.1109/76.836286
Wang C-N, Yang S-W, Liu C-M, Chiang T:A hierarchical decimation lattice based on
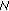 -queen with an application for motion estimation. IEEE Signal Processing Letters 2003, 10(8):228-231. 10.1109/LSP.2003.814403
-queen with an application for motion estimation. IEEE Signal Processing Letters 2003, 10(8):228-231. 10.1109/LSP.2003.814403Wang C-N, Yang S-W, Liu C-M, Chiang T:A hierarchical
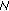 -queen decimation lattice and hardware architecture for motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2004, 14(4):429-440. 10.1109/TCSVT.2004.825550
-queen decimation lattice and hardware architecture for motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2004, 14(4):429-440. 10.1109/TCSVT.2004.825550Cheng H-W, Dung L-R: A vario-power ME architecture using content-based subsample algorithm. IEEE Transactions on Consumer Electronics 2004, 50(1):349-354. 10.1109/TCE.2004.1277884
Chan Y-L, Siu W-C: New adaptive pixel decimation for block motion vector estimation. IEEE Transactions on Circuits and Systems for Video Technology 1996, 6(1):113-118. 10.1109/76.486426
Wang YK, Wang YQ, Kuroda H: A globally adaptive pixel-decimation algorithm for block-motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2000, 10(6):1006-1011. 10.1109/76.867940
Oppenheim AV, Schafer RW, Buck JR: Discrete-Time Signal Processing. Prentice-Hall, Upper Saddle River, NJ, USA; 1999.
Chan Y-L, Siu W-C: New adaptive pixel decimation for block motion vector estimation. IEEE Transactions on Circuits and Systems for Video Technology 1996, 6(1):113-118. 10.1109/76.486426
Wang Y, Wang Y, Kuroda H: A globally adaptive pixel-decimation algorithm for block-motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2000, 10(6):1006-1011. 10.1109/76.867940
Dung L-R, Lin M-C: Wide-range motion estimation architecture with dual search windows for high resolution video coding. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences 2008, E91-A(12):3638-3650. 10.1093/ietfec/e91-a.12.3638
Joint Video Team : Reference Software JM10.2. http://iphome.hhi.de/suehring/tml/download/old_jm/
Acknowledgment
This work was supported in part by the National Science Council, R.O.C., under the grant number NSC 95-2221-E-009-337-MY3.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lin, MC., Dung, LR. A Content-Motion-Aware Motion Estimation for Quality-Stationary Video Coding. EURASIP J. Adv. Signal Process. 2010, 403634 (2010). https://doi.org/10.1155/2010/403634
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/403634



 Q with 16 : 8, 16 : 4, 16 : 2 subsample ratios for table sequence.
Q with 16 : 8, 16 : 4, 16 : 2 subsample ratios for table sequence.








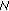 -queen with an application for motion estimation. IEEE Signal Processing Letters 2003, 10(8):228-231. 10.1109/LSP.2003.814403
-queen with an application for motion estimation. IEEE Signal Processing Letters 2003, 10(8):228-231. 10.1109/LSP.2003.814403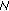 -queen decimation lattice and hardware architecture for motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2004, 14(4):429-440. 10.1109/TCSVT.2004.825550
-queen decimation lattice and hardware architecture for motion estimation. IEEE Transactions on Circuits and Systems for Video Technology 2004, 14(4):429-440. 10.1109/TCSVT.2004.825550