- Research Article
- Open access
- Published:
Multifrequency and Multistatic Inverse Synthetic Aperture Radar, with Application to FM Passive Radar
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 497074 (2009)
Abstract
This paper deals with the imaging of a moving target using a multifrequency and multistatic radar consisting in one receiver and several narrowband transmitters. Considering two hypotheses about the studied target, we derive two multistatic inverse synthetic aperture radar processors: the first one, which models the target as a set of isotropic points, performs a coherent sum of bistatic images; the second one, which models the target as a set of nonisotropic points, performs an incoherent sum of bistatic images. Numerical simulations are done, which demonstrate the efficiency of the second processor. We also apply both processors to a multistatic passive radar scenario for which the transmitters are FM stations located in a realistic configuration. We study the system performance in terms of resolution and sidelobe levels as a function of the number of transmitters and of the integration time. Both processors are applied to similar complex targets for which the scattered fields are simulated by a numerical electromagnetic code. The resulting multistatic radar images show interesting characteristics that might be used by classification algorithms in future work.
1. Introduction
Passive radars use one or several transmitters of opportunity to detect, locate, and classify targets. This technique is cost effective because users only need to install receivers. Nevertheless, the use of civil communication signals, which are often narrowband signals, makes the detection and the classification difficult. The main limitations of passive radars are due to the center frequency and the bandwidth of these signals. For instance, for FM and TV signals, the center frequency varies from 100 MHz (for FM) to 800 MHz (for some TV stations in France) with bandwidths ranging from 75 kHz (for FM) to 1 MHz (for TV stations). For comparison, the center frequency and the bandwidth of a monostatic active radar such as the RAMSES ONERA SAR system [1] in the X-band are approximately 10 GHz and 1.2 GHz. For reaching equivalent performances (resolution and sidelobe levels) as an active system, a passive radar has to illuminate the target a long time and to consider several narrowband transmitters (FM or TV) in order to compensate for the low values of the center frequency and the bandwidth. In the following, such a radar system will be called a multifrequency and multistatic radar.
Passive bistatic radar systems consisting in one transmitter and one receiver located at different places and using FM [2] and TV signals [3] have demonstrated the feasibility of passive radars. Detection, localization, and tracking algorithms have been developed and validated using real data. However, classification is better performed using multiple transmitters or receivers. Therefore, different approaches have recently been developed. An approach to Automatic Target Recognition (ATR) consists in comparing the modeled Radar Cross Section (RCS) of different targets with those measured by the multistatic radar system [4–7]. Another approach, which is the one this paper focuses on, relies on the development of classification algorithms based on a target image obtained from the multistatic radar measurements.
In previous works [8, 9], we studied the resolution attainable by a multifrequency and multistatic radar using analytical and numerical approaches. Results showed that multifrequency and multistatic radars could achieve sufficient resolution using several narrowband transmitters and a long integration time. In this paper, we propose imaging algorithms for multifrequency and multistatic radars, which could be useful as a preprocessing for classification methods. Most of imaging algorithms are based on the Synthetic Aperture Radar (SAR) concept [10]. The main purpose of imaging algorithms is to achieve enough resolution to make the classification step easy. For instance, the final images corresponding to two similar targets must exhibit enough differences so that it is possible to make the difference. For narrowband radar, it is well known that data from transmitter-receiver pairs distributed all around the target allow to have an image [11, 12] with such properties. These particular systems are similar to tomographic ones. Recently, Wu and Munson [13] simulated the imaging of a moving airplane using a multistatic radar composed of several TV transmitters and a single receiver. The imaging algorithm in [13] relies on the assumption that the target is composed of isotropic points and uses 2D interpolation on the frequency domain to achieve the processing. However, the resulting images are subject to degradation because the target has to be illuminated over a long period (in this case, the target is often nonstationary). Several methods have been proposed for solving this problem: time-frequency-based methods [14–16], deconvolution methods [17], or optimization techniques [18].
This paper proposes new Multistatic Inverse SAR (MISAR) processors where SAR processors were showed to be particular cases of detection algorithms [19, 20]. Two MISAR processors are developed, depending on the hypotheses made about the target: in the first case the target is assumed to be equivalent to a set of isotropic points, and in the second case the target is assumed to be equivalent to a set of nonisotropic points. We demonstrate that the first processor is equivalent to the one proposed in [13] while the second one is slightly different.
Next, we apply both MISAR processors to a realistic multistatic FM passive radar configuration for which the FM transmitter locations are chosen according to those of the FM transmitters in France [21]. A study of image resolution based on methods presented in [8, 9] is performed as a function of the number of transmitters and of the integration time. Both MISAR processors are tested on two similar complex targets presented in [22]. This paper does not consider the estimation of the trajectory. This problem is addressed with an extended Kalman Filter or a particle filter in [2, 3, 7, 23–26].
Section 2 describes the hypotheses that are made about the target as well as the notations that will be used in this paper. Section 3 develops both MISAR processors and illustrates their potential via a numerical simulation. Section 4 details the geometric configuration of our multistatic passive FM radar scenario and presents the resulting image.
2. Problem Statement
We first present the notation needed to derive the desired detection algorithms. We next present two conjectures: the scattered field of target is either a set of isotropic points or a set of nonisotropic points. The corresponding detection problems are finally presented.
2.1. Context and Notation
Consider  narrowband transmitters (FM, TV,
narrowband transmitters (FM, TV,  ), each of them transmitting a continuous signal
), each of them transmitting a continuous signal  where
where  denotes the transmitter index (
denotes the transmitter index ( ).
).  is the center frequency of the transmitted signal and
is the center frequency of the transmitted signal and  is the baseband signal. Let
is the baseband signal. Let  be the cartesian coordinates of the transmitters as shown in Figure 1. The receiver, which is located at position
be the cartesian coordinates of the transmitters as shown in Figure 1. The receiver, which is located at position  , collects the reflected signals and performs
, collects the reflected signals and performs  complex demodulations with respect to
complex demodulations with respect to  . The direct path signals from each transmitter are assumed to have been removed by appropriate processing. The sampling period is denoted by
. The direct path signals from each transmitter are assumed to have been removed by appropriate processing. The sampling period is denoted by  , and the receiver collects
, and the receiver collects  samples from each transmitter. Signals
samples from each transmitter. Signals  are assumed normalized according to
are assumed normalized according to  . It is also assumed that only a single target is present, flying along a known trajectory which is considered to be along the
. It is also assumed that only a single target is present, flying along a known trajectory which is considered to be along the  -axis at height
-axis at height  with a constant velocity
with a constant velocity  . We consider a receiver such that its aperture enables the target detection located between
. We consider a receiver such that its aperture enables the target detection located between  and
and  . A moving coordinate system
. A moving coordinate system  , with origin
, with origin  , is used for the target point coordinates
, is used for the target point coordinates  , where
, where  =
=  . For clarity, only 2D imagery is considered.
. For clarity, only 2D imagery is considered.
2.2. Target Hypotheses
In this paper, we consider narrowband transmitters. As a consequence, the scattering function of the general target, which is denoted by  , can be assumed to be independent of the transmitted frequency. Moreover, assuming that the target can be described as a set of points,
, can be assumed to be independent of the transmitted frequency. Moreover, assuming that the target can be described as a set of points,

where  is the number of scattering points of the target,
is the number of scattering points of the target,  are the scalar coordinates of these points, and
are the scalar coordinates of these points, and  are the incident and observed angles defined in Figure 2. Since angles
are the incident and observed angles defined in Figure 2. Since angles  vary as a function of the target position and the transmitter number (indexed by
vary as a function of the target position and the transmitter number (indexed by  ), the scattering coefficient
), the scattering coefficient  is, without additional assumptions, a function of
is, without additional assumptions, a function of  (target position) and
(target position) and  (transmitter number). In this paper with a view to develop our MISAR processors, the scattering coefficient
(transmitter number). In this paper with a view to develop our MISAR processors, the scattering coefficient  is assumed to be independent of
is assumed to be independent of  .
.
Given this initial hypothesis, we consider two cases:
-
(i)
the isotropic case for which the scattering coefficient
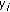 neither depends on the transmitter nor depends on the receiver location; in this case, the target can be considered to be a set of isotropic points;
neither depends on the transmitter nor depends on the receiver location; in this case, the target can be considered to be a set of isotropic points; -
(ii)
the nonisotropic case for which the scattering coefficient
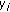 depends on the transmitter and receiver locations (indexed by
depends on the transmitter and receiver locations (indexed by  ); in this case, the
); in this case, the 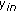 coefficients of each transmitter
coefficients of each transmitter  are different and the target is considered as a set of nonisotropic points.
are different and the target is considered as a set of nonisotropic points.
In the following, we denote by  the scattered field of the isotropic point located at pixel
the scattered field of the isotropic point located at pixel  and by
and by  the scattered field seen by transmitter
the scattered field seen by transmitter  of the nonisotropic point located at pixel
of the nonisotropic point located at pixel  .
.
2.3. Detection Problem for the Isotropic Case
We consider the following detection problem for the pixel at  ; the received signal may be composed either of noise (hypothesis
; the received signal may be composed either of noise (hypothesis  ) or of noise plus the reflected target signal (hypothesis
) or of noise plus the reflected target signal (hypothesis  ):
):

where  is the signal received from transmitter
is the signal received from transmitter  ,
,  is complex zero mean Gaussian noise with known variance
is complex zero mean Gaussian noise with known variance  , and
, and  is the noiseless signal reflected by a normalized isotropic point, originating from the transmitter
is the noiseless signal reflected by a normalized isotropic point, originating from the transmitter  . The expression for
. The expression for  is
is

where  is the time delay along the transmitter
is the time delay along the transmitter  -target-receiver path. The scattering coefficient
-target-receiver path. The scattering coefficient  is unknown.
is unknown.
Define the vectors  =
=  ,
,  =
=  ,
,  =
=  (where
(where  is the symbol for the transpose operation), and
is the symbol for the transpose operation), and

The initial detection problem (2) may be rewritten as

where  is unknown.
is unknown.
2.4. Detection Problem for the Nonisotropic Case
We consider the following detection problem for the pixel at  , where the received signal may be composed either of noise (hypothesis
, where the received signal may be composed either of noise (hypothesis  ) or of noise plus the reflected target signals (hypothesis
) or of noise plus the reflected target signals (hypothesis  ):
):

where the definitions of  ,
,  , and
, and  are the same as those of Section 2.3. The scattering coefficients
are the same as those of Section 2.3. The scattering coefficients  are unknown.
are unknown.
For the nonisotropic case,  is defined as follows:
is defined as follows:

The initial detection problem (6) may be rewritten as

where  are unknown.
are unknown.
3. Multistatic ISAR Processors
Both the isotropic (5) and the nonisotropic (8) detection problems described above are addressed in Sections 3.1 and 3.2. Moreover, simulations of the two resulting MISAR processors are provided and analyzed in Section 3.3.
3.1. MISAR Processor for Isotropic Case
The Generalized Likelihood Ratio Test for the detection problem (5) leads to

where  is the probability density function of vector
is the probability density function of vector  under the hypothesis
under the hypothesis  . The threshold
. The threshold  is usually adjusted to fulfill a given probability of false alarm. In Gaussian context, the above test may be rewritten as
is usually adjusted to fulfill a given probability of false alarm. In Gaussian context, the above test may be rewritten as

Estimation of  consists in determining
consists in determining

which leads to the least-squares solution

where  denotes the conjugate transpose operation. Substituting
denotes the conjugate transpose operation. Substituting  into (10),
into (10),

We propose to compose the target image  by plotting the test value of (13) for every
by plotting the test value of (13) for every  position:
position:

Let  denote the bistatic complex image created using only the transmitter
denote the bistatic complex image created using only the transmitter  . It is to be noted that (14) makes a coherent sum of every bistatic complex image which is identical to classic multistatic algorithms [13]. We call this algorithm Multistatic Coherent ISAR (MCISAR) processing.
. It is to be noted that (14) makes a coherent sum of every bistatic complex image which is identical to classic multistatic algorithms [13]. We call this algorithm Multistatic Coherent ISAR (MCISAR) processing.
The computation cost of the bistatic complex image  can prove to be heave. Nevertheless, an approximation such as the bistatic PFA proposed in [27] could be used with a view to better computational efficiency.
can prove to be heave. Nevertheless, an approximation such as the bistatic PFA proposed in [27] could be used with a view to better computational efficiency.
3.2. MISAR Processor for Nonisotropic Case
The Generalized Likelihood Ratio Test for the detection problem (8) leads to

In Gaussian context, the above test may be rewritten as

Estimation of  consists in determining
consists in determining

which leads to the least-squares solution

Substituting  into (16),
into (16),

We propose to compose target image  by plotting the test value of (19) for every
by plotting the test value of (19) for every  position:
position:

Equation (20) is an incoherent sum of every bistatic complex image. This result is consistent with the fact that the scattering coefficients are assumed to be different for each transmitter. Equation (20) thus differs from MCISAR (14) and classic multistatic algorithms that usually perform a coherent sum of every bistatic complex image. Such a result emphasizes our interest in modeling the received signal more accurately. We call this algorithm Multistatic Incoherent ISAR (MIISAR) processing.
3.3. Qualitative Comparison of MCISAR and MIISAR
With a view to compare the MCISAR and MIISAR processing, we perform two simulations. The first one considers the target as an isotropic point, and the second one as a nonisotropic point, both located at the center of the mobile reference  . The radar configuration, for which four FM transmitters are used, is given in Figure 1. The parameters of the simulation are summarized in Table 1. The values of the scattering coefficients for the nonisotropic point have no particular physical meaning because they were randomly chosen. The target speed is 150 m/s. The synthetic array length is 5.25 km long, which corresponds to an integration time of 35 seconds. The receiver is located at (40,20) km. The positions of the transmitters and receiver, as well as the target trajectory, are also shown in Figure 3.
. The radar configuration, for which four FM transmitters are used, is given in Figure 1. The parameters of the simulation are summarized in Table 1. The values of the scattering coefficients for the nonisotropic point have no particular physical meaning because they were randomly chosen. The target speed is 150 m/s. The synthetic array length is 5.25 km long, which corresponds to an integration time of 35 seconds. The receiver is located at (40,20) km. The positions of the transmitters and receiver, as well as the target trajectory, are also shown in Figure 3.
Results of MCISAR and MIISAR considering both the isotropic and the nonisotropic points are displayed in Figure 4. Regarding the isotropic point, it is to be noted that the MIISAR result is the envelope of the MCISAR one. However, an important drawback of the MCISAR method should be pointed out for the nonisotropic point case: there are two principal lobes for only one point. On the other hand, the MIISAR result for the isotropic point is similar to that corresponding to the nonisotropic point. Such simulation results enable the use of MIISAR processing to be envisaged for target recognition.
In the next section a quantitative study of both MISAR processors is performed. Resolution and sidelobe levels are studied in a realistic ISAR context and the MCISAR and MIISAR processors are applied to complex targets.
4. Simulations with FM Passive Multistatic Radar
The first subsection describes the FM passive radar configuration and the considered targets. The second subsection is dedicated to the study of the impact of the system geometry on the image resolution for the MIISAR. Finally, in the third subsection, the MCISAR and MIISAR processors are applied to complex targets and the results are analyzed.
4.1. Simulation Context
As a realistic ISAR context configuration, which is shown in Figure 5, we chose transmitter locations corresponding to the FM transmitters that exist near Gueret (a small city in the center of France) where up to 103 transmitters are available in a 100 km side square [21]. For the sake of illustration, the transmitters are assumed to provide sufficient Signal-to-Noise Ratio (SNR) so that the target is visible to all of them. However, in practice such a case is unlikely to happen. The receiver is located at coordinates  km in the
km in the  plane. The height of the target flight
plane. The height of the target flight  is 100 meters.
is 100 meters.
The center frequencies of each of the  narrowband transmitters are all different and are separated by at least
narrowband transmitters are all different and are separated by at least  kHz. We assume that the center frequency
kHz. We assume that the center frequency  for transmitter
for transmitter  is equal to
is equal to  MHz. This choice was made so as to have the total frequency coverage in the FM band and therefore to obtain the best image resolution in the chosen geometric configuration.
MHz. This choice was made so as to have the total frequency coverage in the FM band and therefore to obtain the best image resolution in the chosen geometric configuration.
The FM signal for each transmitter is assumed to carry "rock music" in order to cover a maximum bandwidth. The music signal is frequency modulated according to the commercial FM standard [24]. An example of the transmitted baseband signal spectrum normalized with respect to its maximum is shown in Figure 6. Notice that the signal power is not constant over the frequency band and that the bandwidth could be considered as quite small. The duration of the received signal depends on the Synthetic Array Length (SAL) and the speed of the target. The baseband signals are sampled at  kHz.
kHz.
To study the impact of the geometric configuration of Figure 5 on resolution, Section 4.2 considers the target to be an isotropic point. Section 4.3 considers the two complex targets presented in [22]: a "cycone" and an airplane, shown in Figure 7. Both are 10.5 m long. The width of the airplane is 6 m. Figure 8 shows the target position in the moving coordinate system  . The scattered fields of both targets in copolarizations and cross polarizations are computed from numerical code presented in [22]. We notice that the scattered fields of both targets could not be considered as a simple sum of point scatterers (isotropic or nonisotropic). Therefore, the first hypothesis of Section 2.2 is not ensured: the scattered fields of both targets vary as a function of the target position (indexed by
. The scattered fields of both targets in copolarizations and cross polarizations are computed from numerical code presented in [22]. We notice that the scattered fields of both targets could not be considered as a simple sum of point scatterers (isotropic or nonisotropic). Therefore, the first hypothesis of Section 2.2 is not ensured: the scattered fields of both targets vary as a function of the target position (indexed by  ). This configuration allows us to test the performance and the robustness of our MISAR processors in a realistic configuration in terms of frequencies, transmitter locations, integration time, and complex targets.
). This configuration allows us to test the performance and the robustness of our MISAR processors in a realistic configuration in terms of frequencies, transmitter locations, integration time, and complex targets.
4.2. Study of the Impact of the Geometric Configuration on Image Resolutions
In this subsection, we focus on the final image resolution and sidelobe levels that could be obtained by the MIISAR processor in the configuration of Figure 5. The MIISAR processor is chosen because its result corresponds to the envelope of the MCISAR one. Therefore, the impact of parameters, such as the integration time and the number of transmitters, on resolution and sidelobe levels is obviously the same for both processors.
Our resolution study is similar to the one reported in [8, 9]. First, let the target be an isotropic point located at coordinate  . The result for this target and for a given configuration is obtained by the MIISAR processor. An ellipse is obtained from this image by computing the image level at the maximum minus 3 dB. Several parameters, defined in Figure 10, are determined from this ellipse to measure the quality of the image resolution: the area of the ellipse in
. The result for this target and for a given configuration is obtained by the MIISAR processor. An ellipse is obtained from this image by computing the image level at the maximum minus 3 dB. Several parameters, defined in Figure 10, are determined from this ellipse to measure the quality of the image resolution: the area of the ellipse in  , and the maximal and minimal resolution in
, and the maximal and minimal resolution in  (the large and small axes of the ellipse).
(the large and small axes of the ellipse).
To study sidelobe levels, the following parameter, denoted the Mean Absolute Error (MAE), is used:

where  and
and  are the number of pixels of the image and
are the number of pixels of the image and  is a reference image, which is assumed of high quality in terms of resolution and sidelobe levels.
is a reference image, which is assumed of high quality in terms of resolution and sidelobe levels.
The reference image is obtained with a Synthetic Array Length (SAL) of 48 km and all 103 transmitters. This image is shown in Figure 9. Image resolution is quite good, with values of about 1 m. Moreover, we believe that the sidelobe levels are sufficient for imaging of both targets of Figure 7.
Now, we describe all cases tested as a function of the  and
and  from the geometric configuration of Figure 5.
from the geometric configuration of Figure 5.
Case 1.
SAL = 4 km and  transmitters.
transmitters.
Case 2.
SAL = 8 km and  transmitters.
transmitters.
Case 3.
SAL = 16 km and  transmitters.
transmitters.
Case 4.
SAL = 32 km and  transmitters.
transmitters.
Case 5.
SAL = 32 km and  transmitters, with a frequency spacing of 200 kHz.
transmitters, with a frequency spacing of 200 kHz.
Case 6.
SAL  km and
km and  transmitters, with a frequency spacing of 800 kHz.
transmitters, with a frequency spacing of 800 kHz.
Resulting image resolutions and MAE calculations (for the study of the sidelobe levels) are summarized in Table 2.
It is first to be noted that relatively good image resolution is obtained with a small SAL when all transmitters are considered. This might mislead us into thinking that a small SAL is sufficient to obtain usable images of complex targets. Unfortunately, the sidelobe levels are high for these cases, as indicated by the MAE value. The MAE decreases as the SAL increases, which is reasonable. In particular, the result for an SAL of 32 km and 103 transmitters seems promising in terms of resolution and sidelobe levels. However, we are interested in reducing the number of transmitters to reach a less complex radar system; also, it is unlikely that so many transmitters could be used in practice.
Therefore, let us consider less transmitters. To better comprehend the results of Cases 4–6 in Table 2, Figure 11 shows the corresponding Fourier coverage (see [8, 9] for more details) of the images obtained with the MIISAR processor. The best case, which best fills the Fourier plane, is reached when all of the 103 transmitters are considered. When only 25 transmitters with a frequency spacing of 200 kHz are considered, the resolution performance is strongly degraded (1.2 m to 3 m for the maximal resolution). We notice that the Fourier plane does not cover the same area as in Case 4 (with 103 transmitters). In our geometric configuration, image resolution is influenced by the total frequency spacing provided by the considered transmitters. This value is identical in Cases 4 and 6 ( kHz
kHz  kHz), and therefore the image resolutions are similar. Nevertheless, the MAE (linked to sidelobe levels) is slightly lower (
kHz), and therefore the image resolutions are similar. Nevertheless, the MAE (linked to sidelobe levels) is slightly lower ( 30.8 dB against
30.8 dB against  32.1 dB) because the center of the Fourier plane is less filled in Case 6 than in Case 4. But, this value is more important in Case 6 than in Case 5 (
32.1 dB) because the center of the Fourier plane is less filled in Case 6 than in Case 4. But, this value is more important in Case 6 than in Case 5 ( 30.8 dB against
30.8 dB against  27.1 dB).
27.1 dB).
To conclude, Case 6 provides results close the reference, but with lower complexity. Figure 12 shows the image of an isotropic point in this case. This image is close to the reference, shown in Figure 9. In the following, we choose this Radar configuration: SAL equal to 32 km and 25 transmitters with a frequency spacing of 800 kHz.
4.3. Simulation Results
In this subsection, we apply the MCISAR and MIISAR processors within the simulation context of Section 4.1. In this discussion, copolarization refers to  polarization and cross polarization refers to
polarization and cross polarization refers to  polarization.
polarization.
In a first simulation, we present bistatic images of the "cycone" and of the airplane obtained considering one transmitter and one receiver. For simulation, it is the transmitter operating at the highest center frequency that is chosen. The SAL is 32 km. The result in copolarization for both targets is shown in Figure 13. From such results, the determination of the characteristics of the targets (length and width) is not trivial. Nevertheless, both images exhibit slight differences although the target shapes are similar. Indeed, energy in the airplane image is more concentrated. This allows us to expect interesting results in the multistatic context.
In a second simulation, the multistatic context is considered. The configuration that is taken is the one described in Section 4.2 for which the SAL is 32 km and 25 transmitters with a frequency spacing of 800 kHz are used. Figure 14 shows the results of MCISAR and MIISAR processors for the "cycone" and for the airplane for copolarization. Both the processors enable to determine some target characteristics along the  -axis, such as the length (in the order of 10 m) and the position of the back (located at
-axis, such as the length (in the order of 10 m) and the position of the back (located at  =
=  m). However, the width of the cylinder can only be measured with the MCISAR processor (in the order of 2 m). The airplane and "cycone" images resulting from the MCISAR processor are similar. On the contrary, the airplane and the "cycone" images created by the MIISAR processor appear to be different; the energy maximum is concentrated in the back of the airplane and a wing seems visible at position
m). However, the width of the cylinder can only be measured with the MCISAR processor (in the order of 2 m). The airplane and "cycone" images resulting from the MCISAR processor are similar. On the contrary, the airplane and the "cycone" images created by the MIISAR processor appear to be different; the energy maximum is concentrated in the back of the airplane and a wing seems visible at position  m. Both processors seem capable of determining basic target parameters like length, width, and so forth, but only the MIISAR processor gives two images with enough difference to make the difference between the two targets.
m. Both processors seem capable of determining basic target parameters like length, width, and so forth, but only the MIISAR processor gives two images with enough difference to make the difference between the two targets.
Figure 15 shows results of MCISAR and MIISAR processors for the "cycone" and the airplane for cross-polarization. The energy in the airplane image is 20 dB higher than the energy for the "cycone" one. In particular, the energy in the "cycone" image is too weak to enable the results to be interpreted. For the airplane, the MIISAR result seems more interesting than the MCISAR result; the energy is higher and the phenomenon that creates the cross-polarization response is well localized near the back and the beginning of the wings.
These results show that both processors applied to copolarization and cross-polarization data might help developing classification rules. Moreover, the processors appear to be robust with respect to violations of the hypotheses they were derived under.
5. Conclusion
This paper developed Multistatic ISAR processors from a detection theory viewpoint. From two hypotheses about the considered target, we developed two MISAR processors.
-
(i)
The first processor, called MCISAR, is based on the isotropic point hypothesis. It is analogous to classical processors as it coherently sums bistatic images.
-
(ii)
The second processor, called MIISAR, assumes that the scattered field of the target is different for each narrowband transmitter (realistic hypothesis in our context). This processor incoherently sums bistatic images.
Numerical simulations have been done in order to qualitatively illustrate the potential of the MIISAR processor in cases where the isotropic point hypothesis is not respected.
The last section applied the two considered processors to two similar complex targets in a realistic multistatic FM passive radar scenario. A study of the resolution and sidelobe levels has shown that it is not necessary to take every transmitters into account to get an optimal result. However, using transmitters that provide with wide frequency spacing and a large SAL is needed to achieve decent results.
Copolarization results from the MCISAR processor allowed us to determine some simple parameters of both the considered targets, such as the length and the width of the cylinder; however, images of both targets were similar and the wings and the cone were not seen. The MIISAR processor is proved to be more performant for discriminating the two targets because the images provided in copolarization are different. Moreover, the cross-polarization images obtained by the MIISAR processor exhibited many differences. According to those results, the proposed imaging algorithms may be used as first steps of a classification process using multifrequency and multistatic passive radar.
Future work will deal with more complex target models and the development of associated imaging algorithms based on the monostatic SAR processors presented in [19, 20] where subspace approaches are used to integrate complex target model in monostatic SAR processing.
References
Cantalloube H, Dubois-Fernandez P: Airborne x-band sar imaging with 10 cm resolution: technical challenge and preliminary results. Proceedings of the 5th European Conference on Synthetic Aperture Radar (EUSAR '04), May 2004, Ulm, Germany
Howland PE, Maksimiuk D, Reitsma G: FM radio based bistatic radar. IEE Proceedings: Radar, Sonar and Navigation 2005, 152(3):107-115. 10.1049/ip-rsn:20045077
Howland PE: Target tracking using television-based bistatic radar. IEE Proceedings: Radar, Sonar and Navigation 1999, 146(3):166-174. 10.1049/ip-rsn:19990322
Ehrman L, Lanterman AD: Automated target recognition using passive radar and coordinated flight models. In Automatic Target Recognition XIII, April 2003, Orlando, Fla, USA, Proceedings of SPIE Edited by: Sadjadi FA. 5094: 196-207.
Ehrman LM, Lanterman AD: A robust algorithm for automatic target recognition using passive radar. Proceedings of the 36th IEEE Annual Southeastern Symposium on System Theory, March 2004, Atlanta, Ga, USA 102-106.
Ehrman LM, Lanterman AD: A robust algorithm for automated target recognition using precomputed radar cross sections. In Automatic Target Recognition XIV, April 2004, Orlando, Fla, USA, Proceedings of SPIE Edited by: Sadjadi FA. 5426: 197-208.
Herman SM: A particle filtering approach to joint passive radar tracking and target classification, Ph.D. thesis. University of Illinois, Urbana, Ill, USA; 2002.
Maussang F, Daout F, Ginolhac G, Schmitt F: Multistatic scenarios for a GPS SAR system. Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS '08), July 2008, Boston, Mass, USA 3: 270-273.
Daout F, Schmitt F, Ginolhac G: Performance analysis of a bistatic/multistatic passive sar system based on a GPS signal. submitted to IEEE Transactions on Geoscience and Remote Sensing
Soumekh M: Synthetic Aperture Radar Signal Processing. Wiley-Interscience, New York, NY, USA; 1999.
Mensa DL, Heidbreder GR: Bistatic synthetic-aperture radar imaging of rotating objects. IEEE Transactions on Aerospace and Electronic Systems 1982, 18(4):423-431.
Walker JL: Range-doppler imaging of rotating objects. IEEE Transactions on Aerospace and Electronic Systems 1980, 16(1):23-52.
Wu Y, Munson DC Jr.: Multistatic synthetic aperture imaging of aircraft using reflected television signals. In Algorithms for Synthetic Aperture Radar Imagery VIII, April 2001, Orlando, Fla, USA, Proceedings of SPIE Edited by: Zelnio EG. 4382: 1-12.
Wu Y, Munson DC Jr.: Wide-angle ISAR passive imaging using Smoothed Pseudo Wigner-Ville distribution. Proceedings of the IEEE National Radar Conference, May 2001, Atlanta, Ga, USA 363-368.
Wu Y, Munson DC Jr.: Multistatic passive radar imaging using the Smoothed Pseudo Wigner-Ville distribution. Proceedings of IEEE International Conference on Image Processing (ICIP '01), October 2001, Thessaloniki, Greece 3: 604-607.
Lanterman AD, Munson DC Jr., Wu Y: Wide-angle radar imaging using time-frequency distributions. IEE Proceedings: Radar, Sonar and Navigation 2003, 150(4):203-211. 10.1049/ip-rsn:20030712
Lanterman AD, Munson DC Jr.: Deconvolution techniques for passive radar imaging. In Algorithms for Synthetic Aperture Radar Imagery IX, April 2002, Orlando, Fla, USA, Proceedings of SPIE Edited by: Zelnio EG. 4727: 166-177.
Cetin M, Lanterman AD: Region-enhanced passive radar imaging. IEE Proceedings: Radar, Sonar and Navigation 2005, 152(3):185-194. 10.1049/ip-rsn:20045019
Durand R, Ginolhac G, Thirion L, Forster P: New SAR processor based on matched subspace detectors. IEEE Transactions on Aerospace and Electronic Systems 2009, 45(1):221-236.
Durand R, Ginolhac G, Thirion L, Forster P: SAR processor based on a CFAR signal or interference subspace detector matched to man made target detection in a forest. Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '07), April 2007, Honolulu, Hawaii, USA 2: 293-296.
Agence National des Fréquences : Emplacement des émetteurs fm en france. http://www.cartoradio.fr/netenmap.php?cmd=zoomfull
Daout F, Schmitt F, Ginolhac G: Computation of bistatic ser with nec2 in a context of passive isar system. Proceedings of IEEE Geoscience and Remote Sensing Symposium (IGARSS '05), July 2005, Seoul, South Korea
Petsios MN, Alivizatos EG, Uzunoglu NK: Manoeuvring target tracking using multiple bistatic range and range-rate measurements. Signal Processing 2007, 87(4):665-686. 10.1016/j.sigpro.2006.07.003
Forster P, Lesturgie M: Passive radar for target tracking and classification. Proceedings of the International Radar Conference, October 2004, Toulouse, France
Tobias M, Lanterman AD: Probability hypothesis density-based multitarget tracking with bistatic range and Doppler observations. IEE Proceedings: Radar, Sonar and Navigation 2005, 152(3):195-205. 10.1049/ip-rsn:20045031
Tobias M, Lanterman AD: Techniques for birth-particle placement in the probability hypothesis density particle filter applied to passive radar. IET Radar, Sonar and Navigation 2008, 2(5):351-365. 10.1049/iet-rsn:20070051
Rigling BD, Moses RL: Polar format algorithm for bistatic SAR. IEEE Transactions on Aerospace and Electronic Systems 2004, 40(4):1147-1159. 10.1109/TAES.2004.1386870
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ginolhac, G., Schmitt, F., Daout, F. et al. Multifrequency and Multistatic Inverse Synthetic Aperture Radar, with Application to FM Passive Radar. EURASIP J. Adv. Signal Process. 2010, 497074 (2009). https://doi.org/10.1155/2010/497074
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/497074


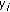 neither depends on the transmitter nor depends on the receiver location; in this case, the target can be considered to be a set of isotropic points;
neither depends on the transmitter nor depends on the receiver location; in this case, the target can be considered to be a set of isotropic points;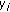 depends on the transmitter and receiver locations (indexed by
depends on the transmitter and receiver locations (indexed by  ); in this case, the
); in this case, the 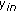 coefficients of each transmitter
coefficients of each transmitter  are different and the target is considered as a set of nonisotropic points.
are different and the target is considered as a set of nonisotropic points.





 .
.





