- Research Article
- Open access
- Published:
Uplink User Signal Separation for OFDMA-Based Cognitive Radios
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 502369 (2009)
Abstract
Spectrum awareness of orthogonal frequency division multiple access- (OFDMA-) based cognitive radios (CRs) can be improved by enabling them to separate the primary user signals in the uplink (UL). Assuming availability of information about the basic parameters of the primary system as well as time synchronization to the first arriving user signal, two algorithms are proposed in this paper. The first one targets estimating the size of the frequency allocation block of the primary system. The performance of this algorithm is compared with the results of a Gaussian approximation-based approach that aims to determine the probability of correct block size estimation theoretically. The second one is a semiblind user separation algorithm, which estimates the carrier frequency offsets and time delays of each block by exploiting the cross-correlations over pilot subcarriers. A two-dimensional clustering method is then employed to group the estimates, where each group belongs to a different user. It is shown that the proposed algorithms can improve the spectrum opportunity detection of cognitive radios. Feasibility of the algorithms is proved through practical simulations.
1. Introduction
Spectrum awareness is one of the fundamental features of cognitive radios (CRs) [1]. It has conventionally been considered a radio's being aware of the occupied and available frequency bands within its target spectrum [2]. It is achieved through spectrum sensing, where interference temperature is measured over the entire spectrum targeted, and the parts whose energy level exceeds a certain threshold are considered to be occupied [3, 4]. A different aspect was added to the spectrum awareness concept in [5] by attempting to characterize the source of the signal in the occupied spectrum. In this work, we propose to enhance the spectrum awareness by providing the cognitive radios with the capability of separating the primary user signals from each other in the uplink (UL). We consider orthogonal frequency division multiple access- (OFDMA-) based CR systems that coexist with a primary network that is also OFDMA-based. The proposed algorithm can be applicable to single carrier-frequency disivion multiple accessing- (SC-FDMA-) based UL systems, as well, given that the resource blocks employed enable estimation of user specific parameters.
Due to the involvement of multiple user signals, the uplink of OFDMA systems poses a number of challenges that do not exist in the downlink (DL). Most of these problems including multiuser channel estimation [6], carrier frequency offset (CFO) estimation [7], synchronization and symbol timing estimation [8, 9], multiuser interference cancellation [10], and subcarrier and power allocation [11] are investigated extensively in the prior art. However, the problem of separating UL user signals without access to the subcarrier assignment scheme (SAS) has not been investigated in detail in the literature.
A practical cognitive radio application where user separation might be quite useful is a cochannel femtocell network coexisting with a macrocell network [12, 13], both of which have an OFDMA-based physical layer. If the coexistence is based on a shared spectrum approach where the femtocell utilizes the available parts of the macrocell spectrum in an opportunistic manner, user separation can be very beneficial to the femtocell. How the user separation and block size estimation algorithms proposed in this paper that might improve the spectrum opportunity detection for femtocells is explained in Section 5. Other possible applications regarding femtocell-macrocell coexistence are discussed in detail in [14].
User separation in UL-OFDMA was considered in [15] for interleaved OFDMA systems. In [15], subcarriers allocated to different users follow a certain periodic structure, which leads to a user-specific CFO. Hence, by estimating the CFOs, different user signals are identified and separated. In this paper, however, we propose a semi-blind user separation algorithm that can be applied to any SAS, which does not necessarily involve any periodicity. The user separation algorithm considered in this paper is based on exploiting the differences in user CFOs and delays. In the uplink of an OFDMA system, CFOs of users vary due to the differences in oscillator frequencies as well as the Doppler shifts caused by the different velocities of users. User delays, on the other hand, vary due to the different distances of users to the UL receiver.
In this paper, we assume time synchronization to the first arriving UL user signal as well as availability of information on the basic OFDMA system parameters such as FFT size, sampling time, and cyclic prefix (CP) duration. Considering scenarios where information about block dimensions is not available, a block size estimation algorithm is devised, which exploits the correlation between the pilot subcarriers within the same block. A Gaussian approximation-based approach is then introduced, which tries to determine the potential performance of the block size estimation algorithm theoretically.
The second algorithm proposed aims at user separation. It estimates the CFOs and delays for each block separately by performing cross-correlations over pilot subcarriers and groups the blocks in the UL symbol according to their CFOs and delays using the subtractive clustering and iterative partitioning techniques. This way, it is able to determine the number of UL users and to separate their subcarriers. Flowcharts for both the block size estimation and user separation techniques are illustrated in Figures 1(a) and 1(b), respectively, which will be discussed in more detail in the later sections.
The organization of the paper is as follows. Section 2 provides the UL-OFDMA system model. In Section 3, the block size estimation method is presented, and a Gaussian approximation approach to block size estimation is given. In Section 4, a mathematical model of the proposed user separation algorithm is provided. In Section 5, the potential contribution of block size estimation and user separation algorithms to spectrum opportunity detection of cognitive radios is explained. Simulation results are presented in Section 6, and Section 7 concludes the paper.
2. UL-OFDMA System Model
Consider an OFDMA system with  users in the uplink. The sampled time domain signal at the transmitter of user
users in the uplink. The sampled time domain signal at the transmitter of user  can be written as
can be written as

where  is the total transmitted energy per symbol for user
is the total transmitted energy per symbol for user  ,
,  is the FFT size,
is the FFT size,  is the set of subcarriers with
is the set of subcarriers with  elements assigned to user
elements assigned to user  out of
out of  used subcarriers,
used subcarriers,  is the subcarrier index,
is the subcarrier index,  is the length of the cyclic prefix, and
is the length of the cyclic prefix, and  is the data on the
is the data on the  th subcarrier of
th subcarrier of  th user.
th user.
A received symbol of user  after the FFT operation can be written as
after the FFT operation can be written as

where  is the carrier frequency offset (normalized by the subcarrier spacing
is the carrier frequency offset (normalized by the subcarrier spacing  , where
, where  is the sampling frequency),
is the sampling frequency),  is the sampling clock error,
is the sampling clock error,  is the timing offset of user
is the timing offset of user  ,
,  is the random phase noise caused by the instability of user
is the random phase noise caused by the instability of user  's oscillator,
's oscillator,  is the frequency selective channel of user
is the frequency selective channel of user  ,
,  is the intercarrier interference (ICI) of user
is the intercarrier interference (ICI) of user  , and
, and  is complex additive white Gaussian noise (AWGN). In the remainder of this paper, it will be assumed that the random phase noise as well as the sampling clock error in (2) are negligible.
is complex additive white Gaussian noise (AWGN). In the remainder of this paper, it will be assumed that the random phase noise as well as the sampling clock error in (2) are negligible.
From (2), it is seen that the CFO has two effects on the received signal. First, it results in amplitude degradation and a constant phase shift, and second, in ICI. Another effect, which becomes apparent when the phases of identical pilot subcarriers in two adjacent symbols are compared [16], is a phase shift that changes linearly over symbols. Taking this linear phase shift into account, the received signal over multiple symbols can be modeled as

where  is the symbol index.
is the symbol index.
3. Block Size Estimation
Uplink OFDMA signal is composed of independent frequency allocation blocks ( 's) such as bins or tiles (tile structure in WiMAX UL-PUSC is depicted in Figure 2). A certain user may use a number of these (not necessarily adjacent) blocks in the UL, depending on its data rate requirements and scheduling information.
's) such as bins or tiles (tile structure in WiMAX UL-PUSC is depicted in Figure 2). A certain user may use a number of these (not necessarily adjacent) blocks in the UL, depending on its data rate requirements and scheduling information.
If the coexistence of the primary network and the cognitive radio is cooperative (which might be the case, e.g., in a cognitive femtocell deployment where both the macrocell and femtocells are operated by the same service provider), then the primary network might provide information about its fundamental parameters such as  ,
,  , and
, and  to the cognitive radio. Although the CR might get informed about the dimensions of
to the cognitive radio. Although the CR might get informed about the dimensions of  , as well, it is possible that the CR has to determine the block size blindly.
, as well, it is possible that the CR has to determine the block size blindly.
It is feasible to determine the block size of an UL-OFDMA system in a blind manner utilizing any received signal  that contains an arbitrary number of symbols, given that the two following assumptions are valid.
that contains an arbitrary number of symbols, given that the two following assumptions are valid.
-
(i)
The pilot subcarriers are at the corners of the resource blocks, for example, as in the PUSC mode of WiMAX standard. Note that extensions to other pilot structures may also be possible after certain modifications.
-
(ii)
In the transmitter, the (BPSK modulated) pilot subcarriers within the same resource block are assigned the same value.
Although the second condition causes some slight increase in the peak-to-average power ratio (PAPR) of the UL signal, this increase is tolerable especially in a cooperative coexistence scenario, where the primary network is willing to facilitate cognitive communications.
The pilots in each  are correlated with each other, whereas the data subcarriers are uncorrelated. Also, there is not a considerable correlation between the pilots in different
are correlated with each other, whereas the data subcarriers are uncorrelated. Also, there is not a considerable correlation between the pilots in different  s since each
s since each  is assigned a random BPSK value for its pilots. The dimensions of
is assigned a random BPSK value for its pilots. The dimensions of  can be determined by exploiting the correlation between the pilots within the
can be determined by exploiting the correlation between the pilots within the  s.
s.
The vertical dimension of  can be found by performing autocorrelation over an entire symbol (vertical correlation), where it is assumed that the orientation of subcarriers versus symbols is as depicted in Figure 2. Without taking the effects of delays and CFOs into consideration, we define the absolute value of the vertical correlation as
can be found by performing autocorrelation over an entire symbol (vertical correlation), where it is assumed that the orientation of subcarriers versus symbols is as depicted in Figure 2. Without taking the effects of delays and CFOs into consideration, we define the absolute value of the vertical correlation as

where  is the lag index,
is the lag index,  denotes the expectation operation,
denotes the expectation operation,  is the separation between the pilots in the same symbol of
is the separation between the pilots in the same symbol of  ,
,  is the average subcarrier power, and
is the average subcarrier power, and  is the noise power. Note that the expectation is performed over all subcarriers, and the
is the noise power. Note that the expectation is performed over all subcarriers, and the  term is the ratio of the number of pilot pairs in a symbol (number of
term is the ratio of the number of pilot pairs in a symbol (number of  s) to the number of occupied subcarriers
s) to the number of occupied subcarriers  .
.
In a similar manner, the horizontal dimension of  can be obtained via an autocorrelation over rows (horizontal correlation), where a row is the set of subcarriers at the same subcarrier index
can be obtained via an autocorrelation over rows (horizontal correlation), where a row is the set of subcarriers at the same subcarrier index  . The absolute value of the horizontal correlation is given by
. The absolute value of the horizontal correlation is given by

where  is the separation between the pilots in the same row of
is the separation between the pilots in the same row of  . The expectation is performed over all symbols involved in the correlation, and the
. The expectation is performed over all symbols involved in the correlation, and the  term is the ratio of the number of pilot pairs (number of
term is the ratio of the number of pilot pairs (number of  s) to the number of nonempty subcarriers in a row.
s) to the number of nonempty subcarriers in a row.
In both vertical and horizontal correlations, the desired peak is the one that is strongest after the peak at the origin. In order to accentuate the desired peak, noise averaging is performed by averaging  over all symbols available and by averaging
over all symbols available and by averaging  over
over  rows. The desired peak in the vertical correlation is expected to appear at the
rows. The desired peak in the vertical correlation is expected to appear at the  th lag yielding the vertical dimension of
th lag yielding the vertical dimension of  as
as  +1. Similarly, the horizontal dimension is obtained from the horizontal correlation as
+1. Similarly, the horizontal dimension is obtained from the horizontal correlation as  +1.
+1.
An illustrative example of the vertical and horizontal correlations is provided in Figure 3, where the main peaks are normalized to 1. The block dimensions that need to be determined are 4 subcarriers by 3 symbols ( ) as in Figure 2. Hence, peaks are observed in the 3rd lag in the vertical correlation and in the 2nd lag in the horizontal correlation. In Figures 3(a) and 3(b), the theoretical curves represent the values provided by (4) and (5), where the delays and CFOs are not taken into account. Under the effect of delays and CFOs, the second curves are obtained, where the desired peaks appear weaker than the theoretical values. The reason for the weakening of the desired peaks is that the delays and CFOs introduce different correlations to the subcarriers of each user, which, in effect, deteriorates the overall correlations of the pilots. Finally, the correlation values that are obtained in a practical simulation are plotted, where the desired peaks are considerably weaker. This is because in a practical scenario, the vertical correlations are averaged over all symbols, only
) as in Figure 2. Hence, peaks are observed in the 3rd lag in the vertical correlation and in the 2nd lag in the horizontal correlation. In Figures 3(a) and 3(b), the theoretical curves represent the values provided by (4) and (5), where the delays and CFOs are not taken into account. Under the effect of delays and CFOs, the second curves are obtained, where the desired peaks appear weaker than the theoretical values. The reason for the weakening of the desired peaks is that the delays and CFOs introduce different correlations to the subcarriers of each user, which, in effect, deteriorates the overall correlations of the pilots. Finally, the correlation values that are obtained in a practical simulation are plotted, where the desired peaks are considerably weaker. This is because in a practical scenario, the vertical correlations are averaged over all symbols, only  of which contain pilot subcarriers; and the horizontal correlations are averaged over all rows,
of which contain pilot subcarriers; and the horizontal correlations are averaged over all rows,  of which contain pilots. Therefore, the heights of the desired peaks for the practical case are
of which contain pilots. Therefore, the heights of the desired peaks for the practical case are  and
and  for the vertical and horizontal correlations, respectively, which are equal to each other.
for the vertical and horizontal correlations, respectively, which are equal to each other.
3.1. Gaussian Approximation for Block Size Estimation
In both vertical and horizontal correlations performed for block size estimation, each of the samples in the output of the correlation can be approximated using Gaussian approximation (GA). Ignoring the sample at the zeroth lag, all of the correlation samples have a zero mean except the sample at the desired peak location. Therefore, the problem of detecting a peak at the correlator output can actually be considered as finding a variable with a nonzero mean within a group of zero-mean variables.
Let  and
and  denote the mean and the standard deviation of a correlation value
denote the mean and the standard deviation of a correlation value  at the
at the  th lag, respectively. If
th lag, respectively. If  denotes the lag corresponding to the peak of the correlation outputs, then we have
denotes the lag corresponding to the peak of the correlation outputs, then we have  , and
, and  is equal to zero otherwise. Taking into account that the peak detection is performed after absolute value operation, the probability density function of
is equal to zero otherwise. Taking into account that the peak detection is performed after absolute value operation, the probability density function of  can be written as
can be written as

In order for  to have the largest amplitude, all other samples at the other correlation lags need to have absolute values that are smaller than
to have the largest amplitude, all other samples at the other correlation lags need to have absolute values that are smaller than  . This has a probability of
. This has a probability of  , where
, where  is the half-length of the correlator output excluding the sample at the zeroth lag. Therefore, the total probability of detection of peak of the correlation output can be obtained by the following equation:
is the half-length of the correlator output excluding the sample at the zeroth lag. Therefore, the total probability of detection of peak of the correlation output can be obtained by the following equation:

Performing (7) for both horizontal and vertical correlations yields the probabilities of detecting the corresponding peaks. Denoting these two probabilities as  and
and  , the probability of detecting the block size correctly is simply equal to
, the probability of detecting the block size correctly is simply equal to  .
.
Note that (7) is an approximation due to two primary reasons. First, as discussed before, noise-cross-noise terms in the pilot correlations are approximated using a GA. Secondly, all of the correlation samples are assumed to be uncorrelated random variables, which is not true in practice. The existence of delays introduces correlation between subcarriers in the same symbol, and the CFOs result in correlation between subcarriers in adjacent symbols. Despite these factors, it will be shown in Section 6 that the approximation yields relatively close results to the simulation results, especially when the block size is estimated over large number of symbols.
4. User Separation Method
The proposed user separation method is based on exploiting the differences in the  's and
's and  's of different UL-OFDMA users. The first step of the method is to determine the occupied
's of different UL-OFDMA users. The first step of the method is to determine the occupied  's via energy detection. Then, for each occupied
's via energy detection. Then, for each occupied  , the UL receiver performs
, the UL receiver performs  and
and  estimation. Next, occupied
estimation. Next, occupied  's are clustered according to their
's are clustered according to their  and
and  values, where each separate cluster yields the
values, where each separate cluster yields the  's that belong to a certain user. This way,
's that belong to a certain user. This way,  , which is an estimate for
, which is an estimate for  , is obtained for each user
, is obtained for each user  .
.
The total energy of each block  can be calculated as follows:
can be calculated as follows:

This energy value is averaged over the subcarriers within the block and inputted to an energy detector that employs a threshold  as follows:
as follows:

where hypothesis  implies that block
implies that block  is occupied, and hypothesis
is occupied, and hypothesis  implies that it is not. Details of energy detection in OFDMA-UL, such as optimizing
implies that it is not. Details of energy detection in OFDMA-UL, such as optimizing  , can be found in [17]. Let
, can be found in [17]. Let  denote the set of all the occupied
denote the set of all the occupied  's that satisfy the hypothesis
's that satisfy the hypothesis  in (9). Then, for each
in (9). Then, for each  within
within  , carrier frequency offset and delay estimations are performed.
, carrier frequency offset and delay estimations are performed.
Regarding the CFO estimation, an important observation from (3) is that the linear phase shift caused by the CFO affects both the desired signal and ICI the same way. Therefore, a reliable  estimate can be obtained by correlating two identical pilot symbols [16] or pilot subcarriers in different symbols as illustrated in Figure 2. If
estimate can be obtained by correlating two identical pilot symbols [16] or pilot subcarriers in different symbols as illustrated in Figure 2. If  denotes the indices of symbols (within the
denotes the indices of symbols (within the  th block) that carry pilot subcarriers and
th block) that carry pilot subcarriers and  denotes the subcarrier indices of pilots in symbol
denotes the subcarrier indices of pilots in symbol  within
within  , a
, a  estimate for
estimate for  , which will be denoted as
, which will be denoted as  , can be obtained by performing pairwise correlation between
, can be obtained by performing pairwise correlation between  in different symbols within
in different symbols within  , separated by
, separated by  symbols. Ignoring the ICI and noise terms, this correlation would be as follows:
symbols. Ignoring the ICI and noise terms, this correlation would be as follows:

where symbol  is within
is within  .
.  can then be obtained as
can then be obtained as

where

The timing offset causes a phase shift that changes linearly over the subcarriers but is independent from the symbol index. If  denotes indices of rows with pilots within
denotes indices of rows with pilots within  , a
, a  estimate for
estimate for  , which will be denoted as
, which will be denoted as  , can be obtained by correlating pilots at different rows separated by
, can be obtained by correlating pilots at different rows separated by  subcarriers (illustrated in Figure 2) as
subcarriers (illustrated in Figure 2) as

where subcarrier  is within
is within  . The
. The  estimate for
estimate for  is obtained as follows:
is obtained as follows:

where

As seen from (10), an important condition necessary for  to be reliable is that the channel can be considered constant during
to be reliable is that the channel can be considered constant during  symbols. Taking the WiMAX standard as a reference, Table 2 [18] provides information about channel coherence times for two different frequency bands. Given that the WiMAX symbol duration is around 0.1 ms, the channel coherence time covers up to 20 symbols even at a speed of 100 km/h in the 5.8 GHz band. Similarly, for any typical OFDMA-based standard, it can be expected that this channel constancy condition is met.
symbols. Taking the WiMAX standard as a reference, Table 2 [18] provides information about channel coherence times for two different frequency bands. Given that the WiMAX symbol duration is around 0.1 ms, the channel coherence time covers up to 20 symbols even at a speed of 100 km/h in the 5.8 GHz band. Similarly, for any typical OFDMA-based standard, it can be expected that this channel constancy condition is met.
Equation (13) also introduces a similar requirement in the frequency dimension. A reliable  can only be obtained if
can only be obtained if  for pilots separated by
for pilots separated by  subcarriers are highly correlated. Although this condition is met for any
subcarriers are highly correlated. Although this condition is met for any  in a single tap channel, in a frequency selective channel,
in a single tap channel, in a frequency selective channel,  is typically taken as a small number (e.g., in the WiMAX UL-PUSC system
is typically taken as a small number (e.g., in the WiMAX UL-PUSC system  is defined as 3).
is defined as 3).
Once  's and
's and  's are obtained for all elements of
's are obtained for all elements of  , the user separation algorithm requires that
, the user separation algorithm requires that  's be clustered according to their
's be clustered according to their  's and
's and  's, taking both values into account simultaneously. Each separate cluster generated by the clustering algorithm corresponds to a different user
's, taking both values into account simultaneously. Each separate cluster generated by the clustering algorithm corresponds to a different user  and yields its subcarrier allocation vector estimate
and yields its subcarrier allocation vector estimate  .
.
The clustering method first yields an estimate for the number of users ( ), which is determined by finding the cluster centers through the subtractive clustering algorithm outlined in [19, 20]. A critical input required by the subtractive clustering algorithm is the ratio of dimensions of the potential clusters, which will be denoted as
), which is determined by finding the cluster centers through the subtractive clustering algorithm outlined in [19, 20]. A critical input required by the subtractive clustering algorithm is the ratio of dimensions of the potential clusters, which will be denoted as  and
and  . In the next step, utilizing
. In the next step, utilizing  , the separation is performed via iterative partitioning algorithm discussed in [21, 22]. Iterative partitioning splits the input data into
, the separation is performed via iterative partitioning algorithm discussed in [21, 22]. Iterative partitioning splits the input data into  initial clusters. Then, for each cluster, it computes the sum of absolute distances from each point in the cluster to the cluster centroid, where the centroid is the component wise median of the points in the cluster. By minimizing the total of these sums in an iterative manner, the clusters are determined.
initial clusters. Then, for each cluster, it computes the sum of absolute distances from each point in the cluster to the cluster centroid, where the centroid is the component wise median of the points in the cluster. By minimizing the total of these sums in an iterative manner, the clusters are determined.
Prior to applying the clustering method, the sets of  's and
's and  's, which will be denoted as
's, which will be denoted as  and
and  , respectively, need to be normalized. The normalization is mandated by the fact that the range of numerical values for
, respectively, need to be normalized. The normalization is mandated by the fact that the range of numerical values for  is wider than the range of
is wider than the range of  's by at least two orders of magnitude. In fact, clustering without normalization results in a user separation that is solely based on
's by at least two orders of magnitude. In fact, clustering without normalization results in a user separation that is solely based on  values. In particular, we apply the following normalizations:
values. In particular, we apply the following normalizations:


respectively, which map both  and
and  into the interval
into the interval  . Therefore, as shown in Figure 4, the clustering is performed on a
. Therefore, as shown in Figure 4, the clustering is performed on a  plane.
plane.
A second point related to the subtractive clustering algorithm is that it requires to optimize the ratio of cluster dimensions for the best performance. This ratio ( ) is proportional to the ratio of variances of
) is proportional to the ratio of variances of  and
and  , that is,
, that is,  , which are related to each other as follows:
, which are related to each other as follows:

where  and
and  denote the sets of all
denote the sets of all  's and
's and  's, respectively. The
's, respectively. The  input of the subtractive clustering algorithm is set as
input of the subtractive clustering algorithm is set as  . From (18), it is seen that the wider the range of values that
. From (18), it is seen that the wider the range of values that  can take, the smaller is the
can take, the smaller is the  dimension of the clusters (the same analogy applies
dimension of the clusters (the same analogy applies  dimension, as well). Moreover, (18) also indicates that
dimension, as well). Moreover, (18) also indicates that  can be found before performing clustering by simply calculating the ratio of
can be found before performing clustering by simply calculating the ratio of  to
to  . An important assumption regarding (18) is that the
. An important assumption regarding (18) is that the  and
and  values of different users are uniformly spread within
values of different users are uniformly spread within  and
and  , respectively.
, respectively.
A visual example that illustrates the clustering algorithm is provided in Figure 4. It shows the clusters in a 10-user scenario, where SNR is assumed to be  dB for all user signals, and a multipath (MP) channel is considered along with the delay and CFO values in Table 1. In Figure 4, the large red dots constitute the cluster centers found through subtractive clustering, and the markers surrounding each of them indicate the resource blocks that belong to a certain user determined through iterative partitioning.
dB for all user signals, and a multipath (MP) channel is considered along with the delay and CFO values in Table 1. In Figure 4, the large red dots constitute the cluster centers found through subtractive clustering, and the markers surrounding each of them indicate the resource blocks that belong to a certain user determined through iterative partitioning.
5. Using Block Size Estimation and User Separation in Spectrum Opportunity Detection
Opportunistic spectrum usage is one of the main goals of a cognitive radio. It requires that the CR reliably determine the temporarily empty parts of the spectrum of a primary network and utilize them without causing any interference to the primary network. In this section, we propose techniques that make use of the user separation and block size estimation methods proposed in the previous sections in order to improve the opportunity detection performance.
In an OFDMA-based primary network, the spectrum opportunities correspond to the unused subcarriers within the spectrum. A simple method that might be employed for the detection of these opportunities by the cognitive radios is energy detection, where, the unused subcarriers may be simply identified through hytpothesis test as follows:

Note that similar to (9), hypothesis  implies that a subcarrier is occupied, and hypothesis
implies that a subcarrier is occupied, and hypothesis  implies that it is not. However, with subcarrier-based opportunity detection as in (19), each of the individual subcarriers is subject to false alarms and misdetections. As an alternative, if the resource block size is perfectly known, the opportunities within the spectrum of a primary system can be determined via tile-based energy detection using (9). Since all the subcarriers within the same tile should all be affiliated with the same hypothesis (i.e., all subcarriers should be occupied, or all subcarriers should be nonoccupied), probability of misdetections and probability of false-alarms will be minimized compared to the subcarrier-based detection. If the resource block size is not known, on the other hand, block size detection algorithm as in Section 3 can be utilized to estimate the resource block dimensions and improve the opportunity detection performance with respect to the subcarrier-based detection.
implies that it is not. However, with subcarrier-based opportunity detection as in (19), each of the individual subcarriers is subject to false alarms and misdetections. As an alternative, if the resource block size is perfectly known, the opportunities within the spectrum of a primary system can be determined via tile-based energy detection using (9). Since all the subcarriers within the same tile should all be affiliated with the same hypothesis (i.e., all subcarriers should be occupied, or all subcarriers should be nonoccupied), probability of misdetections and probability of false-alarms will be minimized compared to the subcarrier-based detection. If the resource block size is not known, on the other hand, block size detection algorithm as in Section 3 can be utilized to estimate the resource block dimensions and improve the opportunity detection performance with respect to the subcarrier-based detection.
As a third technique, we also propose an additional method in order to decrease the false-alarm probability of the block- (tile) based opportunity detection with perfect block size knowledge. In this approach, which we will call user separation-based opportunity detection, we consider each resource block with index  that is estimated to belong to hypothesis
that is estimated to belong to hypothesis  (i.e., detected as occupied). Then, hypothesis for the resource block
(i.e., detected as occupied). Then, hypothesis for the resource block  is changed to
is changed to  if any of the following criteria is satisfied for the resource block:
if any of the following criteria is satisfied for the resource block:
-
(i)
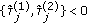 , that is, the delay estimates for tile-
, that is, the delay estimates for tile-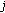 are smaller than
are smaller than  .
. -
(ii)
 , that is, different delay estimates for the same resource block have a considerably large difference.
, that is, different delay estimates for the same resource block have a considerably large difference. -
(iii)
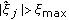 , that is, the absolute value of the CFO estimate for tile-
, that is, the absolute value of the CFO estimate for tile-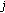 is larger than the maximum possible CFO value.
is larger than the maximum possible CFO value. -
(iv)
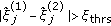 , that is, different CFO estimates for the same resource block have a considerably large difference.
, that is, different CFO estimates for the same resource block have a considerably large difference.
As will be shown in Section 6, the performance of user separation-based opportunity detection can be improved using the above tests that pose some constraints on the occupied resource blocks.
6. Simulation Results
Computer simulations were performed in order to determine the success rate in blind block size estimation, to test the performance of the proposed user separation algorithm, and to determine the opportunity detection performance using various methods. In the simulations, the basic system parameters are set according to the WiMAX UL-PUSC standard, and both an AWGN channel and a 6-tap multipath channel (ITU-R Vehicular A) are employed. Detailed simulation parameters are provided in Table 1, where RTD stands for the round-trip-delay.
6.1. Block Size Estimation Simulations
The performances of the block size estimation method as well as the Gaussian approximation are simulated using two separate  's that are 60 symbols and 120 symbols long. The variation of the performances with respect to signal-to-noise ratio (SNR) is plotted for both AWGN and multipath (MP) channels in Figures 5 and 6, where the block sizes to be found are
's that are 60 symbols and 120 symbols long. The variation of the performances with respect to signal-to-noise ratio (SNR) is plotted for both AWGN and multipath (MP) channels in Figures 5 and 6, where the block sizes to be found are  and
and  , respectively. The results show that the performance heavily depends on the block size. While the simulated performance is 100% in all cases examined for the
, respectively. The results show that the performance heavily depends on the block size. While the simulated performance is 100% in all cases examined for the  block, it can be around 70% for the
block, it can be around 70% for the  block when the SNR is low. There are two reasons for the relatively lower performance for the
block when the SNR is low. There are two reasons for the relatively lower performance for the  block. First, the number of symbols and rows with pilot subcarriers is lower, which weakens the desired correlation peaks. And second, the physical separation between the pilots is larger, which, in a MP channel, decreases the correlation between them due to the variation of the channel in time and frequency. It is also worth to note that the Gaussian approximation matches with the simulation results quite well for the
block. First, the number of symbols and rows with pilot subcarriers is lower, which weakens the desired correlation peaks. And second, the physical separation between the pilots is larger, which, in a MP channel, decreases the correlation between them due to the variation of the channel in time and frequency. It is also worth to note that the Gaussian approximation matches with the simulation results quite well for the  block. The match between the simulations and the GA is still acceptable for the
block. The match between the simulations and the GA is still acceptable for the  block when 120 symbols are available. When there are just 60 symbols, however, there is an apparent difference between them. This is due to the fact that
block when 120 symbols are available. When there are just 60 symbols, however, there is an apparent difference between them. This is due to the fact that  cannot be estimated reliably over 60 symbols, and also the correlation between the nonpilot subcarriers has a nonzero value that is considerably larger than in case of 120 symbols.
cannot be estimated reliably over 60 symbols, and also the correlation between the nonpilot subcarriers has a nonzero value that is considerably larger than in case of 120 symbols.
6.2. User Separation Simulations
Performance of the proposed user separation algorithm was tested via simulations using the following performance metrics.
Performance in finding the number of users is given as

Performance in finding the user subcarriers is given as

where  is the Dirac delta function. The performances obtained in AWGN and MP channels using a
is the Dirac delta function. The performances obtained in AWGN and MP channels using a  block are demonstrated in Figure 7. The assumption in the corresponding simulations was that the received SNR is the same for all users regardless of their distance. Note that if the cognitive radio performing user separation is close to the primary receiver, such a scenario may be valid. Due to power control, the SNRs of the received UL signals at the primary receiver (e.g., a macrocell BS) would be similar; hence, a close-by cognitive radio (e.g., a femtocell BS) would also observe similar SNR levels. The performance at each SNR is maximized by employing the optimum cluster dimension given by
block are demonstrated in Figure 7. The assumption in the corresponding simulations was that the received SNR is the same for all users regardless of their distance. Note that if the cognitive radio performing user separation is close to the primary receiver, such a scenario may be valid. Due to power control, the SNRs of the received UL signals at the primary receiver (e.g., a macrocell BS) would be similar; hence, a close-by cognitive radio (e.g., a femtocell BS) would also observe similar SNR levels. The performance at each SNR is maximized by employing the optimum cluster dimension given by  . The results show that better than 90% user separation performance is achievable for sufficiently high SNR values.
. The results show that better than 90% user separation performance is achievable for sufficiently high SNR values.
In Table 3, additional simulation results are provided for a practical scenario, where the received powers from different users depend on their distances to the receiver as specified in Table 1 (free space path loss model is considered). The transmission power of users is 27 dBm, and the received signal SNRs descend from 30 dB towards 5 dB. The blocks whose power levels do not exceed a certain threshold are discarded as in (9). Simulation results in Table 3 show that  values that exceed 80% and
values that exceed 80% and  values close to 80% are achievable.
values close to 80% are achievable.
Another analysis is performed to investigate the effect of number of users on the performance in finding the user subcarriers.  is obtained for
is obtained for  values 5, 10, and 20. The CFOs of users are equally spaced between
values 5, 10, and 20. The CFOs of users are equally spaced between  Hz and 500 Hz, while the user distances are equally spaced between
Hz and 500 Hz, while the user distances are equally spaced between  and 2000 meters. The
and 2000 meters. The  curves obtained for both AWGN and MP channels are shown in Figure 8. It is observed that a smaller user number such as 5 yields considerably higher performance, especially in AWGN channel. It is also important to note that when the SNR level is high enough, even 20 user signals can be separated with an accuracy rate that exceeds 80%.
curves obtained for both AWGN and MP channels are shown in Figure 8. It is observed that a smaller user number such as 5 yields considerably higher performance, especially in AWGN channel. It is also important to note that when the SNR level is high enough, even 20 user signals can be separated with an accuracy rate that exceeds 80%.
6.3. Opportunity Detection Simulations
The results of the opportunity detection simulations are demonstrated in Figures 9 and 10. The error probability is computed as the sum of probability of false alarms (PFAs) and probability of missed detections (PMDs). PFA is the ratio of the number of subcarriers detected as used although they are unused to  , whereas PMD is defined as the ratio of number of subcarriers detected as unused although they are used to
, whereas PMD is defined as the ratio of number of subcarriers detected as unused although they are used to  . In the related simulations, the occupancy rate of the subcarriers is kept at 50% to have equal contribution from PMD and PFA to the total error probability.
. In the related simulations, the occupancy rate of the subcarriers is kept at 50% to have equal contribution from PMD and PFA to the total error probability.
In Figure 9, the error probabilities for four different methods are shown for an optimum ( ) and for a nonoptimum (
) and for a nonoptimum ( ) normalized threshold value, where the block size of the primary system is
) normalized threshold value, where the block size of the primary system is  . The methods that are employed are subcarrier based, user separation based, tile based with known tile size, and tile based with estimated tile size. It is observed that the subcarrier-based method yields the worst performance, while the tile-based method performs the best. Therefore, if the tile size is not known, instead of employing the subcarrier-based method, first the proposed tile size estimation can be performed and then the tile-based detection method can be applied. Given that the proposed tile size estimation for this small block size is very accurate, this way, the detection performance can be made as good as in the known tile size case. User separation-based method is seen to introduce some errors and to degrade the performance when the threshold is optimum. If the optimum threshold is not available and an intuitive value such as 0.5 is employed, however, then the user separation-based method improves the performance.
. The methods that are employed are subcarrier based, user separation based, tile based with known tile size, and tile based with estimated tile size. It is observed that the subcarrier-based method yields the worst performance, while the tile-based method performs the best. Therefore, if the tile size is not known, instead of employing the subcarrier-based method, first the proposed tile size estimation can be performed and then the tile-based detection method can be applied. Given that the proposed tile size estimation for this small block size is very accurate, this way, the detection performance can be made as good as in the known tile size case. User separation-based method is seen to introduce some errors and to degrade the performance when the threshold is optimum. If the optimum threshold is not available and an intuitive value such as 0.5 is employed, however, then the user separation-based method improves the performance.
Error probability curves obtained for a block size of  are demonstrated in Figure 10. Being different from the
are demonstrated in Figure 10. Being different from the  case, for a
case, for a  block, the block size estimation method does not perform very well. Therefore, the subcarrier-based detection method is superior to the tile-based method with tile size estimation. It is noteworthy that the user separation-based method is slightly superior to the tile-based method for both optimum and nonoptimum thresholds.
block, the block size estimation method does not perform very well. Therefore, the subcarrier-based detection method is superior to the tile-based method with tile size estimation. It is noteworthy that the user separation-based method is slightly superior to the tile-based method for both optimum and nonoptimum thresholds.
7. Concluding Remarks
In order to increase the spectrum awareness of OFDMA-based cognitive radios, separation of primary user signals in the uplink is proposed. An algorithm is devised for determining the frequency allocation block dimensions blindly. The probability of finding the block size correctly is obtained through a Gaussian approximation-based approach, and it is compared with the simulated performance of the devised algorithm. Moreover, a user separation method is proposed, and a rather high performance is obtained in practical computer simulations proving its feasibility. Spectrum opportunity detection is highlighted as a potential application area where the proposed methods might be considerably useful. The improvement in opportunity detection performance of cognitive radios is quantified through simulations and shown to be significant.
References
Mangold S, Zhong Z, Hiertz GR, Walke B: IEEE 802.11e/802.11k wireless LAN: spectrum awareness for distributed resource sharing. Wireless Communications and Mobile Computing 2004, 4(8):881-902. 10.1002/wcm.261
Sai Shankar N, Cordeiro C, Challapali K: Spectrum agile radios: utilization and sensing architectures. Proceedings of the 1st IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '05), November 2005 160-169.
Haykin S: Cognitive radio: brain-empowered wireless communications. IEEE Journal on Selected Areas in Communications 2005, 23(2):201-220.
Akyildiz IF, Lee W-Y, Vuran MC, Mohanty S: NeXt generation/dynamic spectrum access/cognitive radio wireless networks: a survey. Computer Networks 2006, 50(13):2127-2159. 10.1016/j.comnet.2006.05.001
Yucek T, Arslan H: Spectrum characterization for opportunistic cognitive radio systems. Proceedings of IEEE Military Communications Conference (MILCOM '06), October 2006, Washington, DC, USA 1-6.
Pun M-O, Morelli M, Kuo C-CJ: Maximum-likelihood synchronization and channel estimation for OFDMA uplink transmissions. IEEE Transactions on Communications 2006, 54(4):726-736.
Cao Z, Tureli U, Yao Y-D: Deterministic multiuser carrier-frequency offset estimation for interleaved OFDMA uplink. IEEE Transactions on Communications 2004, 52(9):1585-1594. 10.1109/TCOMM.2004.833183
van de Beek J-J, Sandell M, Börjesson PO: ML estimation of time and frequency offset in OFDM systems. IEEE Transactions on Signal Processing 1997, 45(7):1800-1805. 10.1109/78.599949
Morelli M: Timing and frequency synchronization for the uplink of an OFDMA system. IEEE Transactions on Communications 2004, 52(2):296-306. 10.1109/TCOMM.2003.822699
Fantacci R, Marabissi D, Papini S: Multiuser interference cancellation receivers for OFDMA uplink communications with carrier frequency offset. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '04), November 2004, Dallas, Tex, USA 5: 2808-2812.
Kim K, Han Y, Kim S-L: Joint subcarrier and power allocation in uplink OFDMA systems. IEEE Communications Letters 2005, 9(6):526-528. 10.1109/LCOMM.2005.1437359
Chandrasekhar V, Andrews JG, Gatherer A: Femtocell networks: a survey. IEEE Communications Magazine 2008, 46(9):59-67.
Claussen H: Performance of macro- and co-channel femtocells in a hierarchical cell structure. Proceedings of the 18th Annual IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC '07), September 2007, Athens, Greece 1-5.
Şahin ME, Guvenc I, Jeong M-R, Arslan H: User separation for OFDMA uplink. Proceedings of IEEE Vehicular Technology Conference (VTC '09), April 2009, Barcelona, Spain
Cao Z, Tureli U, Yao Y-D: User separation and frequency-time synchronization for the uplink of interleaved OFDMA. Proceedings of Conference Record of the Asilomar Conference on Signals, Systems and Computers, November 2002, Pacific Grove, Calif, USA 2: 1842-1846.
Moose PH: A technique for orthogonal frequency division multiplexing frequency offset correction. IEEE Transactions on Communications 1994, 42(10):2908-2914. 10.1109/26.328961
Şahin ME, Guvenc I, Jeong M-R, Arslan H: Opportunity detection for OFDMA systems with timing misalignment. Proceedings of IEEE Global Telecommunications Conference (GLOBECOM '08), November-December 2008, New Orleans, La, USA 3913-3918.
Andrews JG, Ghosh A, Muhamed R: Fundamentals of WiMAX: Understanding Broadband Wireless Networking. Prentice-Hall, Englewood Cliffs, NJ, USA; 2007.
Chiu S: Fuzzy model identification based on cluster estimation. Journal of Intelligent and Fuzzy Systems 1994, 2(3):267-278.
Yager R, Filev D: Generation of fuzzy rules by mountain clustering. Journal of Intelligent and Fuzzy Systems 1994, 2(3):209-219.
Seber G: Multivariate Observations. John Wiley & Sons, New York, NY, USA; 1984.
Spath H: Cluster Dissection and Analysis: Theory, FORTRAN Programs, Examples. Horwood, New York, NY, USA; Halsted Press, Chichester, UK; 1985.
Acknowledgments
The authors would like to thank Dr. Moo-Ryong Jeong and Dr. Fujio Watanabe of DOCOMO Communications Labs, USA, for their helpful inputs. This paper was presented in part at the IEEE Vehicular Technology Conference (VTC-2009 Spring), Barcelona, Spain, April 2009.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Şahin, M., Guvenc, I. & Arslan, H. Uplink User Signal Separation for OFDMA-Based Cognitive Radios. EURASIP J. Adv. Signal Process. 2010, 502369 (2009). https://doi.org/10.1155/2010/502369
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/502369


 are illustrated in the first block, while the correlations for obtaining
are illustrated in the first block, while the correlations for obtaining  are illustrated in the second block.
are illustrated in the second block.

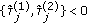 , that is, the delay estimates for tile-
, that is, the delay estimates for tile-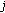 are smaller than
are smaller than  .
. , that is, different delay estimates for the same resource block have a considerably large difference.
, that is, different delay estimates for the same resource block have a considerably large difference.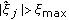 , that is, the absolute value of the CFO estimate for tile-
, that is, the absolute value of the CFO estimate for tile-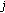 is larger than the maximum possible CFO value.
is larger than the maximum possible CFO value.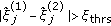 , that is, different CFO estimates for the same resource block have a considerably large difference.
, that is, different CFO estimates for the same resource block have a considerably large difference.




