- Research Article
- Open access
- Published:
Automatic Determination of Fiber-Length Distribution in Composite Material Using 3D CT Data
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 545030 (2010)
Abstract
Determining fiber length distribution in fiber reinforced polymer components is a crucial step in quality assurance, since fiber length has a strong influence on overall strength, stiffness, and stability of the material. The approximate fiber length distribution is usually determined early in the development process, as conventional methods require a destruction of the sample component. In this paper, a novel, automatic, and nondestructive approach for the determination of fiber length distribution in fiber reinforced polymers is presented. For this purpose, high-resolution computed tomography is used as imaging method together with subsequent image analysis for evaluation. The image analysis consists of an iterative process where single fibers are detected automatically in each iteration step after having applied image enhancement algorithms. Subsequently, a model-based approach is used together with a priori information in order to guide a fiber tracing and segmentation process. Thereby, the length of the segmented fibers can be calculated and a length distribution can be deduced. The performance and the robustness of the segmentation method is demonstrated by applying it to artificially generated test data and selected real components.
1. Introduction
Fiber reinforced polymers (FRPs) are used increasingly in the aerospace and automotive industry, since those components facilitate the cost-effective building of lightweight but rigid components. One manufacturing method for the construction of fiber reinforced polymers is the long fiber reinforced thermoplastics (LFRP-D) process, where a matrix material, for example consisting of polypropylene and additives, is heated and mixed with fibers, for example carbon or glass fibers. This process happens directly, that is, without the usage of an intermediate semifinished part. Thereby, components can be manufactured that are capable of acting as supporting elements with respect to rigidity and stability. Due to these properties, many parts made of LFRP are already used in the automotive industry, for example for frontends, underbody casing, supporting elements, or parts of an engine compartment.
The length of the fibers has a strong influence on the strength, stiffness, and impact resistance of the component [1]. From measurements, it is known that 95% of the maximal possible material stiffness is reached at a fiber length of 1 mm. However, the desirable length of fibers within a certain component is strongly dependent on the purpose of the product [2]. Moreover, since fibers can be damaged and divided by the production device during the creation process, there is not only one single fiber length but a distribution of the fiber lengths within a component. Furthermore, the opposite can happen if the cutting of the fibers by the cutting unit does not work well, which results in longer fibers than expected [3]. Because of this uncertainty of the actual fiber length within the component, it is important to determine the distribution of the fibers and their lengths after the production process in order to estimate the quality of the resulting product.
In this paper, a novel method for the determination of the fiber length distribution is proposed using high resolution computed tomography as scanning method. Therefore, the 3D CT image is processed in order to segment the fibers. Subsequently, the length of each segmented fiber can be calculated and their distribution can be quantified. As a consequence, the presented method avoids destruction of the test sample and makes an inspection of in-use products feasible.
The remaining sections of this paper are structured as follows. Section 2 briefly discusses the current methods in fiber length distribution determination. Following in Section 3, our algorithm for automatic fiber segmentation and length calculation on high-resolution CT images of components is explained. The results achieved by applying this method to artificial and real datasets are presented in Section 4. The concluding Section 5 contains a discussion of the presented method and gives an outlook to planned future research topics in this area.
2. Previous Work
The established method for the determination of a fiber length distribution within a component is to pyrolyze its matrix [4, 5]. Therefore, the component is put into an oven which is heated to about  . After about 90 minutes, the matrix component is reduced to ashes and the skeleton of the fibers remain. In order to determine their length distribution, several methods are possible and in use. One mechanical process is to sieve the fibers with different sieve sizes. However, this method does not work satisfactory with long fibers that are strongly felted. Another common method is the usage of scanners or high-resolution CCD-cameras and flash devices [5]. For this method, the fibers have to be singularized in order to reduce measurement errors caused by fiber crossings and fiber entanglements. Subsequently, the fibers are segmented with a digital image analysis system and the length of the segmented fibers is determined.
. After about 90 minutes, the matrix component is reduced to ashes and the skeleton of the fibers remain. In order to determine their length distribution, several methods are possible and in use. One mechanical process is to sieve the fibers with different sieve sizes. However, this method does not work satisfactory with long fibers that are strongly felted. Another common method is the usage of scanners or high-resolution CCD-cameras and flash devices [5]. For this method, the fibers have to be singularized in order to reduce measurement errors caused by fiber crossings and fiber entanglements. Subsequently, the fibers are segmented with a digital image analysis system and the length of the segmented fibers is determined.
The main disadvantage of these approaches is that the component has to be destroyed in order to determine fiber lengths. Consequently, these methods can only be applied during the development process for the first article inspection or the evaluation of spot samples. Therefore, it would be strongly desirable to have methods that allow for the non-destructive evaluation of in-use products or parts thereof for quality assessment. However, currently there are only limited non-destructive evaluation technologies available or under active research [6].
The use of Micro-CT ( CT) technology allows for three dimensional imaging of structures with a very high spatial resolution (up to 700 nanometers). Therefore, it is possible to acquire high-quality images of the inside of components built with fiber reinforced polymers, since these fibers exhibit diameters of well below
CT) technology allows for three dimensional imaging of structures with a very high spatial resolution (up to 700 nanometers). Therefore, it is possible to acquire high-quality images of the inside of components built with fiber reinforced polymers, since these fibers exhibit diameters of well below  mm. A corresponding 3D view of a
mm. A corresponding 3D view of a  CT scan of a LFRP sample is shown in Figure 1.
CT scan of a LFRP sample is shown in Figure 1.
Due to high resolution scanning technology combined with a high image quality, the development of non-destructive evaluation algorithms becomes more and more practical. In the following section, a model-based approach for the automatic detection and segmentation of fibers from such image data is presented.
3. Fiber Segmentation
A model of an ideal fiber is the foundation of the following segmentation approach. It is reasonable to assume that a general fiber is cylindrically shaped. Furthermore, in the high-resolution scans acquired the grey value profile of the fibers exhibited a clear maximum at their centers. Moreover, all fibers of a common class usually have constant and previously known diameters [5]. As a consequence, these characteristic features can be exploited by using a model-based segmentation approach. The segmentation algorithm itself is modeled as a multistep process. Firstly, the whole image is filtered and reduced by a closing operation in order to achieve a good fiber separation in the image data. Then, the image is scanned for fiber-center voxels by the means of a discrimination function based on eigenvalue analysis. The detected center points are then used as starting seeds for the tracing algorithm. Model-based segmentation of a center-axis representation is performed by tracing fiber-center points along the direction determined during eigenvalue analysis.
Using the a-priori known radius of the fibers, a segmentation mask is generated in order to remove the corresponding fiber from the input data. These steps, as explained in detail below, are repeated until the input dataset is fiber-free, that is the algorithm cannot find any remaining cylindrical structures in the image data. Finally, the length of each fiber can be determined and a distribution graph can be created.
3.1. Preprocessing
One major problem for the automatic segmentation method is that the fibers contained within a scanned product sample are usually tightly packed (Figure 2). Therefore, it is difficult to apply standard segmentation algorithms, such as region growing [7], since fiber borders may be partly unclear and unwanted flooding may occur. It is, however, possible to preprocess the data so that the edges of the single fibers can be greatly enhanced.
In order to enhance the fiber borders, a morphological erosion filter [7] is applied to the original image  which yields the image
which yields the image  . As a consequence, dark image areas, such as fiber borders, become enlarged in
. As a consequence, dark image areas, such as fiber borders, become enlarged in  . Subsequently, the work image
. Subsequently, the work image  is created by subtracting the eroded image from the original image, that is
is created by subtracting the eroded image from the original image, that is

The result of this operation is shown in Figure 3. It can be observed that single fiber borders show more contrast after the filtering procedure. However, another result of this operation is that fibers which lie close together are now merged to a single fiber in the image. Thereby, fibers are lost during the preprocessing step. Since the original image is processed repeatedly, however, the lost fibers will be detected in a subsequent pass. All of the following operations are carried out exclusively on the work image  .
.
3.2. Center Point Determination
For the segmentation of fiber structures from the image, starting seed points have to be determined. Therefore, image voxels have to be checked whether they belong to a fiber or not. Frangi et al. [8] presented a discrimination function for model-based shape extraction on 3D data, which allows for the association of voxel grey values to estimated shapes.
Originally applied to magnetic resonance image data, it turns out that this model applies well to the extraction of cylindrical shapes from CT data. The discrimination function is based on an eigenvalue analysis of the structure that is to be segmented. For each voxel, the Hessian matrix containing the partial second order derivatives of the data is computed as

Since the Hessian is a symmetric matrix, it can be rearranged to yield

This order facilitates the calculation of the eigenvalues and eigenvectors of this matrix. We have

where  is the matrix containing the eigenvectors
is the matrix containing the eigenvectors  ,
,  and
and  as its columns and
as its columns and  are the eigenvalues corresponding to the eigenvectors. For the numerical solution of these equations, the reader is referred to [9].
are the eigenvalues corresponding to the eigenvectors. For the numerical solution of these equations, the reader is referred to [9].
The eigenvalues of the Hessian calculated from the image voxel data contain information about the gray value change in the image neighborhood. Since for cylindrical shaped objects a specific change pattern is likely, this analysis allows for the determination of the starting seed points. Moreover, since the eigenvectors belonging to the eigenvalues of the voxel span an orthogonal coordinate frame, the direction and extent of the fiber can be estimated.
In [8], an overview of different shape interpretations based on the computed eigenvalues is given. For example, finding all eigenvalues to be of high magnitude and positive value indicates a spherical shape. For the purpose of fiber extraction, the most practical combination is the one given for bright tubular structures and is denoted as  for the three eigenvalues
for the three eigenvalues  . Hence,
. Hence,  is expected to be of low magnitude, whereas
is expected to be of low magnitude, whereas  and
and  should expose high magnitude and should be negative.
should expose high magnitude and should be negative.
The relation of the cylindrical structure to the eigenvectors of the Hessian is shown in Figure 4. It can be seen that high values for the eigenvalues  and
and  are associated with a high gray value change in the direction of the cylinder boundary. Consequently, for the image data this indicates a high gradient magnitude towards the borders which is typical for the expected shape.
are associated with a high gray value change in the direction of the cylinder boundary. Consequently, for the image data this indicates a high gradient magnitude towards the borders which is typical for the expected shape.
In order for a voxel to be located inside a cylindrical structure, the following criteria have to be met.
-
(1)
If
 , then
, then 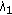 should be as small as possible (
should be as small as possible ( would be ideal),
would be ideal), -
(2)
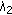 and
and 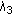 should have great magnitude and should be almost equal.
should have great magnitude and should be almost equal.
These properties can be combined into a discrimination function introduced in [8]

with

where

The parameters  , and
, and  can be used to tune the sensitivity of the function to deviations. For the ideal fiber, the maximum of
can be used to tune the sensitivity of the function to deviations. For the ideal fiber, the maximum of  is reached at the fiber center, while its value decays smoothly towards the border of a cylindrical structure. Consequently, this discriminator can be used to detect image voxels which exhibit the greatest likelihood of belonging to a fiber center. These points are then used as starting seeds for the model-based fiber tracing.
is reached at the fiber center, while its value decays smoothly towards the border of a cylindrical structure. Consequently, this discriminator can be used to detect image voxels which exhibit the greatest likelihood of belonging to a fiber center. These points are then used as starting seeds for the model-based fiber tracing.
Since performing eigenvalue analysis and evaluating the discrimination function for each voxel is computationally very expensive, our implementation includes some optimizations. Firstly, only relevant voxels are taken into account when carrying out the calculations, that is voxels whose grey values exceed a predefined threshold  . This approach is useful, as every dataset contains many elements which cannot be part of a fiber, for example background voxels and low valued image noise. Furthermore, since the eigenvalue analysis of the image data is an independent process for each individual volume element, this part of the algorithm is ideally suited for a parallel implementation. Consequently, it was implemented running on a high-end consumer graphics card using NVIDIA's CUDA technology [10].
. This approach is useful, as every dataset contains many elements which cannot be part of a fiber, for example background voxels and low valued image noise. Furthermore, since the eigenvalue analysis of the image data is an independent process for each individual volume element, this part of the algorithm is ideally suited for a parallel implementation. Consequently, it was implemented running on a high-end consumer graphics card using NVIDIA's CUDA technology [10].
3.3. Fiber Tracing
Having detected possible fiber center point candidates, the algorithm starts the tracing process in order to extract a centerline from the fibers. Since the fiber shape is known a-priori, a model-based cylinder approximation scheme is used. For this purpose, one candidate is selected as a starting point and the fiber is traced along the minimum eigenvector  in both, positive and negative, directions. As known from previous analysis, this vector is directed along the central axis of the cylindrical structure (Figure 4).
in both, positive and negative, directions. As known from previous analysis, this vector is directed along the central axis of the cylindrical structure (Figure 4).
As a result of the fiber tracing, a center point list is generated. Subsequently, the remaining two eigenvectors and the generated center points can be used in order to segment a circular shape (Figure 5). Using the remaining eigenvectors as a coordinate frame basis, all voxels within the circle centered at the center point and the a priori known fiber radius are segmented.
Since the radius of the fibers is material dependent and known beforehand, this segmentation approach is very robust to the presence of image noise on the fiber borders. Once a fiber is fully segmented, it is used as a mask on the original data in order to remove it from the image entirely. The process is repeated until no more fibers can be found in the image. However, due to the nature of the data, there are a few special cases that have to be dealt with, namely crossing fibers and partial fiber segmentation.
3.3.1. Crossing Fibers
When two or more fibers are overlapping within the image data (Figure 6), one or more voxels usually belong to several different fibers. As a consequence, a sudden change of direction during tracing along the minimum eigenvector is very likely. Hence, this results in a wrong fiber segmentation. In order to solve this issue, the angle between two consecutive direction vectors of fiber center points is restricted to be lower than  . This ensures an approximate
. This ensures an approximate  -continuity of the extracted fiber centerline. If the angle between consecutive center point candidates is found to lie above this threshold, the neighborhood of this voxel is searched for a better fitting one and the tracing is continued in the detected direction.
-continuity of the extracted fiber centerline. If the angle between consecutive center point candidates is found to lie above this threshold, the neighborhood of this voxel is searched for a better fitting one and the tracing is continued in the detected direction.
Furthermore, if a voxel is encountered that allows more than one propagation direction, it is again added to the seed point list. Thereby, the voxel is not marked as already segmented and can be reused while tracing the crossing fiber. If no adequate continuation direction is found, the tracing process stops. This can lead to partial fiber segmentation, another possible problem.
3.3.2. Partial Fiber Segmentation
Due to the imposed continuity restriction or image noise, it is possible that a fiber is only partially segmented (Figure 7). Consequently, during the tracing process, the condition of the discrimination function will not be satisfied anymore and the algorithm terminates. As a direct result, gaps within a single fiber may occur. Another possibility is that a previously partially segmented fiber gets completely segmented when starting a subsequent iteration at a different seed point. However, this would lead to a double detection of the fiber, which is also not desirable.
In order to solve this problem, a binary volume is created during fiber tracing. For each successfully segmented voxel, the bit at the corresponding position in the binary volume is set. Furthermore, during the tracing process, each new center voxel which is about to be segmented is checked against this binary volume. If it is already contained in the volume, the corresponding position is marked as a critical point and tracing in the current direction terminates. Once a fiber has been extracted, it is checked for critical points. If it contains a critical point, a search on the already extracted fibers is started for the ones containing the same critical point. If one or more fibers containing equal critical points are found, they are merged in order to create a single fiber mask (Figure 8).
Having extracted all fibers from the dataset, their length computation is straightforward. Since the number of center points is known and the voxel size is isotropic, in the case of axis-aligned center points a simple calculation yields

where  is the number of voxels of the fiber
is the number of voxels of the fiber  and
and  is the voxel size.
is the voxel size.
4. Results
For the evaluation of the presented method, two types of data were used. First of all, artificial test datasets were created. They contained varying types of fibers with different densities and lengths. The major advantage of this data type was that the length of each individual fiber was known beforehand and thus allowed an exact evaluation of the produced results.
Moreover, the algorithm was also evaluated on CT scans of real plastic components. Two of them will be presented in this paper. The first component was built of straight and long cylindrical fibers, approximating the ideal fiber very closely. The second dataset, however, was more difficult to deal with. It contained mostly short, curved, and heavily overlapping fibers. Nevertheless, good segmentation results were achieved in all cases.
4.1. Artificial Test Data
Three datasets containing ideal fiber models were created for evaluation (Figure 9). In order to simulate a real CT scan, random noise was added to the image data before processing.
During the detection phase, all fibers from the test data were found and have been segmented correctly. The correlation with the known results is very high in all cases, as shown in Table 1. In summary, the accuracy of the detection process over the three test cases was about  . Due to the presence of the artificial image noise, the small detection error is tolerable. Tests without addition of the extra noise yielded a fiber-length correlation of
. Due to the presence of the artificial image noise, the small detection error is tolerable. Tests without addition of the extra noise yielded a fiber-length correlation of  .
.
4.2. Real Test Data
From the evaluation on real fiber reinforced polymer components, two selected examples are presented. 3D and slice views are shown in Figures 10 and 13, respectively. Dataset one had a dimension of  in
in  ,
,  and
and  directions and an isotropic voxel size of
directions and an isotropic voxel size of  . As can be obtained from the figures, the fibers in the component exhibit a mostly straight cylindrical structure. Moreover, the fibers are very long with respect to the size of the dataset.
. As can be obtained from the figures, the fibers in the component exhibit a mostly straight cylindrical structure. Moreover, the fibers are very long with respect to the size of the dataset.
The dimensions of dataset two were  with an isotropic voxel size of
with an isotropic voxel size of  . The fibers in this component are less tightly packed, shorter in size with respect to the dataset size and they exhibit a curved structure which indicates a more problematic segmentation task for the presented algorithm.
. The fibers in this component are less tightly packed, shorter in size with respect to the dataset size and they exhibit a curved structure which indicates a more problematic segmentation task for the presented algorithm.
The segmentation results of the real product samples have been evaluated by manual inspection of the dataset, since pyrolizing the sample components was not yet possible. However, the results of applying our algorithm to dataset one were found to be very good as can be seen in Figure 11. All relevant fibers have been segmented correctly in terms of size and radius. Therefore, it is reasonable to assume that the resulting length distribution is correct within acceptable statistical deviations. Figure 12 shows a plot of the calculated length distribution. As expected, the majority of the detected fibers are very long ( ), with only a few fibers to be found in the low to mid-sized range.
), with only a few fibers to be found in the low to mid-sized range.
On dataset two, most of the fibers were also segmented correctly (Figure 14). This indicates that the model-based segmentation approach is robust even in the presence of curved fibers. However, the number of gaps between the fibers on this type of dataset is higher than for the straightforward case. The resulting length distribution of dataset two is shown in Figure 15. As expected, the majority of the detected fibers are very short with respect to the dataset size (up to  ).
).
5. Conclusion
In this paper, a novel, model-based approach for the automatic detection, segmentation, and length distribution calculation of fibers in CT data of fiber reinforced polymers was presented. Since fiber length distribution within the material is essential for the stability of an assembly, having a non-destructive evaluation method is highly desirable.
The presented approach uses a segmentation scheme which was shown to be robust even in the presence of curved fibers and image noise. The algorithm is also able to handle tightly packed and crossing fibers, though the accuracy suffers in these cases, as not all fibers may be detected fully or gaps may occur within single fibers. In order to estimate a systematic error in this situations, more datasets have to be investigated and the automatic results have to be compared to the outcome of a pyrolysis analysis. Moreover, current  scanning devices are still restricted to scanning small sample sizes only, which currently limits the practical applicability of this method.
scanning devices are still restricted to scanning small sample sizes only, which currently limits the practical applicability of this method.
However, the results show that the presented algorithm can achieve a reasonably good segmentation and thus can act as a basis for further research on this topic. Further research will include the acquisition of reference data by pyrolizing the investigated sample components. Moreover, distribution statistics and error measurements of real samples have to be included in the evaluation of our material testing approach in order to devise a systematic error measurement. These steps are important for an intense evaluation and will be carried out in the near future.
With the current advent of high-resolution  scanning devices that are capable of taking images of bigger structures, the presented method could become a valuable tool for broad inspection of varying material. This could be especially useful in industries where material function is vital and undetected wearout could have severe impacts.
scanning devices that are capable of taking images of bigger structures, the presented method could become a valuable tool for broad inspection of varying material. This could be especially useful in industries where material function is vital and undetected wearout could have severe impacts.
References
Hug AMA, Azaiez J: Effects of length distribution on the steady shear viscosity of semiconcentrated polymer-fiber suspensions. Polymer Engineering and Science 2005, 45(10):1357-1368. 10.1002/pen.20415
Neitzel M, Mitschang P: Handbuch Verbundwerkstoffe. Carl Hanser, München, Germany; 2004.
Fu S-Y, Yue C-Y, Hu X, Mai Y-W: Characterization of fiber length distribution of short-fiber reinforced thermoplastics. Journal of Materials Science Letters 2001, 20(1):31-33. 10.1023/A:1006750328386
Smallman R, Bishop R: Modern Physical Metallurgy and Materials Engineering. Butterworth-Heinemann; 1999.
Erhard G: Designing with Plastics. Hanser Gardner; 2006.
Washer G, Blum F Jr.: Raman spectroscopy for the nondestructive testing of carbon fiber. Research Letters in Materials Science 2008, 2008:-3.
Pratt W: Digital Image Processing. 2007.
Frangi AF, Niessen WJ, Hoogeveen RM, van Walsum T, Viergever MA: Modelbased quantitation of 3-d magnetic resonance angiographic images. IEEE Transactions on Medical Imaging 1999, 18(10):946-956. 10.1109/42.811279
Press WH, Teukolsky SA, Vetterling WT, Flannery BP: Numerical Recipes: The Art of Scientific Computing. 2007.
Fatica M, Luebke D, Buck I, et al.: High-performance computing with cuda. SUPERCOMPUTING Tutorial, 2007
Acknowledgments
The authors are thankful to T. Potyra and M. Reif (Fraunhofer ICT) for providing the samples used for evaluation. This paper was cofinanced by the European Union and the Free State of Bavaria, Germany.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Teßmann, M., Mohr, S., Gayetskyy, S. et al. Automatic Determination of Fiber-Length Distribution in Composite Material Using 3D CT Data. EURASIP J. Adv. Signal Process. 2010, 545030 (2010). https://doi.org/10.1155/2010/545030
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/545030

 .
.



 , then
, then 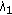 should be as small as possible (
should be as small as possible ( would be ideal),
would be ideal),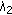 and
and 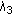 should have great magnitude and should be almost equal.
should have great magnitude and should be almost equal.









