Abstract
Compressive sensing (CS) is mainly concerned with low-coherence pairs, since the number of samples needed to recover the signal is proportional to the mutual coherence between projection matrix and sparsifying matrix. Until now, papers on CS always assume the projection matrix to be a random matrix. In this paper, aiming at minimizing the mutual coherence, a method is proposed to optimize the projection matrix. This method is based on equiangular tight frame (ETF) design because an ETF has minimum coherence. It is impossible to solve the problem exactly because of the complexity. Therefore, an alternating minimization type method is used to find a feasible solution. The optimally designed projection matrix can further reduce the necessary number of samples for recovery or improve the recovery accuracy. The proposed method demonstrates better performance than conventional optimization methods, which brings benefits to both basis pursuit and orthogonal matching pursuit.
which can be sparsely represented over a fixed dictionary 
that is assumed to be redundant 
. Accordingly, the signal can be described as
is the coefficient vector which represents 
on 
and 
. The 
norm used here simply counts the number of nonzero element in 
.
inner products between 
and a collection of vectors 
as 
. Arrange the measurements 
in an 
vector 
and the sampling vectors 
as rows in an 
matrix 
, then 
can be written as
can be reconstructed from 
by exploring its sparse expression, that is, among all possible 
that satisfies 
, seek the sparsest. If this representation coincides with 
, a perfect reconstruction of the signal in (1) is gotten. This reconstruction requires the solution of
is defined as the equivalent dictionary.
is drawn at random except the one by Elad [
-averaged mutual coherence between 
and 
, where 
is fixed. Although the reconstruction performance can be obviously improved, the method is time-consuming because it needs many iterative steps to achieve good performance. Some large mutual coherence values that are not present in the original Gram matrix are also created, which ruin completely the worst case guarantees of the reconstruction algorithms. Instead of targeting on the 
-averaged mutual coherence between 
and 
, in [
as orthogonal as possible, or equivalently, making the Gram matrix as closely as possible to identity matrix. The method is much faster than Elad's but the reconstruction performance is not very good because 
is overcomplete and it could not be an orthogonal basis.
are zero or they can be discarded without much loss of information. Incoherence means, in (2), the projection matrix 
and the sparsifying matrix 
should be as incoherent as possible. A possible measure of coherence between 
and 
is given by the inner products of different columns in 
[
which is computed after normalizing each column of 
. The off-diagonal entries of 
are the inner products that appear in (4). Mutual coherence is the off-diagonal entry with largest magnitude.
is a positive constant, 
is the sparsity level of signal, and 
is the dimension. It is obvious to see that the smaller the coherence, the fewer samples are needed [
is necessary the sparsest solution such that 
and the reconstruction algorithms are guaranteed to succeed in finding the correct 
[
and 
. With the properties of 
, there is a sensible reason to design the projection matrix in a way that minimizes the mutual coherence 
which may lead to better performance of reconstruction algorithms.
is fixed while 
can be arbitrary is considered. Hence, the object is to optimize 
that will minimize the mutual coherence 
. After reviewing the former related work, the proposed algorithm is introduced.
-averaged mutual coherence which reflects the average behavior. The 
-averaged mutual coherence of 
is defined as the average of all absolute and normalized inner products between different columns in 
(denoted as 
) that are above 
. Formally
with respect to 
, assuming that 
and the parameter 
are fixed and known. In this algorithm, the main object is the reduction of the absolute inner products 
that are above 
. The Gram matrix of the normalized equivalent dictionary is computed and the values above 
are "shrinked" by multiplying with 
. In order to preserve the order of the absolute values in the Gram matrix, entries in 
with magnitude below 
but above 
are "shrinked" by a small amount using the following function:
and find the matrix 
that could best describe the squared root of the obtained Gram matrix. The process could be realized using SVD. The details can be found in [
-averaged mutual coherence between 
and 
, this method addressed the problem by making any subset of columns in 
as orthogonal as possible, or equivalently, making the Gram matrix as close as possible to an identity matrix. Their approach was carried out as follows.
that makes the Gram matrix as close as possible to identity matrix
on the left and 
on the right, it becomes
which is
, they finally formulated the problem to minimize the following function with respect to 
:
be the Gram matrix of 
. The mutual coherence of 
is the maximum absolute value of the off-diagonal entry of 
, supposing the columns of 
are normalized. For such 
, if the magnitudes of all off-diagonal entries of 
are equal, 
has minimum coherence [
, the mutual coherence of 
is defined as
is called ETF when there is a constant 
that
uniform frames, it is the solution of
, the existence of an ETF and its Gram matrix, Strohmer showed that 
is lower bounded by
be the set of Gram matrices of all 
ETF. If 
, then the diagonal elements and the absolute values of the off-diagonal elements of 
are one and 
, respectively. A nearness measure of 
to the set of ETF can be defined as the minimum distance between the Gram matrix of 
and 
. To minimize the distance of a dictionary to ETF, it needs to solve
is defined as the maximum absolute value of the elements in the matrix. Instead, it is better to use a different norm space which simplifies the problem. An advantage of using 
in the given problem is that it considers the errors of all elements. Therefore it forms the following formulation:
is Frobenius norm. This is a nonconvex optimization problem in general. It might have a set of solutions or have no solution. Extend 
to a convex set 
, which is not empty for any 
,
with 
, it gives the following optimization problem:
. A point between the current solution and the projection on 
is chosen, that is because after being projected onto 
, the structure of the Gram matrix changes significantly and the selection of a new point in the following step is very difficult. After performing alternating minimization, the optimized projection matrix can be constructed from the output Gram matrix with a rank revealing QR factorization with eigenvalue decomposition. The details can be found in [
, sparsifying matrix 
, and equivalent dictionary 
, iterative steps 
, denote the element of 
as 
, that is,
to update the Gram matrix
using QR factorization with eigenvalue decomposition
before and after optimization is considered. Figure 
which can make the equivalent dictionary as close as possible to an ETF. This better behavior can further reduce the necessary samples for recovery and improve the recovery performance.
before and after optimization.
.
and synthesize 
test signals 
by generating 
sparse vectors 
of length 
each, and computing for all 
. All representations are built using the same cardinality 
.
.
, create a random projection matrix 
and apply it to the signals, obtaining 
, for all 
, Compute the equivalent dictionary 
.
.
subject to 
. Test the error 
. Measure the average error rate—a reconstructionwith a mean squared error above some threshold is considered as a reconstruction failure.
.
was used. This size was chosen since it enabled the CS performance evaluation in reasonable time. 
sparse vectors were generated of length 
with cardinality 
. The nonzero's locations were chosen at random. These sparse vectors were used to create the test signals with which the CS performance was evaluated. CS performance was tested with varying values of 
. The relative error rate was evaluated as a function of 
for both OMP and BP before and after the optimization. Each point in the graph represents an average performance, accumulated over a possible varying number of experiments. While every point was supposed to present an average performance over 
signals, in cases where more than 300 errors was accumulated, the test stopped and the average so far was used instead. This was done to reduce the overall runtime.
increases and in this experiment, BP outperforms OMP. Also, as expected, all the optimization methods lead to improved performance of CS. For some values of 
, the performance is improved by 10 : 1 for BP and 100 : 1 for OMP. The optimization method proposed by us outperforms both Elad's method and Duarte-Carvajalino and Sapiro's method. For some values of 
, our method improves the CS performance by 5 : 1 than Elad's method and even 10 : 1 than Duarte-Carvajalino and Sapiro's method for OMP. The improvement for BP is smaller than OMP, about 2 : 1 for some values of 
.
was fixed and 
was changeable. From Figures 
increases. That is because as 
increases, more measurements are needed to achieve the same CS performance. Also, as expected, the CS performance is improved after using the optimization methods mentioned above with both BP and OMP. The improvement is much larger with OMP than that with BP. It is almost 100 : 1 for some values of 
with OMP. The CS performance is obviously improved using the proposed optimization method than both Elad's method and Duarte-Carvajalino and Sapiro's method. It is about 4 : 1 to Elad's method with OMP. With respect to BP, when 
is small, the improvement is larger and when 
increases, the CS performance is almost the same for all the optimization methods.
was varied while proportionally updating measurements 
, dictionary dimension 
and signal cardinality 
with it. The object was to get a better indication to the asymptotic performance as studied in [
using BP.
using OMP.
, (b) recovered using optimized 
by Elad's method, and (c) recovered using optimized 
by our proposed method.
patches reconstructed from their noisy projections (5% level of noise).
is set to be 15 and the sparsifying matrix to be DCT. The reconstruction algorithm used is OMP. From the pictures above, it is obvious to see that the recovery performance is improved for both the optimization methods. The Elad's method can improve PSNR about 1 db than using random 
, and the proposed method in this paper can improve about 0.5 db than Elad's method. If larger number of measurements is used for recovery, the reconstruction performance could be better, but it is time-consuming.
and 
based on ETF design. The experimental results demonstrated that the optimally designed projection matrix indeed lead to a better CS performance, not only improvement of the reconstruction accuracy but also reduction in the necessary number of samples for recovery. It also demonstrated that after optimizing the projection matrix using the proposed method, the CS performance was greatly improved than using random projection matrix and the already existed optimization methods.
) How to perform the proposed method when the signals are of high dimension. (
) Whether there is a more direct method to address the problem which may be easier.
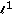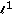minimization. Proceedings of the National Academy of Sciences of the United States of America 2003, 100(5):2197-2202. 10.1073/pnas.0437847100