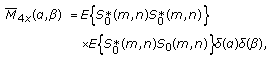- Research Article
- Open access
- Published:
Two-Dimensional Harmonic Retrieval in Correlative Noise Based on Genetic Algorithm
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 569371 (2010)
Abstract
We propose a niche Genetic algorithm (GA) for the two-dimensional (2D) harmonic retrieval in the presence of correlative zero-mean, multiplicative, and additive noise. Firstly, we introduce a 2D fourth-order time-average moment spectrum which has extremum values at the harmonic frequencies. On this basis, the problem of harmonic retrieval is treated as a problem of finding the extremum values for which the niche GA is resorted. Utilizing the global searching ability of the GA, this method can improve the frequency estimation performance. The effectiveness of the proposed algorithm is demonstrated through computer simulations.
1. Introduction
2D harmonic retrieval is of interest in signal processing such as sonar, radar, geophysics, and radio astronomy. In the case of additive noise, some high-resolution techniques such as the 2D MUSIC [1], the 2D MEMP [2], and the 2D ESPRIT method [3] have been developed from their 1D versions. Of these algorithms, the ESPIRIT algorithm is more effective as it does not require to search for the peak value in a 2D space. Different from the above methods considering white noise, in the presence of colored Gaussian noise, Ibrahim and Gharieb [4, 5] have presented some methods based on fourth-order cumulants since the cumulants are insensitive to Gaussian noise while they contain frequency and phase information.
Under certain circumstances, the amplitudes of the received harmonic signals are random since they are usually corrupted by multiplicative noise. For example, multiplicative noise is encountered in underwater acoustic applications due to the dispersive medium [6, 7], and random amplitude modulation occurs in Doppler-radar signals when the target scintillates or when the point target assumption is no longer valid [8]. Techniques based on cyclic statistics have been proposed to estimate the 2D harmonic frequencies in multiplicative noise [9, 10]. However, these methods are based on the assumption that multiplicative and additive noises are mutually independent and mixing.
In practice, the correlation of the multiplicative and additive noise should be considered. In correlative multiplicative and additive noise, Wu and Li [11] has studied the problem of the quadratic nonlinear coupling of 2D harmonics based on 2D third-order time-average moment spectrum. Another two new 2D cyclic statistics are also introduced to estimate the harmonic frequencies in [12, 13], respectively. However, both the methods suffer from a resolution limit and no strategy of searching for the extremum values is discussed. In this paper, we propose a new strategy to improve the frequency estimation performance. Since the fourth-order time-average moment spectrum defined in [13] peaks at the harmonic frequencies, the harmonic retrieval can be treated as finding the extremum values in a 2D space. Utilizing the global searching ability, a GA-based algorithm is presented to estimate the frequencies of 2D harmonic corrupted by correlative multiplicative and additive noise. Simulation examples show that the improved frequency estimation can be achieved.
The organization of the paper is as follows. In Section 2, we introduce a special 2D fourth-order time-average moment spectrum. In Section 3, a GA-based algorithm is proposed to estimate harmonic frequencies. Numerical examples are presented in Section 4, and conclusions are drawn in Section 5.
2. 2D Harmonic Model
Consider a discrete-time  -component 2D harmonics in multiplicative and additive noise model
-component 2D harmonics in multiplicative and additive noise model

where  denotes the
denotes the  th frequency pair and
th frequency pair and  represents the
represents the  th phase.
th phase.  and
and  denote multiplicative and additive noise, respectively. In this paper, the following assumptions are given by
denote multiplicative and additive noise, respectively. In this paper, the following assumptions are given by
-
(AS1)
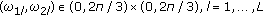 , frequency pairs are mutually unequal and not coupled;
, frequency pairs are mutually unequal and not coupled; -
(AS2)
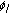 s are deterministic constants in
s are deterministic constants in 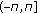 ;
; -
(AS3)
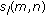 s and
s and 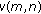 are mutually correlative and stationary stochastic processes with the mean
are mutually correlative and stationary stochastic processes with the mean  and
and 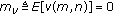 ;
; -
(AS4)
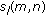 s and
s and 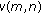 satisfy the so-called cross-mixing condition [12]:
satisfy the so-called cross-mixing condition [12]: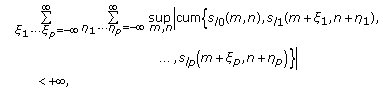 (2)
(2)where
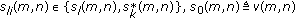 ,
, 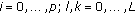 .
.
Note that if the variance  , the model in (1) would become the classical case of harmonics with constant amplitude in additive noise. The first assumption ensures that the fourth-order time-average moment spectrum which will be defined latter peaks at the harmonic frequencies. The second assumption ensures the identifiability of harmonic phases. In the third assumption, without loss of generality, the mean of the additive noise can be assumed to be zero. A nonzero mean can always be estimated consistently via the sample mean and then subtracted from the data. When the mean of multiplicative noise
, the model in (1) would become the classical case of harmonics with constant amplitude in additive noise. The first assumption ensures that the fourth-order time-average moment spectrum which will be defined latter peaks at the harmonic frequencies. The second assumption ensures the identifiability of harmonic phases. In the third assumption, without loss of generality, the mean of the additive noise can be assumed to be zero. A nonzero mean can always be estimated consistently via the sample mean and then subtracted from the data. When the mean of multiplicative noise  , Wang et al. [9] and Yang and Li [10] have presented some effective methods to estimate the harmonic frequencies.
, Wang et al. [9] and Yang and Li [10] have presented some effective methods to estimate the harmonic frequencies.
Generally,  and
and  are always assumed to be mixing and mutually independent [6–10]. In order to describe the correlativity of multiplicative and additive noise, Xu et al. [12] derived the cross mixing condition. If
are always assumed to be mixing and mutually independent [6–10]. In order to describe the correlativity of multiplicative and additive noise, Xu et al. [12] derived the cross mixing condition. If  and
and  are mixing and mutually independent, they are also cross mixing. On the contrary, if
are mixing and mutually independent, they are also cross mixing. On the contrary, if  and
and  are cross mixing, they must be mixing, but it doesn't mean that they are mutually independent. The correlativity of multiplicative and additive noise can be described by cross-mixing condition. The cross-mixing property implies that samples of the processes that are well separated in time can be regarded as approximately independent [14]. Under the cross-mixing condition, time averages of the cyclic statistics converge in the mean-square sense to their sample averages. In model (1), if
are cross mixing, they must be mixing, but it doesn't mean that they are mutually independent. The correlativity of multiplicative and additive noise can be described by cross-mixing condition. The cross-mixing property implies that samples of the processes that are well separated in time can be regarded as approximately independent [14]. Under the cross-mixing condition, time averages of the cyclic statistics converge in the mean-square sense to their sample averages. In model (1), if  and
and  are cross-mixing, the observed signal
are cross-mixing, the observed signal  is cyclostationary, and the sample estimates of its cyclic statistics converge in the sense of mean square and are asymptotically normal [15].
is cyclostationary, and the sample estimates of its cyclic statistics converge in the sense of mean square and are asymptotically normal [15].
For notational simplicity, let  ,
,  . Then (1) is given by
. Then (1) is given by

Definition 1.
The special fourth-order time-average moment of  is defined as
is defined as

where  .
.
Definition 2.
The special fourth-order time-average moment spectrum is defined as

Theorem 1.
From [13], the fourth-order time-average moment spectrum of  corresponding to (5) can be obtained by
corresponding to (5) can be obtained by

where  is Kronecker function. Equation (6) contains harmonic frequency information. This relation will be proved in the appendix.
is Kronecker function. Equation (6) contains harmonic frequency information. This relation will be proved in the appendix.
From (6),  is unequal to zero only if
is unequal to zero only if  , or
, or  . According to Assumption 1,
. According to Assumption 1,  , the number of the obtained greatest maxima of
, the number of the obtained greatest maxima of  should be L rather than
should be L rather than  in the
in the  plane.
plane.
From [16],  can be estimated using single record, namely,
can be estimated using single record, namely,

Further, we have

where a.s. representsalmost sure convergence which is uniform in  and
and  . Equation (8) means that the single record estimator
. Equation (8) means that the single record estimator  is strongly consistent. Alternatively, we can estimate the harmonic frequencies by searching for
is strongly consistent. Alternatively, we can estimate the harmonic frequencies by searching for  greatest maxima of
greatest maxima of  in the
in the  plane. Consequently, the frequency estimation of 2D harmonics can be treated as finding the extremum values of binary function. In this paper, the GA is proposed to seek
plane. Consequently, the frequency estimation of 2D harmonics can be treated as finding the extremum values of binary function. In this paper, the GA is proposed to seek  local optimum solutions.
local optimum solutions.
3. Genetic Algorithm Realization
GA is nowadays one of the most popular stochastic optimization techniques which is inspired by natural genetics and biological evolutionary process. It is supposed that individuals with more adaptability in current generation would have better capability of survival and breeding in the next generation. One of the most important advantages of GA is that it can make use of the limited searching processes to automatically find the optimal or near-optimal result in the solution space. Compared with the classical optimization algorithms, GA has such features as follows [17].
-
(1)
GA starts from multipoints instead of one point. Thereby, it could effectively prevent the searching processes from stopping in local optimum solutions.
-
(2)
The optimization rule of GA is varied. It is determined by probability.
-
(3)
The fitness is calculated only from object function. No other information is necessary.
-
(4)
It automatically seeks the optimal result in the whole solution space.
-
(5)
The calculation is relatively simple.
GA evaluates a population and generates a new one iteratively, with each successive population referred to as a generation. Assume the current generation  is
is  . After applying a set of genetic operations, the GA generates a new generation
. After applying a set of genetic operations, the GA generates a new generation  based on the previous generation. Three basic operators are used to manipulate the genetic composition of a population: selection, crossover, and mutation [17].
based on the previous generation. Three basic operators are used to manipulate the genetic composition of a population: selection, crossover, and mutation [17].
The detailed implementation of the proposed method is given as follows.
 Fitness Function
Fitness Function
In order to perform GA, it is very important to define an appropriate fitness function. In GA, the probability of individual survival to the next generation depends on its fitness value. The greater the fitness value of an individual, the greater probability it has to inherit to the next generation. In this paper, the fitness function is constructed by the operation of getting the absolute value on the nonlinear function (7)

where  is the observed signal.
is the observed signal.
 Generation of the Initial Group
Generation of the Initial Group
Commonly in GA, the initial population is randomly generated. The real-coded GA is adopted in this paper. The length of chromosome graph is set as 3. The first two genes denote the frequency pairs and the third gene denotes the fitness value.
The performance of GA is influenced heavily by the population size. GA may run the risk of serious under-covering of the solution space and result in a local optimum when the population size is relatively small, whereas GA would increase the computational load when the population size is relatively large. Consequently, the population size should be chosen according to the problem scale.
 Selection
Selection
The operation is to choose the good individual and get rid of the bad one from the group. The larger the fitness, the larger probability the individual has to be selected. To achieve this, the roulette wheel selection is used. The fitness of the  th individual is denoted as
th individual is denoted as  . The selection probability of the
. The selection probability of the  th individual is computed as
th individual is computed as  . At the same time, we reserve the best individual to the next population.
. At the same time, we reserve the best individual to the next population.
 Crossover
Crossover
The crossover is to exchange some parts of an individual with corresponding parts of another. The crossover is performed in the following way. Assume that  and
and  are pairs of parent chromosome, whether to crossover or not depends on the crossover probability
are pairs of parent chromosome, whether to crossover or not depends on the crossover probability  . The result of crossover is
. The result of crossover is

where  is a uniformly distributed random number in
is a uniformly distributed random number in  .
.
 Mutation
Mutation
The mutation operator adopts "Nonuniform Mutation" [18]. Compared with the classical uniform mutation operator, this operator has the advantage of making fewer changes on the genes with the number of generations increasing. This property makes the tradeoff between exploration and exploitation. It is more favorable to have exploration in the early stages of the algorithm, while exploitation becomes of greater importance when the obtained solution is closer to the optimal solution. The mutation can be completed in the following way: assuming  is the
is the  th component of the individual
th component of the individual  , the mutation probability
, the mutation probability  determines whether to mutate or not. The result of mutation is
determines whether to mutate or not. The result of mutation is

where positive number  controls the dependence degree of random fluctuation to evolution number
controls the dependence degree of random fluctuation to evolution number  and
and  are uniformly distributed as random numbers on the interval
are uniformly distributed as random numbers on the interval  .
.  is the largest evolution number.
is the largest evolution number.
 Condition to Terminate the GA Iterations
Condition to Terminate the GA Iterations
When the number of generation reaches  , the iterations would be terminated.
, the iterations would be terminated.
In this paper, we seek all the optimal solutions of nonlinear function  , including local optimal solutions and global optimal solutions. However, the simple genetic algorithm is unable to get all optimal solutions. According to the niche phenomenon in nature [19, 20], a niche GA-based method is proposed to estimate harmonic frequencies. A niche in nature can be viewed as a subspace in the environment. Accordingly, a niche is commonly thought as a peak of the fitness function. The niche techniques gather the individuals on several peaks of fitness function in the population according to genetic likeness. The structure of a niche is implemented by decreasing the fitness value of the individual. The concrete method is implemented by calculating the Euclidean distance between parent individual and arbitrary other child individual and then judging whether two individuals are in the circle defined by estimating niche radius
, including local optimal solutions and global optimal solutions. However, the simple genetic algorithm is unable to get all optimal solutions. According to the niche phenomenon in nature [19, 20], a niche GA-based method is proposed to estimate harmonic frequencies. A niche in nature can be viewed as a subspace in the environment. Accordingly, a niche is commonly thought as a peak of the fitness function. The niche techniques gather the individuals on several peaks of fitness function in the population according to genetic likeness. The structure of a niche is implemented by decreasing the fitness value of the individual. The concrete method is implemented by calculating the Euclidean distance between parent individual and arbitrary other child individual and then judging whether two individuals are in the circle defined by estimating niche radius  . Compare with simple GA, niche GA can find more than one optima during evolution. The basic steps of the algorithm are given as follows.
. Compare with simple GA, niche GA can find more than one optima during evolution. The basic steps of the algorithm are given as follows.
-
(1)
Set the generation number
 . Create an initial population which includes
. Create an initial population which includes 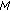 individuals and evaluate their fitness.
individuals and evaluate their fitness. -
(2)
Sort the population according to their fitness and memorize the first
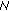 individuals.
individuals. -
(3)
Produce a new population through selection, crossover and mutation.
-
(4)
Evaluate the fitness of every new individual.
-
(5)
Keep the
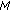 individuals from step 3 and
individuals from step 3 and 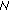 memorial individuals from step 2. Evaluate the distanced between each two of them. Introduce a penalty
memorial individuals from step 2. Evaluate the distanced between each two of them. Introduce a penalty 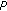 to the individual with lower fitness when
to the individual with lower fitness when 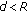 .
. -
(6)
Combine the
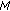 individuals with the
individuals with the  individuals. Sort the
individuals. Sort the  individuals according to their fitness. Save the first
individuals according to their fitness. Save the first 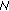 individuals and the first
individuals and the first 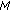 individuals.
individuals. -
(7)
Set
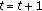 and repeat steps 3–6 until
and repeat steps 3–6 until 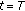 .
.
4. Simulations
Computer simulations are presented here to illustrate the main aspects of this paper. In all simulations, we generate (1) with  , and
, and  . The multiplicative noises are generated by
. The multiplicative noises are generated by

where the mean  . The additive noise
. The additive noise  is also generated by
is also generated by  with the mean
with the mean  . The signal-to-noise ratio (SNR) is defined as
. The signal-to-noise ratio (SNR) is defined as

Example 1.
Consider  as white Gaussian noise with the mean
as white Gaussian noise with the mean  and the variance
and the variance  . The fourth-order time-average moment spectrum is computed according to (7). Figure 1 shows
. The fourth-order time-average moment spectrum is computed according to (7). Figure 1 shows  when the SNR is 0 dB and the data size is
when the SNR is 0 dB and the data size is  .
.  which varies with
which varies with  and
and  is plotted in Figure 1(a). It can be observed that there are three obvious peaks. It is shown in Figure 1(b) that three peaks locate at the accurate positions
is plotted in Figure 1(a). It can be observed that there are three obvious peaks. It is shown in Figure 1(b) that three peaks locate at the accurate positions  , and
, and  . Figure 1(c) shows the ten greatest estimated mean of
. Figure 1(c) shows the ten greatest estimated mean of  using the GA from 100 Monte Carlo runs. The
using the GA from 100 Monte Carlo runs. The  -coordinate denotes the index of individuals and the
-coordinate denotes the index of individuals and the  -coordinate denotes the corresponding estimated mean. It can be shown that there is an obvious boundary among the estimated values. The estimated number of harmonics is 3. However, if the SNR is very low, there is no obvious boundary among the estimate values. In this situation, we should estimate the number of harmonics firstly. More detail of estimating the number of harmonics has been presented in [21, 22].
-coordinate denotes the corresponding estimated mean. It can be shown that there is an obvious boundary among the estimated values. The estimated number of harmonics is 3. However, if the SNR is very low, there is no obvious boundary among the estimate values. In this situation, we should estimate the number of harmonics firstly. More detail of estimating the number of harmonics has been presented in [21, 22].
The GA parameters are set as follows. Initial population  , memorial population
, memorial population  , genetic times
, genetic times  , crossover probability
, crossover probability  , mutation probability
, mutation probability  , mutation control parameter
, mutation control parameter  , niche destining distance
, niche destining distance  , and individual penalty
, and individual penalty  .
.
In this simulation, the performance of the GA-based and the fourth-order time-average moment spectrum-based (FOTAMS) method [13] is compared. Figure 2 shows the root mean squared errors (RMSEs) on the estimated frequency pairs when the data size is  which are computed as functions of the SNR from 100 Monte Carlo runs. The frequency estimates of the proposed method are more accurate than that of the FOTAMS-based method whatever the SNR is. The RMSEs of the estimated frequency pairs versus the data size
which are computed as functions of the SNR from 100 Monte Carlo runs. The frequency estimates of the proposed method are more accurate than that of the FOTAMS-based method whatever the SNR is. The RMSEs of the estimated frequency pairs versus the data size  at SNR = 0 dB are shown in Figure 3. It is clear that as the data size increases, the estimation accuracy improves. The estimated values of the proposed method are also more accurate than that of the FOTAMS-based method regardless of the data size.
at SNR = 0 dB are shown in Figure 3. It is clear that as the data size increases, the estimation accuracy improves. The estimated values of the proposed method are also more accurate than that of the FOTAMS-based method regardless of the data size.
Example 2.
To illustrate that the proposed method is insensitive to the distribution of the noise,  is assumed to be the i.i.d. white exponential noise with the mean
is assumed to be the i.i.d. white exponential noise with the mean  . Other parameters are the same as that in Example 1. Figure 4 shows
. Other parameters are the same as that in Example 1. Figure 4 shows  with SNR = 0 dB. Similar to Example 1, we can also observe that three obvious peaks locate at the accurate positions
with SNR = 0 dB. Similar to Example 1, we can also observe that three obvious peaks locate at the accurate positions  , and
, and  . Figures 5 and 6 show the RMSEs performance of frequency estimation versus the SNR and the data size, respectively. It is illustrated that the GA estimators also perform better than the FOTAMS estimators.
. Figures 5 and 6 show the RMSEs performance of frequency estimation versus the SNR and the data size, respectively. It is illustrated that the GA estimators also perform better than the FOTAMS estimators.
5. Conclusion
In this paper, a cyclic statistics-based method for frequency estimation of 2D harmonics in correlative multiplicative and additive noise is addressed. Since the 2D fourth-order time-average moment spectrum peaks at the frequencies of harmonic, the problem of harmonic retrieval can be solved by finding the extremum values. Exploiting global searching ability of GA and the niche phenomenon in nature, we propose a niche GA method to estimate harmonic frequencies. This method can improve the estimation accuracy. Simulation results demonstrated the effectiveness of the presented method. Moreover, our method can be extended to the parameter estimation of 2D harmonics under other conditions.
References
Odendaal JW, Barnard E, Pistorius CWI: Two-dimensional superresolution radar imaging using the MUSIC algorithm. IEEE Transactions on Antennas and Propagation 1994, 42(10):1386-1391. 10.1109/8.320744
Hua Y: Estimating two-dimensional frequencies by matrix enhancement and matrix pencil. IEEE Transactions on Signal Processing 1992, 40(9):2267-2280. 10.1109/78.157226
Rouquette S, Najim M: Estimation of frequencies and damping factors by two-dimensional ESPRIT type methods. IEEE Transactions on Signal Processing 2001, 49(1):237-245. 10.1109/78.890367
Ibrahim HM, Gharieb RR: Estimating two-dimensional frequencies by a cumulant-based FBLP method. IEEE Transactions on Signal Processing 1999, 47(1):262-266. 10.1109/78.738268
Gharieb RR: Cumulant-based LP method for two-dimensional spectral estimation. IEEE Proceedings: Vision, Image and Signal Processing 1999, 146(6):307-312. 10.1049/ip-vis:19990743
Giannakis GB, Zhou G: Harmonics in multiplicative and additive noise: parameter estimation using cyclic statistics. IEEE Transactions on Signal Processing 1995, 43(9):2217-2221. 10.1109/78.414790
Dwyer RF: Fourth-order spectra of Gaussian amplitude-modulated sinusoids. Journal of the Acoustical Society of America 1991, 90(2):918-926. 10.1121/1.401958
Besson O, Stoica P: Sinusoidal signals with random amplitude: least-squares estimators and their statistical analysis. IEEE Transactions on Signal Processing 1995, 43(11):2733-2744. 10.1109/78.482122
Wang F, Wang S-X, Dou H-J: Two-dimensional parameter estimation using two-dimensional cyclic statistics. Journal of Electronics 2003, 31(10):1522-1525.
Yang S-Y, Li H-W: Two-dimensional harmonics parameters estimation using third-order cyclic-moments. Journal of Electronics 2005, 33(10):1808-1811.
Wu S, Li H: The analysis of two-dimensional quadratic coupled harmonics in the complex noise based on genetic algorithm. Signal Processing Journal 2006, 22: 635-638.
Xu J, Wang S-X, Wang H: Harmonic retrieval and nonlinear frequency-coupled harmonics in the complex noise. Journal of Electronics 2003, 31: 117-122.
Dou H, Wang S-X, Wang F: Two-dimensional harmonics retrieval in correlative multiplication and additive noise. Proceedings of the 7th International Conference on Signal Processing (ICSP '04), September 2004, Beijing, China 264-268.
Brillinger DR: Time Series: Data Analysis and Theory. Holden-day, San Francisco, Calif, USA; 1981.
Dandawate AV, Giannakis GB: Asymptotic theory of mixed time averages and kth-order cyclic-moment and cumulant statistics. IEEE Transactions on Information Theory 1995, 41(1):216-232. 10.1109/18.370106
Li H, Cheng Q, Yuan B: Strong laws of large numbers for two-dimensional processes. Proceedings of the 4th International Conference on Signal Processing (ICSP '98), October 1998, Beijing, China 43-46.
Goldberg DE: Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley, Reading, Mass, USA; 1989.
Michalewicz Z: Genetic Algorithms + Data Structures = Evolution Programs. 3rd edition. Springer, New York, NY, USA; 1999.
Deb K, Coldberg DE: An investigation of niche and species formation in genetic function optimization. In Proceedings of the 3rd Conference on Genetic Algorithms (ICGA '89), 1989, San Mateo, Calif, USA. Morgan Kaufmann; 42-50.
Zhou M, Sun S: The Theory and Application of Genetic Algorithm. The Press of National Defence and Industry, Beijing, China; 1999.
Yang S, Li H: Estimation of the number of harmonics in multiplicative and additive noise. Signal Processing 2007, 87(5):1128-1137. 10.1016/j.sigpro.2006.10.011
Yang S, Li H: Estimating the number of harmonics using enhanced matrix. IEEE Signal Processing Letters 2007, 14(2):137-140.
Acknowledgments
The authors would like to thank the anonymous reviewers for their constructive comments and suggestions that helped to improve the paper. This work is supported by the National Natural Science Foundation of China under Grants nos. 60736009 and 60901066.
Author information
Authors and Affiliations
Corresponding authors
Appendix
Appendix
Proof of Theorem 1

According to the formula of Cumulant-Moment (C-M), we have

In the following, it is proved that the fourth-order time-average moment spectrum of the second term (denoted as  ) is zero:
) is zero:

(Leonov-Shiryaev [14]):

(Triangle Inequality):

(Schwarz Inequality):

So

 is unequal to zero if and only if
is unequal to zero if and only if



We analyze four cases as follows.
-
(1)
None of the four frequency pairs satisfying (A.9) and (A.10) are unequal to
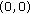 . According to (AS1), it is impossible.
. According to (AS1), it is impossible. -
(2)
Only one of the four frequency pairs satisfying (A.9) and (A.10) is zero. According to (AS1), it is impossible.
-
(3)
Two of the four frequency pairs satisfying (A.9) and (A.10) are equal to
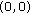 . Since
. Since 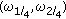 is not (0, 0) according to (AS1), there must be two pairs equal to
is not (0, 0) according to (AS1), there must be two pairs equal to  among
among 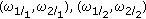 , and
, and  .
.Thus, the fourth-order time-average moment spectrum is
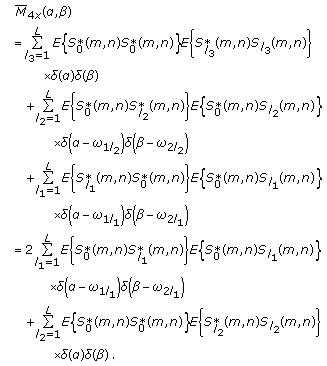 (A11)
(A11) -
(4)
All of the four frequency pairs satisfying (A.9) and (A.10) are unequal to
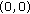 . Thus, the fourth-order time-average moment spectrum is
. Thus, the fourth-order time-average moment spectrum is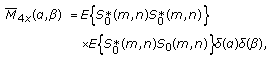 (A12)
(A12)
thus yielding

Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wu, SY., Liao, GS. & Yang, ZW. Two-Dimensional Harmonic Retrieval in Correlative Noise Based on Genetic Algorithm. EURASIP J. Adv. Signal Process. 2010, 569371 (2010). https://doi.org/10.1155/2010/569371
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/569371
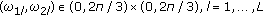 , frequency pairs are mutually unequal and not coupled;
, frequency pairs are mutually unequal and not coupled; s are deterministic constants in
s are deterministic constants in 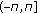 ;
;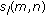 s and
s and 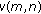 are mutually correlative and stationary stochastic processes with the mean
are mutually correlative and stationary stochastic processes with the mean  and
and 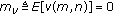 ;
;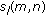 s and
s and 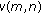 satisfy the so-called cross-mixing condition [
satisfy the so-called cross-mixing condition [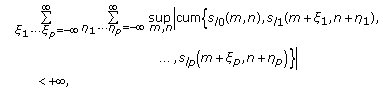
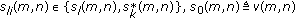 ,
, 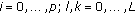 .
. . Create an initial population which includes
. Create an initial population which includes 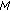 individuals and evaluate their fitness.
individuals and evaluate their fitness.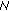 individuals.
individuals.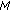 individuals from step 3 and
individuals from step 3 and 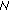 memorial individuals from step 2. Evaluate the distanced between each two of them. Introduce a penalty
memorial individuals from step 2. Evaluate the distanced between each two of them. Introduce a penalty 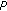 to the individual with lower fitness when
to the individual with lower fitness when 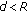 .
.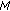 individuals with the
individuals with the  individuals. Sort the
individuals. Sort the  individuals according to their fitness. Save the first
individuals according to their fitness. Save the first 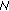 individuals and the first
individuals and the first 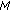 individuals.
individuals.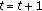 and repeat steps 3–6 until
and repeat steps 3–6 until 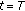 .
.
 of (7),
of (7),  is white Gaussian noise, SNR = 0 dB. 3D viewVertical viewEstimation based on GA
is white Gaussian noise, SNR = 0 dB. 3D viewVertical viewEstimation based on GA
 is white Gaussian noise, the data size is
is white Gaussian noise, the data size is
 .
.

 is white Gaussian noise, SNR = 0 dB.
is white Gaussian noise, SNR = 0 dB.

 of (7),
of (7),  is i. i.d white exponential noise, SNR = 0 dB.3D viewVertical viewEstimation based on GA
is i. i.d white exponential noise, SNR = 0 dB.3D viewVertical viewEstimation based on GA
 is i. i.d white exponential noise, the data size is
is i. i.d white exponential noise, the data size is  .
.
 is i. i.d white exponential noise, SNR = 0 dB.
is i. i.d white exponential noise, SNR = 0 dB.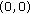 . According to (AS1), it is impossible.
. According to (AS1), it is impossible.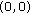 . Since
. Since 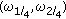 is not (0, 0) according to (AS1), there must be two pairs equal to
is not (0, 0) according to (AS1), there must be two pairs equal to  among
among 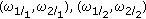 , and
, and  .
.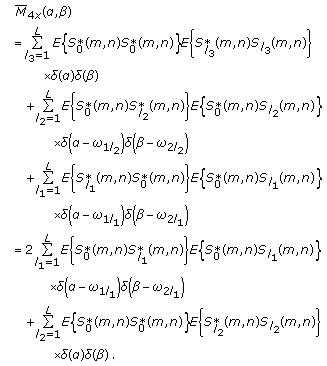
 . Thus, the fourth-order time-average moment spectrum is
. Thus, the fourth-order time-average moment spectrum is