- Research Article
- Open access
- Published:
Covariance Tracking via Geometric Particle Filtering
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 583918 (2010)
Abstract
Region covariance descriptor recently proposed has been approved robust and elegant to describe a region of interest, which has been applied to visual tracking. We develop a geometric method for visual tracking, in which region covariance is used to model objects appearance; then tracking is led by implementing the particle filter with the constraint that the system state lies in a low dimensional manifold: affine Lie group. The sequential Bayesian updating consists of drawing state samples while moving on the manifold geodesics; the region covariance is updated using a novel approach in a Riemannian space. Our main contribution is developing a general particle filtering-based racking algorithm that explicitly take the geometry of affine Lie groups into consideration in deriving the state equation on Lie groups. Theoretic analysis and experimental evaluations demonstrate the promise and effectiveness of the proposed tracking method.
1. Introduction
Visual tracking in an image sequence, which is now an active area of research in computer vision, is widely applied to vision guidance, surveillance, robotic navigation, human-computer interaction, and so forth. Dynamic deformation of object is a distinct problem in image-based tracking.
Conventional correlation-based trackers [1, 2] use either a region's gray information or edges and other features as the target signatures, but it is difficult to solve the problem of object region deformation in the tracking. Over the last 10 years, numerous approaches [3–10] have been proposed to address this problem. The main idea of them is molding geometric parameter models for the image motions of points within a target region. The parameter models including affine model, projective model, or other nonlinear models. The classic Lucas-Kanade tracker [3, 4] and Meanshift tracker [5] get the model parameters through gradient descent which minimizes the difference between the template and the current region of the image. These methods are computationally efficient. However, the methods may converge to a local maximum, they are sensitive to background clutter, occlusion, and quick moving objects. These problems can be mitigated by stochastic methods which maintain multiple hypotheses in the state space and in this way, achieve more robustness to the local maximum. Among various stochastic methods, particle filters [5–10] are very successful. Particle filters provide a robust tracking framework as they are neither limited to linear systems nor require the noise to be Gaussian. Particle filters simultaneously track multiple hypotheses and recursively approximate the posterior probability density function in the state space with a set of random sampled particles.
Many papers, such as [5–10] utilize particle filter method to track deformable target. They use affine transform as parameter model, and the six affine parameters were treated as a vector. However, the affine parameters belong to spaces which are not vector spaces, but instead a curved Lie group. In general, the system state of the particle filter lies in a constrained subspace whose dimension is much lower than the whole space dimension. Only a few recent papers have tried to use the geometry of the manifold to design Bayesian filtering algorithms [11, 12]. However, there is little discussion in the literature using the intrinsic geometry of manifold to develop particle filter-based tracking algorithms.
Object representation is one of major components for a typical visual tracker. Extensive researches have been done on this topic. Recently Tuzel et al. [13, 14] proposed an elegant and simple solution to integrate multiple features. In this method, covariance matrix was employed to represent the target. Using a covariance matrix to represent the target (region covariance descriptor) has many advantages: ( ) it embodies both spatial and statistical properties of the objects; (
) it embodies both spatial and statistical properties of the objects; ( ) it provides an elegant solution to fuse multiple features and modalities; (
) it provides an elegant solution to fuse multiple features and modalities; ( ) it has a very low-dimensionality; (
) it has a very low-dimensionality; ( ) it is capable of comparing regions without being restricted to a constant window size; and (
) it is capable of comparing regions without being restricted to a constant window size; and ( ) the estimation of the covariance matrix can be easily implemented.
) the estimation of the covariance matrix can be easily implemented.
In this paper, we integrate covariance descriptor into Mont Carlo technique for visual tracking, study the geometry structure of affine Lie groups, and propose a tracking algorithm through particle filtering on manifolds, which implement the particle filter with the constraint that the system state lies in a low dimensional manifold, The sequential Bayesian updating consists drawing state samples while moving on the manifold geodesics; this provides a smooth prior for the state space change. The regions covariance matrices are updated using a novel approach in a Riemannian space. Theoretic analysis and experimental results shows the promise and effectiveness of the approach proposed.
The paper is organized as follows. In Section 2, The mathematical background is described. Section 3 shows the object regions descriptor and the new update solution for those descriptors. Section 4 describes the tracking algorithm using geometric particle filtering. Results on real image sequences for evaluating algorithm performance are discussed in Section 5.Section 6 concludes this paper.
2. Manifold and Lie Group
The tools used here come primarily from differential geometry. For more information on these subjects, the reader is referred to [15, 16].
A manifold is a topological space that is locally similar to an Euclidean space. Intuitively, we can think of a manifold as a continuous surface lying in a higher dimensional Euclidean space. Analytic manifolds satisfy some further conditions of smoothness [16]. From now onwards, we restrict ourselves to analytic manifolds and by manifold we mean analytic manifold.
The tangent space,  at
at  , is the plane tangent to the surface of the manifold at that point. The tangent space can be thought of as the set of allowable velocities for a point constrained to move on the manifold. For
, is the plane tangent to the surface of the manifold at that point. The tangent space can be thought of as the set of allowable velocities for a point constrained to move on the manifold. For  -dimensional manifolds, the tangent space is a
-dimensional manifolds, the tangent space is a  -dimensional vector space. An example of a two-dimensional manifold embedded in
-dimensional vector space. An example of a two-dimensional manifold embedded in  with the tangent space
with the tangent space  is shown in Figure 1. The solid arrow
is shown in Figure 1. The solid arrow  is a tangent at
is a tangent at  . The distance between two points on the manifold is given in terms of the lengths of curves between them. The length of any curve is defined by an integral over norms of tangents [17]. The curve with minimum length is known as the geodesic and the length of the geodesic is the intrinsic distance. Parameter spaces occurring in computer vision problems usually have well-studied geometries and closed form formulae for the intrinsic distance are available. Tangents and geodesics are closely related. For each tangent
. The distance between two points on the manifold is given in terms of the lengths of curves between them. The length of any curve is defined by an integral over norms of tangents [17]. The curve with minimum length is known as the geodesic and the length of the geodesic is the intrinsic distance. Parameter spaces occurring in computer vision problems usually have well-studied geometries and closed form formulae for the intrinsic distance are available. Tangents and geodesics are closely related. For each tangent  , there is a unique geodesic starting at
, there is a unique geodesic starting at  with initial velocity
with initial velocity  . The exponential map,
. The exponential map,  maps
maps  to the point on the manifold reached by this geodesic.
to the point on the manifold reached by this geodesic.
A Lie group is a group with the structure of an analytic manifold such that the group operations are analytic, that is the maps

are analytic [15]. The local neighborhood of any group element  can be adequately described by its tangent-space. The tangent-space at the identity element forms its Lie algebra.
can be adequately described by its tangent-space. The tangent-space at the identity element forms its Lie algebra.
The set of nonsingular  square matrices forms a Lie group where the group product is modeled by matrix multiplication, usually denoted by
square matrices forms a Lie group where the group product is modeled by matrix multiplication, usually denoted by  for the general linear group of the order
for the general linear group of the order  . Lie groups are differentiable manifolds on which we can do calculus.
. Lie groups are differentiable manifolds on which we can do calculus.
In our task, we use affine transformation as parameter model. The set of all affine transformation forms a matrix Lie group.
3. Region Covariance Descriptor
Let  be the observed image with size of
be the observed image with size of  , and
, and  be
be  dimensional feature image extracted from
dimensional feature image extracted from 

where  can be any mapping such as color, gradients, filter responses, and so forth. Let
can be any mapping such as color, gradients, filter responses, and so forth. Let  be the
be the  -dimensional feature points inside a given rectangular region. The region is represented by the
-dimensional feature points inside a given rectangular region. The region is represented by the  covariance matrix of the feature points
covariance matrix of the feature points

where  is the number of pixels in the region.
is the number of pixels in the region.  is the mean of the feature points.
is the mean of the feature points.
In our task, we define  as
as

where  and
and  are the pixel location in
are the pixel location in  ;
;  is the gray value;
is the gray value;  and
and  are first derivatives of
are first derivatives of  ; In this way, the region
; In this way, the region  is mapped into a
is mapped into a  covariance matrix.
covariance matrix.
In a tracking process, the objects appearance changes over time. This dynamic behavior requires a robust temporal update of the region covariance descriptors and the definition of dissimilarity metric for the region covariance. The important question here is how to measure the dissimilarity between two region covariance matrices and how to update the regions covariance matrix in the next time slot. Note that the covariance matrices do not lie on Euclidean space. For example, the space is not closed under multiplication with negative scalars. So, it is necessary to get the dissimilarity between two covariance matrices in a different space. To overcome this problem a Riemannian Manifold is used.
3.1. Dissimilarity Metric
The dissimilarity between two regions covariance matrices can be given by the distance between two points of the manifold  , considering that those points are the two regions.
, considering that those points are the two regions.
The covariance matrix, which is symmetric positive definite matrix, forms a Riemannian manifold. According to [14], we define a Riemannian metric like that

The exponential map associated to the above Riemannian metric is

By (6), we can obtain the logarithm map

Submit (7) to (5)

Furthermore, (8) is equivalent to

where  are the generalized eigenvalues of
are the generalized eigenvalues of  and
and  .
.
3.2. Covariance Update
A solution for the covariance matrices update was proposed in [14], that is based on the estimation of the points mean on a Riemannian Manifold, where each point corresponds to a covariance matrix. This mean estimation is obtained using a gradient descent approach. In this paper, we propose a novel solution for the covariance matrix update, that is based on the mean of the new covariance matrix and the last covariance updated. If  is the velocity that takes us from
is the velocity that takes us from  to
to  ,
,  will be the half distance to point
will be the half distance to point  . Using (6) and (7), we have
. Using (6) and (7), we have

where  is the average distance between two points on a Riemannian Manifold (the updated covariance matrix). This update means that the present covariance is more important than the previous covariances. Since we are tracking objects that can change over time, the last information about them is more reliable.
is the average distance between two points on a Riemannian Manifold (the updated covariance matrix). This update means that the present covariance is more important than the previous covariances. Since we are tracking objects that can change over time, the last information about them is more reliable.
4. Tracking Model
The visual tracking problem is cast as an inference task in a Markov model with hidden state variables. The state variable  describes the affine parameters of the target at time
describes the affine parameters of the target at time  . Given a set of observed images
. Given a set of observed images  , we aim to estimate the value of the hidden state variable
, we aim to estimate the value of the hidden state variable  . Using Bayesian theorem, we have the familiar result
. Using Bayesian theorem, we have the familiar result


Equation (11) is called the prediction equation and (12) is called the update equation. The tracking process is governed by the observation model  , where we estimate the likelihood of
, where we estimate the likelihood of  observing
observing  , and the dynamical model between two states
, and the dynamical model between two states  .
.
4.1. Dynamical Model
Dynamical model, also known as state transition model, can describe transition of object state in tracking process. In visual tracking problems, it is ideal to have an exact state transition model. In practice, however approximations models are used. The deformation and location of a target object in an image can be represented by affine transform. In this work, the state at time  consists of the six parameters of an affine transformation. 2-D affine transformation of the image can be written as
consists of the six parameters of an affine transformation. 2-D affine transformation of the image can be written as

where  and
and  denote the location of the corresponding points between two images,
denote the location of the corresponding points between two images,  is a
is a  nonsingular matrix and translation vector
nonsingular matrix and translation vector  ,
,  denotes affine transformation parameters. The transformation can be expressed in homogeneous coordinates as
denotes affine transformation parameters. The transformation can be expressed in homogeneous coordinates as

 specify the displacement between
specify the displacement between  and
and  , we define
, we define  as velocities between
as velocities between  and
and  , which specify the motion. These defines are analogous to the vector space case in that the velocities are determined by the tangent vectors along geodesics connecting the observed points (
, which specify the motion. These defines are analogous to the vector space case in that the velocities are determined by the tangent vectors along geodesics connecting the observed points ( . Then the state transition model is of the following form:
. Then the state transition model is of the following form:


where  is a discrete-time trajectory on a six-dimensional affine Lie group,
is a discrete-time trajectory on a six-dimensional affine Lie group,  is a velocity on the corresponding Lie algebra,
is a velocity on the corresponding Lie algebra,  are Gaussian white zero-mean stochastic processes.
are Gaussian white zero-mean stochastic processes.
The tracking algorithm will not require the explicit functional form of the prior density; it will be dependent on the samples generated from the prior density. In a Markovian time-series analysis, often there is a standard characterization of a time-varying posterior density, in a convenient recursive form. This characterization relates an underlying Markov process to its observations at each observation time via a pair of state transition equations. The following algorithm specifies a procedure to sample from the conditional prior  :
:
Algorithm 1.
For some  , we are given the values for
, we are given the values for  and
and  . For
. For  :
:
-
(1)
Generate a sample of
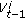 , given
, given 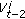 , according to (16).
, according to (16). -
(2)
For each sample of
 , calculate
, calculate 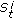 according to
according to 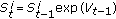 .
.
The Algorithm 1 consists in drawing state samples while moving on the manifold geodesics. This geodesics sample give a dynamics-based smoothing prior on the state transition space. Figure 2 is an illustration of this geodesics sample process.
4.2. Observation Model
Next, we specify the probability model for the observed images.  is the likelihood through the observation
is the likelihood through the observation  under the state
under the state 

where  be covariance features of the template image, and
be covariance features of the template image, and  denote covariance features at the transformation
denote covariance features at the transformation  .
.
4.3. Sequential Monte Carlo Approach
The Monte Carlo idea is to approximate the posterior density of  by a large number of samples drawn from it. Having obtained the samples, any estimate of
by a large number of samples drawn from it. Having obtained the samples, any estimate of  (MMSE, MAP, etc.) can be approximated using sample averages.
(MMSE, MAP, etc.) can be approximated using sample averages.
A recursive formulation, which takes samples from  and generates the samples from
and generates the samples from  in an efficient fashion, is desirable. We accomplish this task using ideas from sequential methods and importance sampling. Assume that, at the observation time
in an efficient fashion, is desirable. We accomplish this task using ideas from sequential methods and importance sampling. Assume that, at the observation time  , we have a set of
, we have a set of  samples from the posterior,
samples from the posterior,  . Following are the steps to generate the set
. Following are the steps to generate the set  .
.
Prediction
The first step is to sample from  given the samples from
given the samples from  . According to (11),
. According to (11),  is the integral of the product of a marginal and a conditional density. This implies that, for each element
is the integral of the product of a marginal and a conditional density. This implies that, for each element  , by generating a sample from the conditional,
, by generating a sample from the conditional,  we can generate a sample from
we can generate a sample from  . In our case, this is accomplished using Algorithm 1. Now we have samples
. In our case, this is accomplished using Algorithm 1. Now we have samples  from
from  ; these samples are called predictions, but we have used a geodesics prediction different to classic particle filter on vector space.
; these samples are called predictions, but we have used a geodesics prediction different to classic particle filter on vector space.
Resampling
Given these predictions, the next step is to generate samples from the posterior  . For this, we utilize importance sampling as follows. The samples from the prior
. For this, we utilize importance sampling as follows. The samples from the prior  are resampled according to the probabilities that are proportional to the likelihoods
are resampled according to the probabilities that are proportional to the likelihoods  . Form a discrete probability mass function on the set
. Form a discrete probability mass function on the set 

Then, resample  values from the set
values from the set  according to probability
according to probability  . These values are desired samples from the posterior
. These values are desired samples from the posterior  . Denote the resampled set by
. Denote the resampled set by  ,
,  .
.
Averaging on the Lie Group
Now that we have  samples from the posterior
samples from the posterior  , we can average them appropriately to approximate the posterior mean of
, we can average them appropriately to approximate the posterior mean of  .
.
It may be recalled that for a vector space, the sample mean or average of a set  is given by
is given by  . However, such a notion cannot be applied directly to elements of a group manifold. There are at least two ways of define a mean value on a manifold: extrinsic means and intrinsic means. The extrinsic mean depends on the geometry of the ambient space and the embedding. The intrinsic mean is defined using only the intrinsic geometry of the manifold. In general, the intrinsic average is preferable over the extrinsic average but is often hard to compute due to the nonlinearity of the Riemannian distance function and the need to parameterize the group manifold. However, as we will see here, for matrix Lie groups the intrinsic average can be computed efficiently. In several applications, the Lie algebra is used for computing intrinsic means of points having Lie group structure [17–19]. We adopt the similar idea to obtain the intrinsic mean of the affine lie group.
. However, such a notion cannot be applied directly to elements of a group manifold. There are at least two ways of define a mean value on a manifold: extrinsic means and intrinsic means. The extrinsic mean depends on the geometry of the ambient space and the embedding. The intrinsic mean is defined using only the intrinsic geometry of the manifold. In general, the intrinsic average is preferable over the extrinsic average but is often hard to compute due to the nonlinearity of the Riemannian distance function and the need to parameterize the group manifold. However, as we will see here, for matrix Lie groups the intrinsic average can be computed efficiently. In several applications, the Lie algebra is used for computing intrinsic means of points having Lie group structure [17–19]. We adopt the similar idea to obtain the intrinsic mean of the affine lie group.
The "true" intrinsic sample mean is given by

It will be recalled that for matrix groups, the Riemannian distance is defined by the matrix logarithm operation, that is for matrix group elements  and
and  we have
we have

4.4. Detail of Tracking Algorithm
Algorithm 2.
 Initialize:
Initialize:
Generate samples  from the prior distribution
from the prior distribution  . Set initial weights
. Set initial weights  .
.
 Prediction:
Prediction:
Draw  from the conditional prior according to Algorithm1.
from the conditional prior according to Algorithm1.
 Importance Weights:
Importance Weights:
Compute the probability  according to (18).
according to (18).
 Resampling:
Resampling:
Generate  samples from the set
samples from the set  with the associated probabilities
with the associated probabilities  . Denote these samples by
. Denote these samples by  .
.
 MMSE Averaging:
MMSE Averaging:
Calculate the sample average according to (19) which is the target state. Set  and go to step
and go to step  .
.
5. Experimental Results
In order to evaluate the performance of the proposed tracking algorithm based on geometric particle filtering and the new update method. We start by comparing proposed algorithm (referred as  ) with the tracking algorithm based on Particle filtering on vector space (
) with the tracking algorithm based on Particle filtering on vector space ( ) [5–10] with the same real image sequences. After that, we evaluated the proposed update method with the one previously proposed in the literature. We also tested the proposed algorithm under varying illumination conditions. These algorithms are implemented in C++ running on an Intel Core-2 2.5 GHz processor with 2 GB memory.
) [5–10] with the same real image sequences. After that, we evaluated the proposed update method with the one previously proposed in the literature. We also tested the proposed algorithm under varying illumination conditions. These algorithms are implemented in C++ running on an Intel Core-2 2.5 GHz processor with 2 GB memory.
5.1. Compared with VPF
Two typical image sequences where the objects undergo large changes in pose and scale were tested using  and VPF. Thus, the performance of the two algorithms has been compare with the same experimental setup.
and VPF. Thus, the performance of the two algorithms has been compare with the same experimental setup.
The first sequence contains 150 frames of images, the size of each frame is  and the size of template is
and the size of template is  . The target to track undergo large scale change in the sequence. For the particle filtering in the visual tracking, the number of particles is set to 60. The Standard Deviations of the six affine parameters in 16 are assigned as
. The target to track undergo large scale change in the sequence. For the particle filtering in the visual tracking, the number of particles is set to 60. The Standard Deviations of the six affine parameters in 16 are assigned as  . The final tracking results of
. The final tracking results of  and VPF are shown in Figure 3. For a better visualization, we just show the tracking results of four representative frames 52, 87, 135 and 148. The frame number is shown on the top left corner of each image. The value below each image is the likelihood of the matching, the smaller the matching error, the larger the likelihood. Figure 4(a) shows the likelihood curves.
and VPF are shown in Figure 3. For a better visualization, we just show the tracking results of four representative frames 52, 87, 135 and 148. The frame number is shown on the top left corner of each image. The value below each image is the likelihood of the matching, the smaller the matching error, the larger the likelihood. Figure 4(a) shows the likelihood curves.
From Figure 3, we see that the proposed tracking algorithm exhibits a robust tracking result and the tracking window adapt with the scale change of the target. While  tracker begin to drift away form the target form frame 135. This due to the fact that the
tracker begin to drift away form the target form frame 135. This due to the fact that the  treats the parameter space as a whole. There is not enough observations to provide a reliable estimate. While
treats the parameter space as a whole. There is not enough observations to provide a reliable estimate. While  consider the geometry of the parameter space, this prior of smooth changes of the parameter space. From Figure 4(a), we see that likelihoods of
consider the geometry of the parameter space, this prior of smooth changes of the parameter space. From Figure 4(a), we see that likelihoods of  tracker are always larger than
tracker are always larger than  tracker. The second sequence contains 370 frames of images, the size of each frame is
tracker. The second sequence contains 370 frames of images, the size of each frame is  and the size of template is
and the size of template is  . The target to track experiences large rotation change and shear change in the sequence. The number of particles is set to 60. The Standard Deviation of the six affine parameters in (16) are assigned as
. The target to track experiences large rotation change and shear change in the sequence. The number of particles is set to 60. The Standard Deviation of the six affine parameters in (16) are assigned as  . The final tracking results of
. The final tracking results of  and
and  are shown in Figure 5. Like sequence 1, we just show the tracking results of four representative frames 165, 281, 337 and 364. We see that the proposed tracking algorithm exhibits a robust tracking result and the tracking window adapt with the deformation of the target. While the tracking window of
are shown in Figure 5. Like sequence 1, we just show the tracking results of four representative frames 165, 281, 337 and 364. We see that the proposed tracking algorithm exhibits a robust tracking result and the tracking window adapt with the deformation of the target. While the tracking window of  can not enclose the target well. So, the likelihoods are smaller than
can not enclose the target well. So, the likelihoods are smaller than  . Figure 4(b) shows the likelihood curves. we see that in the first 150 frames the likelihoods of the two tracker is similar, but from 150th frame the likelihood of
. Figure 4(b) shows the likelihood curves. we see that in the first 150 frames the likelihoods of the two tracker is similar, but from 150th frame the likelihood of  is always larger than
is always larger than  . This is due to the fact that the target does not experience rotation and shear changes before 150th frame, just translation.
. This is due to the fact that the target does not experience rotation and shear changes before 150th frame, just translation.
In summary, we observe that the  tracker outperforms
tracker outperforms  in the scenarios of scale, rotation, and shear changes of target.
in the scenarios of scale, rotation, and shear changes of target.
5.2. Update Method
To evaluate the effectiveness of the proposed update solution, we compare the result of it with the ones obtained by the Porikli update proposed in [14]. We compare the likelihood curves between above two image sequences; the results were obtained by just changing the update method.
Figure 6 shows the likelihood curves of the two update methods. From Figure 6, we see that likelihoods curves are similar; this means the two updates are equivalent.
However, the distinct advantage of this new update method is the time execution. In Table 1, we show the results in milliseconds of the two updates methods. The Porikli update time execution was measured considering a stack of five regions covariance matrices. The new update is much faster than the one proposed in [14], with an average performance of 0.6 ms.
5.3. Illumination Changes
To analyze the robustness against the illumination changes using the covariance descriptor, we have used the algorithm on several sequences with illumination changes. One of which is a vehicle driving at night, shown in Figure 7(a). Despite the difficult illumination conditions, our algorithm is able to track the vehicle well. We also test the same image sequence using the image grayscale values. Tracking results are shown in Figure 7(b). we can see that from 280th frame, the tracking window drift away from the target, the red dashed window is the real target. So the tracking algorithm using covariance descriptor outperformed gray-based tracking algorithm under illumination changes.
5.4. Experimental Analyses
The algorithm described in the paper consists of three components.
-
(1)
We develop a general particle filtering based tracking algorithm that explicitly take the geometry of affine Lie groups into consideration in deriving the state equation on Lie groups. This one is our main contribution and the dominating factor in improving the tracking performance.
-
(2)
We use region covariance descriptor to model objects appearance, the edge-like information more robust to the illumination changes than the image grayscale can be simultaneously considered with the image grayscale information and pixel spatial information, and the consequence is the quite robust tracking results as seen in Figure 7.
-
(3)
We updated region covariance using a novel approach in a Riemannian space. The new update method has improved the real-time performance.
So the order of importance to the performance among these components is 1, 2, 3.
6. Conclusion
In this paper, we have proposed a visual tracking method, which integrate covariance descriptor into Mont Carlo tracking technique for visual tracking. The distinct advantage of this new approach is carrying Sequential Monte Carlo method over the affine Lie group, which consider the geometry prior of the parameter space. Theoretic analysis and experimental results shows the promise and effectiveness of the approach proposed.
This paper highlights the role of Monte Carlo methods in statistical inferences over affine lie group for visual tracking problem. There are several directions for extending the new idea. One is to consider more general differentiable manifolds beyond the affine lie group. In addition, we can deepen and broaden this research to other image processing problems.
References
Montera DA, Rogers SK, Ruck DW, Oxley ME: Object tracking through adaptive correlation. Optical Engineering 1994, 33: 294-302. 10.1117/12.152013
Parry HS, Marshall AD, Markham KC: Tracking targets in FLIR images by region template correlation. Acquisition, Tracking, and Pointing XI, April 1997, Orlando, Fla, USA, Proceedings of SPIE 3086: 221-232.
Hager GD, Belhumeur PN: Efficient region tracking with parametric models of geometry and illumination. IEEE Transactions on Pattern Analysis and Machine Intelligence 1998, 20(10):1025-1039. 10.1109/34.722606
Baker S, Matthews I: Lucas-Kanade 20 years on: a unifying framework. International Journal of Computer Vision 2004, 56(3):221-255.
Zhang H, Huang W, Huang Z, Li L: Affine object tracking with kernel-based spatial-color representation. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '05), June 2005 293-300.
Isard M, Blake A: Condension-conditional density propagation for visual tracking. International Journal of Computer Vision 1998, 29(1):5-28. 10.1023/A:1008078328650
Zhou SK, Chellappa R, Moghaddam B: Visual tracking and recognition using appearance-adaptive models in particle filters. IEEE Transactions on Image Processing 2004, 13(11):1491-1506. 10.1109/TIP.2004.836152
Rathi Y, Vaswani N, Tannenbaum A, Yezzi A: Tracking deforming objects using particle filtering for geometric active contours. IEEE Transactions on Pattern Analysis and Machine Intelligence 2007, 29(8):1470-1475.
Odobez J-M, Gatica-Perez D, Ba SO: Embedding motion in model-based stochastic tracking. IEEE Transactions on Image Processing 2006, 15(11):3514-3530.
Ross DA, Lim J, Lin R-S, Yang M-H: Incremental learning for robust visual tracking. International Journal of Computer Vision 2008, 77(1–3):125-141.
Srivastava A, Klassen E: Monte Carlo extrinsic estimators of manifold-valued parameters. IEEE Transactions on Signal Processing 2002, 50(2):299-308. 10.1109/78.978385
Snoussi H, Mohammad-Djafari A: Particle filering on Riemannian manifold. Proceedings of the 27th International Workshop on Bayesian Inference and Maximum Entropy Methods in Science and Engineering, 2006, AIP Conference Proceedings 872: 219-226.
Tuzel O, Porikli F, Meer P: Region covariance: a fast descriptor for detection and classification. Proceedings of the 9th European Conference on Computer Vision (ECCV '06), 2006, Lecture Notes in Computer Science 3952: 589-600.
Porikli F, Tuzel O, Meer P: Covariance tracking using model update based on Lie algebra. Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '06), June 2006, New York, NY, USA 1: 728-735.
Hall BC: Lie Algebras, and Representations: An Elementary Introduction. Springer, New York, NY, USA; 2003.
Berger M: A Panoramic View of Riemannian Geometry. Springer, Berlin, Germany; 2003.
Begelfor E, Werman M: How to put probabilities on homographies. IEEE Transactions on Pattern Analysis and Machine Intelligence 2005, 27(10):1666-1670.
Govindu VM: Lie-algebraic averaging for globally consistent motion estimation. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR '04), July 2004, Washington, DC, USA 1: 684-691.
Tuzel O, Subbarao R, Meer P: Simultaneous multiple 3D motion estimation via mode finding on lie groups. Proceedings of the 10th IEEE International Conference on Computer Vision (ICCV '05), October 2005, Beijing, China 1: 18-25.
Acknowledgments
This work is partly supported by the National Natural Science Foundation of China (Grant no. 60603097) and the National Defense Innovation Foundation of Chinese Academy Sciences (CXJJ-65).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, Y., Li, G. & Shi, Z. Covariance Tracking via Geometric Particle Filtering. EURASIP J. Adv. Signal Process. 2010, 583918 (2010). https://doi.org/10.1155/2010/583918
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/583918

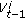 , given
, given 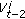 , according to (16).
, according to (16). , calculate
, calculate 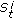 according to
according to 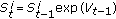 .
.




