- Research Article
- Open access
- Published:
Facial Affect Recognition Using Regularized Discriminant Analysis-Based Algorithms
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 596842 (2010)
Abstract
This paper presents a novel and effective method for facial expression recognition including happiness, disgust, fear, anger, sadness, surprise, and neutral state. The proposed method utilizes a regularized discriminant analysis-based boosting algorithm (RDAB) with effective Gabor features to recognize the facial expressions. Entropy criterion is applied to select the effective Gabor feature which is a subset of informative and nonredundant Gabor features. The proposed RDAB algorithm uses RDA as a learner in the boosting algorithm. The RDA combines strengths of linear discriminant analysis (LDA) and quadratic discriminant analysis (QDA). It solves the small sample size and ill-posed problems suffered from QDA and LDA through a regularization technique. Additionally, this study uses the particle swarm optimization (PSO) algorithm to estimate optimal parameters in RDA. Experiment results demonstrate that our approach can accurately and robustly recognize facial expressions.
1. Introduction
Human-computer interaction (HCI) technologies have attracted more and more attention. The traditional interface devices such as the keyboard and mouse are constructed to transmit explicit messages. The implicit information about the user, such as changes in the affective state, is ignored. However, HCI is moving gradually from computer-centered designs toward human-centered designs [1, 2]. Designs for human-centered computing should focus on the human portion of the HCI context, like nonlinguistic conversational signal, emotion, and affective states. Human-centered interfaces must have the ability to detect human affective behavior because it conveys fundamental components of human-human communication. These affective states motivate human actions and enrich the meaning of human communication.
Previous research [3] shows that 55% of face-to-face human communication is relied on facial expressions, indicating that facial expressions play an important role in social interactions between human beings. As a result, facial expressions are also an important part of HCI. Thus, automatic facial expression recognition in the human-computer environment is an essential and challenging task.
Various techniques have been developed for automatic facial expression recognition. Three recent surveys [4–7] on this topic indicate that facial expression recognition has grown more sophisticated. Facial expression recognition techniques can be categorized based on recognition targets or data sources. With respect to recognition targets, most techniques attempt to recognize a small set of prototypic emotional expressions, that is, happiness, surprise, anger, sadness, fear, and disgust, as well as the neutral state. This practice is based on the work of Darwin [8] and more recently Keltner and Ekman [9] who proposed that basic emotions have corresponding prototypic facial expressions. Ekman and Friesen [10] developed the Facial Action Coding System (FACS) for describing facial expressions in terms of action units (AUs). FACS consists of 46 AUs, which describe basic facial movements based on muscle activities. Various researchers engage in AUs recognition to model facial actions [11].
Facial expression recognition techniques can generally be divided into two categories based on their data sources: static images and image sequences. In sequence-based methods, an image sequence displays one expression. Thus, a neutral face must be identified first to serve as a baseline face. Then, expression recognition depends on the difference between the baseline face and the following input face image. Optical flow estimation is a typical method of extracting facial features. Yacoob and Davis [12] used the optical flow approach to track the motion of facial features from image sequences and classified the extracted facial features into six basic expressions. Bartlett et al. [13] used a method combining principal component analysis (PCA) with optical flow for facial expression recognition. Essa and Pentland [14] used optical flow in a physical model of the face with a recursive framework to classify facial expressions. Xiang et al. [15] used Fourier transform to extract facial features and represent expressions. These features are then processed using fuzzy C means clustering to generate a spatiotemporal model for each expression type.
If the baseline image in the sequence-based methods is not identified correctly, it is difficult to identify the facial expression for a given image frame. However, facial expression recognition using static images is more difficult than that using image sequences because less information is available. Psychologists often use single images for expression recognition. Therefore, facial expression recognition using static images has attracted a lot of attention. Chen and Huang [16] proposed a clustering-based feature extraction method for facial expression recognition. They used the AR database, created by Aleix Martinez and Robert Benavente, to classify three facial expressions: neutral, smiling, and angry. Zhi and Ruan [17] proposed a method called the two-dimensional discriminant locality preserving projections (2D-DLPPs) algorithm and applied the method to facial expression recognition in a Japanese female facial expression database (JAFFE) and the Cohn-Kanade database. Shin et al. [18] combined the two-dimensional learning discriminant analysis (2D-LDA) and support vector machine (SVM) methods to recognize seven basic expressions. Feng et al. [19] divided face images into small regions and extracted local binary pattern (LBP) histograms as features and then used a linear programming technique to classify seven facial expressions.
This paper proposes a novel regularized discriminant analysis-based boosting algorithm (RDAB) to recognize seven expressions, including happiness, surprise, anger, sadness, fear, disgust, and a neutral state, from static images. The proposed method also employs an entropy criterion to select effective Gabor features for facial image representation which is a subset of informative and non-redundant Gabor features. In RDAB, regularized discriminant analysis (RDA) acts as a learner in the boosting algorithm. RDA combines the strengths of linear discriminant analysis (LDA) and quadratic discriminant analysis (QDA) and solves the small sample size and ill-posed problems of QDA and LDA by regularizing parameters. This study also uses a particle swarm optimization (PSO) algorithm to estimate the optimal parameters in RDA. Experiment results demonstrate that the proposed RDAB facial expression method achieves a high recognition rate and outperforms other facial expression recognition systems.
The rest of this paper is organized as follows. Section 2 provides an overview of the proposed method. Section 3 describes each component of the proposed method. Section 4 presents experiment results. Finally, conclusions are summarized in Section 5.
2. Overview of the Proposed Method
The overall process of the proposed facial expression recognition method is displayed in Figure 1. First, the preprocessing step is applied to input images to produce standardized facial images for subsequent processing. Facial images are detected using the Viola and Jones face detector [20]. The original images are cropped into face images and resized to  . Then, a histogram equalization method is applied to eliminate variations in illumination. Several previous studies [21] show that classification using downsampled images in pattern recognition produces a higher accuracy than using the original images. Using downsampled images also reduces the computation complexity. Thus, the following feature extraction step uses facial images that have been downsampled by a factor of two.
. Then, a histogram equalization method is applied to eliminate variations in illumination. Several previous studies [21] show that classification using downsampled images in pattern recognition produces a higher accuracy than using the original images. Using downsampled images also reduces the computation complexity. Thus, the following feature extraction step uses facial images that have been downsampled by a factor of two.
Automated facial expression recognition must solve two basic problems: facial feature extraction and facial expression classification. Facial feature extraction methods can be categorized in terms of image sequences or static images. Motion extraction approaches directly focus on facial changes that occur due to facial expressions, whereas static image-based methods do not rely on neutral face images to extract facial features. Gabor features are widely used in image analysis because they closely model the receptive field properties of cells in the primary visual cortex [22–24]. Therefore, this study uses Gabor features to recognize facial expressions from static images.
In practice, the dimensionality of a Gabor feature vector is so high that the computation and memory requirements are very large. For example, if an image measures  pixels, the dimensionality of the Gabor feature vector with three frequencies and eight orientations is 294912 (
pixels, the dimensionality of the Gabor feature vector with three frequencies and eight orientations is 294912 ( ). Some of these features are similar. In other words, using the Gabor features with all frequencies and orientations is redundant. For this reason, several sampling methods have been proposed to determine the "optimal" subset for extracting Gabor features. Liu et al. [25] proposed an optimal sampling of Gabor features using PCA for face recognition. Additionally, AdaBoost has been widely used for feature selection [26–28]. This study proposes an effective Gabor feature selection to extract the informative Gabor features representing the facial characteristics. Entropy is used as a criterion to measure the importance of the feature. This approach reduces the feature dimensionality without losing much information and also decreases computation and storage requirements.
). Some of these features are similar. In other words, using the Gabor features with all frequencies and orientations is redundant. For this reason, several sampling methods have been proposed to determine the "optimal" subset for extracting Gabor features. Liu et al. [25] proposed an optimal sampling of Gabor features using PCA for face recognition. Additionally, AdaBoost has been widely used for feature selection [26–28]. This study proposes an effective Gabor feature selection to extract the informative Gabor features representing the facial characteristics. Entropy is used as a criterion to measure the importance of the feature. This approach reduces the feature dimensionality without losing much information and also decreases computation and storage requirements.
In the facial expression classification step, several classifiers have been proposed to cope with the facial expression classification problem, including neural networks, support vector machines (SVMs), and boosting algorithms. SVMs and boosting algorithms are both large margin classifiers primarily designed for two-class classification problems. SVMs often adopt one-against-one strategy or one-against-all procedure to deal with multiclass problems. On the other hand, boosting algorithms can solve multiclass problems using a multiclass learner. Thus, several researchers have used boosting algorithms with different learners to process multiclass problems. Yang et al.[29] adopted the AdaBoost algorithm to learn the combination of optimal discriminative features to construct the classifier and classify seven expressions and several AUs. Lu et al.[30] developed a novel boosting algorithm combined with LDA-based learners for face recognition. This paper proposes an RDA-based boosting algorithm to recognize facial expressions. RDA combines the benefits of LDA and QDA to achieve a higher recognition rate.
3. Automatic Facial Expression Recognition System
The block diagram of the automatic facial expression recognition system is shown in Figure 1. The key components of the proposed approach include ( ) preprocessing, (
) preprocessing, ( ) effective Gabor feature selection, and (
) effective Gabor feature selection, and ( ) RDAB classification. The details of proposed method are described as follows.
) RDAB classification. The details of proposed method are described as follows.
3.1. Preprocessing
This preprocessing is an important step because the input images usually have some slight differences, such as head tilt and head size. The preprocessing phase takes the segmented face, normalizes the face images, reduce lighting variations, and downsamples the face images. The preprocessing phase contains the following steps.
-
(1)
It detects faces from input images.
-
(2)
It normalizes the face regions with respect to a 128 × 96 face image by using the eyes and nose as reference points.
-
(3)
It performs histogram equalization to reduce the nonuniformity in the pixel distributions that may occur due to various imaging situations.
-
(4)
It downsamples the face images to obtain the low-frequency images. In this way, the noise and the computation complexity will be reduced.
3.2. Effective Gabor Feature Extraction
The Gabor filter is a very useful tool in computer vision and image analysis because it has optimal localization properties in both spatial and frequency analysis. A 2D Gabor filter is a complex field sinusoidal grating modulated by a 2D Gaussian function in the spatial domain. The 2D Gabor filter  is defined as
is defined as

where  are rotated coordinates, in which the major axis is oriented at an angle
are rotated coordinates, in which the major axis is oriented at an angle  from the x-axis,
from the x-axis,  represents a particular 2D frequency, and
represents a particular 2D frequency, and

where  and
and  represent the spatial extent and bandwidth of the filter, and
represent the spatial extent and bandwidth of the filter, and  is the aspect ratio between x and y axes. For convenience, we assume that
is the aspect ratio between x and y axes. For convenience, we assume that  , the aspect ratio is
, the aspect ratio is  , and the x-axis of the Gaussian has the same orientation as the frequency; hence, (1) can be simplified to
, and the x-axis of the Gaussian has the same orientation as the frequency; hence, (1) can be simplified to

where  is called the modulation frequency.
is called the modulation frequency.
This study considers a class of self-similar functions called Gabor wavelets. Using (3) as the mother Gabor wavelet, the self-similar filter bank can be derived by dilations and rotations of  through the generating function:
through the generating function:

where  ,
,  , and
, and  . The subscripts m and n represent the index for scale (dilation) and orientation (rotation). S is the total number of scales and T is the total number of orientations.
. The subscripts m and n represent the index for scale (dilation) and orientation (rotation). S is the total number of scales and T is the total number of orientations.
For a given input image  , the magnitude of a filtered image
, the magnitude of a filtered image  can be obtained as
can be obtained as

where  indicates 2-D convolution, and
indicates 2-D convolution, and  and
and  represent the real and imaginary parts of the Gabor filters from (4). The real part of Gabor filters with three scales and eight orientations is shown in Figure 2.
represent the real and imaginary parts of the Gabor filters from (4). The real part of Gabor filters with three scales and eight orientations is shown in Figure 2.
Entropy is a measure of the uncertainty associated with a random variable X in information theory, defined as

The less uncertainty there is, the less entropy there is. Conversely, more uncertainty produces more entropy. The objective of feature selection is to select a subset of features that gives as much information as possible. Thus, this study formulates an effective feature selection scheme based on the feature position probability distribution to select the informative Gabor features. Let  denote the occurrence of Gabor magnitude response r in
denote the occurrence of Gabor magnitude response r in  for all training images. The feature position probability is defined as
for all training images. The feature position probability is defined as

where

The entropy of the feature position probability distribution is defined as

where R is a random variable of the occurrence of Gabor magnitude response. The value of the entropy  indicates that the uncertainty of the feature at the pixel position
indicates that the uncertainty of the feature at the pixel position  of the Gabor features with m th scale and n th orientation for all training images. A larger value of
of the Gabor features with m th scale and n th orientation for all training images. A larger value of  means that the feature magnitudes vary from different images. Thus, features along this range of the feature space can improve the discriminating power between different expression classes. On the other hand, a smaller value of the entropy
means that the feature magnitudes vary from different images. Thus, features along this range of the feature space can improve the discriminating power between different expression classes. On the other hand, a smaller value of the entropy  indicates the corresponding features tend toward the same magnitude. That is, features along this range contribute less to discrimination. To reduce the feature space, these features should not be considered in the classification phase. Accordingly, sort
indicates the corresponding features tend toward the same magnitude. That is, features along this range contribute less to discrimination. To reduce the feature space, these features should not be considered in the classification phase. Accordingly, sort  in descending order and use the first
in descending order and use the first  Gabor features as the feature vector to form a lower M-dimensional subspace, where N is the dimensionality of the original feature space and M is that of the effective feature space. Figure 3 shows an example of effective Gabor filters of a face image with three scales and eight orientations. Figure 3(a) shows the magnitudes of the Gabor features. Figure 3(b) shows the points of the top 10 percent of the Gabor features.
Gabor features as the feature vector to form a lower M-dimensional subspace, where N is the dimensionality of the original feature space and M is that of the effective feature space. Figure 3 shows an example of effective Gabor filters of a face image with three scales and eight orientations. Figure 3(a) shows the magnitudes of the Gabor features. Figure 3(b) shows the points of the top 10 percent of the Gabor features.
3.3. RDA-Based Boosting Algorithm
RDA combines the strengths of LDA and QDA, offering several advantages compared to the conventional LDA and QDA. LDA and QDA are well known and popular methods in classification and recognition. However, these approaches often suffer from the small sample size problem (SSS) that exists in high-dimensional pattern recognition tasks. To solve the SSS problem, the traditional solution adopts a two-phase framework PCA plus LDA for feature compression and selection. However, the PCA may discard dimensions that contain important discriminative information [31]. Thus RDA, an intermediate method between LDA and QDA, is proposed to deal with this problem [32].
3.3.1. Regularized Discriminant Analysis
Given a set of objects  , the purpose of classification or discriminant is to assign objects to one of several K classes. The classification rule is based on a quantity called the discriminant score for the k th class, defined as
, the purpose of classification or discriminant is to assign objects to one of several K classes. The classification rule is based on a quantity called the discriminant score for the k th class, defined as

with

where k denotes the k th class, and  and
and  are mean and covariance matrix of the k th class, respectively. In the case of LDA, variables are normally distributed in each class with different mean vectors and a common covariance matrix. On the other hand, the variables in QDA are assumed to be normally distributed in each class with different mean vectors and different covariance matrices.
are mean and covariance matrix of the k th class, respectively. In the case of LDA, variables are normally distributed in each class with different mean vectors and a common covariance matrix. On the other hand, the variables in QDA are assumed to be normally distributed in each class with different mean vectors and different covariance matrices.
Compared with LDA, which shares the same covariance structure between different classes, QDA better fits the data distribution because it allows for different covariance matrices. However, QDA needs more parameters to estimate covariance matrices. Hence, classification based on QDA requires larger samples than those based on LDA. Additionally, in small-sample classification, reducing the number of estimated parameters by using the pooled covariance estimate may lead to superior performance, even if the class covariance matrices are substantially different. That is, LDA generally outperforms QDA in SSS problems. For these reasons, RDA provides a regularization mechanism to shrink the separate covariance of QDA toward a common covariance as in LDA. The regularized covariance matrix of k th class is

where  is the covariance of the k th class and
is the covariance of the k th class and  is the pooled covariance matrix used in LDA, which is also known as the within-class scatter matrix. However, the regularization in (12) is not enough. If the total sample size, n, is less than the data dimensionality, QDA and LDA are ill-posed. Additionally, biasing the class covariance matrices toward commonality may not be an effective shrinkage way. According to [33], ridge regression regularizes ordinary linear least squares regression by shrinking toward a multiple of the identity matrix. Therefore, the regularization should be
is the pooled covariance matrix used in LDA, which is also known as the within-class scatter matrix. However, the regularization in (12) is not enough. If the total sample size, n, is less than the data dimensionality, QDA and LDA are ill-posed. Additionally, biasing the class covariance matrices toward commonality may not be an effective shrinkage way. According to [33], ridge regression regularizes ordinary linear least squares regression by shrinking toward a multiple of the identity matrix. Therefore, the regularization should be

where  is an identity matrix of size d by d and d is the dimensionality of the data. The terms
is an identity matrix of size d by d and d is the dimensionality of the data. The terms  and
and  represent two parameters that range from 0 to 1.
represent two parameters that range from 0 to 1.
RDA provides a fairly rich class of regularization alternatives. Figure 4 shows four corners in the  plane representing well-known classification procedures. The lower left corner
plane representing well-known classification procedures. The lower left corner  represents QDA. The lower right
represents QDA. The lower right  represents LDA. The upper right corner
represents LDA. The upper right corner  corresponds to the nearest-means classifier. The upper left corner of the plane represents a weighted nearest-means classifier.
corresponds to the nearest-means classifier. The upper left corner of the plane represents a weighted nearest-means classifier.
3.3.2. Model Selection
A good pair of values for  and
and  is not likely to be known in advance. Selecting an optimal value for a parameter pair such as
is not likely to be known in advance. Selecting an optimal value for a parameter pair such as  is called model selection. Because model selection is a type of optimization problem, this study uses a PSO algorithm [34] to obtain the optimal parameters. The basic concept of PSO algorithm is described as follows.
is called model selection. Because model selection is a type of optimization problem, this study uses a PSO algorithm [34] to obtain the optimal parameters. The basic concept of PSO algorithm is described as follows.
Suppose that the i th particle of the swarm is denoted by  , and the velocity vector of the i th particle is denoted by
, and the velocity vector of the i th particle is denoted by  . Equations (14) shows the particle position and the velocity vector updating:
. Equations (14) shows the particle position and the velocity vector updating:

where  is a random number generated within (0,1). The terms
is a random number generated within (0,1). The terms  and
and  are positive constant parameters which control the maximum step size.
are positive constant parameters which control the maximum step size.  is the best solution achieved so far by
is the best solution achieved so far by  particle, and
particle, and  is the best solution achieved so far for the whole particles. The velocity vector
is the best solution achieved so far for the whole particles. The velocity vector  is confined within
is confined within  , and it is set equal to the corresponding threshold if the velocity vector exceeds the threshold
, and it is set equal to the corresponding threshold if the velocity vector exceeds the threshold  or
or  . The PSO procedure is given as follows.
. The PSO procedure is given as follows.
-
(1)
Randomly initialize
 and
and  of all particles.
of all particles. -
(2)
Evaluate the fitness values of all particles, and update
 and
and 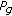 .
. -
(3)
Update
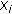 and
and 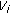 according to (14).
according to (14). -
(4)
Evaluate the fitness values of all particles, and update
 and
and 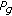 .
. -
(5)
If the convergence condition is not reached, go back to step (3).
3.3.3. Boosting Procedure
The ability of a boosting algorithm to reduce the overfitting and generalization errors of classification problems is quite interesting. In the traditional AdaBoost algorithm, the learner is weak and just slightly better than random guessing. In contrast, the proposed RDA-based boosting algorithm uses Direct LDA (DLDA) [35] to reduce dimensionality and extract discriminative features. RDA then performs the classification tasks.
Algorithm 1 illustrates the proposed RDA-based boosting algorithm. Given a training set  , containing C classes, each class
, containing C classes, each class  consists of a number of examples
consists of a number of examples  and their corresponding class labels
and their corresponding class labels  .
.  is the total number of examples in the set. Let X be the sample space:
is the total number of examples in the set. Let X be the sample space:  and at
and at  be the label set:
be the label set:  . The goal of learning is to estimate a classifier
. The goal of learning is to estimate a classifier  , which will correctly classify unseen examples. It works by repeatedly applying a given learner to a weighted version of the training set in T iterations and combining these learners
, which will correctly classify unseen examples. It works by repeatedly applying a given learner to a weighted version of the training set in T iterations and combining these learners  at each iteration into a single strong classifier.
at each iteration into a single strong classifier.
Algorithm 1: RDA-based boosting algorithm
( ) Given set of training images
) Given set of training images  with labels
with labels  , where
, where  ;
;
a DLDA feature extractor and an RDA-based learner; and the iteration number, T. Let 
( ) Initialize
) Initialize  , the mislabel distribution over B.
, the mislabel distribution over B.
( ) For
) For  , repeat the following steps:
, repeat the following steps:
(a) Update the pseudo sample distribution: 
(b) If  : randomly choose n samples per class to form a learning set
: randomly choose n samples per class to form a learning set 
(c) else: choose n hardest samples per class based on  to form
to form 
(d) Train a DLDA feature extractor P, which is a projection matrix, to obtain discriminative feature set ( )
)
(e) Use PSO to find the optimal parameters  of covariance matrix in RDA.
of covariance matrix in RDA.
(f) Build an RDA learner  , apply it into the entire training set X, and normalize the classified result
, apply it into the entire training set X, and normalize the classified result
from 0 to 1 by  .
.
(g) Calculate the pseudo-loss produced by  :
: 
(h) Set  . If
. If  , then
, then  and abort loop.
and abort loop.
(i) Update the mislabel distribution 
(j) Normalize  so that it is a distribution,
so that it is a distribution, 
( ) Output the final composite classifier
) Output the final composite classifier 
4. Experiment Results
The current study evaluates the proposed algorithm using the JAFFE database (Figure 5) which is commonly used for facial expression recognition tasks. The database includes 210 facial expression images of ten people. Each person has seven expressions (anger, disgust, fear, happiness, sadness, surprise, and the neutral state) and there are three examples of each expression. These images are grayscale and have a resolution of  . In the preprocessing step, face images are detected by the Viola and Jones face detector, cropped, and resized to
. In the preprocessing step, face images are detected by the Viola and Jones face detector, cropped, and resized to  Histogram equalization is then applied to eliminate the illumination variation. Afterwards, the resolution of the face images is downsampled to
Histogram equalization is then applied to eliminate the illumination variation. Afterwards, the resolution of the face images is downsampled to  .
.
The current study uses the leave-one-out strategy in the training procedure, as in [18]. The database is divided randomly into thirty segments for each expression. Then, twenty-nine segments per class are used to train and the remaining segment is used to test. The procedure of training and testing is repeated thirty times until each segment has been used in test. Finally, all the recognition rates are averaged to obtain an overall recognition rate for the proposed method.
The performance of the proposed system can be affected by two factors. One is the effective Gabor feature selection and the other is the number of hardest-to-classify samples in RDAB algorithm. Table 1 compares different levels of the effective Gabor features. Results show that the top ten percent of the selected Gabor features with three scales and eight orientations achieve the highest recognition rate of 96.67%. This means that there was a 10-fold reduction in the number of Gabor filters used. The results also clearly show that the Gabor features with three scales and eight orientations outperform those with five scales and eight orientations. In this experiment, the number of iterations in RDAB algorithm is 25. The number of hardest-to-classify images per class is 12.
The RDAB algorithm selects many hardest-to-classify samples to train the learner in each iteration. The number of hardest-to-classify samples affects the learner's capacity. Consequently, the optimal number of hardest-to-classify samples can improve the classifier efficiency. Figure 6 compares the recognition rates for different numbers of hardest-to-classify samples. This figure shows that the highest recognition rate, 96.67%, is achieved when the number of hardest-to-classify is samples 12 for the top ten percent of the selected Gabor features with three scales and eight orientations. As the number of hardest-to-classify samples increases, the recognition rate decreases due to the overfitting problem. These results also indicate that Gabor features with three scales and eight orientations perform better than those with five scales and eight orientations. The number of iterations in RDAB algorithm in this experiment is 25, and the top ten percent of the selected Gabor features are used.
It is not easy to directly compare our results with others because different research groups conducted different types of tests using different data sets. As mentioned in the introduction, previous experiments can be classified into two main categories: those using static images or image sequences. This study only compares experiments using JAFFE static images, as Table 2 shows. In [17], facial expression classification performance was tested on feature vectors derived from two-dimensional discriminant locality preserving projections, producing a 95.91% recognition rate. Shin et al. [18] investigated various feature representation and expression classification schemes to recognize seven different facial expressions. Their experiment results show that the method of combining 2D-LDA (Linear Discriminant Analysis) and SVM outperforms other methods, producing a 95.71% recognition rate using the leave-one-out strategy. Feng et al. [19] reported an accuracy of 93.8% based on local binary pattern histograms and linear programming techniques. In [36], a method for facial expression recognition with Non-negative Matrix Factorization (NMF) and PCA-NMF is presented, and their best recognition rate is 93.72%. The work reported in [37, 38] produced recognition rates of 94.64% and 95.7%, respectively. In this study, we use a leave-one-out strategy similar to that in [18] to verify our algorithm. Our recognition rate of 96.67% outperforms other methods tested on the same database. Table 3 shows the confusion matrix, indicating that anger, happiness, and the neutral state are recognized with very high accuracy, but other expressions (disgust, fear, sadness, surprise) are sometimes confused.
5. Conclusion
This paper proposes a novel facial expression recognition method based on RDA and a boosting algorithm. Since full facial images provide confusing and redundant information for identifying facial expressions, this study proposes an effective Gabor feature selection based on an entropy criterion. This effective Gabor feature is a subset of informative and nonredundant Gabor features. This approach reduces the feature dimensionality without losing much information and decreases computation and storage requirements. This study adopts RDA as a learner in the boosting algorithm. RDA provides a regularization technique to combine the strengths of QDA and LDA. Meanwhile, a PSO algorithm is adopted to cope with the modal selection problem in RDA. The results of this study show that the proposed method has a high recognition rate of 96.67%, which is better than other reported results. The confusion matrix also shows that anger, happiness, and the neutral state are recognized with very high accuracy.
References
Pantic M, Pentland A, Nijholt A, Huang T: Human computing and machine understanding of human behavior: a survey. Proceedings of the 8th International Conference on Multimodal Interfaces (ICMI '06), 2006 239-248.
Zeng Z, Pantic M, Roisman GI, Huang TS: A survey of affect recognition methods: audio, visual, and spontaneous expressions. IEEE Transactions on Pattern Analysis and Machine Intelligence 2009, 31(1):39-58.
Mehrabian A: Communication without words. Psychology Today 1968, 2(4):53-56.
Samal A, Iyengar PA: Automatic recognition and analysis of human faces and facial expressions: a survey. Pattern Recognition 1992, 25(1):65-77. 10.1016/0031-3203(92)90007-6
Pantic M, Rothkrantz LJM: Automatic analysis of facial expressions: the state of the art. IEEE Transactions on Pattern Analysis and Machine Intelligence 2000, 22(12):1424-1445. 10.1109/34.895976
Fasel B, Luettin J: Automatic facial expression analysis: a survey. Pattern Recognition 2003, 36(1):259-275. 10.1016/S0031-3203(02)00052-3
Pantic M, Bartlett MS: Machine Analysis of Facial Expressions, Face Recognition. I-Tech Education and Publishing; 2007.
Darwin C: The Expression of Emotions in Man and Animals. John Murray, London, UK; 1965. reprinted by University of Chicago Press
Keltner D, Ekman P: Facial expression of emotion. In Handbook of Emotions. Edited by: Lewis M, Haviland-Jones JM. Guilford, New York, NY, USA; 2000:236-249.
Ekman P, Friesen WV: The Facial Action Coding System: A Technique for the Measurement of Facial Movement. Edited by: Francisco M. Consulting Psychologists Press; 1978.
Donato G, Bartlett MS, Hager JC, Ekman P, Sejnowski TJ: Classifying facial actions. IEEE Transactions on Pattern Analysis and Machine Intelligence 1999, 21(10):974-989. 10.1109/34.799905
Yacoob Y, Davis L: Recognizing faces showing expressions. Proceedings of the International Workshop on Automatic Face and Gesture Recognition, 1995 278-283.
Bartlett MS, Hager JC, Ekman P, Sejnowski TJ: Measuring facial expressions by computer image analysis. Psychophysiology 1999, 36(2):253-263. 10.1017/S0048577299971664
Essa IA, Pentland AP: Coding, analysis, interpretation, and recognition of facial expressions. IEEE Transactions on Pattern Analysis and Machine Intelligence 1997, 19(7):757-763. 10.1109/34.598232
Xiang T, Leung MKH, Cho SY: Expression recognition using fuzzy spatio-temporal modeling. Pattern Recognition 2008, 41(1):204-216. 10.1016/j.patcog.2007.04.021
Chen XW, Huang T: Facial expression recognition: a clustering-based approach. Pattern Recognition Letters 2003, 24(9-10):1295-1302. 10.1016/S0167-8655(02)00371-9
Zhi R, Ruan Q: Facial expression recognition based on two-dimensional discriminant locality preserving projections. Neurocomputing 2008, 71(7–9):1730-1734.
Shin FY, Chuang CF, Wang PSP: Performance comparisons of facial expression recognition in JAFFE database. International Journal of Pattern Recognition and Artificial Intelligence 2008, 22(3):445-459. 10.1142/S0218001408006284
Feng X, Pietikäinen M, Hadid A: Facial expression recognition based on local binary patterns. Pattern Recognition and Image Analysis 2007, 17(4):592-598. 10.1134/S1054661807040190
Viola P, Jones M: Rapid object detection using a boosted cascade of simple features. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2001 1: 511-518.
Xu Y, Jin Z: Down-sampling face images and low-resolution face recognition. Proceedings of the 3rd International Conference on Innovative Computing Information and Control (ICICIC '08), 2008 392.
Daugman JG: Complete discrete 2-D Gabor transforms by neural networks for image analysis and compression. IEEE Transactions on Acoustics, Speech, and Signal Processing 1988, 36(7):1169-1179. 10.1109/29.1644
Tsai CC, Taur J, Tao CW: Iris recognition based on relative variation analysis with feature selection. Optical Engineering 2008., 47(9):
Zhang B, Wang Z, Zhong B: Kernel learning of histogram of local Gabor phase patterns for face recognition. EURASIP Journal on Advances in Signal Processing 2008, 2008:-8.
Liu DH, Lam KM, Shen LS: Optimal sampling of Gabor features for face recognition. Pattern Recognition Letters 2004, 25(2):267-276. 10.1016/j.patrec.2003.10.007
Littlewort G, Bartlett MS, Fasel I, Susskind J, Movellan J: Dynamics of facial expression extracted automatically from video. Image and Vision Computing 2006, 24(6):615-625. 10.1016/j.imavis.2005.09.011
Shen L, Bai L: Information theory for Gabor feature selection for face recognition. EURASIP Journal on Applied Signal Processing 2006, 2006:-11.
Shen L, Bai L, Bardsley D, Wang Y: Gabor feature selection for face recognition using improved AdaBoost learning. Proceedings of the International Wokshop on Biometric Recognition Systems (IWBRS '05), October 2005, Beijing, China, Lecture Notes in Computer Science 3781: 39-49.
Yang P, Liu Q, Metaxas DN: Boosting encoded dynamic features for facial expression recognition. Pattern Recognition Letters 2009, 30(2):132-139. 10.1016/j.patrec.2008.03.014
Lu J, Plataniotis KN, Venetsanopoulos AN, Li SZ: Ensemble-based discriminant learning with boosting for face recognition. IEEE Transactions on Neural Networks 2006, 17(1):166-178.
Chen L-F, Liao H-YM, Ko M-T, Lin J-C, Yu G-J: New LDA-based face recognition system which can solve the small sample size problem. Pattern Recognition 2000, 33(10):1713-1726. 10.1016/S0031-3203(99)00139-9
Friedman JH: Regularized discriminant analysis. Journal of the American Statistical Association 1989, 84(405):165-175. 10.2307/2289860
Hoerl A, Kennard R: Ridge regression: biased estimation for non-orthogonal problems. Technometrics 1970, 12(3):55-67.
Kennedy J, Eberhart R: Particle swarm optimization. Proceedings of the IEEE International Conference on Neural Networks, 1995 4: 1942-1948.
Yu H, Yang J: A direct LDA algorithm for high-dimensional data with application to face recognition. Pattern Recognition 2001, 34: 2067-2070. 10.1016/S0031-3203(00)00162-X
Zhao L, Zhuang G, Xu X: Facial expression recognition based on PCA and NMF. Proceedings of the World Congress on Intelligent Control and Automation (WCICA '08), 2008 6822-6825.
Qi XX, Jiang W: Application of wavelet energy feature in facial expression recognition. Proceedings of the IEEE International Workshop on Anti-Counterfeiting, Security, Identification (ASID '07), 2007 169-174.
Liejun W, Xizhong Q, Taiyi Z: Facial expression recognition using improved support vector machine by modifying kernels. Information Technology Journal 2009, 8(4):595-599. 10.3923/itj.2009.595.599
Acknowledgment
The authors would like to thank the National Science Council (Grant no. NSC 98-2221-E-155-050) for supporting this work.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lee, CC., Huang, SS. & Shih, CY. Facial Affect Recognition Using Regularized Discriminant Analysis-Based Algorithms. EURASIP J. Adv. Signal Process. 2010, 596842 (2010). https://doi.org/10.1155/2010/596842
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/596842




 represents QDA,
represents QDA,  represents LDA,
represents LDA,  corresponds to the nearest-means classifier, and
corresponds to the nearest-means classifier, and  represents a weighted nearest-means classifier.
represents a weighted nearest-means classifier. and
and  of all particles.
of all particles. and
and 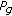 .
.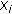 and
and 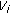 according to (14).
according to (14). and
and 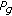 .
.
