- Research Article
- Open access
- Published:
Approximate Minimum Bit Error Rate Equalization for Fading Channels
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 615623 (2010)
Abstract
A novel channel equalizer algorithm is introduced for wireless communication systems to combat channel distortions resulting from multipath propagation. The novel algorithm is based on minimizing the bit error rate (BER) using a fast approximation of its gradient with respect to the equalizer coefficients. This approximation is obtained by estimating the exponential summation in the gradient with only some carefully chosen dominant terms. The paper derives an algorithm to calculate these dominant terms in real-time. Summing only these dominant terms provides a highly accurate approximation of the true gradient. Combined with a fast adaptive channel state estimator, the new equalization algorithm yields better performance than the traditional zero forcing (ZF) or minimum mean square error (MMSE) equalizers. The performance of the new method is tested by simulations performed on standard wireless channels. From the performance analysis one can infer that the new equalizer is capable of efficient channel equalization and maintaining a relatively low bit error probability in the case of channels corrupted by frequency selectivity. Hence, the new algorithm can contribute to ensuring QoS communication over highly distorted channels.
1. Introduction
Broadband radio channels are susceptible to selective fading due to multipath propagation. In this case, the differences among the propagation delays on the paths may amount to a significant fraction of a symbol interval. Hence, frequency selective fading may yield severe performance degradation. As a result, efficient channel equalization techniques prove to be instrumental to combat intersymbol interference (ISI) in order to avoid large scale drops in system performance.
Since the effect of interferences are especially crucial in wireless communication systems, fast channel equalizer algorithms have to be developed which are simple enough to run on the currently available hardware architectures. This paper aims at developing a low complexity channel equalizer algorithm by directly minimizing the BER instead of minimizing the mean-square error or the peak distortion [1, 2]. Unfortunately, the direct minimization of BER with respect to the equalizer coefficients is of exponential complexity due to the large summation when expressing BER as a function of the equalizer coefficients. Thus, we develop a new bound on BER on which basis the equalizer coefficients can be optimized by a fast algorithms. It is also pointed out that the new bound on BER is sharper than the previously known ones listed in [3].
The first attempts to derive an equalizer based on the minimum BER strategy can be found in the work of Shimbo and Celebiler [4] and Shamas and Yao [5]. The optimal equalizer coefficients were only sought by exhaustive search, thus real-time adaptivity was not guaranteed. In recent years, some new results have been developed for minimum BER equalization. In [6], a low-complexity adaptive algorithm is proposed for 2- or 4-state modulation systems but the convergence is rather slow, while in [7, 8] near minimum BER equalization is carried out by radial basis function neural networks which considerably increases the equalizer complexity. On the other hand, very complex equalizer schemes have been proposed for DS-CDMA systems in [9–11]. Paper [12] investigates the minimization of BER in MIMO systems with linear equalizers based on QPSK modulation. In this model the information sequence is corrupted by multiuser interference and additive noise. BER is derived for the case of two transmitters and approximated by a simple formula. The optimum then is calculated by analytical tools. When the number of transmitters is larger than two then the authors use a sequence of cascade filters. It is important to note that this article does not address the problem of ISI. In paper [13], BER is minimized subject to some constraints. The authors prove that the constrained BER cost function has only one global minimum and equalization can be achieved by quadratic programming. However, due to the constraints this detector is only optimal in the case of minimum phase channels. In the paper [14, 15], the equalization is carried out by using the Bayes risk criterion. This is a more general approach than BER minimization, but the choice of loss function is left open, realizing that not every loss function will yield fast convergence or yield low error rate. Furthermore, the loss function is very complex and does not lend itself to simple minimization. Therefore, deriving bound on BER for fast minimization with respect to the equalizer coefficients can still yield powerful and real-time channel equalization. The novel algorithm presented by the paper is demonstrated by BPSK modulation scheme.
The results are given in the following structure:
-
(i)
in Section 2, the communication model is outlined;
-
(ii)
in Section 3, BER is expressed as a function of the equalizer coefficients and a gradient based algorithm is discussed for minimizing BER;
-
(iii)
in Section 4, a novel method is derived to approximate BER by using the dominant terms;
-
(iv)
in Section 5, the new equalizer algorithm will be introduced based on the approximation treated in Section 4;
-
(v)
in Section 6, the performance and convergence properties of the new equalizer algorithms are analyzed numerically.
2. The Model
To describe single-user communication over a fading channel, we use the so-called equivalent discrete time white noise filter model (for further details see [1]).
The corresponding quantities are defined as follows:

 denotes the transmitted information bit at time instant
denotes the transmitted information bit at time instant  being a sequence of identically distributed independent Bernoulli random variables with
being a sequence of identically distributed independent Bernoulli random variables with  ;
;
 the discrete impulse response of the channel is denoted by
the discrete impulse response of the channel is denoted by  where
where  denotes the span of ISI;
denotes the span of ISI;
 the noise is denoted by
the noise is denoted by  and is assumed to be a stationary zero mean white Gaussian random sequence with constant spectral density
and is assumed to be a stationary zero mean white Gaussian random sequence with constant spectral density  ;
;
 the received sequence is denoted by
the received sequence is denoted by  , which is a linearly distorted and noisy version of the transmitted sequence given as
, which is a linearly distorted and noisy version of the transmitted sequence given as

 the equalizer is a linear FIR filter, the output of which is denoted by
the equalizer is a linear FIR filter, the output of which is denoted by 

where 
 denotes the free parameters of the equalizer which are subject to further optimization;
denotes the free parameters of the equalizer which are subject to further optimization;
 the decision is carried out by threshold detection in a symbol-by-symbol fashion:
the decision is carried out by threshold detection in a symbol-by-symbol fashion:

where  denotes the delay of the channel. (For the sake of brevity, here we assume
denotes the delay of the channel. (For the sake of brevity, here we assume  , while the more general treatment for
, while the more general treatment for  will be given in Section 4.3);
will be given in Section 4.3);
 the overall channel impulse response function is determined by the cascade of the channel and the equalizer
the overall channel impulse response function is determined by the cascade of the channel and the equalizer

where  denotes the support of the overall impulse response.
denotes the support of the overall impulse response.
Traditional equalization algorithms aimed at minimizing the peak distortion [1, 16] defined as

or the mean-square error [1, 2]

Both approaches involve the use of linear stochastic approximation schemes [1, 2, 16], but they fell short of providing efficient equalization as the goal functions did not have any direct relationship with BER.
3. Weight Optimization Subject to Minimizing the BER
Since our approach to equalization is based on minimizing the bit error probability, first we express BER as a function of the equalizer coefficients as given in [4]

where  denotes the standard normal cumulative distribution function,
denotes the standard normal cumulative distribution function,  , and
, and  . Here, we note that in the paper, for expressing the BER, we will use the standard Gaussian distribution function defined as
. Here, we note that in the paper, for expressing the BER, we will use the standard Gaussian distribution function defined as  . The relationships of
. The relationships of  with the
with the  function
function  and the error function
and the error function  are given as follows:
are given as follows:  and
and  . Substituting (4) into (7), we obtain
. Substituting (4) into (7), we obtain

To find the optimal weights of the equalizer which minimize this error probability, we have to solve the following equation:

where the  th component of the gradient is
th component of the gradient is

The weights can be optimized by gradient descent, yielding the following equalization algorithm:

Here,  is the value of the weight vector at the
is the value of the weight vector at the  th iteration. One must note, that the gradient search with fixed step size in general will not guarantee the convergence to the global minimum. However, as our simulations have demonstrated, over standard wireless channels the algorithm in most cases reached the global optimum.
th iteration. One must note, that the gradient search with fixed step size in general will not guarantee the convergence to the global minimum. However, as our simulations have demonstrated, over standard wireless channels the algorithm in most cases reached the global optimum.
In the forthcoming discussion, the procedure given by formula (11) is termed as true gradient search (TGS). Unfortunately performing TGS is computationally prohibitive, because of the summation over an exponentially large number of vectors in expression (10). Furthermore, this summation in TGS must be calculated in each step of algorithm (11). Thus, TGS can only be applied in practice if the support of the overall impulse response defined in (4) is very limited. Otherwise, near-optimal algorithms must be sought which lend themselves to real-time implementations. To ease this complexity a new bound is derived on BER.
4. New Lower Bound on BER by Using the Dominant Terms
In this section, we derive a new approximation on BER. The purpose of developing this approximation is to estimate BER with an expression which is a computationally simple function of the equalizer weights. This paves the way towards real-time channel equalization.
In order to derive a bound on BER, one can note that function  tends rapidly to zero for negative arguments. As a result, the terms in the summation can differ in several magnitudes. This gives rise to the idea of collecting only the dominant terms to provide a lower bound on BER. This lower bound has been commonly used in other domains, such as reliability analysis and referred to as Li-Silvester bound [17], where the tiresome calculation of an expected value over a large state space is approximated by only using the dominant terms in the summation.
tends rapidly to zero for negative arguments. As a result, the terms in the summation can differ in several magnitudes. This gives rise to the idea of collecting only the dominant terms to provide a lower bound on BER. This lower bound has been commonly used in other domains, such as reliability analysis and referred to as Li-Silvester bound [17], where the tiresome calculation of an expected value over a large state space is approximated by only using the dominant terms in the summation.
In our case, this bound can be obtained as follows. We may look upon (8) as an expected value, given as follows:

Introducing the following notations, one can obtain

Let us then separate the set  into two disjoint subsets
into two disjoint subsets  and
and  (
(  ,
,  ). Let the number of elements in
). Let the number of elements in  be
be  , containing the first
, containing the first  vectors belonging to the first
vectors belonging to the first  largest values of
largest values of  , for which
, for which

From the properties of  it follows that
it follows that  . This gives rise to the following bounds on BER:
. This gives rise to the following bounds on BER:

yielding

where  denotes the cardinality of
denotes the cardinality of  .
.
Remark 4.
In this case,  is subject to uniform distribution, thus the left hand side of (15) can be very tight if
is subject to uniform distribution, thus the left hand side of (15) can be very tight if  is chosen reasonably high. At the same time, the upper bound tends to be loose as the terms
is chosen reasonably high. At the same time, the upper bound tends to be loose as the terms  in
in  have rather inaccurate upperbounds. In Section 4.2, we will evaluate the tightness of the bound based on the
have rather inaccurate upperbounds. In Section 4.2, we will evaluate the tightness of the bound based on the  th dominant sample.
th dominant sample.
The most "harmful" sequence, denoted by  in
in  (i.e., the sequences beginning with
(i.e., the sequences beginning with  ) is
) is  since
since  , which indicates
, which indicates  to be the absolute dominant term in the summation equation (12).
to be the absolute dominant term in the summation equation (12).
In order to determine the dominant terms that form the set  , let us introduce the following notation: let
, let us introduce the following notation: let  be an index array pointing to the different elements of
be an index array pointing to the different elements of  , where
, where

Note that  points to the
points to the  th smallest element of
th smallest element of  in absolute value. The extension of index array
in absolute value. The extension of index array  for
for  will be given in Section 4.3. The second dominant term
will be given in Section 4.3. The second dominant term  can be deduced from
can be deduced from  by changing the sign of the component
by changing the sign of the component  , because in this case
, because in this case  , where
, where  is the smallest possible value for decreasing the PD.
is the smallest possible value for decreasing the PD.
Applying the same reasoning, the first  largest terms can be given as follows:
largest terms can be given as follows:
-
(1)
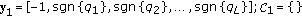 ;
; -
(2)
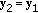 and change the sign of the component
and change the sign of the component  ;
; -
(3)
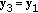 and change the sign of the component of
and change the sign of the component of 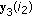 ;
; 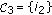 ;
; -
(4)
FOR
 TO
TO  find the index set
find the index set  for which
for which 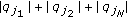 is minimal, but
is minimal, but 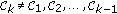 and
and  ;
; -
(5)
Form the set
 to be used in the lower bound given in (16).
to be used in the lower bound given in (16).
It is easy to see that the case of  (when
(when  ) results in a cost function which has minimum value over the same coefficient vector as has the peak distortion. Increasing the value of
) results in a cost function which has minimum value over the same coefficient vector as has the peak distortion. Increasing the value of  , the lower bound in (16) tends to the exact
, the lower bound in (16) tends to the exact  and finally the case of
and finally the case of  and
and  results in the exact minimum of BER.
results in the exact minimum of BER.
We generally can derive an algorithm which identifies the dominant terms for any arbitrary  where
where  . The following procedure results in the first 4 dominant terms, which seems practically to be a good compromise between
. The following procedure results in the first 4 dominant terms, which seems practically to be a good compromise between  (yielding the PD criterion) and
(yielding the PD criterion) and  (for further details, see Section 4.2):
(for further details, see Section 4.2):
-
(1)
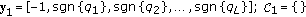 ;
; -
(2)
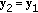 and change the sign of the component
and change the sign of the component 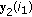 ;
; 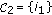 ;
; -
(3)
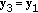 and change the sign of the component
and change the sign of the component 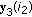 ;
; 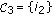 ;
; -
(4)
If
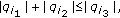 then
then  and change the sign of the components
and change the sign of the components  and
and 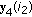 ;
; 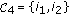 ; ELSE
; ELSE 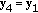 and change the sign of the component
and change the sign of the component 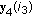 ;
; 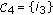 ;
; -
(5)
Form the set
 to be used in the lower bound (16).
to be used in the lower bound (16).
Unfortunately, calculating the set  to find the
to find the  largest term is of exponential complexity, as
largest term is of exponential complexity, as  must be calculated and arranged in monotone order for all possible
must be calculated and arranged in monotone order for all possible  .
.
4.1. Optimization of the Bound
The gradient  of the lower bound in (16) is a truncated version of the gradient of the true BER (10), obtained by carrying out the summation over
of the lower bound in (16) is a truncated version of the gradient of the true BER (10), obtained by carrying out the summation over  instead of
instead of  :
:

Using the gradient, the following adaptive algorithm can be used for weight optimization

Of course, one can use variable step size  in algorithm (19) to improve the speed of convergence. For example, the Armijo rule [15] can be applied to speed up the convergence. However, simulations showed no improvement by applying this rule. Another problem with this method is its high complexity (the gradient has to be evaluated several times). On the other hand, we may introduce a heuristically chosen step size, such as
in algorithm (19) to improve the speed of convergence. For example, the Armijo rule [15] can be applied to speed up the convergence. However, simulations showed no improvement by applying this rule. Another problem with this method is its high complexity (the gradient has to be evaluated several times). On the other hand, we may introduce a heuristically chosen step size, such as  . The convergence of (19) by using this step size this algorithm is guaranteed by the Kushner-Clark theorem (for more details, see [16]). In the simulation section, the improvement of convergence achieved by variable step size method is also illustrated.
. The convergence of (19) by using this step size this algorithm is guaranteed by the Kushner-Clark theorem (for more details, see [16]). In the simulation section, the improvement of convergence achieved by variable step size method is also illustrated.
4.2. A Numerical Example for Calculating the New Bound
For the sake of better understanding of the algorithm developed for finding the dominant terms, a numerical example will be given as follows. Let us take the following overall impulse response function

where  . At first, the index array
. At first, the index array  will be defined containing the indices of the smallest, second smallest, and so forth. elements of
will be defined containing the indices of the smallest, second smallest, and so forth. elements of  (omitting
(omitting  ), respectively:
), respectively:

The information sequence resulting in maximum distortion, can be calculated as

yielding

The information sequence  can be derived from
can be derived from  changing the sign of the element
changing the sign of the element  :
:

resulting in

and  comes from
comes from  by changing the sign of the element
by changing the sign of the element 

yielding

To determine  , one can evaluate the sum
, one can evaluate the sum  . Since it is smaller than
. Since it is smaller than  ,
,  can be derived from
can be derived from  by changing the sign of the elements
by changing the sign of the elements  and
and  :
:

resulting in

If one calculates all possible terms up to  (which equals
(which equals  ), the bit error probability can be calculated using (12) as
), the bit error probability can be calculated using (12) as

In Figure 1, one can see the terms  versus
versus  for two different
for two different  values. In this figure, logarithmic scale on the vertical axis was used, and smaller values than
values. In this figure, logarithmic scale on the vertical axis was used, and smaller values than  were omitted. Note that the number of negligible terms depends on the noise level. This is explained by the fact that increasing the noise level, the samples
were omitted. Note that the number of negligible terms depends on the noise level. This is explained by the fact that increasing the noise level, the samples  will fall into a region where
will fall into a region where  decreases rather fast. The difference between the smallest and largest terms is of
decreases rather fast. The difference between the smallest and largest terms is of  magnitudes. Furthermore, one may note that there are no
magnitudes. Furthermore, one may note that there are no  samples on the positive side which proves that channel can indeed be equalized and in this case there are no local minima as proven in [13].
samples on the positive side which proves that channel can indeed be equalized and in this case there are no local minima as proven in [13].
In order to derive a method to identify  first let us express the bit error probability as a sum of two expressions
first let us express the bit error probability as a sum of two expressions

where the second term can be upper bounded by using the  th dominant sample. In this way, one obtains the following bound:
th dominant sample. In this way, one obtains the following bound:

Since the sharpness of (32) depends on the value of the ( )th dominant sample (it becomes sharp if the value of the
)th dominant sample (it becomes sharp if the value of the  th dominant sample is small), this expression can be used to estimate the number of dominant samples
th dominant sample is small), this expression can be used to estimate the number of dominant samples  to be used for giving efficient bound on BER. If the bound using the
to be used for giving efficient bound on BER. If the bound using the  th dominant sample drops below a predefined value
th dominant sample drops below a predefined value  then the number of samples
then the number of samples  needed to approximate BER can be obtained as follows:
needed to approximate BER can be obtained as follows:

where  can be substituted by its approximation using the first
can be substituted by its approximation using the first  dominant samples. Figure 2 analyzes the accuracy of the bound obtained by the dominant samples.
dominant samples. Figure 2 analyzes the accuracy of the bound obtained by the dominant samples.
Figure 2 shows two curves belonging to the  10 and 20 dB, respectively. From this figure, it can be seen that if
10 and 20 dB, respectively. From this figure, it can be seen that if  and
and  dB then the necessary number of samples
dB then the necessary number of samples  . This necessary sample number will increase with respect to the decrease of SNR (in the case of
. This necessary sample number will increase with respect to the decrease of SNR (in the case of  dB the number of samples is seven). This is in line with the reasoning detailed above.
dB the number of samples is seven). This is in line with the reasoning detailed above.
4.3. Handling the Channel Delay
If there is some delay  in the overall channel impulse response function
in the overall channel impulse response function  , a more efficient equalization can be carried out by the decision rule given in (3). The cost function based on the lower bound in (16) has only to be slightly modified in order to handling the delay parameter
, a more efficient equalization can be carried out by the decision rule given in (3). The cost function based on the lower bound in (16) has only to be slightly modified in order to handling the delay parameter  . Since in this case (instead of the first element) the
. Since in this case (instead of the first element) the  th element of
th element of  must be set to
must be set to  hence the index array used for calculating the dominant terms have to be changed to
hence the index array used for calculating the dominant terms have to be changed to

5. Obtaining Channel-State Information
In order to run the proposed algorithm, channel state information is needed (the channel impulse function  appears in expression (9)). There are plenty of real time adaptive channel identification algorithms [18] which provide fast and simple channel state information by using a training sequence
appears in expression (9)). There are plenty of real time adaptive channel identification algorithms [18] which provide fast and simple channel state information by using a training sequence  where
where  is a transmitted binary sequence known at the receiver and
is a transmitted binary sequence known at the receiver and  is the corresponding received sequence.
is the corresponding received sequence.
We identify the channel estimator with an adaptive FIR filter, the coefficients of which are updated as follows:

This algorithm minimizes the mean square error between the unknown channel impulse response function  and the FIR filter coefficients
and the FIR filter coefficients 
 . Here
. Here  denotes the received sequence at the output of the channel estimator. Parameters
denotes the received sequence at the output of the channel estimator. Parameters  in algorithm (35) converge to the true channel impulse response function
in algorithm (35) converge to the true channel impulse response function  in mean square (and in probability) if the degree of the FIR filter is larger than the channel impulse response (overmodeling).
in mean square (and in probability) if the degree of the FIR filter is larger than the channel impulse response (overmodeling).
It is noteworthy that the adaptive channel identifier (35) converges rather fast to the true cannel-state because of the narrow eigenvalue-spectrum of the underlying matrices (for further details see [1]). Hence, the combination of identification and equalization can provide real time solutions for low BER communication.
6. Numerical Results
In this section, a detailed performance analysis is given in which the bit error probability achieved by the different equalization methods are compared with each other.
6.1. Channel Characteristics and Channel-State Information
The channel distortion can be modeled by a tapped delay-line model (see Section 2). If the WSSUS (Wide Sense Stationary Uncorrelated Scattering) assumption is made, then the channel coefficient  are uncorrelated, and Gaussian distributed. In the project COST 207 [19], several wideband propagation models were proposed for the practical realization of both hardware and software simulators in the context of GSM systems for different classes of environments (an other set of models is ITU-R models for third-generation cellular systems). These models are generally described by power delay profiles from which the discrete time equivalent can be derived.
are uncorrelated, and Gaussian distributed. In the project COST 207 [19], several wideband propagation models were proposed for the practical realization of both hardware and software simulators in the context of GSM systems for different classes of environments (an other set of models is ITU-R models for third-generation cellular systems). These models are generally described by power delay profiles from which the discrete time equivalent can be derived.
The simulations were performed on three different discrete channels representing multipath propagation derived from the power delay profiles of the above mentioned models. The corresponding channel characteristics are given by their impulse response as follows: 
 ,
,  .
.
Note that channel  has the minimum-phase, while
has the minimum-phase, while  and
and  have the nonminimum-phase property. The equalization of nonminimum-phase channels is difficult, because these channels have zeros outside the unit circle, and hence, the inverse of the channel has poles outside the unit circle.
have the nonminimum-phase property. The equalization of nonminimum-phase channels is difficult, because these channels have zeros outside the unit circle, and hence, the inverse of the channel has poles outside the unit circle.
6.2. Performance Analysis
In this section we numerically investigate the BER with respect to SNR and we also analyze the convergence properties of the equalization algorithms. The abbreviations used in the figures are as follows:
-
(i)
TGS—True Gradient Search (for details see (11));
-
(ii)
LISIx—our algorithm with
 dominant terms in the approximation;
dominant terms in the approximation; -
(iii)
LMS—Least Mean Square algorithm;
-
(iv)
MMSE—Off-line calculated Minimum Mean Square Error solution
-
(v)
NOEQ—BER without any equalizer;
-
(vi)
AMBER—Adaptive Minimum Bit Error Rate algorithm [6].
As far as the channel-state information is concerned, we assumed no channel-state information to be available at the receiver side, thus channel equalization was preceded by an adaptive channel identifier algorithm given in (35). In all simulations the delay parameter  used in the decision rule (3) was set by exhaustive search. The step size of the gradient-descent-type algorithms was set empirically. The experiments show that the attained BER is not too sensitive to the value of the step size, while the convergence speed is highly dependent on this value as described below. Furthermore the value of the step size depends on the SNR as well, since the error surface tends to be more complicated as SNR increases [6].
used in the decision rule (3) was set by exhaustive search. The step size of the gradient-descent-type algorithms was set empirically. The experiments show that the attained BER is not too sensitive to the value of the step size, while the convergence speed is highly dependent on this value as described below. Furthermore the value of the step size depends on the SNR as well, since the error surface tends to be more complicated as SNR increases [6].
6.2.1. Convergence Analysis
Figure 3 demonstrates the convergence properties of the equalization algorithms. One can see, that the TGS algorithm converges rather fast; however, in each step the exponential summation have to be calculated. Algorithm LISI4 exhibits similarly fast convergence but in each step it only needs to evaluate the function  for only some dominant arguments, which results in a considerable decrease in complexity.
for only some dominant arguments, which results in a considerable decrease in complexity.
Figure 3 also demonstrates that algorithm LISI4 with fix  step size will yield slower convergence than TGS. However, the convergence speed can be increased by modifying the step size in each step according to the rule
step size will yield slower convergence than TGS. However, the convergence speed can be increased by modifying the step size in each step according to the rule  [16], which indicates that investigation on the step size can also improve the convergence.
[16], which indicates that investigation on the step size can also improve the convergence.
It is proven in [13] that in the case of nonminimum-phase channels the minimum BER error surface is convex, and hence it has only one global minimum, but in the case of nonminimum-phase channels there are local minima [6] in which gradient descent type algorithms can get stuck. In order to detect the chance to getting stuck into local minima for the channel models used in our experiments, the TGS algorithm was randomly initialized with 100 different values, and the attained BER after convergence was depicted in Figures 4, 5, and 6. These figures demonstrate that in the case of minimum-phase channel there is almost no chance of converging to local minima, while in the case of nonminimum phase channels a 5–10 percent of convergence to local minima has been detected. The problem of getting stuck into local minima can be minimized by "good" initialization, for example, iterating the equalizer weights the minimum BER algorithm can be started from an initial weight vector obtained from the MMSE solution.
6.2.2. BER versus SNR
In Figures 7–9, the BER versus SNR achieved by the classical and by the new algorithm are depicted. One can note a sharp improvement in performance achieved by the new algorithm derived from the minimum BER strategy, especially in the case of nonminimum-phase channels (such as  and
and  , see Figures 8 and 9) and good SNR circumstances. The LISI algorithm using the dominant terms performs very close to the exact minimum BER solution in the case of good SNRs, since increasing the SNR decreases the number of dominant terms, hence the bound will be sharper. On the other hand, its advantage is its low complexity against TGS (11). The AMBER algorithm introduced in performs very close to the TGS, but converges much slower than the TGS and LISI methods.
, see Figures 8 and 9) and good SNR circumstances. The LISI algorithm using the dominant terms performs very close to the exact minimum BER solution in the case of good SNRs, since increasing the SNR decreases the number of dominant terms, hence the bound will be sharper. On the other hand, its advantage is its low complexity against TGS (11). The AMBER algorithm introduced in performs very close to the TGS, but converges much slower than the TGS and LISI methods.
7. Conclusions
In this paper, a novel channel equalizer algorithm has been developed based on approximating the BER by dominant terms. Due to the simplicity of this approximation, a fast equalization algorithm can be obtained, the performance of which falls close to optimum. Since this approximation needs channel state information, the equalizer is preceded by an adaptive channel identifier. The combined convergence of channel identification and the new bound-based equalization is still much faster than the convergence of other algorithms (e.g., LMS, AMBER [6]). The operational complexity of the new algorithm is also smaller than TGS (for details see (11)). The new method yielded better performance than the traditional ZF and MMSE equalizer algorithms on standard wireless channels. These benefits make the new algorithm suitable for real time applications.
References
Proakis J: Digital Communications. 4th edition. McGraw–Hill, New York, NY, USA; 2001.
Biglieri E, Proakis J, Shamai S: Fading channels: information-theoretic and communications aspects. IEEE Transactions on Information Theory 1998, 44(6):2619-2692. 10.1109/18.720551
Glave FE: An upper bound on the probability of error due to intersymbol interference for correlated digital signals. IEEE Transactions on Information Theory 1972, 18(3):356-363. 10.1109/TIT.1972.1054828
Shimbo SO, Celebiler M: The probability of error due to intersymbol interference and gaussian noise in digital communication systems. IEEE Transactions on Communications 1971, 19(2):113-119. 10.1109/TCOM.1971.1090619
Shamash E, Yao K: On the structure and performance of a linear decision feedback equalizer based on the minimum error probability criterion. Proceedings of the 10th International Conference on Communications (ICC '74), 1974, Minneapolis, Minn, USA 1-5.
Yeh C-C, Barry JR: Adaptive minimum bit-error rate equalization for binary signaling. IEEE Transactions on Communications 2000, 48(7):1226-1235. 10.1109/26.855530
Chen S, Mulgrew B, Hanzo L: Least bit error rate adaptive nonlinear equalisers for binary signalling. IEE Proceedings: Communications 2003, 150(1):29-36. 10.1049/ip-com:20030284
ChandraKumar P, Saratchandran P, Sundararajan N: Minimal radial basis function neural networks for nonlinear channel equalisation. IEE Vision Image and Signal Processing 2000, 147(5):428-435. 10.1049/ip-vis:20000459
Chen S, Samingan AK, Mulgrew B, Hanzo L: Adaptive minimum-BER linear multiuser detection. IEEE Transactions on Signal Processing 2001, 49(6):1240-1247. 10.1109/78.923306
Dua A, Desai UB, Mallik RK: Minimum probability of error-based methods for adaptive multiuser detection in multipath DS-CDMA channels. IEEE Transactions on Wireless Communications 2004, 3(3):939-948. 10.1109/TWC.2004.827759
Hjorungnes A, Debbah M: Minimum BER FIR receiver filters for DS-CDMA systems. Proceedings of the IEEE Global Telecommunications Conference (GLOBECOM '05), December 2005, St. Louis, Mo, USA 4: 2287-2291.
Gesbert D: Robust linear MIMO receivers: a minimum error-rate approach. IEEE Transactions on Signal Processing 2003, 51(11):2863-2871. 10.1109/TSP.2003.818160
Wang XF, Lu W-S, Antoniou A: Constrained minimum-BER multiuser detection. IEEE Transactions on Signal Processing 2000, 48(10):2903-2909. 10.1109/78.869045
Gunther J, Moon T: Minimum bayes risk adaptive linear equalizers. IEEE Transactions on Signal Processing 2009, 57(12):4788-4799.
Bertsekas DP: Nonlinear Programming. 2nd edition. Athena Scientific, Belmont, Mass, USA; 1999.
Haykin S: Adaptive Filter Theory. 4th edition. Prentice Hall, New York, NY, USA; 2001.
Li VOK, Silvester JA: Performance analysis of networks with unreliable components. IEEE Transactions on Communications 1984, 32(10):1105-1110.
Steele R, Hanzo L: Mobile Radio Communications. 2nd edition. Wiley-IEEE Press, New York, NY, USA; 1999.
Failli M: Digital land mobile radio communications COST 207. European Commission; 1989.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kovacs, L., Levendovszky, J., Olah, A. et al. Approximate Minimum Bit Error Rate Equalization for Fading Channels. EURASIP J. Adv. Signal Process. 2010, 615623 (2010). https://doi.org/10.1155/2010/615623
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/615623
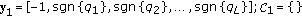 ;
;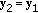 and change the sign of the component
and change the sign of the component  ;
;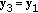 and change the sign of the component of
and change the sign of the component of 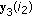 ;
; 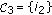 ;
; TO
TO  find the index set
find the index set  for which
for which 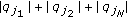 is minimal, but
is minimal, but 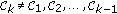 and
and  ;
; to be used in the lower bound given in (16).
to be used in the lower bound given in (16).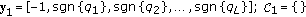 ;
;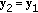 and change the sign of the component
and change the sign of the component 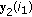 ;
; 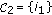 ;
;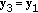 and change the sign of the component
and change the sign of the component 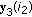 ;
; 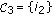 ;
;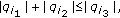 then
then  and change the sign of the components
and change the sign of the components  and
and 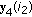 ;
; 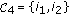 ; ELSE
; ELSE 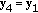 and change the sign of the component
and change the sign of the component 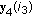 ;
; 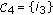 ;
; to be used in the lower bound (16).
to be used in the lower bound (16).
 versus
versus  versus for two different σ values.
versus for two different σ values.
 dominant terms in the approximation;
dominant terms in the approximation;
 versus
k
for channel
versus
k
for channel
 in the case of 3 equalizer coefficients,
in the case of 3 equalizer coefficients,
 and
and
 .
.

 and SNR = 24 dB.
and SNR = 24 dB.

 and SNR = 24 dB.
and SNR = 24 dB.

 and SNR = 24 dB.
and SNR = 24 dB.

 in the case of 3 equalizer coefficients, D = 0.
in the case of 3 equalizer coefficients, D = 0.
 in the case of 3 equalizer coefficients,
in the case of 3 equalizer coefficients,
 .
.

 in the case of 6 equalizer coefficients, D = 2.
in the case of 6 equalizer coefficients, D = 2.