- Research Article
- Open access
- Published:
Spectral Efficiency Comparison of OFDM/FBMC for Uplink Cognitive Radio Networks
EURASIP Journal on Advances in Signal Processing volume 2010, Article number: 621808 (2010)
Abstract
Cognitive radio (CR) is proposed to automatically detect and exploit unused spectrum while avoiding harmful interference to the incumbent system. In this paper, we emphasize the channel capacity comparison of a CR network using two types of multicarrier communications: conventional Orthogonal Frequency Division Multiplexing (OFDM) with Cyclic Prefix (CP) and Filter Bank based MultiCarrier (FBMC) modulations. We use a resource allocation algorithm in which subcarrier assignment and power allocation are carried out sequentially. By taking the impact of Inter-Cell Interference (ICI) resulting from timing offset into account, the maximization of total information rates is formulated under an uplink scenario with pathloss and Rayleigh fading, subject to maximum power constraint as well as mutual interference constraint between primary user (PU) and secondary user (SU). Final simulation results show that FBMC can achieve higher channel capacity than OFDM because of the low spectral leakage of its prototype filter.
1. Introduction
Cognitive Radio (CR) is a fully reconfigurable wireless system that automatically changes its communication variables in response to network and user demands. Brief overview and new development of CR technology are provided in [1–5]. The goal of the CR is to enhance spectral efficiency by overlaying a new mobile radio system on an existing one without requiring any changes to the actual licensed system, or we can say that the goal of CR is to promote the efficient use of the spectrum by sensing the existence of spectrum holes. Therefore, spectrum sensing [6, 7] is needed to ensure that secondary users would not interfere primary users. In this paper, we compare the spectral efficiency performance between OFDM and FBMC based CR networks, at the assumption of that spectrum sensing has been well implemented.
Multicarrier modulations attract a lot of attention ranging from wireline to wireless communications compared to single carrier modulation because of their capability to efficiently cope with frequency selective fading channels. In CR context, multicarrier communication has been suggested as a candidate for CR networks due to its flexibility to fill the spectrum holes [8, 9]. Much of attention in the present literature emphasizes on the use of conventional OFDM, which is able to avoid both intersymbol interference and interchannel interference making use of a suitable cyclic prefix. In [8], OFDM has been suggested as a candidate for CR systems. However, in spite of these advantages, OFDM is very sensitive to fast time variations of the radio channel and to timing offset due to imperfect synchronization. In addition, OFDM systems sacrifice data transmission rate because of the insertion of CP. The Filter Bank based MultiCarrier (FBMC) modulation [10–13], does not require CP extension and shows higher robustness to residual frequency offsets than CP-OFDM by taking advantage of the spectral containment of its modulation prototype filters. Filter bank based multicarrier system is already considered as a physical layer candidate for CR [9]. Moreover, filter banks can be used as a tool for spectrum sensing. In [14, 15], application of filter banks to spectrum sensing is proved to be more promising than FFT and Thomson's multitaper (MT) method because of its high performance and low cost.
In the literature, some system performance comparisons between OFDM and FBMC can be found in [16–23]. However, optimal resource allocation problem in multicarrier CR context with both power and mutual interference constraints is still an open topic. In [24–28], downlink power allocation problems in multicarrier based CR systems are investigated. In [25], maximization of the capacity with per subchannel power constraints is considered, but the influence of side-lobes of neighboring subcarriers is omitted. Conversely, the authors in [26] propose an optimal scheme with the interference induced to primary user, but the total power constraint is not considered. In [27], a power loading scheme to maximize the downlink capacity of the CR system under the interference and power constraints is proposed, and then according to this proposed scheme, the CR systems based on OFDM and FBMC are evaluated and compared in terms of power allocation and the system throughput in [28], in which an iterative Power Interference constraint algorithm (PI-algorithm) to iteratively allocate the subcarrier power is proposed. However, the interference induced from PU to SU is assumed to be negligible and channel pathloss is not considered.
In [23, 29], the mutual interference between PU and SU for FBMC and OFDM based CR systems are investigated, respectively. This kind of mutual interference depends on the out-of-band radiation which is determined by the power spectral density (PSD) models of multicarrier signals. In [30], intercell interferences resulting form timing offset for OFDM and FBMC based systems are firstly investigated and compared. Two tables modeling the mean interference are given. These tables give a clear model on the intercell interference, and can be used to analyze the resource allocation performance of CR networks.
In this paper, we focus on the comparison of OFDM and FBMC based CR networks in terms of the averaged spectral efficiency of the secondary system, which depends on its resource allocation strategy adopted by the secondary system. For OFDM and FBMC based non-CR systems, their capacity performances will be the same under the same system model and the same resource allocation algorithm. So whichever resource allocation algorithm is adopted in CR systems will not change the final comparison conclusion: FBMC is more efficient in spectral use than OFDM, which mainly depends on the intercell-interference level. We propose a resource allocation scheme under an uplink scenario with pathloss and Rayleigh channel, and a maximization of sum-rate is formulated with both power constraint and intercell interference constraint. The implementation of joint subcarrier assignment and power allocation needs substantial computation and therefore not considered in practical systems. Without loss of generality, our resource allocation procedure is split into two steps. First of all, SUs are assigned to the detected spectrum holes (a hole is a set of free adjacent subcarriers), which is implemented by using a proposed Averaged Capacity metric (AC-metric) and the Hungarian Algorithm (HA). This AC-metric is proved to offer a better performance than that using traditional SNR-metric. When the SUs are assigned to the spectrum holes, the second part of the procedure: power allocation, is solved by the Gradient Projection Method (GPM) [31] instead of using PI-algorithm and the Lagrangian multiplier method. GPM is an efficient mathematical tool for the convex optimization problems having linear constraints, and optimal power allocation result can be obtained with low computational complexity. The simulation results demonstrate that the spectral efficiency of FBMC based CR secondary network is close to that of the perfectly synchronized case and can achieve higher spectral efficiency than OFDM based CR network.
The rest of this paper is organized as follows. In Section 2, we give the system model and formulate our problem, wherein the mean intercell interference tables of OFDM and FBMC are introduced. In Sections 3 and 4, our proposed resource allocation algorithms for single-user and Multiuser are presented, respectively. Simulation results are given in Section 5. Finally, Section 6 concludes this paper.
2. System Model and Problem Formulation
In the context of cognitive radio system, a group of secondary users gathering and communicating with a hot spot called Secondary Base Station (SBS), make up a CR system. In the rest of this paper, we call one CR system with some secondary users and a SBS as "secondary cell".
As shown in Figure 1, an uplink scenario of CR networks consisting of one primary system with one PU and one secondary cell with one SU is graphed, where " " is the distance between the Primary Base Station (PBS) and SBS, and "
" is the distance between the Primary Base Station (PBS) and SBS, and " " and "
" and " " are the radius of primary system and secondary cell, respectively. A "
" are the radius of primary system and secondary cell, respectively. A " " MHz frequency band of "
" MHz frequency band of " " clusters with "
" clusters with " " subcarriers in each cluster is licensed to primary system. Figure 2 shows the distributions of the primary users (referred to as "
" subcarriers in each cluster is licensed to primary system. Figure 2 shows the distributions of the primary users (referred to as " ") and the spectrum holes (referred to as "
") and the spectrum holes (referred to as " ") with "
") with " " and "
" and " ". (here we have chosen the practical values of WIMAX 802.16 for the number and size of clusters).
". (here we have chosen the practical values of WIMAX 802.16 for the number and size of clusters).
Given above basic uplink scenario, we make the following assumptions for our system model.
-
(1)
The goal of this paper is the spectral efficiency comparison, so the simple scenario (Figure 1) with one primary system and one secondary cell is considered.
-
(2)
Primary system and secondary cell apply the same multicarrier modulation scheme (OFDM or FBMC).
-
(3)
SUs in the secondary cell are synchronized, and SBS can perfectly sense the free bands of the licensed system.
-
(4)
SBS has the channel knowledge of
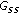 (indicated in Figure 1) and full control of its own attached SUs.
(indicated in Figure 1) and full control of its own attached SUs. -
(5)
Primary system and secondary cell are assumed to be unsynchronized, so intercell interference exists between primary system and secondary cell.
-
(6)
We consider a frequency-selective channel with flat Rayleigh fading on each subcarrier, and we assume that the channel changes slowly so that the channel gains will be constant during transmission.
In [30], OFDM/FBMC interference tables have been obtained when transmitting a single complex symbol with power that equals to " " on the
" on the  th frequency slot and the
th frequency slot and the  th time slot. The mean interference tables of CP-OFDM (
th time slot. The mean interference tables of CP-OFDM (

 ,
,  indicates one symbol period, and
indicates one symbol period, and  indicates the cyclic prefix duration (The authors in [30] have proved that the interference level will become lower with the increase of
indicates the cyclic prefix duration (The authors in [30] have proved that the interference level will become lower with the increase of  . Conversely, if we reduce
. Conversely, if we reduce  , the interference level will become higher. In our study, we have chosen the
, the interference level will become higher. In our study, we have chosen the  value of WIMAX 802.16.)) and FBMC (a filter bank with an overlapping factor "
value of WIMAX 802.16.)) and FBMC (a filter bank with an overlapping factor " " designed using the method in the projet PHYDYAS (generally, FBMCs with frequency-localized prototype filters have negligible intercell-interference because of theirs special filter configurations, therefore, the interference level almost doesn't change if we use other types of FBMCs) [32]) for an uniformly distributed timing offset
" designed using the method in the projet PHYDYAS (generally, FBMCs with frequency-localized prototype filters have negligible intercell-interference because of theirs special filter configurations, therefore, the interference level almost doesn't change if we use other types of FBMCs) [32]) for an uniformly distributed timing offset  are given in Tables 1 and 2, respectively, where only main interfering slots whose interference powers are larger than "
are given in Tables 1 and 2, respectively, where only main interfering slots whose interference powers are larger than " " are considered. We can see that the intercell interference of FBMC with "
" are considered. We can see that the intercell interference of FBMC with " " interfering slots is more localized in frequency than that of OFDM, which has "
" interfering slots is more localized in frequency than that of OFDM, which has " " interfering slots. On the other hand, the intercell interference of FBMC spreads over more time slots which depends on the length of prototype filter.
" interfering slots. On the other hand, the intercell interference of FBMC spreads over more time slots which depends on the length of prototype filter.
When we transmit a burst of independent complex symbols, the interference incurred by one subcarrier equals to the sum of the interference for all the time slots. The corresponding frequency intercell interference powers which are larger than " " for OFDM, FBMC, and the perfectly synchronized (PS) cases are given in Table 3. It can be observed that the number of subcarriers that induce harmful interference to primary user of OFDM and FBMC are "
" for OFDM, FBMC, and the perfectly synchronized (PS) cases are given in Table 3. It can be observed that the number of subcarriers that induce harmful interference to primary user of OFDM and FBMC are " " and "
" and " ", respectively.
", respectively.
As shown in Figure 2, the primary users and secondary users share adjacent frequency bands, and one spectrum hole might have one or multiple clusters, that is, one secondary user is permitted to occupy at least " " subcarriers. Nevertheless, only "
" subcarriers. Nevertheless, only " " subcarrier (FBMC) or "
" subcarrier (FBMC) or " " subcarriers (OFDM) really induces intercell interference to primary user. Intercell interferences between primary user and secondary user in OFDM and FBMC based CR networks are graphed in Figure 3. We can see that for primary user, only the eight subcarriers (OFDM) or the one subcarrier (FBMC) adjacent to secondary user suffer from the intercell interference, and the same situation for secondary user. For our following theoretical analysis, the simplified interference vectors of OFDM and FBMC are defined as (see Table 3)
" subcarriers (OFDM) really induces intercell interference to primary user. Intercell interferences between primary user and secondary user in OFDM and FBMC based CR networks are graphed in Figure 3. We can see that for primary user, only the eight subcarriers (OFDM) or the one subcarrier (FBMC) adjacent to secondary user suffer from the intercell interference, and the same situation for secondary user. For our following theoretical analysis, the simplified interference vectors of OFDM and FBMC are defined as (see Table 3)

The secondary cell wants to maximize its sum data rate by allocating power into the detected spectrum holes for its own users, this problem can be formulated as


where  is the number of secondary users,
is the number of secondary users,  is the number of spectrum holes, and
is the number of spectrum holes, and  is the number of subcarriers in the
is the number of subcarriers in the  th spectrum hole.
th spectrum hole.  is the subcarrier assignment indicator, that is,
is the subcarrier assignment indicator, that is,  if the
if the  th subcarrier in the
th subcarrier in the  th spectrum hole is allocated to SU
th spectrum hole is allocated to SU  ,
,  is the power of SU
is the power of SU  on the
on the  th subcarrier in the
th subcarrier in the  th spectrum hole,
th spectrum hole,  is the propagation channel magnitude from SU
is the propagation channel magnitude from SU  to SBS on the
to SBS on the  th subcarrier in the
th subcarrier in the  th spectrum hole,
th spectrum hole,  is the noise power, and
is the noise power, and  is the intercell interference from PU to SU on the
is the intercell interference from PU to SU on the  th subcarrier in the
th subcarrier in the  th spectrum hole.
th spectrum hole.  and
and  are the maximum user power limit and per subcarrier power limit, respectively.
are the maximum user power limit and per subcarrier power limit, respectively.  is the length of the interference vector
is the length of the interference vector  ,
,  is the power of SU
is the power of SU  on the left (right)
on the left (right)  th subcarrier in the
th subcarrier in the  th spectrum hole,
th spectrum hole,  is the propagation channel magnitude from SU
is the propagation channel magnitude from SU  to PBS on the left (right) first primary subcarrier adjacent to the
to PBS on the left (right) first primary subcarrier adjacent to the  th spectrum hole, and
th spectrum hole, and  denotes the interference threshold prescribed by the PU on the first primary subcarrier adjacent to SU.
denotes the interference threshold prescribed by the PU on the first primary subcarrier adjacent to SU.
The intercell interference from PU to SU  can be expressed in the mathematical form as follows:
can be expressed in the mathematical form as follows:

where  is the transmission power of PU located in the left (right) of the
is the transmission power of PU located in the left (right) of the  th spectrum hole, and
th spectrum hole, and  is the channel magnitude from PU located in the left (right) of the
is the channel magnitude from PU located in the left (right) of the  th spectrum hole to SBS on the
th spectrum hole to SBS on the  th subcarrier of the
th subcarrier of the  th spectrum hole. Practically, the secondary cell is not capable of obtaining the transmission power of PU and the channel information from PU to SU, but
th spectrum hole. Practically, the secondary cell is not capable of obtaining the transmission power of PU and the channel information from PU to SU, but  can be measured during spectrum sensing by SBS without need to know any prior information.
can be measured during spectrum sensing by SBS without need to know any prior information.
In (3), the third inequality constraint is related to the interference introduced by the secondary user to the primary base station. This constraint is quite difficult to manage because of the two following reasons: first of all, the threshold  has to be prescribed by the primary system. It represents the amount of interference that the primary system can accept from secondary system. Standards for multicarriers CR systems are still under study and no common definition for interference threshold is available in literature. Different thresholds corresponding to different penalties in terms of primary system capacity degradation will be used in Section 5 of this paper. Secondly, the SU needs the necessary channel knowledge. Without the information of the channel magnitude
has to be prescribed by the primary system. It represents the amount of interference that the primary system can accept from secondary system. Standards for multicarriers CR systems are still under study and no common definition for interference threshold is available in literature. Different thresholds corresponding to different penalties in terms of primary system capacity degradation will be used in Section 5 of this paper. Secondly, the SU needs the necessary channel knowledge. Without the information of the channel magnitude  between SU and PBS, the third term of the inequality constraint of (3) can't be computed. This difficulty is common to all CR systems: in order to adjust its emitted power the SU must know the amount of interference brought to the PBS. Under the hypothesis that primary and secondary systems are unsynchronized, it is hard to perfectly estimate the channel magnitude
between SU and PBS, the third term of the inequality constraint of (3) can't be computed. This difficulty is common to all CR systems: in order to adjust its emitted power the SU must know the amount of interference brought to the PBS. Under the hypothesis that primary and secondary systems are unsynchronized, it is hard to perfectly estimate the channel magnitude  . Nevertheless, a rough estimate of this magnitude can be implemented by the SU during the spectrum sensing phase. The modulus of the channel gain from PBS to SU can be estimated on the subcarriers used by primary system and, by interpolation, the channel magnitude from PBS to SU on free subcarriers can be computed. Alternatively, the information about
. Nevertheless, a rough estimate of this magnitude can be implemented by the SU during the spectrum sensing phase. The modulus of the channel gain from PBS to SU can be estimated on the subcarriers used by primary system and, by interpolation, the channel magnitude from PBS to SU on free subcarriers can be computed. Alternatively, the information about  can be carried out by a band manager that mediates between the primary and secondary users [33]. The channel magnitude of the downlink path (PBS to SU) in not equal to the reverse channel magnitude (SU to PBS) if FDD is used. However, this downlink channel magnitude can be used as a rough estimate of the uplink channel magnitude. In this case it will be necessary to add some margin on the threshold
can be carried out by a band manager that mediates between the primary and secondary users [33]. The channel magnitude of the downlink path (PBS to SU) in not equal to the reverse channel magnitude (SU to PBS) if FDD is used. However, this downlink channel magnitude can be used as a rough estimate of the uplink channel magnitude. In this case it will be necessary to add some margin on the threshold  in order to take into account the channel estimation error. Since OFDM based secondary system introduces more interference to primary users than the case of FBMC, the knowledge of
in order to take into account the channel estimation error. Since OFDM based secondary system introduces more interference to primary users than the case of FBMC, the knowledge of  is much more important for OFDM, in this case, larger margin value should be added for OFDM based CR systems.
is much more important for OFDM, in this case, larger margin value should be added for OFDM based CR systems.
3. Single-User Resource Allocation
In this section, the case with only one SU which uses the whole detected spectrum in the secondary cell is studied. The case of multiuser resource allocation will be addressed in the next section.
For the special case of single-user, the problem formulation in (3) is simplified:

where the SU is permitted to access all the " " subcarriers subject to the total power constraint, per subcarrier power constraint, as well as interference constraint.
" subcarriers subject to the total power constraint, per subcarrier power constraint, as well as interference constraint.
In mathematical optimization, the method of Lagrangian multipliers can provide a strategy for finding the maximum of (5), but the solution of extensive Lagrangian multipliers is computationally complex when " " increases. Instead, herein the Gradient Projection Method (GPM) can be applied to obtain the optimal power allocation for this simple CR uplink scenario in a low computational complexity.
" increases. Instead, herein the Gradient Projection Method (GPM) can be applied to obtain the optimal power allocation for this simple CR uplink scenario in a low computational complexity.
Rosen's gradient projection method [31] is based on projecting the search direction into the subspace tangent to the active constraints. We transform our linear constrained optimization problem into the GPM structure

where defining  is the coefficient matrix of the inequality linear constraints and
is the coefficient matrix of the inequality linear constraints and  is the coefficient vector of the inequality constraints. Making the comparison of (6) and (5), we can obtain
is the coefficient vector of the inequality constraints. Making the comparison of (6) and (5), we can obtain

Let " " be a feasible solution and suppose
" be a feasible solution and suppose  ,
,  , where
, where  and
and  . Suppose that
. Suppose that  , then the gradient projection algorithm is given as follows.
, then the gradient projection algorithm is given as follows.
-
(1)
Initialization: set
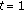 , and
, and  .
. -
(2)
Calculate the projection matrix
 , which is given by
, which is given by (8)
(8)where "
 " is the unit matrix and "
" is the unit matrix and "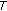 " is the transpose operator.
" is the transpose operator. -
(3)
Calculate
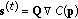 (
(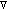 is the operator of gradient).
is the operator of gradient). -
(4)
If
 , terminate (
, terminate ( is a small threshold value).
is a small threshold value). -
(5)
Determine the maximum step size:
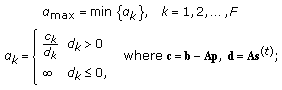 (9)
(9) -
(6)
Solve the line-search problem to find
 (10)
(10) -
(7)
Set
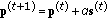 ,
, 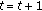 , and go to step
, and go to step  .
.
GPM is an efficient way with low computational complexity for our single-user optimization problem with linear constraints. Experimental results of one spectrum hole and multiple holes for this single-user case are given in the simulation section.
4. Multiuser Resource Allocation
In multicarrier based networks with Multiuser, assuming each free subcarrier can be used for transmission to at most one secondary user at any time, then our optimal problem in (3) is an integer programming problem, which has a high computational complexity. Generally, instead of searching an optimal solution with an unacceptable computational complexity, the combinatorial suboptimal method of subcarrier assignment and power allocation is proposed: firstly the subcarriers are assigned to the SUs and then the power is allocated to these subcarriers.
For simplicity, we solve our Multiuser resource allocation by using this two-step suboptimal algorithm. All the secondary users are firstly allocated to the available spectrum holes according to some user-selection metrics, and then power allocation is implemented. At the premise of knowing the result of the subcarrier assignment, the power allocation of Multiuser system can be virtually regarded as a single-user system and therefore the single-user power allocation algorithm GPM mentioned in last section can be utilized. So our focus is casted on the subcarrier assignment of multicarrier based CR system.
The first task of subcarrier assignment for our uplink Multiuser scenario is the bandwidth allocation. In order to guarantee the fairness for our rate adaptive optimization problem, the bandwidth allocation method in [34] is applied to assign the number of clusters to each secondary user. Afterwards, the specific subcarrier assignment is examined. In a traditional multicarrier system, the maximum SNR-metric can be applied to assign each subcarrier to the user with a high value of SNR " " (where
" (where  is the averaged power by dividing the total power limit on the number of the subcarriers). However, the SNR-metric is not always suitable in cognitive radio systems due to the mutual interference between PU and SU, especially with low interference constraint prescribed by PU.
is the averaged power by dividing the total power limit on the number of the subcarriers). However, the SNR-metric is not always suitable in cognitive radio systems due to the mutual interference between PU and SU, especially with low interference constraint prescribed by PU.
In this section, an Averaged Capacity metric (AC-metric) aiming to maximize the averaged spectral efficiency is proposed. The averaged spectral efficiency depends not only on the channel magnitude  , but also the interference threshold
, but also the interference threshold  , maximum user power limit
, maximum user power limit  , as well as the channel magnitude
, as well as the channel magnitude  . AC-metric makes a balance between all these influence factors.
. AC-metric makes a balance between all these influence factors.
It can be envisaged that different clusters in the spectrum holes suffer from different interference strengths introduced by PU. In Figure 4, four possible types of clusters in available spectrum holes are displayed, where the cluster with index " " suffers from the interferences introduced by both left PU and right PU, the cluster "
" suffers from the interferences introduced by both left PU and right PU, the cluster " " ("
" (" ") suffers from the interference introduced by only left (right) PU, and cluster "
") suffers from the interference introduced by only left (right) PU, and cluster " " does not suffer from any interference at all.
" does not suffer from any interference at all.
Considering this practical situation, the AC-metric is defined as

where  are the averaged channel capacities of the four different clusters in Figure 4, respectively,
are the averaged channel capacities of the four different clusters in Figure 4, respectively,  is the length of the interference vector
is the length of the interference vector  , "
, " " is the length of one cluster, and
" is the length of one cluster, and  is the SINR on the left (right)
is the SINR on the left (right)  th subcarrier of one cluster.
th subcarrier of one cluster.  is the power on the left (right)
is the power on the left (right)  th subcarrier of one cluster (we assume that each of the "
th subcarrier of one cluster (we assume that each of the " " subcarriers adjacent to PU introduces the same quantity of interference to PU), and which is not supposed to overpass the averaged power per subcarrier.
" subcarriers adjacent to PU introduces the same quantity of interference to PU), and which is not supposed to overpass the averaged power per subcarrier.  is the channel magnitude of SU to SBS on the left (right)
is the channel magnitude of SU to SBS on the left (right)  th subcarrier of one cluster,
th subcarrier of one cluster,  is the interference from PU to SU on the left (right)
is the interference from PU to SU on the left (right)  th subcarrier of one cluster,
th subcarrier of one cluster,  is the aggregated power on the left (right)
is the aggregated power on the left (right)  subcarriers of one cluster, and
subcarriers of one cluster, and  is the channel magnitude from SU to PBS on the left (right) first primary subcarrier adjacent to one cluster.
is the channel magnitude from SU to PBS on the left (right) first primary subcarrier adjacent to one cluster.
Assuming there are  free clusters and
free clusters and  secondary users, AC-metric can be used for calculating the averaged capacities of each SU on each available cluster. Since we know the number of clusters assigned to each secondary user using the bandwidth allocation method in [34], a
secondary users, AC-metric can be used for calculating the averaged capacities of each SU on each available cluster. Since we know the number of clusters assigned to each secondary user using the bandwidth allocation method in [34], a  AC matrix can be obtained. Our task is how to optimally assign these
AC matrix can be obtained. Our task is how to optimally assign these  clusters to the
clusters to the  secondary users, with the aim of maximizing the averaged spectral efficiency of the secondary cell. This problem equals to the search of the optimum matching of a bipartite graph, so the Hungarian algorithm introduced by Kuhn [35] is proposed to implement this cluster assignment.
secondary users, with the aim of maximizing the averaged spectral efficiency of the secondary cell. This problem equals to the search of the optimum matching of a bipartite graph, so the Hungarian algorithm introduced by Kuhn [35] is proposed to implement this cluster assignment.
Mathematically, the cluster assignment problem can be described as follows. Given the  AC cost matrix
AC cost matrix  , find the
, find the  permutation matrix
permutation matrix  so that
so that

is maximized.
For the low dimension AC matrix, the optimal permutation matrix  can be obtained efficiently by using Hungarian algorithm. The Multiuser resource allocation in CR network with multiple spectrum holes will be simulated in next section.
can be obtained efficiently by using Hungarian algorithm. The Multiuser resource allocation in CR network with multiple spectrum holes will be simulated in next section.
5. Simulations
In this section, the proposed resource allocation algorithm of OFDM and FBMC based CR networks is evaluated in terms of the averaged spectral efficiency by computer simulations in a comparable way. We will verify that FBMC based CR network achieves higher spectral efficiency than the case of OFDM.
The CR network as shown in Figure 1 with one primary system and one secondary cell is simulated for different number of users and spectrum holes. Primary and secondary users centering around PBS and SBS, respectively, are uniformly distributed within the cell range (0.1–1 km). As the increase of transmission distance, the attenuation also increases due to the propagation pathloss. The pathloss of the received signal at a distance  (km) is [36]
(km) is [36]

In order to define an interference threshold  which is predetermined by a practical licensed system (considering the absence of a standard interference threshold for CR system, we have derived it using a tolerable capacity loss for the primary system), we assume that the received primary signal in PBS always has a desired "
which is predetermined by a practical licensed system (considering the absence of a standard interference threshold for CR system, we have derived it using a tolerable capacity loss for the primary system), we assume that the received primary signal in PBS always has a desired " ". The capacity on the first primary subcarrier adjacent to SU is
". The capacity on the first primary subcarrier adjacent to SU is

where  is the primary transmission power, and
is the primary transmission power, and  is the channel magnitude from PU to PBS. The value of
is the channel magnitude from PU to PBS. The value of  can be automatically generated by defining a tolerable capacity loss coefficient
can be automatically generated by defining a tolerable capacity loss coefficient  according to
according to

Other system simulation parameters are displayed in Table 4.
During our simulation, single-user case as well as Multiuser case are considered, and meanwhile the experimental results of the perfectly synchronized (PS) case are also given for the sake of comparison with the results of OFDM and FBMC based CR networks.
5.1. Single-User Case with One and Multiple Spectrum Holes
Firstly, we investigate the single-user case with only one spectrum hole.
As shown in Figure 5, the SU who uses the  available subcarriers is surrounded by the subcarriers allocated to PU. So the SU suffers from the interference introduced by PU from both sides. With respect to the interference form SU to PU, in this paper we consider the interference strength on the first primary subcarrier adjacent to SU, and the interference threshold
available subcarriers is surrounded by the subcarriers allocated to PU. So the SU suffers from the interference introduced by PU from both sides. With respect to the interference form SU to PU, in this paper we consider the interference strength on the first primary subcarrier adjacent to SU, and the interference threshold  is determined by prescribing a tolerable capacity loss coefficient
is determined by prescribing a tolerable capacity loss coefficient  on this primary subcarrier according to (15).
on this primary subcarrier according to (15).
Given that the SBS is relatively close to PBS ( km), and in the case of one PU and one SU, there are three typical channel situations. (a) The distance from SU to SBS and PBS is larger than that of PU, in other words, PU is closer to the base stations; (b) PU and SU have almost equivalent distance to the base stations; (c) The distance from SU to the base stations is smaller than that of PU.
km), and in the case of one PU and one SU, there are three typical channel situations. (a) The distance from SU to SBS and PBS is larger than that of PU, in other words, PU is closer to the base stations; (b) PU and SU have almost equivalent distance to the base stations; (c) The distance from SU to the base stations is smaller than that of PU.
Table 5 gives three examples corresponding to above three typical channel realizations, and their power allocation results of OFDM and FBMC based systems are shown in Figure 6 with the number of subcarriers " ", the interference threshold determined according to "
", the interference threshold determined according to " ", and the power limit "
", and the power limit " mWatt". For the first channel situation (Figure 6(a)), it can be observed that the transmission power of the PU is low because the PU is close to the base stations, whereas the averaged spectral efficiencies of the SU are low because the SU is located relatively far away from the base stations. Furthermore, the gap between the averaged spectral efficiencies of OFDM and FBMC is not obvious mainly due to the low interference induced from SU to PU and slightly due to the negligible interference from PU to SU. With regard to the second and the third channel realizations (Figures 6(b) and 6(c)), the values of the SU's spectral efficiencies increase when the distance between SU and the base stations decreases, and the transmission power of the PU increases when the distance between the PU and the base stations augments. The spectral efficiency gap of OFDM and FBMC augments especially for the third channel realization because the SU is located close to the base stations, which means significant interference will be introduced to the PU. So the power allocation algorithm tries to avoid allocating the power on the subcarriers adjacent to the PU. That's why the power allocation of OFDM in Figure 6(c) is localized at the center of the spectrum hole. However, FBMC is insensitive and robust for different channel situations because of its frequency containment property.
mWatt". For the first channel situation (Figure 6(a)), it can be observed that the transmission power of the PU is low because the PU is close to the base stations, whereas the averaged spectral efficiencies of the SU are low because the SU is located relatively far away from the base stations. Furthermore, the gap between the averaged spectral efficiencies of OFDM and FBMC is not obvious mainly due to the low interference induced from SU to PU and slightly due to the negligible interference from PU to SU. With regard to the second and the third channel realizations (Figures 6(b) and 6(c)), the values of the SU's spectral efficiencies increase when the distance between SU and the base stations decreases, and the transmission power of the PU increases when the distance between the PU and the base stations augments. The spectral efficiency gap of OFDM and FBMC augments especially for the third channel realization because the SU is located close to the base stations, which means significant interference will be introduced to the PU. So the power allocation algorithm tries to avoid allocating the power on the subcarriers adjacent to the PU. That's why the power allocation of OFDM in Figure 6(c) is localized at the center of the spectrum hole. However, FBMC is insensitive and robust for different channel situations because of its frequency containment property.
Next, the spectral efficiency curves of the single-user case as a function of various system parameters are drawn in Figure 7 by averaging 200 Monte Carlo simulations. Power allocation results for the case of one spectrum hole are presented in Figures 7(a), 7(c), and 7(e), and Figures 7(b), 7(d), and 7(f) give the simulation results of the single-user case with multiple holes, where the scenario with 12 free clusters and " " subcarriers per cluster in Figure 2 is used, and the distributions of the spectrum holes are randomly generated for each channel realization.
" subcarriers per cluster in Figure 2 is used, and the distributions of the spectrum holes are randomly generated for each channel realization.
Experimental results of single-user resource allocation for one and multiple spectrum holes with  = 0. 2 km: (a) Averaged spectral efficiency versus number of subcarriers for one spectrum hole case. (b) Averaged spectral efficiency versus interference level for multiple spectrum holes case. (c) (FBMC-OFDM)/OFDM versus number of subcarriers for one spectrum hole case. (d) (FBMC-OFDM)/OFDM versus interference level for multiple spectrum holes case. (e) Averaged spectral efficiency versus total power limit for one spectrum hole case (f). Averaged spectral efficiency versus total power limit for multiple spectrum holes case.
= 0. 2 km: (a) Averaged spectral efficiency versus number of subcarriers for one spectrum hole case. (b) Averaged spectral efficiency versus interference level for multiple spectrum holes case. (c) (FBMC-OFDM)/OFDM versus number of subcarriers for one spectrum hole case. (d) (FBMC-OFDM)/OFDM versus interference level for multiple spectrum holes case. (e) Averaged spectral efficiency versus total power limit for one spectrum hole case (f). Averaged spectral efficiency versus total power limit for multiple spectrum holes case.
The effect of the number of subcarriers is illustrated in Figures 7(a) and 7(c). We can see that as the number of subcarriers decreases, FBMC obtains more spectral efficiency gain over OFDM, which indicates that FBMC is more applicable for the CR system with small size of spectrum holes. For comparison, the averaged spectral efficiencies of the multiple holes at different interference levels ( ) are given in Figures 7(b) and 7(d). As expected, OFDM shows a fast decrease of the spectral efficiency when less capacity loss is prescribed by PU, but FBMC is slightly affected by different interference levels. It can be seen that, FBMC is even much better than OFDM when low interference threshold (
) are given in Figures 7(b) and 7(d). As expected, OFDM shows a fast decrease of the spectral efficiency when less capacity loss is prescribed by PU, but FBMC is slightly affected by different interference levels. It can be seen that, FBMC is even much better than OFDM when low interference threshold ( in (3)) is prescribed, see Figure 7(b), where spectral efficiency of OFDM collapses when the interference level decreases compared to FBMC case. We can also find that the spectral efficiencies of one spectrum hole case fit in well with the case of the multiple holes under the same simulation condition (indicated by the dashed lines in Figures 7(a) and 7(b)). Figures 7(c) and 7(d) show the ratio of the spectral efficiency gain of FBMC compared to the spectral efficiency of OFDM. When "
in (3)) is prescribed, see Figure 7(b), where spectral efficiency of OFDM collapses when the interference level decreases compared to FBMC case. We can also find that the spectral efficiencies of one spectrum hole case fit in well with the case of the multiple holes under the same simulation condition (indicated by the dashed lines in Figures 7(a) and 7(b)). Figures 7(c) and 7(d) show the ratio of the spectral efficiency gain of FBMC compared to the spectral efficiency of OFDM. When " ", FBMC can achieve almost
", FBMC can achieve almost  spectral efficiency gain over OFDM. The performance of OFDM in the case of the multiple holes is found to behave a little better than the case of one spectrum hole with "
spectral efficiency gain over OFDM. The performance of OFDM in the case of the multiple holes is found to behave a little better than the case of one spectrum hole with " " subcarriers, which can be explained by the fact each spectrum hole may have two or more than two clusters. Finally, the averaged spectral efficiencies as a function of the total power level
" subcarriers, which can be explained by the fact each spectrum hole may have two or more than two clusters. Finally, the averaged spectral efficiencies as a function of the total power level  are given in Figures 7(e) and 7(f), and the spectral efficiencies increase with the augmentation of the averaged power per subcarrier
are given in Figures 7(e) and 7(f), and the spectral efficiencies increase with the augmentation of the averaged power per subcarrier  (
( ). Besides, it can be noted that the performance of FBMC approaches the performance of the perfectly synchronized case.
). Besides, it can be noted that the performance of FBMC approaches the performance of the perfectly synchronized case.
5.2. Multiuser Case with Multiple Spectrum Holes
Without loss of generality for the proposed resource allocation algorithm, the case with multiple PUs and multiple SUs is simulated. In addition, the performance comparison of the SNR-metric and the AC-metric for channel assignment is investigated.
Since 36 clusters (seventy five percent of the total 48 clusters) are allocated to PUs, we assume that these 36 licensed clusters are occupied by 36 uniformly distributed PUs. The rest 12 clusters are permitted to access by the SUs, each of which can use at least one cluster. The cluster assignment is implemented by the traditional SNR-metric and the proposed AC metric, respectively.
Figure 8 shows the averaged spectral efficiencies of the "6 SUs" and "12 SUs" cases versus different system parameters. The spectral efficiency curves of the Multiuser case versus the interference level and the maximum user power plotted in Figures 8(a)–8(d) match the case of the single-user, which once again proves the advantage of FBMC. At the same time, we can see that the achieved spectral efficiency of the OFDM based CR system by applying the AC-metric always outperforms the SNR-metric, but there is a slight difference by applying these two metrics for the FBMC based system. This implies that the traditional subcarrier assignment methods in wireless communication system can be used in FBMC based CR network, which reduces the CR system complexity. Nevertheless, some modified methods like AC-metric with computational complexity have to be investigated for OFDM based CR network due to its seriously additional interference. In view of the fact that the distance  between SBS and PBS can be random because of the flexibility of cognitive radio, so the impact of
between SBS and PBS can be random because of the flexibility of cognitive radio, so the impact of  on spectral efficiency is investigated and shown in Figures 8(e) and 8(f). We can observe that as the distance increases, all the performance curves of FBMC and OFDM tend to merge. The reason is that there exists little interference between the primary system and the secondary cell when they are far away from each other.
on spectral efficiency is investigated and shown in Figures 8(e) and 8(f). We can observe that as the distance increases, all the performance curves of FBMC and OFDM tend to merge. The reason is that there exists little interference between the primary system and the secondary cell when they are far away from each other.
Experimental results of Multiuser resource allocation for multiple spectrum holes with  : (a) Averaged spectral efficiency versus interference level for 6 SUs. (b) Averaged spectral efficiency versus interference level for 12 SUs. (c) Averaged spectral efficiency versus maximum user power limit for 6 SUs. (d) Averaged spectral efficiency versus maximum user power limit for 12 SUs. (e) Averaged spectral efficiency versus distance between SBS and PBS for 6 SUs. (f) Averaged spectral efficiency versus distance between SBS and PBS for 12 SUs.
: (a) Averaged spectral efficiency versus interference level for 6 SUs. (b) Averaged spectral efficiency versus interference level for 12 SUs. (c) Averaged spectral efficiency versus maximum user power limit for 6 SUs. (d) Averaged spectral efficiency versus maximum user power limit for 12 SUs. (e) Averaged spectral efficiency versus distance between SBS and PBS for 6 SUs. (f) Averaged spectral efficiency versus distance between SBS and PBS for 12 SUs.
In our scenario, all the numerical results have been simulated under the assumption: the primary system and the secondary cell are regarded as mutually unsynchronized, the Rayleigh channel with pathloss is considered, and the practical system parameters and constraints are used for our simulation, all of these hypotheses are close to a realistic CR network. Based on this kind of system model, final simulation results of different cases indicate that FBMC based CR network can achieve higher spectral efficiency than the case of OFDM. Besides, the inserted cyclic prefix (not considered in this paper) in OFDM based CR system lowers the total system spectral efficiency. As a consequence, the FBMC access technique providing better system performance is practical and therefore recommended in the future wireless communication CR networks.
6. Conclusion
The objective of this paper is to compare the spectral efficiency performance of OFDM and FBMC based on a realistic uplink CR network. A resource allocation algorithm with the considerations of power constraint and interference constraint is proposed for evaluating the averaged spectral efficiency. Instead of using the interference due to the out-of-band radiation of the power spectral density, intercell interferences resulting from timing offset in OFDM and FBMC based networks are considered in our proposed algorithm. Scenario cases with different number of users and spectrum holes are investigated. Like most of the traditional suboptimal resource allocation algorithms, our problem is separated into two steps: subcarrier assignment and power allocation. In the case of Multiuser, traditional SNR-metric for subcarrier assignment is not always suitable for CR network because of the existence of mutual interference between PU and SU, thus we propose an enhanced AC-metric for subcarrier assignment, which turns out to be more efficient than SNR-metric. Another contribution of this paper is that gradient projection method is used for solving the power allocation problem, and optimal solution can be derived with low complexity. Final simulation results demonstrate that in our scenario FBMC offers higher spectral efficiency and is more applicable for the CR network with small size of spectrum holes than OFDM. Furthermore, the performance of FBMC is close to that of the perfectly synchronized case because of its frequency localization and therefore simplified resource allocation schemes could be sufficient for FBMC based CR network in practice to reach the performance close to the perfectly synchronized case. As a result, we conclude that FBMC has practical value and is a potential candidate for physical layer data communication of future CR networks.
Our future work will focus on the study of a scenario with multiple unsynchronized secondary cells, where game theory can be used for solving the global resource allocation problem.
References
Haykin S: Cognitive radio: brain-empowered wireless communications. IEEE Journal on Selected Areas in Communications 2005, 23(2):201-220.
Akyildiz IF, Lee W-Y, Vuran MC, Mohanty S: NeXt generation/dynamic spectrum access/cognitive radio wireless networks: a survey. Computer Networks 2006, 50(13):2127-2159. 10.1016/j.comnet.2006.05.001
Buddhikot MM: Understanding dynamic spectrum access: models, taxonomy and challenges. Proceedings of the 2nd IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN '07), April 2007 649-663.
Zhao Y, Mao S, Neel JO, Reed JH: Performance evaluation of cognitive radios: metrics, utility functions, and methodology. Proceedings of the IEEE 2009, 97(4):642-658.
Stevenson CR, Chouinard G, Lei Z, Hu W: IEEE 802.22: the first cognitive radio wireless regional area network standard. IEEE Standards in Communications and Networking 1976, 47(1):130-138.
Yucek T, Arslan H: A survey of spectrum sensing algorithms for cognitive radio applications. IEEE Communications Surveys and Tutorials 2009, 11(1):116-130.
Haykin S, Thomson DJ, Reed JH: Spectrum sensing for cognitive radio. Proceedings of the IEEE 2009, 97(5):849-877.
Weiss TA, Jondral FK: Spectrum pooling: an innovative strategy for the enhancement of spectrum efficiency. IEEE Communications Magazine 2004, 42(3):S8-S14.
Amini P, Kempter P, Chen RR, Lin L: Filter bank multitone: a physical layer candidate for cognitive radios. Proceeding of the SDR Forum technical Conference, November 2005 14-18.
Le Floch B, Alard M, Berrou C: Coded orthogonal frequency division multiplex. Proceedings of the IEEE 1995, 83: 982-996. 10.1109/5.387096
Bellanger MG: Specification and design of a prototype filter for filter bank based multicarrier transmission. Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '01), 2001 4: 2417-2420.
Siohan P, Siclet C, Lacaille N: Analysis and design of OFDM/OQAM systems based on filterbank theory. IEEE Transactions on Signal Processing 2002, 50(5):1170-1183. 10.1109/78.995073
Bellanger M: Filter banks and OFDM-OQAM for high throughput wireless LAN. Proceedings of the 3rd International Symposium on Communications, Control, and Signal Processing (ISCCSP '08), March 2008, St. Julians, Malta 758-761.
Farhang-Boroujeny B, Kempter R: Multicarrier communication techniques for spectrum sensing and communication in cognitive radios. IEEE Communications Magazine 2008, 46(4):80-85.
Farhang-Boroujeny B: Filter bank spectrum sensing for cognitive radios. IEEE Transactions on Signal Processing 2008, 56(5):1801-1811.
Rhee W, Chuang JC, Cimini LJ Jr.: Performance comparison of OFDM and multitone with polyphase filter bank for wireless communications. Proceedings of the 48th IEEE Vehicular Technology Conference (VTC '98), May 1998, Ottawa, Canada 2: 768-772.
Lacroix D, Goudard N, Alard M: OFDM with guard interval versus OFDM/OffsetQAM for high data rate UMTS downlink transmission. Proceedings of IEEE Vehicular Technology Conference (VTC '01), 2001 4: 2682-2686.
Lee CS, Yoo KY: Polyphase filter-based OFDM transmission system. Proceedings of IEEE Vehicular Technology Conference (VTC '04), September 2004 1: 525-528.
Waldhauser DS, Baltar LG, Nossek JA: Comparison of filter bank based multicarrier systems with OFDM. Proceedings of IEEE Asia-Pacific Conference on Circuits and Systems (APCCAS '06), December 2006 976-979.
Ihalainen T, Stitz TH, Viholainen A, Renfors M: Performance comparison of LDPC-coded FBMC and CP-OFDM in beyond 3G context. Proceedings of IEEE International Symposium on Circuits and Systems (ISCAS '06), 2006 2049-2052.
Baltar LG, Waldhauser DS, Nossek JA: Out-of-band radiation in multicarrier systems: a comparison. In Multi-Carrier Spread Spectrum 2007, Lecture Notes in Electrical Engineering. Volume 1. Springer, Berlin, Germany; 2007:107-116. 10.1007/978-1-4020-6129-5_11
Du J, Signell S: Comparison of CP-OFDM and OFDM/OQAM in doubly dispersive channels. Proceedings of Future Generation Communication and Networking (FGCN '07), December 2007 2: 207-211.
Zhang H, Le Ruyet D, Terré M: Spectral efficiency comparison between OFDM/OQAM- and OFDM-based CR networks. Wireless Communications and Mobile Computing 2009, 9(11):1487-1501. 10.1002/wcm.704
Qin T, Leung C: Fair adaptive resource allocation for multiuser OFDM cognitive radio systems. Proceedings of the 2nd International Conference on Communications and Networking in China (CHINACOM '07), August 2007, Shanghai, China 115-119.
Wang P, Zhao M, Xiao L, Zhou S, Wang J: Power allocation in OFDM-based cognitive radio systems. Proceedings of the 50th Annual IEEE Global Telecommunications Conference (GLOBECOM '07), November 2007, Washington, DC, USA 4061-4065.
Bansal G, Hossain MJ, Bhargava VK: Adaptive power loading for OFDM-based cognitive radio systems. Proceedings of IEEE International Conference on Communications (ICC '07), June 2007 5137-5142.
Shaat M, Bader F: Power allocation with interference constraint in multicarrier based cognitive radio systems. In Multi-Carrier Systems and Solutions. Chapter 4: Adaptive Transmission. Edited by: Plass S, Dammann A, Kaiser S, Fazel K. Springer, Berlin, Germany; 2009.
Shaat M, Bader F: Power allocation and throughput comparison in OFDM and FBMC based cognitive radio. Proceedings of the 22nd Meeting of the Wireless World Research Forum (WWRF '09), May 2009, Paris, France
Weiss T, Hillenbrand J, Krohn A, Jondral FK: Mutual interference in OFDM-based spectrum pooling systems. Proceedings of IEEE Vehicular Technology Conference (VTC '04), May 2004 4: 1873-1877.
Medjahdi Y, Terré M, Le Ruyet D, Roviras D, Nossek JA, Baltar L: Inter-cell interference analysis for OFDM/FBMC systems. Proceedings of the 10th IEEE Workshop on Signal Processing Advances in Wireless Communications (SPAWC '09), June 2009, Perugia, Italy 598-602.
Barzaraa MS, Sherali HD, Shetty CM: Nonlinear Programming: Theory and Algorithms. 2nd edition. John Wiley & Sons, New York, NY, USA; 1993.
PHYDYAS-physical layer for dynamic spectrum access and cognitive radio http://www.ict-phydyas.org/
Peha JM: Approaches to spectrum sharing. IEEE Communications Magazine 2005, 43(2):10-12.
Lengoumbi C, Godlewski P, Martins P: An efficient subcarrier assignment algorithm for downlink OFDMA. Proceedings of IEEE Vehicular Technology Conference (VTC '06), September 2006 1258-1262.
Kuhn HW: Variants of the hungarian method for assignment problems. Naval Research Logistics Quarterly 1956, 3(4):253-258. 10.1002/nav.3800030404
Draft IEEE 802.16 m Evaluation Methodology Document C80216 m-07-080r2
Acknowledgment
This work was supported in part by the European Commission under Project PHYDYAS (FP7-ICT-2007-1-211887)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhang, H., Le Ruyet, D., Roviras, D. et al. Spectral Efficiency Comparison of OFDM/FBMC for Uplink Cognitive Radio Networks. EURASIP J. Adv. Signal Process. 2010, 621808 (2010). https://doi.org/10.1155/2010/621808
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/621808


 " and
" and  .
.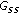 (indicated in Figure
(indicated in Figure 
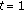 , and
, and  .
. , which is given by
, which is given by
 " is the unit matrix and "
" is the unit matrix and "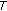 " is the transpose operator.
" is the transpose operator.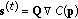 (
(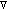 is the operator of gradient).
is the operator of gradient). , terminate (
, terminate ( is a small threshold value).
is a small threshold value).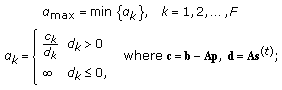

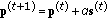 ,
, 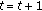 , and go to step
, and go to step  .
.

 subcarriers in one spectrum hole.
subcarriers in one spectrum hole.

 ,
,
 ,
,
 km, and
km, and
 mWatt: (a)
mWatt: (a)
 (b)
(b)
 (c)
(c)
 .
.

